最大频繁模式挖掘算法的改进

2019-05-27王利军

韶关学院学报 2019年3期

王利军

（安徽经济管理学院信息工程系，安徽合肥 230031）

FPMax算法［1］在数据挖掘过程主要包括几个步骤：（1）第一次对事务数据库D进行扫描，并将数据库中事务数据信息读取出来并存储到内存中，对事务数据信息包含的数据项进行频度统计和排序，对每一个事务中事务项按照从高到低的顺序排序形成有序事务，根据最小支持度进行删除相应的事务项，符合要求的事务项按照从高到低的顺序从而生成项头表L；（2）第二次对数据库D进行扫描来构建FP-tree结构；（3）根据FP-tree结构进行最大频繁模式挖掘则.笔者对FPMax算法的数据挖掘过程进行改进，以提高挖掘的效率.最大频繁项集中包含了所有频繁项集的频繁信息，且最大频繁项集的规模要小几个数量级.所以在数据集中含有较长的频繁模式时，挖掘最大频繁项集是非常有效的挖掘手段.

1 相关理论与性质

1.1 频繁项集和最大频繁项集

设 I={i1，i2，...，im}为项（Item）的集合，事务数据库 D={T1，T2，...，Tn}，i∈［1，n］，事务 Ti是由 I中的若干项组成.设S是由若干项组成的一个集合，简称项集（Itemset），包含k个项的项集称为k-项集.项集S的支持度计数是指D中包含项集S的事务数量，支持度sup（S）=（项集S的支持度计数/D的总事务数量）×100%.

定义1 频繁项集：若S的支持度sup（S）≥给定的最小支持度min_sup，则称S为频繁项集（Frequent Itemset）［2］.

定义2 最大频繁项集：若一个集合S2中的每一个元素都在集合S1中，且集合S1中可能包含S2中没有的元素，则集合S1就是S2的一个超集［3］.S1是S2的超集，则S2是S1的真子集，如果频繁项集L的所有超集都是非频繁项集，那么称L为最大频繁项集或称最大频繁模式，记为MFI（Maximal Frequent Itemset）.频繁项集是最大频繁项集的子集.

性质1 若整个FP-tree结构T{a}为单支树即只包含一个分支，a为后缀项集，则可以直接设置后缀项集a的支持度计数=T{a}对应的项头表L{a}最后一项的支持度计数，将后缀项集与项头表L{a}的所有项进行并集操作即可得到最大频繁项集，无需对每一个事务项进行挖掘.

证若设置最小支持度计数为2，在挖掘项头表中的事务项G时，发现G在初始FP-tree结构T{φ}出现了两个分支＜A，C，G∶1＞和＜A，C，E，G∶4＞，G 为后缀，则它的前缀路径为＜A，C∶1＞和＜A，C，E∶4＞，形成 G的条件模式基{{A，C∶1}，{A，C，E∶4}}，创建 G 的条件子树 FP-tree 结构 T{G}；根据 FP-growth 算法挖掘的频繁项集为频繁 2 项集{A∶5，G∶5}，{C∶5，G∶5}，{E∶4，G∶4}，合并频繁 2 项集得到频繁 3 项集为{A∶5，G∶5，C∶5}，{A∶5，G∶4，E∶4}，{C∶5，G∶4，E∶4}，合并频繁 3 项集得到频繁 4 项集为{A∶5，C∶5，G∶4，E∶4}为最大频繁项集.

根据性质1可获得后缀项集{G}并设置支持度计数为项头表L{G}中的E的支持度计数得{G∶4}，再读取项头表 L{G}所有项得到项集{A∶5，C∶5，E∶4}，将两者进行并集得到{A∶5，C∶5，G∶4，E∶4}，得证.

引理1a为后缀项集，若项头表L{a}中的某个事务项i在FP-tree树结构T{a}中只存在一条路径即单路径（通过该事务项i的起始指针链在T{a}中只找到一个同名节点），则该事务项i的条件子树T{a∪i}必为单支树.

引理2若项头表L{a}中的某个事务项i在FP-tree树结构T{a}中为单路径，若能提前获得事务项i的条件子树T{a∪i}对应的项头表L{a∪i}中事务项和支持度计数，则无需创建条件子树T{a∪i}，后缀项集设置为a∪i，支持度为项头表L{a∪i}中最小的支持度计数，就可以根据性质1获得最大频繁项集.

引理1及引理2的证明过程较简单，笔者不再一一列举.

1.2 FPMax算法

最大频繁项集涵盖了所有的频繁项集，并且在数量上远小于频繁项集数量，并且在某些领域只需要最大频繁项集，故挖掘最大频繁项集对数据挖掘具有重要价值.目前，具有代表性的最大频繁项集挖掘算法有 FPMax 算法［4］、MaxMiner 算法［5］、MAFIA 算法［6］等.

FPMax算法是FP-growth算法［7］的一种扩展方案，该算法是基于FP-tree树结构采用深度优先算法来挖掘最大频繁项集的，它依旧使用FP-tree树结构来压缩存储事务数据库中与频繁项集的相关信息，最终采用MFI-tree树结构［8］来保存最大频繁项集，达到快速挖掘最大频繁项集的目的.但FPMax算法须对每一个挖掘项目进行条件子树的创建，当存在大量长模式和强模式时，需要创建大量的条件模式子树，消耗了巨大的时空资源.在创建条件模式子树时，需要通过项头表中的事务项的节点链来找到相同元素的节点，获得前缀路径来确定事务项对应的条件模式基，这种遍历查找也会耗费大量的时间.

1.3 DFP-数组

经典的FP-growth方法挖掘频繁模式是通过项头表中的相同元素链表的起始指针进行查找每一个事务项相同元素的位置后再回溯得到项头表中每个项的条件模式基再形成条件树，采用递归的方式进行挖掘的.回溯虽然不是全遍历树结构，仍需要耗费大量的系统资源，为了减少回溯FP-tree树结构次数提高挖掘效率，在这里提出了DFP-数组结构，若项头表中项的个数为M，则相应的DFP-数组为一个规模为M×（M-1）/2二维结构，该结构的总行数为M-1，第一行的元素个数为1，逐行元素个数递增1，直到最后一行的元素个数为M-1，每一个元素的默认值为0.在建立树结构时对DFP-数组中的相应的元素值进行修改，如按项头表中项支持度计数从高到低排完序的事务{A2，A1，A5}，则只需要将元素［A2，A1］，［A2，A5］，［A1，A5］对应的元素位置全部加1，直到所有排完序的事务读取完后，DFP-数组即可以完成，该DFP-数组存储的数值是项头表中的每一个项的2-项集支持度计数，项头表中事务项对应的条件模式基的频繁项集可以直接读取DFP-数组的相关行，可为下一轮创建条件子树使用.

2 算法改进

为了更快的挖掘最大频繁项集，笔者对FPMax算法进行了一些改进，为区别FPMax算法，将改进的算法命名为DFP-growth-Max算法.以实例的方式进行阐述内容，设置最小支持度计数为2，第一次对事务数据库D（见表1），进行扫描时，发现只有7个事务项为频繁项集分别为A，B，C，D，E，F，G，形成项头表.

2.1 改进一：DFP-tree建树方法和DFP-数组技术

当数据量变得很大时，构建FP-tree结构过程中遍历比较子节点需要耗费大量的系统资源，为了减少构建过程遍历比较的次数，提出一种时间效率优先的DFP-tree构建方法，该方法可以通过增加节点信息量，即为每一个节点再增加一个数据域CNB（存储该节点的子节点信息），再创建一个指针数据域CNA（存储子节点邻接表最后一个链表节点的地址），为提高后期的数据挖掘效率，在创建DFP-tree的同时生成DFP-数组，DFP-tree具体构建方法描述有几个步骤.

表1 事务数据库D

根据项头表L获得符合最小支持度计数的事务项的个数M，创建一个规模为M×（M-1）/2的DFP-数组，创建根节点null并为它生成数据域CNB，为根节点null构造一个M位的二进制数S（每一个二进制位默认值为0），将S存储到根节点null的数据域CNB中，根节点null节点为当前节点，如果当前节点不是根节点则支持度计数增1.为了方便创建DFP-tree结构创建一个指针数据域CNA，指针数据域CNA指向当前节点即根节点null，所有的事务已在第二步过程中对数据项进行了删除和排序，例如将第一个事务中的第一个事务项对应到DFP-tree上时，构造一个与当前节点相同位数的二进制数T（每一个二进制位默认值为0），然后读取这个事务项在项头表L中的位置为i，将T的第i位二进制位修改为1，然后将S 和 T 进行位与运算（位与运算规则如下：0﹠0=0，1﹠0=0，0﹠1=0，1﹠1=1）.

若得到的结果为0，说明当前节点即根节点null的子节点中没有当前事务项，则不需要遍历从而节省了时间，则可以立即在指针数据域CNA指向的链表节点后插入一个新节点，新节点名为事务项名，新节点的计数count设置为1，再将S和T进行位或运算（位或运算规则如下：0|0=0，1|0=1，0|1=1，1|1=1），将位或运算的结果更新当前节点即根结点null的数据域CNB的值，同时给这个新节点的CNB域中存入一个（M-i）位的二进制数W（每一个二进制位默认值为0），将指针数据域CNA的指向地址更改为新节点的地址，使这个新节点成为当前节点（方便插入下一个事务项），还原二进制数T的每一位为0.

若S和T进行位与运算的结果不为0，说明当前节点即根节点null的子节点中存在当前事务项，遍历查找这个相同的节点，并将该节点的计数count增加1，当前节点的CNB域保持不变，将指针数据域CNA的指向地址更改为这个子节点的地址（方便插入下一个事务项），使其成为当前节点，还原二进制数T的每一位为0.

第一个事务中的第一个事务项插入完毕后，判断是否有第二个事务项，如果有则读取指针数据域CNA指向的当前节点的CNB中的值存入S，继续运用上述形成节点的方法来构建DFP-tree，当一个事务的所有事务项都插入到树中后，指针数据域CNA的指向地址更改为根节点null继续插入下一个事务.

构建DFP-tree过程与经典的构建FP-tree过程的相比较，经典的构建FP-tree过程在插入新的节点时都需要遍历子节点集才能确定是否有跟待插入的节点相同的子节点，构建DFP-tree过程主要优势在于通过位与运算来判定待插入的事务项是否在当前节点的子节点集中，如果位与运算结果为0，则不需要遍历当前节点的子节点集就可以直接插入新节点，避免了许多无用的遍历查找过程，提高了创建DFP-tree结构的效率，特别在事务数据库为低关联聚集度［9］时，若构建树结构分枝较多，利用DFP-tree创建的方法可避免大量的无用遍历操作，节省创建树结构的时间.基于表1的事务数据库D生成的DFP-tree结构T{φ}见图1，对应的DFP-数组见图2.

图 1 DFP-tree结构 T{φ}

图 2 DFP-数组 A{φ}

从空间角度来看，构建DFP-tree完成后，节点中的CNB域中二进制信息就失去了利用价值，程序可以采用相应的方法立即释放节点的CNB的空间，从而达到减少空间的浪费.DFP-tree建树方法在建树过程中会增加对内存的使用，但建树完成后释放CNB域的空间后，内存的使用情况与FP-tree结构占用的内容空间一样.

2.2 改进二：DFP-growth-Max算法

FPMax算法对于一个条件FP-tree结构Tx的项头表Lx中每一个项i，都会构建一个新的条件FP-tree结构TxU{i}，这样需要对Tx遍历两次，这样需要耗费大量的时间，第一次遍历是为了获得该项的条件模式基中所有频繁项并按照支持度计数降序排序，形成条件FP-tree结构TxU{i}的项头表LxU{i}；第二次遍历是为了构建条件FP-tree结构TxU{i}.如果可以将上述两次遍历变成一次遍历，即可大大提高建树的效率.

改进方案描述：若在建立DFP-tree结构Tx的同时建立一个对应DFP-数组Ax，通过这个DFP-数组Ax即可轻松得到Tx的项头表中每一个项i的条件模式基中的所有频繁项，对这些频繁项按照支持度计数降序排序即可得到条件DFP-tree结构TxU{i}的项头表LxU{i}，从而减少对条件DFP-tree结构Tx的遍历次数，提高挖掘效率；并且在构建子条件DFP-tree结构TxU{i}时仍然采用DFP-tree方法，进一步加快生成子条件DFP-tree结构TxU{i}的效率.

基于DFP-tree方法和DFP-数组对FPMax算法进行了改进，可以大大提高挖掘效率，DFP-growth-Max算法的伪代码如下：

初始化：最大的频繁项集集合MaxFI=Ø，后缀项集p=Ø

调用函数：DFP-growth-Max（p，T{φ}，Minsup） //实际参数 T{φ}为初始 DFP-tree，实际参数 Minsup 为最小支持度计数

Procedure DFP-growth-Max（a，T{a}，min_sup） //定义 DFP-growth 函数

输入：形式参数1为a为后缀项集

形式参数2为a的条件DFP-tree结构T{a}

形式参数3为最小支持度计数min_sup

输出：最大的频繁项集集合max_fi

If整个T{a}为单支树 then{

设置后缀项集a的支持度计数=D{a}last的支持度计数；//D{a}last是项头表L{a}最后一项

形成候选最大频繁项集a∪L{a}ALL； //L{a}ALL为T{a}对应的项头表L{a}所有频繁项集及支持度计数

If a∪L{a}ALL不是max_fi中最大频繁项目集的子集 then{将a∪L{a}ALL加入max_fi；} }

Else for T{a}的项头表L{a}中的每个事务项D{a}i{ //从L{a}的最后一个事务项开始

If D{a}i在T{a}中为单路径 then{

读取DFP-数组A{a}中事务项D{a}i对应行中的频繁项集及支持度计数H{a}i；

后缀项集a=a∪D{a}i，支持度=H{a}i中最小的支持度计数；

形成候选最大频繁项集a∪H{a}i；

If a∪H{a}i不是max_fi中最大频繁项目集的子集 then{

将 a∪H{a}i加入 max_fi；} } }

Else{后缀项集a=a∪D{a}i；

从A{a}构造D{a}i的条件子DFP-tree结构T{a}i的项头表L{a}i；

采用DFP-tree方法构造D{a}i的条件DFP-tree结构T{a}i和DFP-数组结构A{a}i；

递归调用 DFP-growth-Max（a,T{a}i,minsup）； } }.

事务项A为项头表中的第一项，它的条件模式基为空，所以不用挖掘，若想得到某一事务项Ij的条件模式基的频繁项，则可以直接读取DFP-数组中与事务项Ij相应的行，剔除小于最小支持度的项，即可得到条件模式基的频繁项集和其相对应的支持度计数，见表2.

T{φ}包含多个分支，则必须从项头表的最后一项开始挖掘，项头表中的事务项在DFP-tree结构T{φ}中的路径状态存在两种情况：

若事务项i在DFP-tree结构T{φ}中为单路径（可通过项头每个事务项的起始指针从DFP-tree结构T{φ}中查找，若找到第一个节点后没有相同元素节点，则为单路径），无需创建条件DFP-tree子结构，将后缀项集与事务项i取并集，再将合并的后缀项集的支持度计数设置为该事务项i的在DFP-数组中对应行中的频繁项集中最小的支持度计数，再直接读取DFP-数组A{φ}获取该事务项的条件模式基的频繁项集和支持度计数，并直接与后缀项取集并集，即可得到最大频繁项集，无需遍历创建条件子树浪费时间和空间，大大提高挖掘效率，虽然DFP-数组的存在会占用一定的内存空间，但减少的条件子树空间也是非常可观的，所以空间的使用情况变化不大，如本例中的事务项 F、B、C，则直接获得最大频繁项集{A∶2，C∶2，E∶2，B∶2，F∶2}，{A∶2，C∶2，E∶2，B∶2}，{A∶8，C∶8}.

若事务项在条件DFP-tree结构T{φ}为多路径，不能直接挖掘出频繁项集，如事务项D在DFP-tree结构 T{φ}出现了两个分支＜A，C，E，G，D：1＞和＜A，C，D∶1＞，设置后缀路径为＜D＞，则它的前缀路径为＜A，C，E，G∶1＞和＜A，C∶1＞，形成 D 的条件模式基{{A，C，E，G∶1}，{A，C∶1}}，D 的条件模式基中的频繁项可以直接通过DFP-数组A{φ}的第5行读取得到{A∶2，C∶2}，并根据它们的计数值按高到低进行排序形成子树的项头表L{D}，避免获取条件模式基中的信息浪费时间，提高挖掘效率，采用DFP-tree方法创建D的条件子树DFP-tree结构T{D}和DFP-数组A{D}（见图3），若项头表L{D}中的事务项依旧存在多路径，则形成相应的后缀项，并可以直接读取DFP-数组A{D}中的相关行数据，为下一轮创建条件子树做好准备.

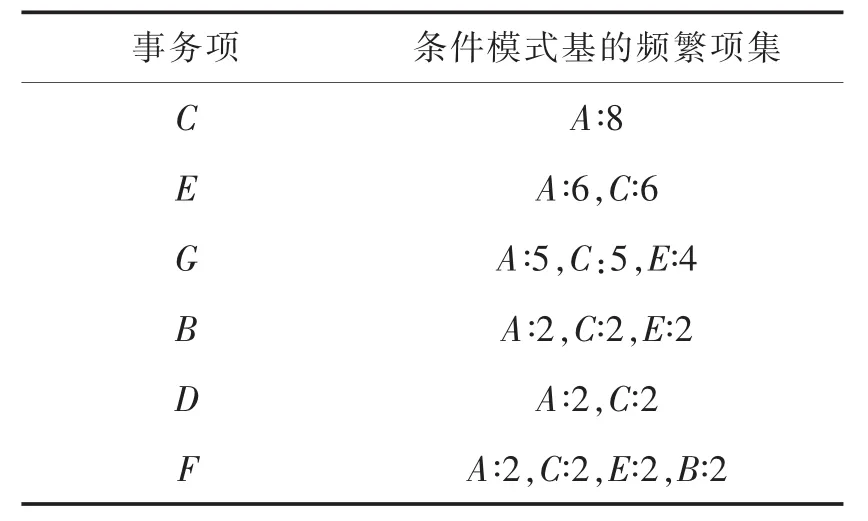
表2 事务项与对应的条件模式基的频繁项集

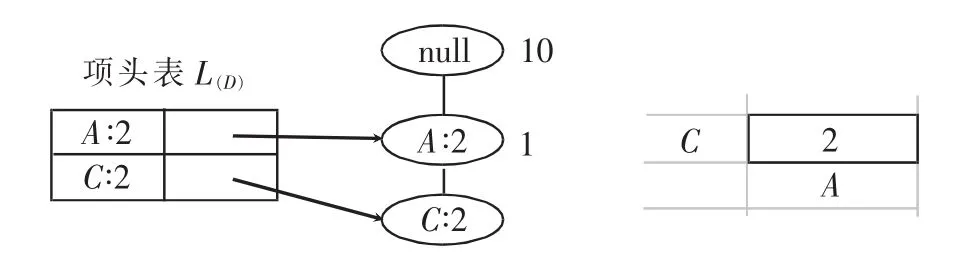
图3 D的条件子树DFP-tree结构T{D}和DFP-数组A{D}

D的条件子树DFP-tree结构T{D}只有一个分支，此时的后缀路径为＜D＞，后缀项集的支持度计数设置为项头表L{D}最后一项C的支持度计数，将后缀项集与项头表L{D}的所有项集取并集即可直接得到最大频繁项集{A∶2，C∶2，D∶2}，无需对项头表中的每一个事务项进行挖掘，更无需再递归调用DFP-tree方法创建子树和子DFP-数组.

项头表中的事务项在DFP-tree结构中是单路径还是多路径，可借助DFP-数组快速挖掘最大频繁模式，并且上述理论仍适合条件子树中.

同理获得 G 在 DFP-tree 结构 T{φ}出现了两个分支＜ A，C， G∶1＞和＜ A，C，E，G∶4＞，G 为后缀，根据上述原理快速创建 G 的条件子树 DFP-tree 结构 T{φ}，得到最大频繁项集{A∶5，C∶5，E，G∶4}；依据上述方法获得 E 的最大频繁项集{A∶6，C∶6，E∶6}.

基于DFP-tree方法和DFP-数组的挖掘算法DFP-growth-Max用来挖掘最大频繁项集，最终转化成挖掘单支树和单路径即可获得最大频繁项集.

2.3 算法性能测试

采用FPMax和DFP-growth-Max两种不同的算法对相同的数据集进行挖掘最大频繁模式，DFP-growth-Max算法对空间的影响并不是很大，所以实验主要是验证算法挖掘的时间效率，通过图表的方式展示结果，分析比较图表中信息来验证基于DFP-tree建树方法和DFP-数组技术的DFP-growth-Max算法的优越性.

实验使用的3个标准数据集是从fimi.ua.ac.be/data/的网页上下载获得的，分别是T10I4D100K、mushroom和Accidents，T10I4D100K包含100 000个事务，999个事务项，平均事务长度为10，实验选择支持度阈值范围为1%～3.5%，实验执行时间比较结果见图4.mushroom包含8 124个事务，119个事务项，平均事务长度23，实验选择支持度阈值范围为5%～30%，实验执行时间比较结果见图5.Accidents包含340 184条记录、572个事务项，平均事务长度为45，实验选择支持度阈值范围为40%～90%，实验执

图4 T10I4D100K数据集执行情况

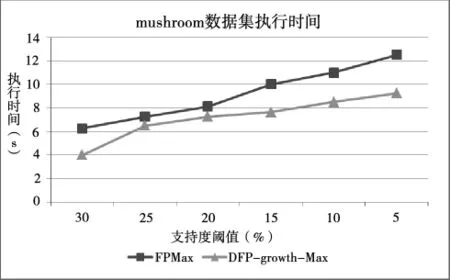
图5 mushroom数据集执行情况

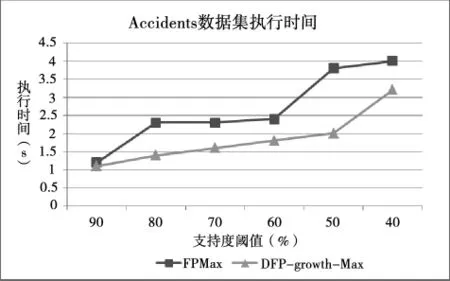
图6 Accidents数据集执行情况

实验结果表明，与FPMax算法相比，DFP-growth-Max算法在稀疏数据集和稠密数据集上都有较好的运行效率，DFP-tree建树方法具有更快的建树效率，利用DFP-数组可以快速地挖掘最大频繁模，DFP-growth-Max算法是基于DFP-tree建树方法和DFP-数组技术的，因此具有较快的挖掘效率.