基于矩阵相乘的Apriori改进算法
2018-10-23邹书蓉
王 蒙 方 睿 邹书蓉
(成都信息工程大学计算机学院 成都 610225)
1 引言
最经典的Apriori算法广泛用于商业、教育、卫生等领域,于 1994 年被 Rakesh Agrawal等提出[1],2007年Apriori算法被列为数据挖掘十大算法之一[2],最近几十年里,大量学者为了改进Apriori算法产生大量的候选集频繁和反复地扫描数据库的问题提出了很多卓有成效的方法。徐章艳等[3]提出了Apriori算法的三种优化方法,对连接程序中的候选集进行优化剪枝,删除在扫描数据库时不必要比较的事务等做了改进。但是每次还要反复回扫数据库。一些国内外学者用把存储为布尔矩阵,通过项集向量“与”的操作来代替扫描数据库,通过对矩阵的操作实现对候选集的剪枝大大提高了算法效率[4~6]。文献[7~9]中通过一次性扫描数据库得到的Tid表(项、事务、支持度),这个表格维护在内存中,通过直接操作此表,这样就不用反复扫描数据,在用频繁项集连接生成候选项集时,直接把项的事务向量求交集。但是没有在算法运行中删除一些不必比较的事务,有大量的候选集生成频繁集时非常耗时。
Apriori算法就是通过反复多次扫描事务数据库来计算候选集的支持度,这样得到频繁项集后产生关联规则。但是随着大量学者的深入研究,Apriori也存在缺点,对于超长长度的候选集集合,每计算一个项集的支持度都要扫描数据库,频繁的扫描使I/O不堪重负。基于以上可见都是在针对Apriori的常见缺点进行改进。本文不仅针对Apri⁃ori算法常见缺点进行改进还对事务集进行精简删除和连接步剪枝步过程优化。
2 Apriori算法基本性质和改进算法的定义
2.1 Apriori算法基本性质
针对以上的Apriori算法缺点,下面给出Apriori算法的性质并加以证明。
性质1[10]:对于频繁项集的任何非空子项集都是频繁项集。
推论1[10]:根据性质1,它的逆否命题也是成立的,如果一个非空项集不是频繁的,那么它的超集也不是频繁的,它的超集不作为候选项集。
性质 2[11]:设 Lk为频繁 k-项项集集合,其中 I1∈Lk,I1的前k-1项与I2的前k-1相同,若I1的第k项与I2的第k项组成的项集是频繁2-项集,则I1与I2连接成的候选(k+1)-项集的所有非空子集都是频繁项集,否则根据推论2得知此候选(k+1)-项集不可能为频繁项集。
证明:候选(k+1)-项集的子集有三类:I1的子集、I2的子集、I1的第k项与I2的第k项组成的项集的子集,因为I1与I2为频繁项集,又因I1的第k项与I2的第k项组成的项集是频繁2-项集,根据性质1得知候选(k+1)-项集的非空子集都是频繁项集。
性质3:若事务集T中含有可连接的频繁k-项集的数量小于等于1,则T不可能包含频繁(k+1)-项集。
证明:反证法,假设T具有频繁(k+1)-项集,则按照两个频繁k-项集的连接成频繁(k+1)-项集的方式,T中至少有两个可连接的频繁k-项集。与题设矛盾,故原命题成立。
性质4:在一个频繁项集集合中,若其中的某个项集不能与其相邻的频繁项集连接,则此项集一定不能与此集合中所有的频繁项集连接。
证明:反证法,假设此项集I能与不相邻的项集I'相连接,则I的前k-1项与I'的前k-1相同,又因项集都是按照字典顺序排列,所以从I到I'的所有项集的前k-1项相同,也就是说从I到I'的所有项集都可以连接,又因I'与I不相邻,所以I也能与相邻的项集连接这与题设矛盾,故原命题成立。
2.2 改进算法的定义
为了更好地说明改进的算法,给出改进算法的相关定义。
定义1:相邻频繁项集,k=1时频繁1-项集都是相邻的;k≥2时,设Lk为频繁k-项项集集合,p为Lk内的项集个数,其中 Ii-1∈Lk、Ii∈ Lk、Ii+1∈ Lk,1<i<k时,若 Ii与 Ii-1或者 Ii与 Ii+1的前 k-1 相同,则判定 Ii为相邻频繁项集;i=1时,若I1与I2前k-1相同,则I1为相邻频繁项集;i=k时,若Ik与Ik-1前k-1相同,则Ik为相邻频繁项集。
定义2:相邻频繁项集事务矩阵SN,候选项集事务矩阵SC,候选项集矩阵H,设l为事物的个数,m为相邻频繁k-项集的个数,n为候选(k+1)-项集的个数,设{T1,T2,…,Tl}为数据库事务集集合T,其中k≥1。
SN为一个l×m矩阵,设{I1,I2,…,Im}为相邻频繁k-项集集合Nk,若事务Ti中包含项集Ii则snij=1反之snij=0,其中(i≤l,j≤m)。定义数组X存储SN的各行之和也就是统计各事务所包含项集的个数,根据性质3,找到X中小于2的元素所对应的事务,删除该事务所对应的SN矩阵的行,得到的矩阵为SN'。
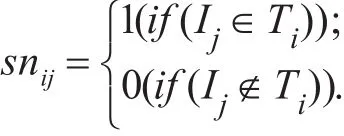
H为一个m×n矩阵,设{I'1I'1,…,I'n}为候选(k+1)-项集集合 Ck+1,若候选集 I'j包含 Ii,则 hij=0.5,反之hij=0,其中Ii∈Nk,(i≤m,j≤n)。
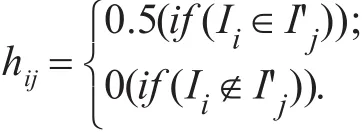
SC为一个l×n矩阵,若事务Tu中包含项集I'v则scuv=1,反之scuv=0,其中(u≤l,v≤n),Tu∈T,I'v∈Ck+1,本文定义:

即

3 改进的Apriori算法
本文对Apriori算法进行这三个方面的改进,反复扫描数据库;把不必要的事务集加入下次数据库扫描;连接步剪枝步比较过程复杂。
改进方法,只扫描一次数据库,存储为布尔矩阵[12],利用频繁k-项集的事务矩阵与候选(k+1)-项集矩阵相乘得到候选(k+1)-项集事务矩阵,从而求出频繁(k+1)-项集;根据性质3删除不必要的事务;在判断连接过程中删除不相邻频繁项仅使用可以相连接的频繁项进行连接并优化连接过程。根据性质2对剪枝步进行优化。其中本文所有事务或项集中的项都按字典顺序排列。
3.1 算法思想
通过扫描一次事务数据库产生候选项集事务矩阵SC,计算支持度得到频繁项集L,只扫描一次数据库即可,减少I/O时间。对SC进行压缩精简,得到SN与相邻频繁项集集合Nk,对SN删除不必要的事务,减少参加下次运算的事务数量,得到SN',然后通过相邻频繁项集连接剪枝生成H,减少连接比较次数进一步优化算法,分别删除SN'与H不能组成候选项集的相邻频繁项集对应的列与行。矩阵相乘运算SN'*H=SC再次得到下一个候选项集事务矩阵SC,多次重复SN'*H=SC直到Nk为空时结束。
3.1.1 连接步的优化
相邻频繁项集集合Nk,频繁项集集合Lk,改进算法使用Nk来进行连接,由性质4可知,使用Nk或Lk连接得到的候选项集一致,这样就避免和非相邻项集进行多次比较,加快了连接速度。改进算法对连接过程也进行了优化,设I,I'∈Nk,若I与I'不能连接,显然I不能与I'之后的所有项集连接,这样就不用比较I'之后的项集,加快了连接速度,从而提高了算法效率。
3.1.2 生成频繁项集
候选项集事务矩阵SC,最小支持度min_sup,定义支持度数组W存储SC各列之和。
生成频繁1-项集,扫描数据库生成布尔矩阵,也就是候选1-项集事务矩阵SC,候选1-项集集合C1,通过步骤通过W对支持度小于min_sup的SC的列进行删除和对应C1的项集进行删除得到频繁1-项集L1,由定义1知N1=L1。
k≥1时,生成频繁(k+1)-项集,1)对相邻频繁k-项集集合Nk进行连接步后得到候选(k+1)-项集集合Ck。2)由性质2可对Ck+1进行剪枝,同时生成候选项集矩阵H。3)分别删除SN'与H不能组成候选项集的相邻频繁项集对应的列与行。然后SN'*H=SC此时得到的是候选(k+1)-项集事务矩阵SC。4)通过W对支持度小于min_sup的SC的列进行删除和对应Ck+1的项集进行删除得到频繁(k+1)-项集Lk+1。5)由定义1得到Nk+1,对SC矩阵删除非相邻的频繁项集的列得到SN,SN删除不必要的事务后得到 SN'。循环执行1)~5)直到Nk为空,结束。
3.2 改进算法伪代码描述
输入:事务数据库D,最小支持度min_sup。
输出:频繁k-项集Lk,和Lk所包含项集的个数LCountk。
Begin
扫描数据库D,生成布尔矩阵。生成频繁1-项集。
打印输出 LCount1,L1;
While Nk非空
For r=1 to m(m为Nk中项集的个数)
For i=r to m-1
If(Nk{r}与Nk+1{i+1}满足连接条件)
Then NEW=Nk{r}Nk+1{i+1}连接的结果;
If(根据性质2,NEW的子集是频繁项集)
Then将NEW写入Ck+1;
将Nk与Ck+1映射值存入生成的矩阵H;
Else Break;EndIf
Else Break;EndIf EndFor EndFor
分别删除SN'与H不能组成候选项集的相邻
频繁项集对应的列与行。
SN'*H=SC;
Lk+1=Ck+1{W≥min_sup};
打印输出 LCountk+1,Lk+1;
删除SC中W<min_sup所对应的列;
k=k+1;
For(s=1 to n)(n为Lk+1中的项集个数)
If(Lk+1{s}是相邻的频繁项集)
Then把Lk+1{s}写入Nk+1中;
生成非相邻频繁项集的索引数组Del;
EndIf EndFor
SN←删除SC中的Del对应的列;
SN'←删除SN中数组X≤1所对应的行;
EndWhile End
4 算法实例和实验对比
4.1 算法实例分析
通过实例来说明改进算法思想的运行流程,表1为数据库的事务列表。

表1 数据库事务列表[10]
设min_sup=2,改进的算法运行过程如下。其中会给出关键矩阵内容。
扫描数据库D,得到布尔矩阵SC,C1={I1,I2,I3,I4,I5},支持度数组W ≥ min_sup则频繁1-项集集合L1={I1,I2,I3,I4,I5},由定义1知SN=SC,N1=L1,X≥2由定义2中的SN生成SN'的过程得知SN=SN'。

第1次循环,N1不为空,对N1连接步得到C2={{I1,I2},{I1,I3},{I1,I4},{I1,I5},{I2,I3},{I2,I4},{I2,I5},{I3,I4},{I3,I5},{I4,I5}},根据定义2中的H矩阵定义,组成H矩阵,其中例如12代表{I1,I2}。然后SN'*H=SC,此时的SC是候选2-项集矩阵。

依据W ≥ min_sup从C2可得L2={{I1,I2},{I1,I3},{I1,I5},{I2,I3},{I2,I4},{I2,I5}},同时对W<min_sup所对应SC的列进行删除,然后通过定义1删除L2非相邻频繁项集得到N2={{I1,I2},{I1,I3},{I1,I5},{I2,I3},{I2,I4},{I2,I5}},同时把SC 非相邻的项集的列删除得到SN,根据性质3,数组 X≤1所对应的SN的行删除得到SN'。

第2次循环,N2不为空,对N2进行连接得到C3={{I1,I2,I3},{I1,I2,I5},{I1,I3,I5},{I2,I3,I4},{I2,I3,I5},{I2,I3,I5}}。根据性质2剪枝后的C3={{I1,I2,I3},{I1,I2,I5}}同时生成H,分别删除SN'与H不能组成候选项集的相邻频繁项集集合{{I2,I3},{I2,I4},{I2,I5}}对应的列与行。然后SN'*H=SC,其中123表示{I1;I2;I3}。

此时的SC是候选3-项集矩阵,依据W≥min_sup从C3可得 L3={{I1,I2,I3},{I1,I2,I5}},然后得到N3={I1,I2,I3},{I1,I2,I5}},同时把SC非相邻的项集的列删除得到SN,根据性质3,数组X≤1所对应的SN的行删除得到SN'。

第3次循环,N3不为空,对N3进行连接得到C3={{I1,I2,I3,I5}}。根据性质2剪枝后的C3=空,N4也为空。
第4次循环,N4为空,算法结束。
4.2 实验对比分析
4.2.1 实验环境和数据集
将Apriori算法和本文的改进的算法在MAT⁃LAB R2015b中实现,计算机实验环境为Win7x64操作系统,8GRAM,1T硬盘,Intel Core-i5处理器,数据集采用经典的MushRoom数据集,下载网址:http://fimi.ua.ac.be/data/,该数据集有8124个事务,119个项。
4.2.2 实验结果
表 2中 1(0.3)表 示 的 是 Apriori算 法 在min_sup=0.3的情况下,2(0.3)表示的是改进后算法在min_sup=0.3的情况下。k的值就是频繁k-项集。

表2 两种算法所得到的频繁项集个数对比
两种算法在119个项,8124个事务的mushroom数据集,最小支持在0.3~0.9之间,同种环境下运行得到频繁集结果一致。改进算法的准确性得到验证。

图1 不同支持度下两种算法的运行时间对比

图2 不同项的两种算法运行时间对比
实验一在mushroom数据集下,min_sup在0.3~0.9之间变化,比较两种算法的运行时间,从图1中可以看出在支持度逐渐增大过程中两种算法的运行时间都存在着下降最后趋近于0,但是Apriori算法的时间在支持度小的时候运行时间明显大于改进的算法,改进的算法的在不同的min_sup情况下运行时间没有很大的波动。
实验二在不同mushroom数据集的项的个数,在min_sup=0.3得情况下两种算法运行的时间比较,从图2可以看出随着项的个数增长两种算法运行时间都有所增长,开始两种算法的时间相差不是太大,后面的时候Apriori算法的时间远远大于改进的算法,说明原算法面对项数多的数据集的情况下严重影响运行时间,改进算法时间增长平缓。
综上,改进算法在不同支持度下和不同项的情况下表现出更好的性能。
5 结语
本文提出基于矩阵改进的Apriori算法,通过矩阵相乘改进了Apriori算法反复多次扫描数据库巨大的I/O负载的问题[13],改进了连接剪枝候选集的方式避免产生巨量的候选集大大提高了算法效率,删除不必要的事务集减少了不必要的比较,通过实验可以看出改进算法大大的降低了运行时间,改进算法的效果明显。未来的工作是让算法在大数据集的情况中表现很高的性能,通过优化矩阵存储方式减少内存负载[14],通过并行方法[15~16]优化矩阵相乘等方式让算法具有更好的效率。
