基于PSO-GA混合算法的移动采集节点路径优化研究

徐丽萍

（安徽三联学院 电子电气工程学院，安徽 合肥230009）

在无线传感网中，传统的数据采集策略是采用多级跳的方式，但这种方式并不完美.一是多级跳的方式让靠近固定sink节点的静态传感器承担了较大的通信负载，容易形成能量空洞；二是在大规模随机部署的无线传感网中，因地理环境等因素的影响，较难实现自组织成为全联通网络，传统的多级跳的方式无法解决这种稀疏的非连通无线网中的数据采集问题.随着机器人技术的发展，在无线传感网中使用具有移动能力的节点采集数据成为了可能.在无线传感网中引入移动节点不但可减小静态传感器节点的通信负载，延长无线传感网的生存时间，还可解决稀疏的非连通网络数据采集问题.

近年来，学者们对具有移动节点的无线传感网中的路径规划问题做了很多研究.2012年任条娟等人利用节点的度值构建了sink节点移动路径［1］.陈友荣等人考虑多个斯诺克节点的移动，根据网格潜能值确定sink节点的锚点，获得sink节点的最短移动路径［2］.俸皓等人为通信范围建模为圆形区域的无线传感网提出了一种基于萤火虫算法的移动sink节点路径规划方法［3］.朱正伟等人将移动sink节点的路径规划问题看成是一个带邻域的旅行商问题，提出了混合免疫粒子群算法来求解该问题［4］.Ma M等人引入移动采集节点，移动采集节点从静态sink节点出发，遍历每个传感器节点，收集传感器采集到的数据并带回sink节点，建立了基于最短路径的移动采集节点路径优化模型［5］.俸皓等人利用多移动采集节点进行数据采集的方式，提出了一种基于多移动节点的多目标数据采集策略，设计了混合遗传算法来求解多个移动节点的规划路径［6］.针对具有单移动采集节点的无线传感网络的数据采集问题，笔者以最大化移动采集节点的数据采集效率为目标，基于PSO-GA混合算法对移动采集节点的数据采集路径进行优化，并通过实验仿真证明了数据采集策略的有效性.

1 问题描述

假定二维平面部署了n个静态传感器节点（位置固定）用于感知周围数据，一个位置固定的sink节点，每个静态传感器节点采集到的数据都会被暂存到节点的缓存区内，若在移动采集节点到达之前，缓存区的数据量已经达到存储上限，则通过多级跳的方式传回sink节点.移动采集节点从sink节点出发，依次访问各个静态传感器节点，接收静态传感器缓存中的数据，再回到sink节点，形成一条回路.

假设：静态传感器节点向移动采集节点传送数据的速率均为r，缓存区存储采集数据量的上限为C.移动采集节点的移动速率为v，数组s表示路径，s（k）表示第k个访问的节点，移动采集节点到达第k个节点的时间表示为ts(k)，移动采集节点从sink节点出发时路径上第k个静态传感器节点缓存区中的数据量表示为Gs(k)，路径上第k个静态传感器节点采集数据的速率表示为Rs(k)，路径上第k个静态传感器节点缓存中的数据量表示为：

其中：

即从sink节点出发到到达第k个静态传感器节点路径上需要的时间与跟前k-1个静态传感器进行数据传送所需的时间之和.

移动采集节点的采集效率可以表示为数据采集量与数据采集路径总长度的比值.故目标函数可以表示为：

2 基于PSO-GA混合算法的求解方法

2.1 算法构造

GA算法和PSO算法都是经典的智能优化算法，PSO-GA混合算法克服了单一PSO算法易陷入局部最优点的缺点，改善了单一GA算法收敛精度低的问题，相比单一算法而言具有更好的全局稳定寻优的能力，提高了算法的性能［7］，在求解NP-hard问题中得到了广泛地应用［8-10］.无线传感网中的移动采集节点路径规划问题可以看成是时变的旅行商问题，属于NP-hard问题.针对单移动采集节点的路径规划问题，文中基于PSO-GA混合算法进行求解.GA算法和PSO算法混合方式有多种，笔者采用的是将GA算法中的交叉操作和变异操作嵌入到PSO算法中，粒子同个体极值及群体极值进行交叉操作产生新粒子，使个体（群体）极值的优良基因可被很好的继承，而变异操作可以使粒子个体通过微调得到新个体，保证了群体的多样性.

2.1.1 个体编码

粒子个体编码采用整数编码的方式，每个粒子代表一条路径，若有n个静态传感器，则静态传感器节点编号从1开始到n，sink节点编号为0.如果需要遍历的静态传感器节点数为10，则个体编码为{0，2，5，7，8，9，10，1，4，3，6}，表示从 sink 节点 0 出发，遍历所有静态传感器节点，回到 sink 节点 0，其中个体编码长度为n+1.

2.1.2 适应度值

粒子适应度值表示为采集的数据总量与遍历路径长度之间的比值，计算公式为：

其中，每个静态传感器节点缓存中的数据量ds(k)是随着时间不断变化的，移动采集节点访问静态传感器节点的顺序不同，到达静态传感器节点的时刻不同，需要传送的数据量ds(k)大小也不同.故每个静态传感器节点缓存中的数据量由公式（1）和公式（2）递归计算得出.

2.1.3 交叉操作

粒子个体通过与粒子个体极值以及粒子群体极值交叉来更新.具体操作如下：随机产生两个位置a1、a2，取个体（或者群体）极值pg的基因片段cross={pga1….pga2}.依次找出粒子中跟基因片段cross重复的节点编号并删除.将基因片段cross复制到粒子中的后a2-a1+1位中.

例如：原粒子（0，2，5，7，8，9，10，1，4，3，6），个体极值（0，3，4，6，2，5，9，10，1，8，7）.

随机生成的位置为a1=3，a2=5，则基因片段cross={4，6，2}.依次删除粒子中跟基因片段相同的节点编号， 则粒子变为 （0，5，7，8，9，10，1，3）.将基因片段 cross复制到粒子的后 3位中， 则生成的新粒子为（0，5，7，8，9，10，1，3，4，6，2）.

由于移动采集节点是从sink节点出发的，所以可行解的第一个元素的值一定是sink节点编号0，所以ai的取值范围应为1＜ai≤n+1.

2.1.4 变异操作

随机产生两个位置号a1、a2，1＜ai≤n+1，将粒子中a1、a2，两个位置上的静态传感器节点编号进行交换，产生新粒子个体.

2.1.5 粒子更新规则

若新的粒子优于旧粒子，则更新粒子，否则保持原来的粒子不变.

2.2 算法步骤

Step 1：控制参数的设置：设置粒子群的规模Nmax及迭代次数N.

Step 2：按2.1.2的方法构造初始解.

Step 3：按2.1.3的方法，个体与个体极值交叉产生新个体，计算个体的适应度值并按粒子更新规则更新粒子.

Step 4：按2.1.3的方法，个体与群体极值交叉产生新个体，计算个体的适应度值并按粒子更新规则更新粒子.

Step 5：按2.1.4的方法对个体进行变异操作产生新的个体，计算个体的适应度值并按粒子更新规则更新粒子.

Step 6：更新当前个体最优值及群体最优值.

Step 7：如果当前迭代次数 n＜N，转 Step 3，否则，退出.

3 实验仿真

为方便验证可靠性，在文献6提供的公开数据集作为算法的测试用例，取sink节点坐标值为（500，500），取20个静态节点，坐标值及其初始数据量见表1，静态传感器节点向移动采集节点发送数据的速率r取20 kb/s.

表1 静态节点坐标

设置迭代次数N为133，及粒子群的规模Nmax为1 000.静态传感器节点的缓存存储数据上限C取2 Mb，移动采集节点移动速度v取3 m/s.连续运行10次得到的数据见表2.

表2 运行结果

连续运行10次中优化结果最好的一次，寻得近似最优路径见图1，路径为：1→3→7→16→19→4→13→2→17→8→5→20→11→18→15→12→21→10→14→6→9.其采集数据量与路径长度的比值为 6.79，算法优化过程见图2，程序运行时间为10.487 s.

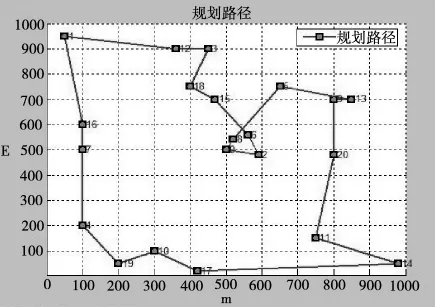
图1 PSO-GA混合算法规划的路径

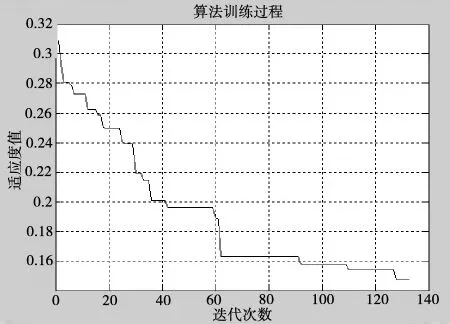
图2 PSO-GA混合算法优化过程

模拟退火算法（SA）是一种随机搜索方法，已被理论和实际应用验证是一种全局最优算法，适合求解大规模组合优化问题，在旅行商问题的求解中得到的广泛使用［11-12］.为方便与模拟退火算法进行比较，同一个测试用例也使用模拟退火算法进行求解.初始温度取1 000，终止温度取0.001，降温速率取0.95，运行10次，求得数据见表2，其中优化结果最好的一次，寻得近似最优路径见图3，路径为：1→2→13→4→16→19→6→10→14→9→3→21→15→12→18→11→5→20→8→17→7，求得采集数据量与路径长度的比值为5.75，算法优化过程见图4，程序运行时间为10.822 s.

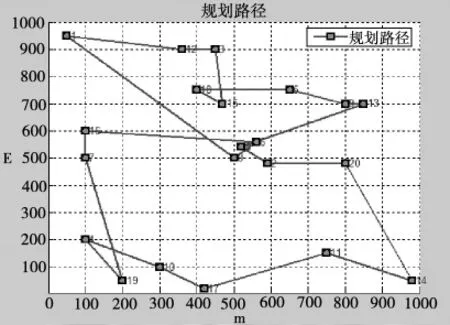
图3 模拟退火算法规划的路径

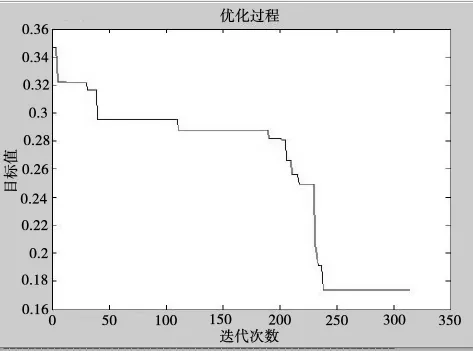
图4 模拟退火算法优化过程

通过表2可以看出，PSO-GA混合算法寻得的近似最优路径的目标值（采集数据量与路径长度的比值）最低为5.21 kb/s，最高为6.79 kb/s，平均值为5.77 kb/s.模拟退火算法寻得的近似最优路径的目标值最低为3.67 kb/s，最高为5.76 kb/s，平均值为4.84 kb/s.可见文中基于PSO-GA混合算法设计的移动采集节点的路径规划方法寻优比较稳定，寻得的近似最优解更接近最优解.通过图2和图4对比，可以看出PSO-GA混合算法比模拟退火算法收敛速度快.

4 结语

针对具有单移动采集节点的无线传感网中的数据采集路径规划问题，笔者利用PSO-GA混合算法进行了求解，实验仿真证明PSO-GA混合算法全局寻优能力稳定，寻得的近似最优路径可以有效地提高移动采集节点的数据采集效率.且与模拟退火算法相比，收敛速度快，寻得的近似最优解更佳.针对具有单移动采集节点无线传感网设计数据采集策略的方法，对具有多个移动采集节点的无线传感网也有借鉴意义，下一步可尝试将该算法应用于求解具有多移动采集节点的无线传感网中的数据采集路径规划问题.