自适应严格收敛非奇异终端滑模制导律
2019-05-25李晓宝赵国荣张友安郭志强
李晓宝,赵国荣,张友安,郭志强
1. 海军航空大学 岸防兵学院,烟台 264001 2. 海军航空大学 大学参谋部,烟台 264001 3. 烟台南山学院 电气与电子工程系,烟台 265713
为了使作战毁伤效果最大化,导弹以较小的脱靶量拦截目标的同时还要求具有特定的终端攻击角度。对于静止或者机动能力较弱的目标,比例导引律因其制导效果好,便于实现的优点而被广泛的应用[1-2],但对高机动目标的制导效果却并不理想[3]。针对机动目标的拦截问题,应用现代控制理论进行导弹末制导律的设计近些年开始成为研究的热点,如最优控制制导律[4-5]、H∞控制制导律[6]、微分对策制导律[7]。
对于系统不确定性和外界的扰动,滑模控制具有较强的鲁棒性,并且相比于最优控制制导律,不需要对剩余时间进行估计,因此在制导律设计中得到了深入研究[8]。传统滑模制导律其弹目视线(Line of Sight, LOS)角在制导过程中收敛时间是趋于无穷的,而终端滑模控制(Terminal Sliding Mode Control, TSMC)通过引入非线性滑模面确保了系统状态能够在有限时间内收敛[9]。针对导弹在拦截高机动目标时末制导时间通常较短的特点,有限时间收敛控制能够加快制导系统收敛速率,缩短制导时间。应用TSMC方法设计拦截机动目标的末制导律近些年得到了广泛的研究[10-16]。但是传统的TSMC方法会出现奇异现象[17],现有的终端滑模制导律在解决滑模面奇异性问题时通常采取两种办法:一是采取滑模面转换的形式避免奇异性问题,例如文献[10]在滑模面进入奇异区域时将其转换为普通的二次函数形式的滑模面,但是因为转换滑模面的存在,制导系统状态变量最终不能在有限时间收敛到零;二是设计新型的非奇异终端滑模面,例如文献[11-12] 构造了一种非奇异终端滑模面,在此基础上设计了一种非奇异终端滑模制导律,文献[13-15] 进一步给出了快速非奇异终端滑模制导律的设计方法,提高了制导系统的收敛速率。但是,文献[11-15]在制导过程中存在着非严格有限时间收敛的问题,即制导系统在滑模面到达过程中不是严格有限时间收敛的,存在着非收敛因子,需要单独分析非收敛因子是否为滑模到达阶段的吸引子,而且非收敛因子的存在减缓了滑模面的收敛速率。文献[16]特别指出了这个问题并为此设计了一种新型的严格收敛非奇异终端滑模制导律,然而其设计的滑模面并不是光滑的,而且制导系统状态变量最终并不能收敛到零,只能收敛到一个未知的有界区域内。
此外,在研究拦截机动目标的末制导问题时,采用终端滑模设计制导律需要预先知道目标的机动,然而实际情况中目标的机动大多数是未知的,文献[14,18]在设计制导律过程中假设目标机动存在一个已知的上界,但是通常目标机动的上界也难以测量。自适应控制由于其在控制过程中具有不需要知道外部扰动任何信息的优点,应用到制导律设计中可以有效地解决目标机动未知的问题[19-20]。
针对机动目标的终端角度约束末制导拦截问题,考虑到上述文献研究的不足,本文设计了一种新型的严格收敛非奇异终端滑模面,该滑模面不仅连续光滑并且有效避免了奇异性问题;然后,通过Lyapunov稳定性理论证明了基于此滑模面设计的制导律不仅能够使得制导系统在滑模面到达阶段是严格有限时间收敛的,具有更快的收敛速率,而且确保了终端角度误差和LOS角速率最终是有限时间内收敛到零的,提高了终端角度约束的精度。此外,设计了一种针对目标机动上界的自适应律使得制导律设计过程中不需要预先知道目标的机动信息,增强了制导系统对外部干扰的鲁棒性。最后,通过仿真对该制导律的性能进行了分析。
1 问题描述和相关引理
1.1 问题描述

图1 导弹目标运动关系Fig.1 Missile target engagement geometry
导弹末制导拦截过程可以简化为在二维平面内进行,如图1所示r和q分别代表导弹M和目标T之间距离和弹目LOS角,γM和γT分别代表M和T的航迹角,假定M和T速度恒定分别记为VM和VT,aM和aT分别代表M和T的法向加速度。那么制导系统的运动学方程可表示为
(1)
(2)
导弹末制导终端攻击角度θimp为终端拦截时导弹和目标速度之间的夹角,若γTf和γMf分别为导弹和目标的终端航迹角,可知
θimp=γTf-γMf
(3)
VMsin(γMf-qd)=VTsin(γTf-qd)
(4)

(5)
对于某一具体的拦截过程,ν是固定的,若目标是静止的,则γTf=0;当目标作非机动运动,则γTf是可测的;若目标是机动的,则γTf可以通过弹上的跟踪滤波器得到。若γTf已知,对于某一期望的θimp,则由式(5)可知存在唯一的qd与之对应;对于某一期望的qd,由式(3)和式(4)可知存在唯一的γMf和θimp与之对应。因此,导弹终端攻击角度θimp与终端LOS角qd存在着一一对应关系[21]。因此,导弹末制导终端攻击角度θimp约束可以转化为期望的终端LOS角qd约束的问题。
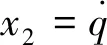
(6)
式中:d=cos(γT-q)aT为由目标机动产生的制导系统外部扰动
假设1假设Δ为一正常数,代表目标机动aT最大值,那么可知|d|≤Δ。
通过设计导弹法向加速度aM使LOS角跟踪误差x1以及LOS角速率x2在有限时间内收敛到原点,导弹便能够确保以期望的终端LOS角qd精确命中目标。
1.2 基本引理
引理1[17]假设存在原点邻域U∈Rn上的C1光滑正定函数V(t),且V(t)满足:
(7)
式中:a,b>0, 0<γ<1,t>t0,t0为系统初始时间。那么,该函数将在有限时间收敛到零,且相应的收敛时间tf满足:
(8)
引理2[22]假设存在原点邻域U∈Rn上的C1光滑正定函数V(t),且V(t)满足:
(9)
式中:λ>0, 0<γ<1,t>t0。那么,该函数将在有限时间收敛到零,且相应的收敛时间tf满足:
(10)
2 制导律设计
2.1 严格收敛非奇异终端滑模面构造
针对终端滑模控制存在奇异性问题,文献[12] 设计了一种非奇异终端滑模面
s=x1+αsigq(x2)
(11)
式中:α>0, 1 (12) 制导系统在滑模面到达阶段由Lyapunov稳定性理论得到 (13) 图2 制导系统变量的收敛过程Fig.2 Convergence process of guidance system 文献[16]针对此问题设计了一个严格收敛非奇异终端滑模面: (14) 式中:α,β>0,a>0,γ>1。对滑模面(14)求导可得 (15) 文献[10]针对滑模面奇异性问题,提出了一种转换滑模面的方法: s=x2+l1x1+l2g(x1) (16) 式中:l1>0,l2>0,g(x1)∈R定义为 (17) 式中:0<γ<1,α1=(2-m2)εγ-1,α2=(m2-1)εγ-2,ε为一个小的正常数。 虽然基于滑模面(16)设计的制导律[10]虽然不存在上述非严格有限时间收敛的问题,但是因为转换滑模面的存在,系统状态变量x1,x2在滑动阶段最终只能有限时间收敛于{(x1,x2)|x1≤ε,x2≤α1ε+α2εγ},而并不能严格的有限时间收敛到零。 为了解决上述非奇异终端滑模制导律设计中存在的问题,本文设计了一种严格收敛非奇异终端滑模面 s=x1+α(p|x1|+e-p|x1|-1)· (1-e-q|x2|)sign(x2)+βsigγx2 (18) 式中:α,β>0, 0<αp<1,q>0, 1<γ<2。对滑模面s求导可得 sign(x1x2)+[αq(p|x1|+e-p|x1|-1)· (19) 定理1对于制导系统(6),若采用本文构造的滑模面(18),如果制导指令aM设计为 (20) (21) 则有如下结论成立: 2) 滑模变量s严格有限时间内收敛于零。 3) 制导系统(6)的状态变量x1、x2有限时间内收敛于零。 证明:该定理证明过程分为如下3步。 1)考虑如下Lyapunov函数 (22) 根据式(19)~式(21),那么Lyapunov函数V的导数可以写为 αpx2(1-e-p|x1|)(1-e-q|x2|)sign(x1x2)+ (23) 2)考虑如下Lyapunov函数 (24) 对Lyapunov函数V1求导,代入式(19)和式(20) 可得 (1-e-p|x1|)(1-e-q|x2|)sign(x1x2)+ (25) (26) 式中:η为个任意小的正常数。那么 (27) 因此,可以得到 (28) 因为φ(x1,x2)≥0,当且仅当x1=x2=0时等号才成立,所以由式(28)以及引理1可知,制导系统(6)在滑模面到达过程中严格有限时间收敛到s=0。 3)考虑如下Lyapunov函数 (29) 因为0≤1-e-q|x2|≤1, 0≤p|x1|+e-p|x1|-1≤p|x1|,当制导系统(6)状态量x1、x2到达滑模面(18)时,由s=0可知x1x2≤0,且此时 (30) 对Lyapunov函数V2求导,代入式(30)可得 (31) 注4由于符号函数sign(s)的存在,制导律(19)是非连续的,可能会引发颤振现象。为了减少震颤,符号函数sign(s)可采用双曲正切函数tanh(s/ξ)近似代替,ξ是一个小的正常数。因此,制导律(20)就可以修改成如下形式 k1s+k2sigγ1s] (32) 式(32)即本文最终设计的考虑终端角度约束的自适应严格收敛非奇异终端滑模制导律(Adaptive Strictly Convergent Nonsingular Terminal Sliding Mode Guidance,ASCNTSMG)。 为了更全面地分析ASCNTSMG的制导效果,在仿真中引入了与其他现有制导律的对比。 文献[12]设计一种自适应非奇异终端滑模制导律(Adaptive Nonsingular Terminal Sliding Mode Guidance, ANTSMG) (33) 文献[10]设计一种自适应非奇异快速终端滑模制导律(Adaptive Nonsingular Fast Terminal Sliding Mode Guidance, ANFTSMG)。 (34) 同时为了更好地分析ASCNTSMG的制导性能,考虑如下3种不同的目标机动情况: 1)aM=7gcos(πt/4)。 2)aM=7g。 3) 当t≤5 s时,aM=7g;当t>5 s时,aM=-7g。 此外,文献[15]提出了平均拦截加速度aME的概念来评估制导指令的大小,其定义为 (35) 式中:N为总的仿真步数;aM(k)为第k步的制导指令仿真值。 假设导弹拦截目标时期望的终端LOS角qd为20°,在3种不同的目标机动情况下对制导律ASCNTSMG、 ANTSMG和ANFTSMG的制导性能进行对比,仿真结果如图3~图5以及表1~表3所示。 对于拦截高机动目标,导弹末制导时间通常较短。然而为了满足LOS角和LOS角速率有限 图3 第1种目标机动下导弹拦截Fig.3 Intercepting target in Case 1 时间收敛的要求,导弹在末制导前期通常需要进行较大的机动使得导弹尽快的对准目标,但是导弹的机动能力有限,因此制导指令在末制导初始阶段会出现饱和现象,ANTSMG和ANFTSMG在相同的仿真场景下也出现了饱和现象。饱和现象的出现并不会影响制导系统的稳定性,但会导致滑模面和系统变量收敛时间的增加。如图6所示,在第3种目标机动下,相比于不考虑制导指令饱和的情况,ASCNTSMG依旧能够使得滑模面s 图4 第2种目标机动下导弹拦截Fig.4 Intercepting target in Case 2 图5 第3种目标机动下导弹拦截Fig.5 Intercepting target in Case 3 表1 第1种目标机动下仿真结果Table 1 Simulation results in Case 1 制导律拦截时间/s脱靶量/mLOS角误差/(°)aME/(m·s-2)ASCNTSMG17.22810.02150.0279102.4745ANTSMG19.61580.03050.0180173.7820ANFTSMG17.73340.02570.0443123.7496 表2 第2种目标机动下仿真结果Table 2 Simulation results in Case 2 表3 第3种目标机动下仿真结果Table 3 Simulation results in Case 3 图6 不考虑制导指令饱和的仿真对比Fig.6 Simulation comparison without saturation 和LOS视线角q在有限时间内收敛,但是收敛时间分别增加了2 s和1 s左右。 假设导弹拦截目标时期望的终端LOS角qd=20°,目标采取aM=7gcos(πt/4)进行机动,导弹的初始航迹角γM0分别为30°,60°和90°。针对ASCNTSMG进行仿真分析,结果如图7以及表4所示。 图7 以不同的初始航迹角拦截目标Fig.7 Intercepting target with different initial flight path angles 表4 以不同的初始航迹角拦截目标时仿真结果 Table 4 Simulation results of intercepting target with different initial flight path angles 初始航迹角(°)拦截时间/s脱靶量/mLOS角误差/(°)aME/(m·s-2)3016.61180.02260.037897.47076017.22810.02150.0279102.47459019.39240.0163-0.0323134.1757 假设导弹拦截目标时初始航迹角γM0=60°,目标采取aM=7gcos(πt/4)进行机动,期望的终端LOS角qd分别为20°,30°,40°。针对ASCNTSMG进行仿真分析,结果如图8以及表5所示。 图8 以不同的期望终端LOS角拦截目标Fig.8 Intercepting target with different desired LOS angles 表5 以不同的期望终端LOS角拦截目标时仿真结果 Table 5 Simulation results of intercepting target with different desired LOS angles 期望LOS角/(°)拦截时间/s脱靶量/mLOS角误差/(°)aME/(m·s-2)2017.22810.02150.0279102.47453015.69770.02370.028080.18184017.38880.01640.0209137.5841 1) 设计了一种自适应终端滑模制导律,能够实现对机动目标的精确打击和终端角度约束的要求。自适应估计的结构简单,不影响制导系统的有限时间稳定性,提高了系统的抗干扰能力。 2) 设计的滑模面通过巧妙地构造一个包含制导系统状态变量的混合项,解决了现有终端滑模制导律在处理奇异性时面临的滑模面不能严格收敛以及系统状态最终无法收敛到零的问题,提高了制导性能。 3) 所设计的制导律提高了制导系统的收敛速率和终端角度约束的精度,通过与ANTSMG以及ANFTSMG在相同场景下仿真对比,验证了本文所设计的制导律的优越性。


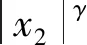




2.2 制导律设计







3 仿真分析



3.1 仿真对比




















3.2 以不同的初始航迹角γM0拦截目标



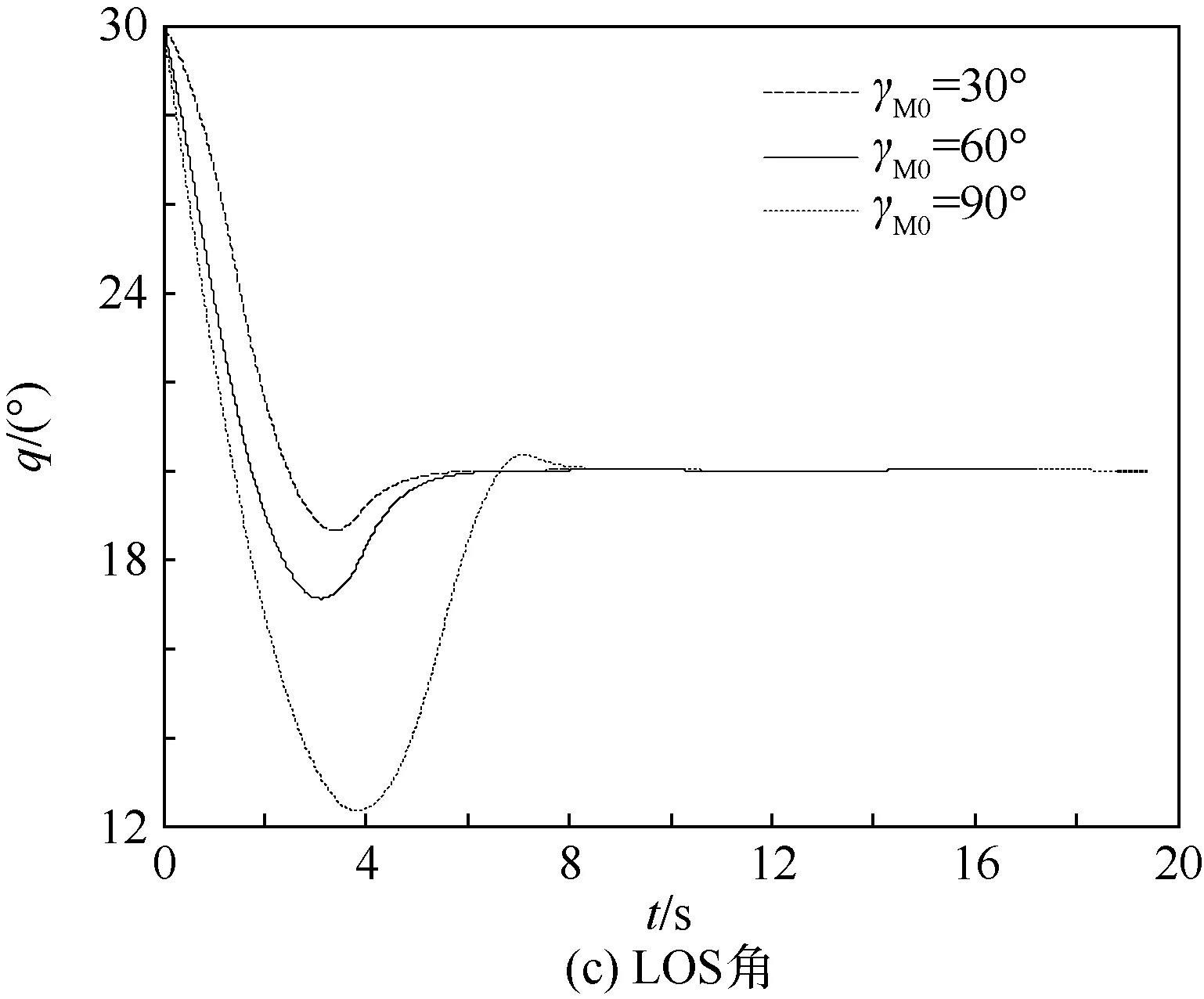



3.3 以不同的期望终端LOS角qd拦截目标







4 结 论
