插装式二维(2D)伺服阀的理论分析与实验研究
2019-05-25何晋飞陈烜鲁鹏勇阮健常亮
何晋飞,陈烜,鲁鹏勇,阮健,*,常亮,2
1. 浙江工业大学 机械工程学院,杭州 310014 2. 浙江交通职业技术学院,杭州 311112
插装阀相对于其他连接方式的液压阀,具有许多不可取代的优点,如密封可靠、重量轻、易于系统集成、加工改型相对容易等[1],因此它是液压技术一个重要的发展方向。插装阀主要有盖板式插装阀和螺纹插装阀[2-3]。盖板式插装阀由插装件和控制盖板组成,一般作为二通阀使用,但是想要实现传统滑阀的三位四通功能,则至少需要4个二通插装阀组合使用[4],结构复杂,质量、体积也会相应变大。螺纹插装阀利用螺纹,将插装元件旋入集成块的安装孔,来实现其功能。凭借其拆卸组装方便、集成度高和适合批量生产等优点[5-7],被逐渐应用于重工机械、钻井平台、废料处理机械、林业设备和挖掘机等行业[8-11]。目前电液式螺纹插装阀一般是由电磁铁直接控制的直动式比例阀,其动静态特性水平会受到一定抑制,而且其流量往往会受到电磁线圈的功率和液动力的限制[12]。为了改进电控模块,Ouyang等[13]研究了插装阀的压电驱动机构,使用由金属磁致伸缩材料制造的螺杆来驱动插装阀,使得插装阀重量更轻。
伺服阀作为电液伺服系统的核心,能直接影响电液伺服系统性能,因此人们对于伺服阀的改进也在不断进行[14]。喷嘴-挡板伺服阀一般采用动态响应良好的喷嘴挡板阀作为导阀再加一级滑阀作为主阀的方式,导阀和主阀之间采用反馈杆实现级间反馈[15],具有灵敏度高,静动态性能好等优点。人们一般通过优化电-机械转化器来提高喷嘴-挡板阀的性能,如浙江大学的王传礼教授利用超磁致伸缩材料改进电-机械转换器,其实验表明该阀的阶跃响应时间为1 ms左右[16]。射流管阀利用射流管和接收器来代替喷嘴挡板,在抗污染能力上有所提高。但是两者在结构上均为导控级和功率级平行放置,与插装阀元件轴向排列的特点冲突,无法实现插装,功重比也无法进一步提高。直驱式电液伺服阀舍弃喷嘴挡板或射流管等易污染的元件,采用马达直接驱动阀芯运动,并通过LVDT (Linear Variable Differential Transformer)反馈形成闭环控制。该阀结构简单,抗污染能力强,但是流量也会受到电磁线圈的功率和液动力的限制。
浙江工业大学Ruan等[17]提出的二维(2D)伺服阀利用伺服螺旋机构[18]将阀套与阀芯有机组合,使得阀芯既有先导控制又能进行功率放大。所以2D伺服阀功重比高,体积小,重量仅为常规二级伺服阀的1/3,导控级泄漏小,还具有很好的抗污染能力,适用于航天航空等对功率密度要求高的工作场合[19]。由于2D阀芯一体化的结构特点,即先导级和功率级集成在单个具有双自由度的阀芯上,力矩马达与阀芯同轴连接,并安装在阀芯末端,可以进行插装结构设计。而且2D伺服阀力矩马达的输出力只用来克服阀芯转动的摩擦力及其惯性力,而不是液动力。
液压控制元件的发展趋势为质量轻、精度高、高压大流量、抗污染能力强和泄漏低等。针对传统伺服阀无法插装化,以及传统螺纹插装阀流量受到电磁线圈功率和液动力的限制,鲁鹏勇等[20]提出了插装式二维(2D)伺服阀,并对其进行阀套的流道仿真分析。而本文在其基础上,详细介绍该阀的具体结构,建立该阀的数学模型进行理论分析,最后对该阀的实物进行实验研究。
1 插装式2D伺服阀的介绍
插装式2D伺服阀主要由电-机械转换器模块、阀体模块和位置传感器模块组成。其结构如图1所示。其中P为高压口,T为低压口,A、B为工作口。
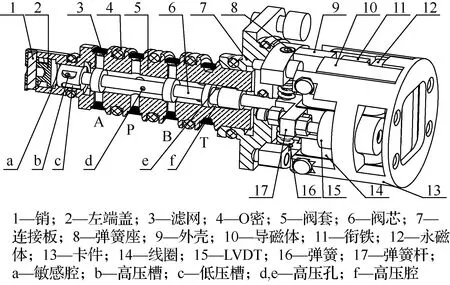
图1 插装式2D伺服阀Fig.1 2D cartridge servo valves
1.1 电-机械转换器模块
从硬件构成看,电-机械转换器是伺服阀的核心元件,其特性将在很大程度上决定了伺服阀的动态性能[21]。性能优异的电-机械转换器应具有小惯量大推力、响应快、磁滞小和线性度好等特点。
以往2D伺服阀的电-机械转换器采用的是一个带角位移反馈的步进电机,但是需要机械传动机构来传递和放大步进电机的输出力矩,结构上就不利于实现插装。因此设计了一种干式的力矩马达作为插装式2D伺服阀的电-机械转换器,省去了中间的机械传动机构,直接驱动阀芯运动,结构上更加简单。
动铁式力矩马达的衔铁惯量小、支撑弹簧管刚度大,所以比动圈式力矩马达的动态响应快。但是在大角度情况下,动铁式力矩马达非线性较差,而插装式2D伺服阀单边角度需求小于1°,在此条件下动铁式力矩马达的线性度能够满足需求。所以采用动铁式力矩马达。
如图2所示,力矩马达包括磁路组件和弹簧组件。磁路组件用来提供动力,输出转矩,由2个线圈、2个导磁体、1个衔铁和2个永磁体组成。衔铁采用软磁合金1J22,永磁体为高性能的钕铁硼Ndfeb52。导磁体材料与衔铁一致,两个导磁体分别布置于永磁体上下两侧,并与衔铁之间形成四个独立的工作气隙。控制线圈附在导磁体上,采用双余度设计,保证在其中一组控制线圈失效时,备份的一组能够保证力矩马达处于正常工作状态。弹簧组件用来提供约束力矩,调节输出,主要由1个弹簧座、2个弹簧和2个弹簧管构成。弹簧一端与弹簧杆相连,另一端与弹簧座相连,而弹簧座通过螺纹固定在外壳上,保证力矩马达在未上电时始终处于零位,在失电时能及时回复零位。而且弹簧座与外壳的螺纹连接是可调节的,即两侧的弹簧对称性不好时,可以调节弹簧座的螺钉来实现对称的目的。
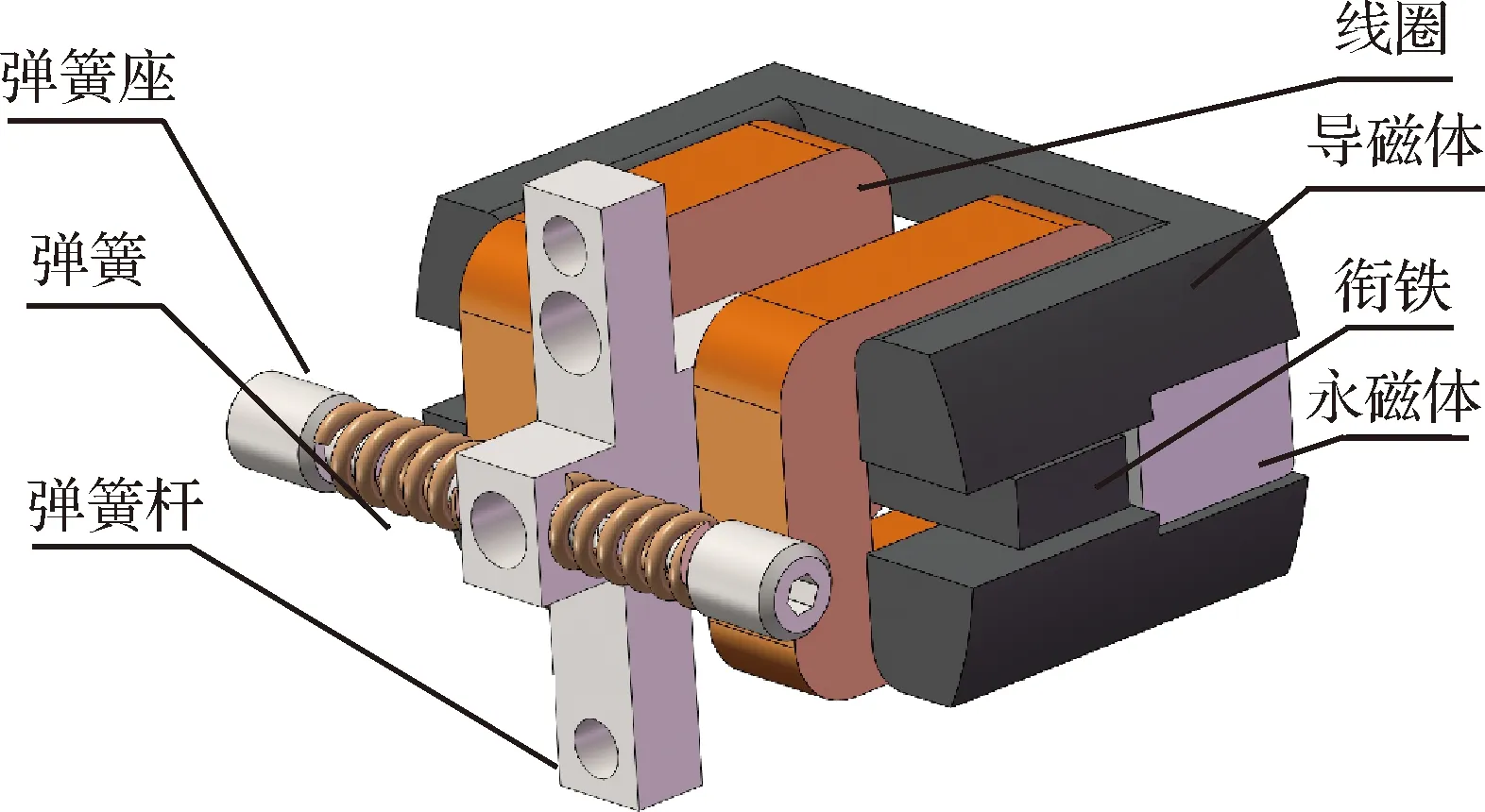
图2 力矩马达的结构Fig.2 Structure of torque motor
力矩马达的工作原理如图3所示。当控制线圈未输入电流时,力矩马达在其两端永磁体所形成的对称磁场下,输出力矩为零,衔铁在弹簧组件的作用下处于零位;当控制线圈通入电流时,力矩马达在永磁铁产生的永磁磁场和控制线圈所产生的控制磁场的差动作用下输出力矩,驱动衔铁转动,再加上弹簧组件产生的约束力矩,两者平衡时,衔铁终止扭转;当失电时,弹簧组件又使衔铁回到零点。
与传统力矩马达的弹簧管不同,弹簧组件的结构简单很多,因此加工更简单,成本更低。更为重要的是弹簧和2D阀的阀芯一样具有双自由度的特性,一方面衔铁带动弹簧杆转动,另一方面阀芯带动弹簧杆直动,而弹簧杆的转动和直动分别导致弹簧在阀芯径向和轴向扭转。其设计要求为当在弹簧杆端面施加20 N的水平直动力时,弹簧杆(即阀芯)的水平位移达到0.5 mm;当相同位置施加0.05 N·m的扭矩时,弹簧杆(即阀芯)的转角达到1°。
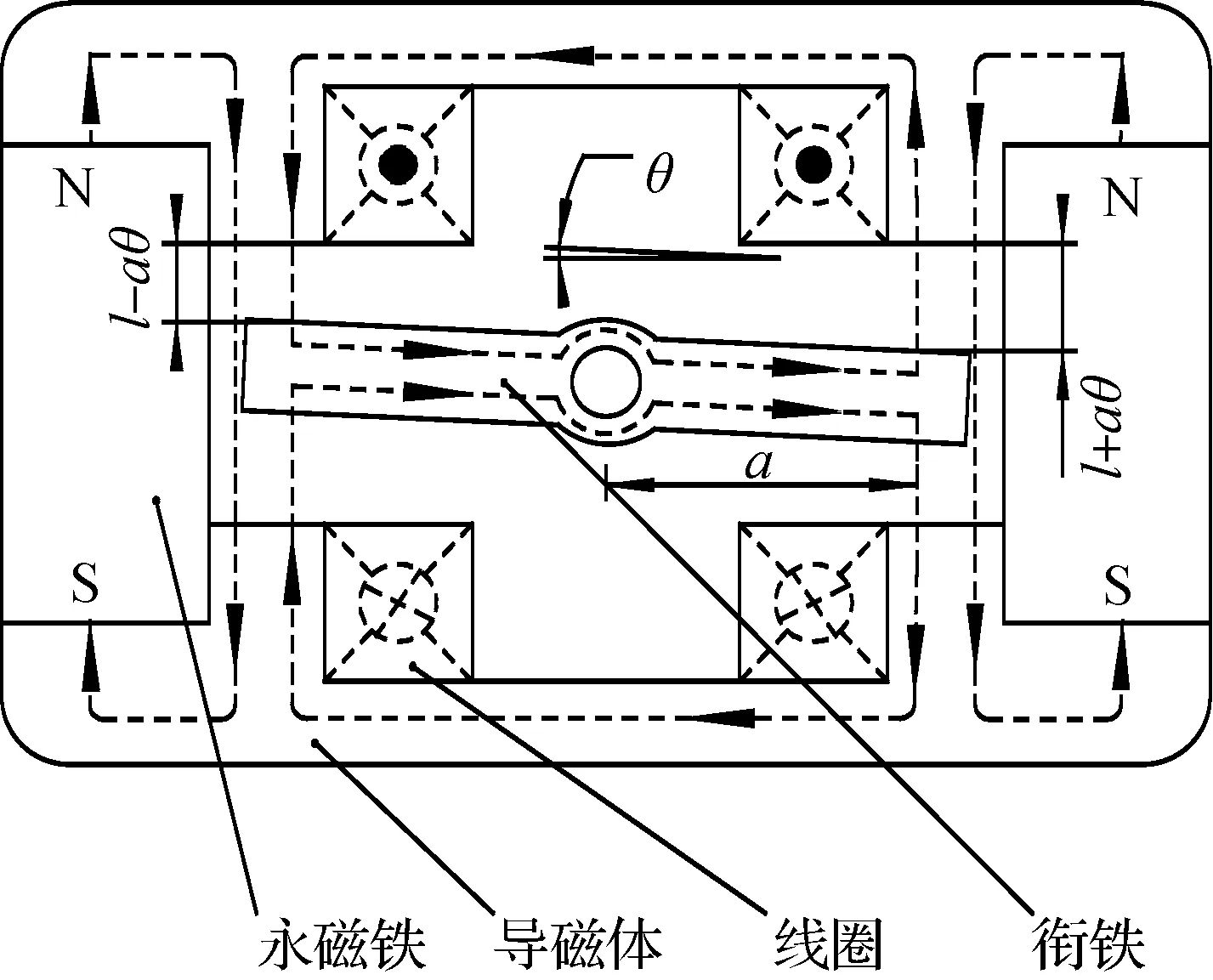
图3 力矩马达的工作原理图Fig.3 Working principle diagram of torque motor
因此,对弹簧组件进行力学仿真,以寻求合适的尺寸来满足弹簧的力学性能。其中弹簧的材料为50GrVA弹簧钢。在仿真过程中,将两个弹簧座固定约束,然后分别在弹簧杆上施加力和力矩,其结果如图4所示。在图4(a)中,当施加20 N的力时,弹簧座的最大位移为0.47 mm,基本满足需求;在图4(b)中,当施加0.05 N·m的力矩时,弹簧座最大位移为0.25 mm,角位移为1.1°,也基本满足要求。弹簧的具体参数参见表1。
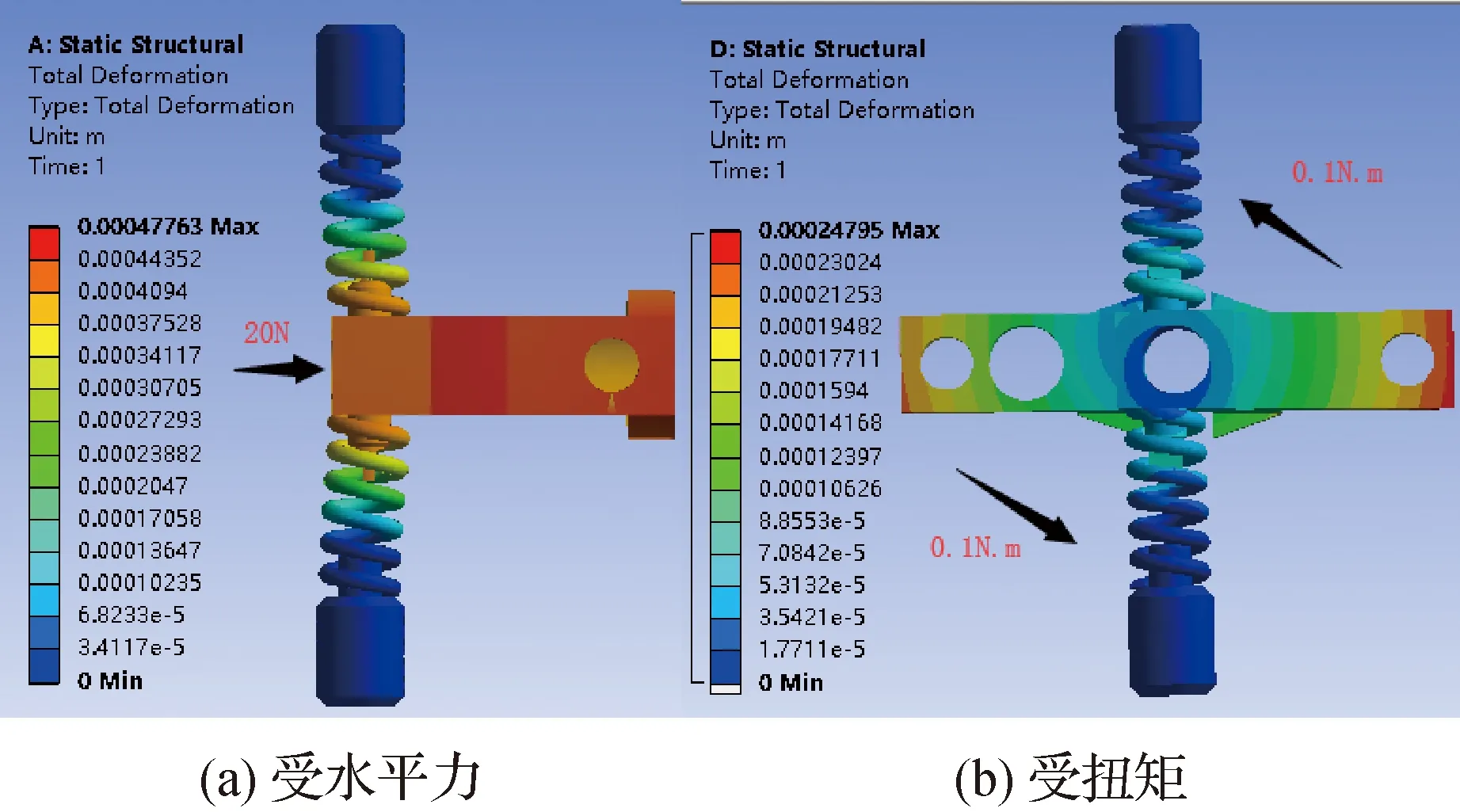
图4 弹簧组件的力学仿真Fig.4 Mechanical simulation of spring component
表1 弹簧的部分参数Table 1 Partial parameters of the spring
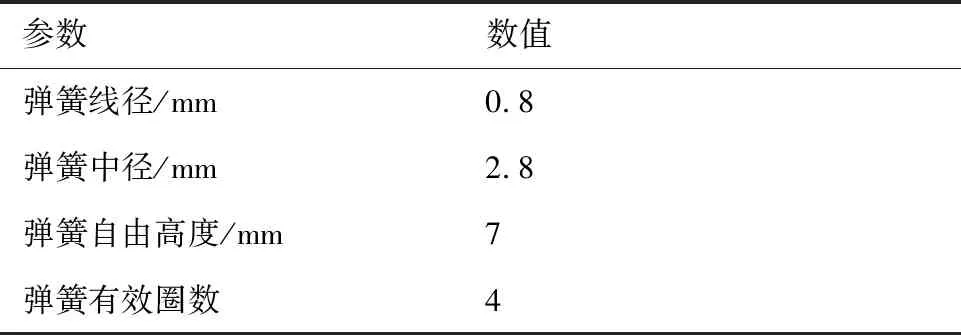
参数数值弹簧线径/mm0.8弹簧中径/mm2.8弹簧自由高度/mm7弹簧有效圈数4
线性度好的力矩马达的输出力矩为
Td=KtΔi+Kmθ
(1)
(2)
(3)
式中:a为从转角中心到气隙中心的距离在垂直于作用力方向的投影;l为衔铁在中位时工作气隙的长度(在图3标注);Nc为线圈匝数;φg为永磁体产生的固定磁通;Rg为气隙的磁阻;Δi为两个控制线圈的差动电流;θ为衔铁的转动角度;Kt为力矩马达的力矩常数;Km为力矩马达的磁弹簧刚度。
由式(1)可知,当力矩马达的力矩常数以及磁弹簧刚度恒定时,衔铁上输出力矩的大小仅与衔铁的转动角度和控制线圈的差动电流有关。
当衔铁发生偏转时,弹簧组件提供的约束力矩为
Tc=Kaθ
(4)
式中:Ka为衔铁转轴的机械扭转弹簧刚度。
利用式(1)和式(4),可以对力矩马达的静态特性进行分析。在空载情况下,力矩马达形成的输出力矩Td和弹簧杆产生的约束力矩Tc平衡,即可得力矩马达空载静态的角位移表达式:
(5)
式中:K为力矩马达的静态刚度系数。
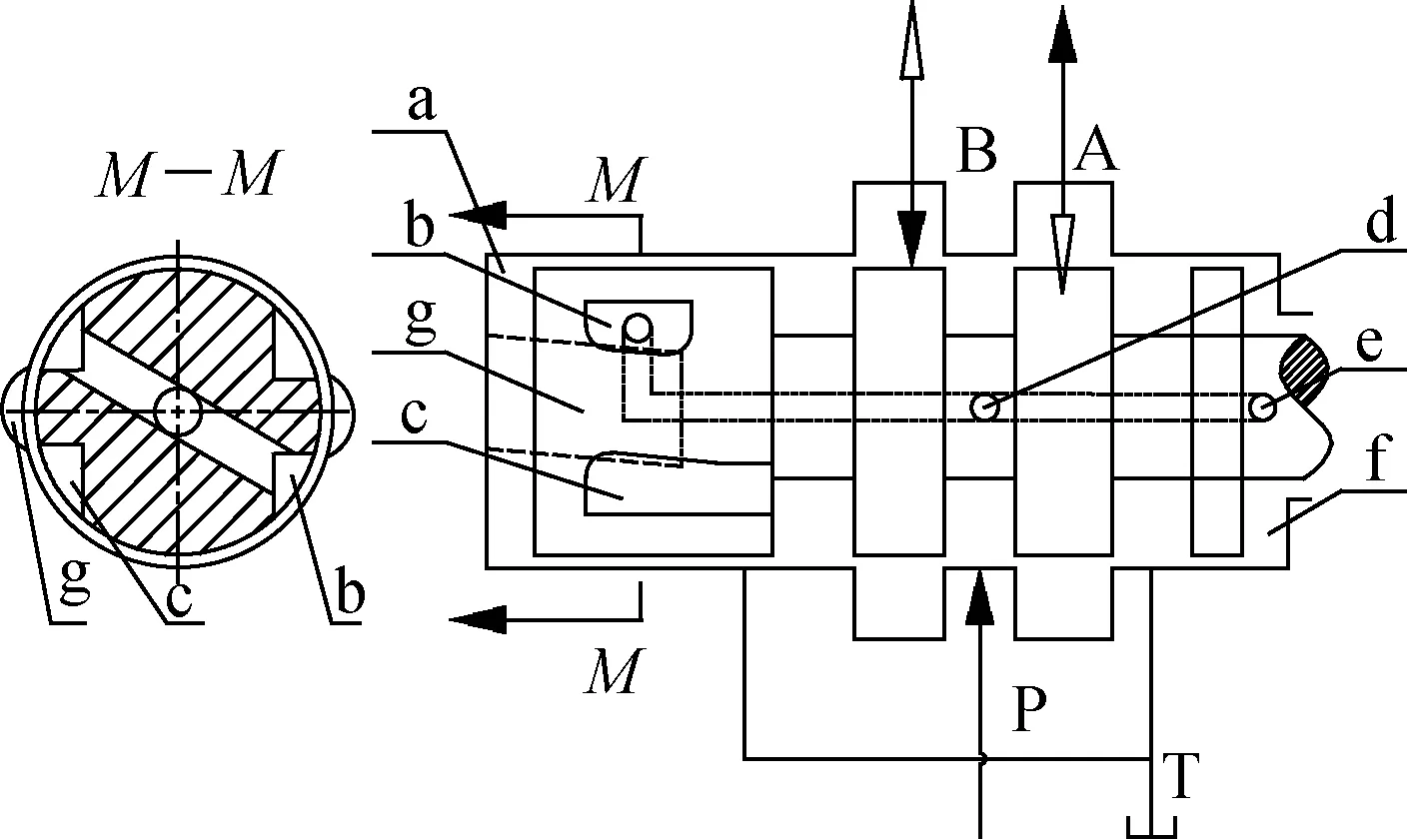
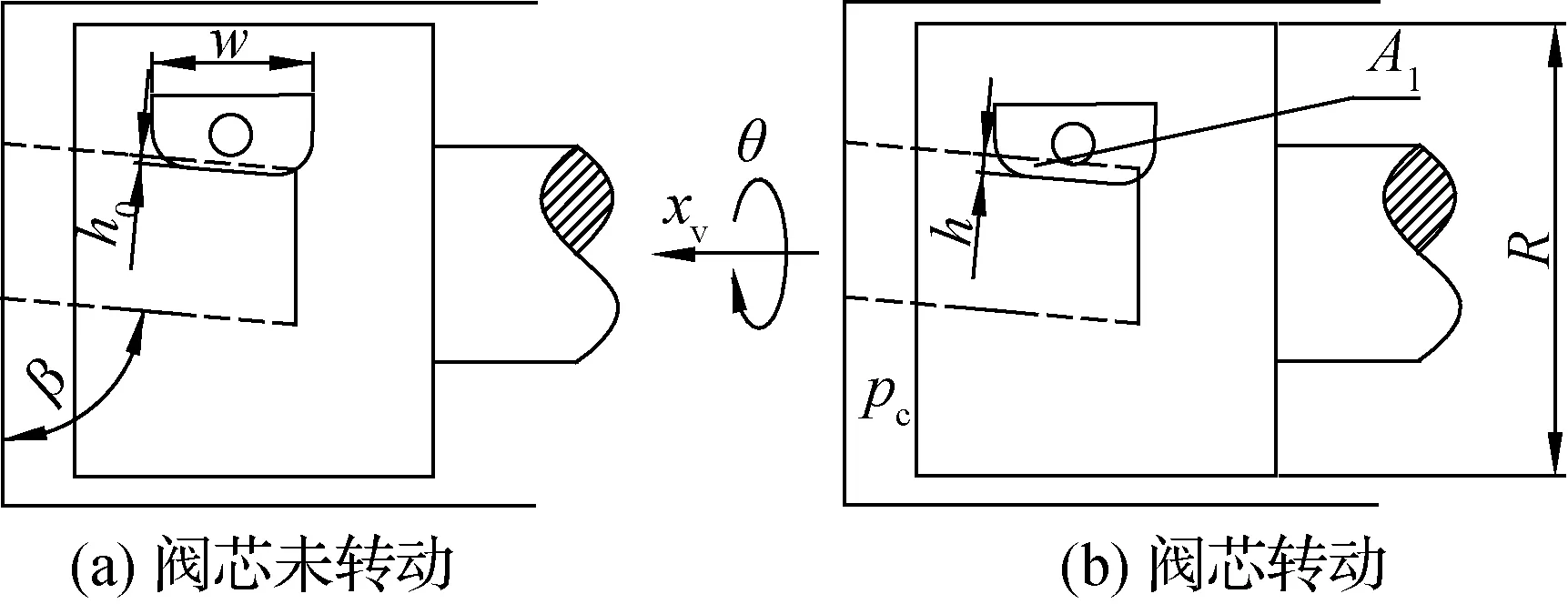
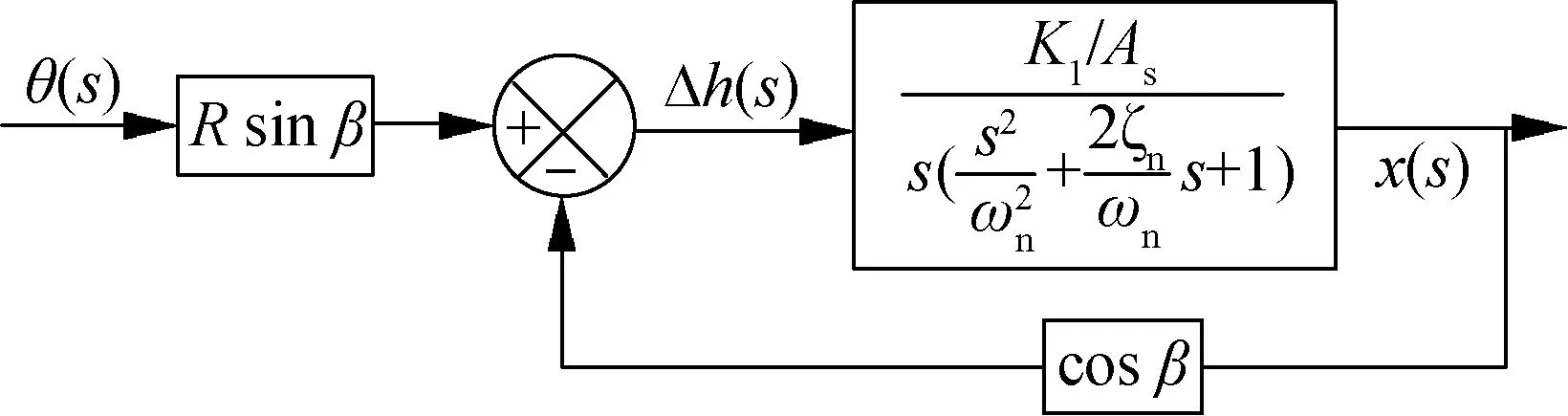
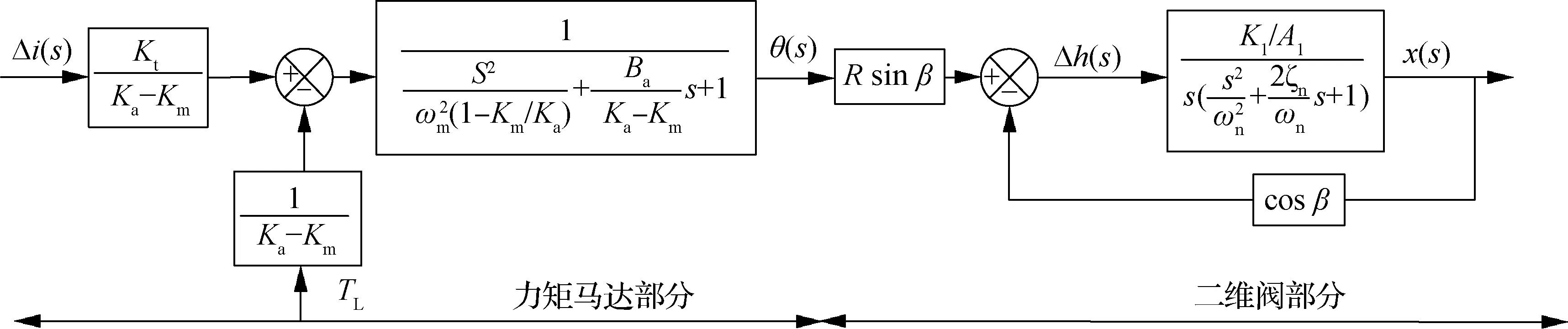
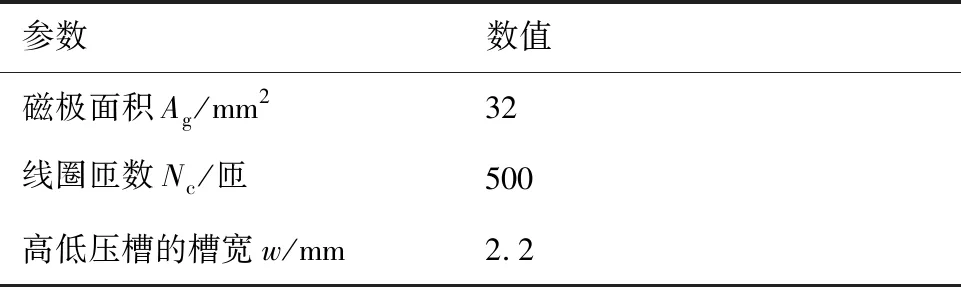
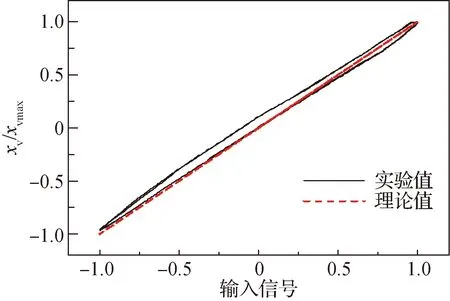
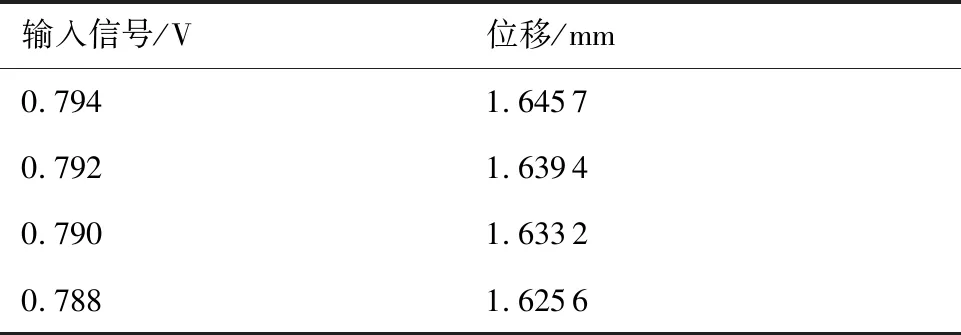
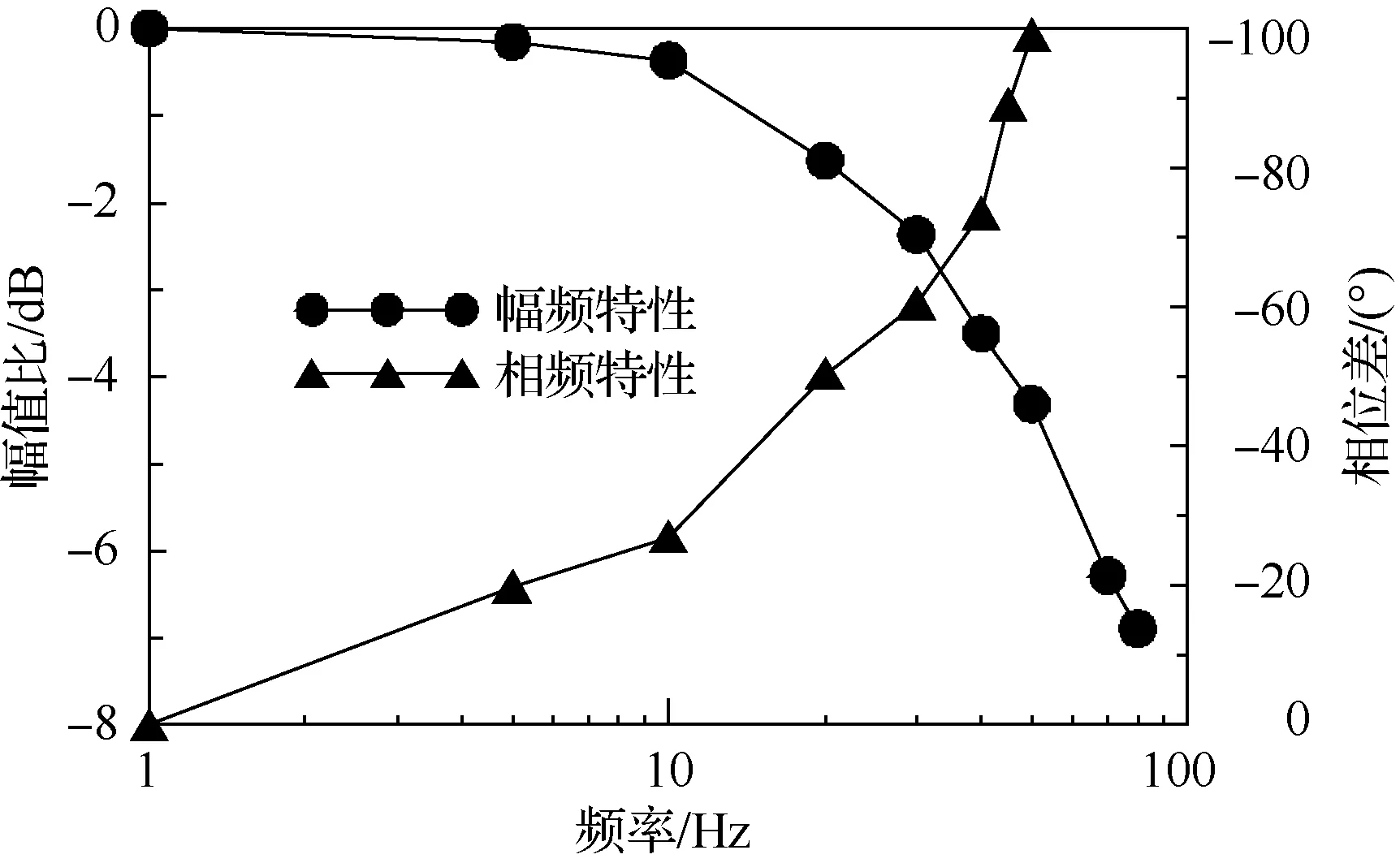
由式(5)可知,当Km 衔铁力矩平衡方程 (6) 式中:Ja为衔铁及任何加于其上的负载转动惯量;Ba为衔铁的机械支撑和负载的黏性系数;TL为作用在衔铁上的负载力矩。 将式(1)和式(6)合并后拉普拉斯变换得 KtΔi=Jas2θ+Basθ+(Ka-Km)θ+TL (7) 由式(7)可得,以差动电流和负载力矩为输入,转角为输出的系统方块图如图5所示。由图5 可得力矩马达传递函数为 (8) (9) 式中:ωm为衔铁的固有频率。 图5 力矩马达的控制框图Fig.5 Control block diagram of torque motor 阀体模块主要有阀芯、阀套、左端盖、销、O密和滤网等组成。如图6所示,阀芯左端与左端盖构成敏感腔a;高压槽b和低压槽c通过阀套上的斜槽g与腔a沟通;a腔压力由高压槽b和低压槽e与斜槽g相交的两个微小弓形面积串联的液压阻力半桥控制;槽b和高压孔d、e通过阀芯内孔相通;e使其所在的腔室形成高压腔f。阀芯旋转改变弓形面积,影响腔a的压力;a、f两腔的压力差导致阀芯的直线位移;阀芯的直线位移也会改变弓形面积,影响腔a的压力,最终平衡。当衔铁带动阀芯逆时针转动(从阀体看往力矩马达的方向)过程中,低压槽c与斜槽的重叠面积变大,高压槽b与斜槽的重叠面积减小,导致左侧敏感腔a压力下降,而右侧的高压腔f压力不变,从而使得阀芯向敏感腔体积减小的方向运动。在运动过程中高压槽和低压槽与斜槽的相交面积发生与前述相反的情况,敏感腔的压力逐渐增大,最终使得阀芯回到平衡位置。此过程体现了伺服螺旋机构的特性:较小的电磁输出力矩通过伺服螺旋机构进行功率放大,可以转化为较大的液动力(两腔的压力差),从而推动阀芯直动,同时还具有反馈功能。 图6 2D阀的结构原理Fig.6 Structure principle of 2D valve 衔铁输出转角θ,阀芯与衔铁固连,因此阀芯转角也为θ。从左往右看顺时针为正。如图7所示,高压槽与斜槽的重叠高度为 h=Rθsinβ+h0 (10) 式中:R为阀芯半径;θ为阀芯旋转角位移;h0为阀芯零位时高低压槽与斜槽的初始重叠高度;β为斜槽倾斜角度,取87°。 图7 2D阀先导控制示意图Fig.7 Pilot control schematic diagram of 2D valve 高压槽与低压槽和斜槽之间的相交面积越大,导控流量越大,阀芯的动态响应越快。为了加快响应,不采用传统的高低压孔方式,而是采用高低压槽的结构。因为该2D阀芯转角很小,高压槽的圆角半径也很小,因此可将交互面积近似成长度一定,高度随阀芯转角θ呈线性变化的平行四边形的面积。高压槽与斜槽的交互面积为 A1=Rθw+wh0/sinβ (11) 式中:w为高压槽的槽宽。 同理可得低压槽与斜槽的计算面积A2为 A2=-Rθw+wh0/sinβ (12) 所以高压槽流入敏感腔的流量q1为 (13) 式中:Cd为流量系数,取0.62;ps为系统压力,pc为敏感腔压力;ρ为油液密度。 由敏感腔经过低压槽流出的流量q2为 (14) 如果不计阀芯和阀套之间的间隙泄漏,假设油液不可压缩,流量的连续性方程为 (15) 式中:As为敏感腔对阀芯的作用面积;βe为体积弹性模量;x为阀芯位移;Vc为敏感腔容积。 阀芯动力学方程为 (16) 式中:Ar为高压腔对阀芯的作用面积;m为折算到阀芯上的总质量;Bp为作用在阀芯上的总黏性系数;FL为外部负载的总作用力;KL为负载的弹簧刚度。 伺服螺旋机构存在反馈环节,其轴向位移x、角位移θ和重叠高度变化量Δh之间的关系为 Δh=Rθsinβ-xcosβ (17) 式(10)~式(17)构成了阀体模块动态特性的支配方程。不考虑系统非线性因素,据此可得图8 所示的方块图。然后得其传递函数为 (18) (19) (20) (21) (22) 式中:ωn为液压固有频率;ζn为液压阻尼比。 通过位移可以进一步求得滑阀流量,根据流量公式可得阀芯位移与滑阀流量的关系为 (23) 式中:Q为阀口流量;ω为阀口通流面积梯度;Δp为阀口单边压降。 图8 伺服螺旋机构的控制框图Fig.8 Control block diagram of servo screw mechanism 差动变压器式位移传感器是基于LVDT原理进行非接触式位移测量,具有结构简单、精度高等优点,被大量应用于航天航空、机械等领域[22]。位移传感器采用LVDT CD375-025型号。LVDT传感器与外壳和卡件的圆弧配合,通过螺纹使卡件压死LVDT传感器。弹簧杆与LVDT连接杆通过螺纹连接,并通过外六角来保证两者的垂直度。LVDT传感器内部设有铁芯,连接杆与铁芯螺纹连接,铁芯可在传感器内直动。在力矩马达工作过程中,衔铁带动弹簧杆及阀芯转动,结合伺服螺旋原理,阀芯还作直线运动,同时带动弹簧杆与铁芯直动,铁芯位移将以电信号的形式传递给控制器,从而实现阀芯位移的闭环控制。 此模块的设置只是为了提高插装式2D伺服阀的性能(动静态等),适用于性能要求很高的地方。然而在某些性能要求不是很高的场所(滞环小于5.5%,动态频响不低于30 Hz),该阀不采用此模块也可以满足需求。 根据上述分析,且不考虑LVDT反馈,可以得到插装式2D伺服阀开环控制系统框图,如图9所示。系统以差动电流Δi和作用在力矩马达上的负载力矩TL(即衔铁带动阀芯转动时的负载力矩)为输入,阀芯位移为输出的开环传递函数如式(24) 所示。通过整个系统的传递函数,可以进行仿真研究具体参数对系统输入输出的影响及稳定性。 图9 插装式2D伺服阀控制方块图Fig.9 Control block diagram of 2D cartridge servo valves (24) 插装式二维(2D)伺服阀的仿真主要是根据上述的动态性能的支配方程,研究力矩马达的差动电流Δi(输入)阶跃变化时,力矩马达的磁极面积Ag、线圈匝数Nc和高低压槽的槽宽w对阀芯的轴向位移xv(输出)的影响。仿真的部分参数如表2所示,仿真结果见图10。 表2 仿真的部分参数Table 2 Partial parameters of simulation 图10 关键参数对阶跃响应的影响Fig.10 Effects of key parameters on valve’s dynamic characteristics 从图10(a)可以看出,随着磁极面积的增大,阶跃响应时间反而增大。这是因为虽然磁极面积变大会加快阀芯的响应速度,但是也会增加其位移的稳态值,从而导致阶跃时间增加。 从图10(b)可以看出,随着线圈匝数的增加,阶跃响应的时间不会发生变化,而且随着线圈匝数的增加,阀芯位移成比例增加。这是因为线圈匝数在整个系统充当的角色相当于一个放大系数,对响应时间无影响。 从图10(c)可以看出,高低压槽的槽宽的改变不会影响阀芯位移的稳态值。但是随着槽宽的增加,响应时间会略微减少,这是因为增大槽宽会增加其流量增益,响应速度变快,但同时也会导致泄漏变大。 同时还可以看出,插装式2D伺服阀的阶跃响应没有超调,表现出过阻尼的阶跃响应特性,这说明插装式2D伺服阀是一个过阻尼系统,稳定性很好。 结合设计要求,最终设计的插装式2D伺服阀尺寸为38 mm×38 mm×89 mm,质量为155 g,流量为12.6 L/min。实物如图11所示,安装如图12所示。 图11 插装式2D伺服阀实物图Fig.11 Photos of 2D cartridge servo valve 图12 插装式2D伺服阀实验工装Fig.12 Installation of 2D cartridge servo valve 实验测试平台的原理框图如图13所示。测试系统主要包含信号发生器、示波器、插装式2D伺服阀、流量计、液压泵站、激光位移传感器等。实验地点为浙江工业大学二维(2D)液压气动工程研究中心。 改变截止阀可以实现不同的系统功能,即不同的测试工况。信号发生器产生不同的输入曲线,激光位移传感器直观的显示阀芯位移变化。结合设计要求,本次实验主要测量该阀在开环情况下的动静态特性、分辨率以及阶跃相应。在开环情况下,LVDT信号(型号为CD375,量程为±0.63 mm)作为样机的输出信号。图14即为实验测试图。(实验系统压力10 MPa,室温20°) 图13 实验系统原理图Fig.13 Schematic diagram of experimental system 图14 插装式2D伺服阀实验台Fig.14 Experiment table of 2D cartridge servo valve 3.3.1 开环下的伺服阀静态特性 图15为插装式2D伺服阀的开环静态测试曲线,其实验条件为:截止阀7、8、9打开,系统压力10 MPa、b口通过流量计相连,此时流量计可以当静态的液压缸,伺服阀满量程输入,即±0.3 mm 的阀芯位移(由于流量配磨的限制,现在只能通过位移曲线替代流量曲线,±0.3 mm的位移对应的流量大小为12.6 L/min)。信号发生器给出的输入信号为电压信号,频率为0.02 Hz,曲线样式为正弦波,输出信号为阀芯的位移信号。 图15 静态曲线Fig.15 Static curve 由曲线得知:开环情况下滞环大小为5%,线性度均满足指标。这是因为螺旋伺服机构本身具有反馈功能,所以在开环的情况下也能保持良好的滞环和线性度。理论的开环曲线优于实验的结果,是因为没有考虑到力矩马达的滞环,同时在建立传递函数时将一些参数进行线性化分析。 3.3.2 开环下的分辨率实验 分辨率是使伺服阀的流量发生变化(增大或减少)的输入电流的最小增量。本次测量方法为:在10%的输入信号处停止,缓慢减小电流,读取位移变化。 伺服阀测试的输入信号为电压信号,大小为0.6~1.0 V,选0.794 V时,阀芯位移为1.645 7 mm,缓慢减小输入信号值,得出位移与输入信号的对应关系,如表3所示,开环下的分辨率≤1%。 表3 分辨率实验结果Table 3 Experimental results of resolution 3.3.3 开环下的阶跃响应 阶跃响应曲线指伺服阀零位到单边最大开口时,流量(位移)曲线随输入信号(电压信号)的响应时间。图16即为开环响应曲线。满量程输入,系统压力10 MPa,室温20°。 图16 阶跃响应曲线Fig.16 Step response curve 插装式2D伺服阀阶跃响应的实验结果表现为过阻尼,且无超调,这与仿真结果一致。实验开环响应时间为10 ms,而仿真结果约为8 ms,这可能是没有考虑到力矩马达滞环的影响。而一般伺服阀的响应时间大概为20~40 ms之间,相比之下插装式2D伺服阀的响应速度非常快,这主要是因为采用了2D阀的结构,同时有一些系统的优化如马达采用动铁式,伺服螺旋机构将高低压孔改成高低压槽等。 3.3.4 开环下的动态特性 动态特性表征输出信号随输入信号的跟随能力。本次实验中,信号发生器给出不同频率的满量程正弦波输入信号,得到多组输出信号(位移信号)与输入信号(电压信号)的正弦波跟随曲线。结合动态频响的定义,以1 Hz作为幅频与相频的基准信号,将动态特性曲线整理如图17所示。截止阀9打开,满量程输入,系统压力10 MPa,室温20°。 由图17得插装式2D伺服阀的幅频(-3 dB)约为35 Hz,相频(-90 °)约为45 Hz。即在满量程输入时,插装式2D伺服阀的开环动态频响为35 Hz。 图17 动态特性Fig.17 Dynamic characteristics 插装式2D伺服阀的实验数据如表4所示,开环下的性能已经能满足要求,而如果通过LVDT实现闭环控制,其性能还可以有很大的提高。因此,在正常情况下该阀开环即可,而在要求更高的场合可以采用闭环。 表4 实验数据整理Table 4 Data reduction of experiment 1) 本文研究的插装式2D伺服阀,通过力矩马达的偏转角度来直接驱动阀芯运动,进而控制伺服阀的输出流量,同时还可以通过LVDT检测阀芯位移实现位置闭环控制。 2) 插装式2D伺服阀相对于普通的插装阀结构更加简单,尺寸更小,重量更轻,响应快,控制精度高,同时抗污染能力强,在航空航天及军工领域有广阔的应用前景。 3) 力矩马达中的磁极面积增大反而会增加系统阶跃响应时间;力矩马达的线圈匝数充当比例放大系数的角色;2D阀的斜槽宽度增加会加速响应,同时不会放大输出,但是会增加泄漏。同时,该阀具有过阻尼特性,无超调,系统很稳定。 4) 实验表明,该阀具有良好的动静态特性:开环情况下滞环大小为5%,分辨率≤1%,线性度较好,响应时间为10 ms,动态频响为35 Hz。在闭环情况下性能还可以有很大提高。其动静态特性均满足设计要求。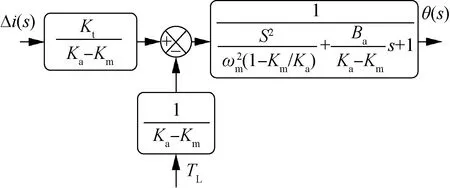
1.2 阀体模块
1.3 位置传感器模块
1.4 插装式二维(2D)伺服阀
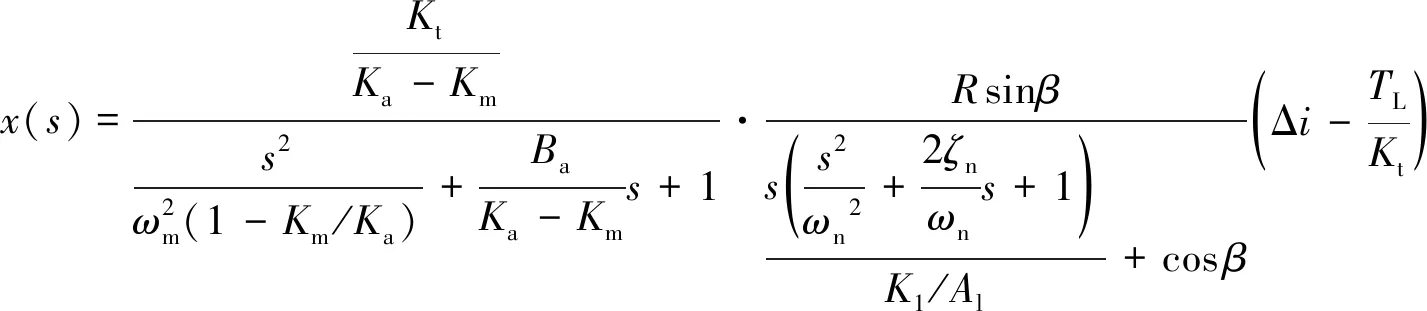
2 插装式2D伺服阀的仿真

3 实验研究
3.1 实物介绍


3.2 实验平台及原理
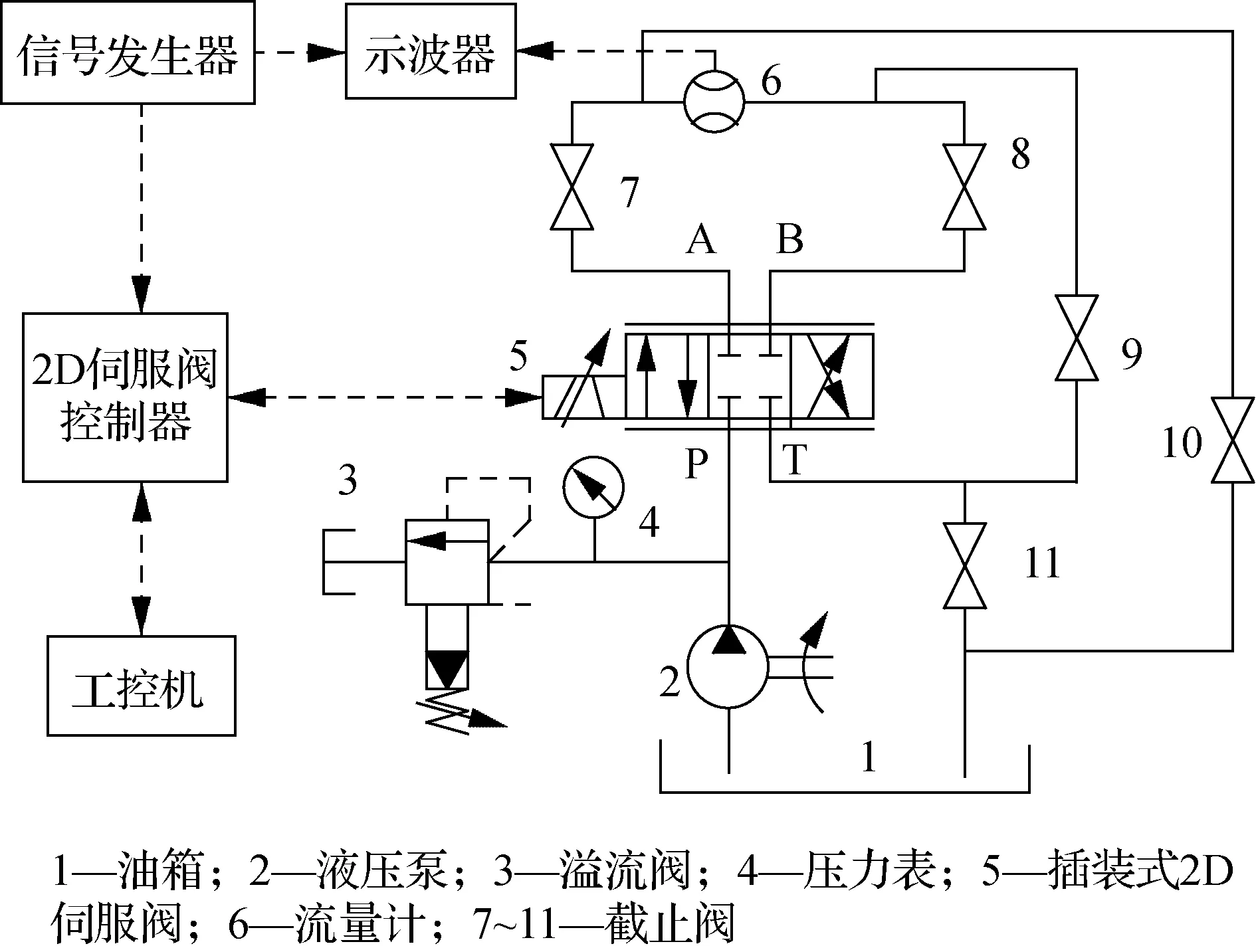

3.3 实验结果

3.4 性能参数整理

4 结 论
