基于虚拟慢时间的双基地ISAR成像算法

2019-05-25史林韩宁宋祥君王立兵崔东辉

航空学报 2019年5期

史林，韩宁，宋祥君，王立兵，崔东辉

1. 陆军工程大学石家庄校区电子与光学工程系，石家庄 050003 2. 中国人民解放军32181部队，石家庄 050003 3. 中国人民解放军63961部队，北京 100010 4. 中国人民解放军78616部队，成都 610214

双基地逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)是空间目标监视的一种重要手段，可实现目标的多姿态观测，当发射站靠前布置时还可增大成像系统作用距离。双基地ISAR具有良好的“四抗性能”[1]，且成像不受目标运动方向限制，已逐渐成为国内外的研究热点[2-8]。因双基地配置固有的“三大同步”问题，目前针对双基地ISAR的研究还处于较为开放的研究阶段。国内外对双基地ISAR的研究也主要集中在运动补偿[9-10]、成像平面确定[11-13]、三维干涉成像[14-16]以及方位定标[17-18]等方面。

因双基地雷达系统固有的“三大同步”问题，反向投影(Back Projection, BP)、极坐标格式算法(Polar Format Algorithm, PFA)等对双基地雷达的系统配置精度、目标坐标位置和同步时钟误差敏感的算法难以在双基地ISAR成像中应用。距离-多普勒(Range Doppler, RD)算法物理意义明确、对收发同步精度的要求较低，被广泛应用于双基地ISAR成像仿真及实测数据处理。目前，大部分针对双基地ISAR的研究都假定成像期间双基地角是恒定不变的，但在实际成像过程中，双基地角是个时变量，双基地角时变会造成二维ISAR成像在方位向的散焦，影响图像的聚焦度。针对此问题，文献[19]利用粒子群优化算法估计双基地角时变带来的高次项系数，然后构造补偿相位项，实现自聚焦，但该算法中使用的粒子群优化算法是一种智能优化算法，只能以一定的概率估计出最优补偿系数，算法无法保证每次都收敛到最优解。文献[20]将稀疏分解算法引入双基地ISAR成像的自聚焦过程中，基于冗余基的高分辨特性，估计出高次项的系数而后完成补偿。为了提高补偿系数的精度，需扩大冗余基的个数，使得该算法的运算量较大，且该算法的最终成像效果受算法正则参数的影响较大，正则参数选取不当可能会造成无法对目标进行成像。文献[21]研究了双基地ISAR成像系统中越分辨单元徙动带来的影响及相应的处理算法。该算法基于广义Keystone变换，消除越距离单元走动；基于最大图像对比度准则，估计等效旋转中心，进行越多普勒单元徙动校正；依据图像畸变角度，通过对距离单元内像素进行移位操作实现图像的畸变校正。文献[22]基于图像旋转相关度最大准则，提出了一种更为精确的双基地ISAR等效旋转中心估计算法。其采用与文献[21]相同的越多普勒单元徙动校正和图像畸变校正算法。文献[21-22]中均假定完全精确已知目标空间位置和对应的双基地角。实际系统中，此假定并不成立。利用先验信息得到的卫星位置信息，是有误差的。此误差会导致每个周期双基地角和累积转角均产生误差。若对应的误差值较大，会影响后续越多普勒单元徙动校正和图像畸变校正。需进一步考虑双基地角、累计转角存在误差时相应的处理算法。

针对以上问题，本文聚焦于双基地角时变下，实际成像系统中多普勒向散焦及图像畸变问题，提出一种基于虚拟慢时间采样消除高次项影响，而后通过非均匀傅里叶变换完成方位压缩得到目标二维ISAR像的新型成像算法。

1 双基地ISAR成像模型

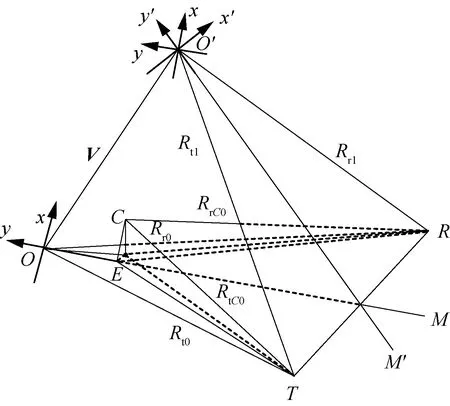
图1 双基地ISAR成像原理模型Fig.1 Imaging principle model for bisatic ISAR

本文以平稳空间目标为研究对象，其成像原理模型如图1所示。图中：T为发射站雷达；R为接收站雷达；TR为基线；L为长度为；Rt0、Rr0分别为观测起始时刻，目标相位中心距发射站和接收站的距离；Rt1、Rr1分别为目标运动到下一时刻，目标相位中心距发射站和接收站的距离；V为目标运动方向矢量；C为目标上的任一散射点；在观测起始时刻，散射点C在收发双站雷达和目标质心O确定的平面内的投影，记为E；RtC0、RrC0分别为散射点C在观测起始时刻，距发射站、接收站雷达的距离。

在观测起始时刻，以目标质心O为原点，建立惯性坐标系：在观测起始时刻，y轴正方向定义为目标双基地角平分线延长线方向；在目标双基地角平分线与目标轨道曲线构成的平面内，将y轴的法线定义为x轴，x轴正方向定义为目标运动方向。该坐标轴指向，不随目标的运动变化。此坐标系下，目标散射点距离的变化可分解为平动和相对转动两部分。O′由目标质心O移动得到。为便于分析目标转动情况，以O′为原点，建立以双基地角平分线延长线方向为y′轴的坐标系x′O′y′，该坐标系的y′轴随着双基地角平分线指向变化而改变；x′轴则是此刻目标双基地角平分线与目标轨道曲线构成的平面内y′轴的法向。因此，在观测时间内x′O′y′坐标系与xOy坐标系间的相对转动角反映了目标的相对转动情况。假定雷达发射的线性调频信号为

(1)

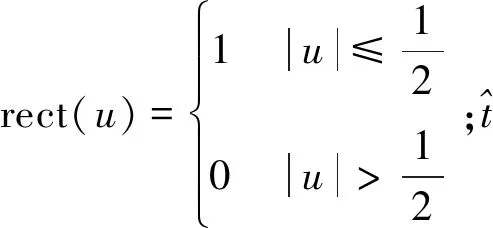
假双基地雷达理想同步，且成像期间双基地角恒定不变，在中频采样后通过数字下变频得到基频信号为

(2)

式中：σC为散射点C的散射系数；c为真空中的光速；R(tm)可表示为

RC(tm)=Rref(tm)+Rrot(tm)≈

(3)

式中：Rref(tm)为目标散射中心的平动分量；Rrot(tm)为散射点C的转动分量；θC为散射点C的方位矢量与xOy坐标系中x轴正向的夹角；ψ(tm)为成像期间双基地角平分线的转动角度；β为成像期间的双基地角。

结合式(2)和式(3)可以看出，双基地ISAR回波中散射点到收发双站的距离依然可以分解为平动项与转动项两部分。对式(2)进行脉冲压缩利用数字脉压完成距离维成像，而后进行运动补偿，在包络对齐之后，将平动和转动导致的相位项统一建模，进行相位补偿实现自聚焦，通过方位维压缩得到二维ISAR像[4,18]。

2 双基地角时变对ISAR成像的影响机理

在前文推导式(3)的过程中，假定了成像期间双基地角恒为β，当双基地角随慢时间变化时，式(3)可改写为

(4)

式中：β(tm)表示成像期间双基地角随慢时间tm变化。在较短的相干处理时间(Coherent Processing Interval，CPI)内，目标处于远场位置的条件下，双基地角随慢时间近似成线性变化，可以用一阶泰勒展开进行近似[4]

β(tm)=β0+Δβtm

(5)

式中：β0为零时刻的双基地角；Δβ为双基地角在零时刻的一阶导数。

将式(5)代入cos(β(tm)/2)进行展开，并忽略二次以上的高次项得到

K0+K1tm

(6)

式中：

(7)

(8)

在下文中，将K0、K1分别称为虚拟慢时间系数K0和虚拟慢时间系数K1。实际的双基地雷达系统中，收发双站的位置是固定的，可以根据收发双站的位置信息和目标的轨道信息，依据几何位置关系，获得双基地角信息，进而获得虚拟慢时间系数的值。

在较短的CPI时间内，平稳目标旋转一个微小的角度ψ(tm)=ωtm，ω为双基地角的平均转动角速度,此时sinψ(tm)和cosψ(tm)可近似为sinψ(tm)≈ωtm，cosψ(tm)≈1。对目标回波作平动补偿后，目标平动项被去除，目标依然可等效为转台目标。将式(6)代入式(4)中的目标转动项进行化简可得

ΔRC(tm)≈ 2(xiωtm+yi)(K0+K1tm)=

(9)

式中：(xi,yi)为散射点C在xOy坐标系中的坐标。

经过理想的运动补偿(包络对齐和初相校正)后，脉冲压缩后散射点的回波式(2)可表示为

(10)

将式(9)代入PC，可得

(11)

忽略常数项2yiK0，则第n个距离单元的对应的相位多项式信号为

(12)

式中：Ln为第n个距离单元内散射点的个数；i为第n个距离单元内散射点对应的下标。位于第n个距离单元内散射点的Ln个散射点的纵向距离(y1=y2=…=yLn)相等，因此，式(12)可以重写为

(13)

从式(13)可以看出，因成像期间双基地角随慢时间的变化，式中第1项将会引起图像畸变，且畸变量与距离坐标成正比，式中第2项导致成像所需的转动相位项出现了二次高阶项，若不对其进行补偿则会造成散射点方位向的散焦，进而会影响图像的聚焦度。

3 虚拟慢时间成像算法

3.1 初次相位补偿

为了消除图像畸变，同时为消除式(13)中高次项的影响，首先构建初次补偿相位项:

(14)

yn=(n-nc)Δy

(15)

式中：nc为等效旋转中心对应的纵向距离下标。因此，为构造初次相位补偿项φ1，需要确定散射点相对目标等效旋转中心的纵向定标距离yn、虚拟慢时间系数K0和虚拟慢时间系数K1。其中，虚拟慢时间系数可以通过双基地角得到。散射点纵向距离的定标量需要确定图像的等效旋转中心的纵向位置。等效旋转中心的位置的估计在3.4节进行分析。

已获得初次补偿相位φ1的基础上，将式(14)与式(13)相乘，完成初次相位补偿后可得

(16)

3.2 非均匀傅里叶变换实现方位压缩

完成初次相位补偿后，由于双基地角时变的影响，回波数据中包含与散射点方位向坐标有关的高次项。此时基于傅里叶变换进行方位压缩，将引起方位向散焦。为消除高次项的影响，可采用距离瞬时多普勒(Range Instantaneous Doppler, RID)成像算法，来提高成像质量。RID成像算法可分为两大类。第一类是基于时频分析的成像算法。基于Wigner-Ville分布(Wigner-Ville Distribution, WVD)类算法属于双线性变换，需要在时频聚集性和交叉项之间进行平衡。基于参数化的时频分布算法，如基于自适应线性调频分解类的算法，无交叉项影响，但运算量大，且对噪声和初值选择比较敏感，应用受限。另外一类是基于参数估计的高次相位补偿算法。该类算法通过分数阶傅里叶变换(Fractional Fourier Transform, FrFT)等参数估计算法，估计信号的高阶项系数，补偿高次相位的影响。但此类算法需要估计每个距离单元相位多项式信号的参数，运算量大，且成像效果依赖与参数估计的精度。空间目标脉冲压缩后回波信噪比低，参数估计精度不高，此类算法应用受限。

双基地ISAR成像期间，基于空间目标轨道的先验信息和成像几何关系，可获得相对精确的双基地角信息，进一步估计相应的时变信息。定义虚拟慢时间τm满足如下关系式:

(17)

定义式(17)为虚拟慢时间。将式(7)和式(8)代入式(17)可得每个慢时间tm对应的虚拟慢时间τm。将式(17)代入式(16)可得

(18)

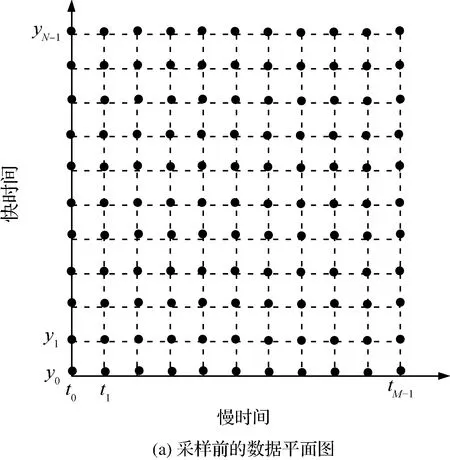
图2 虚拟慢时间采样前后的数据平面图Fig.2 Data plane before and after virtual slow time sampling

式(18)中相位项仅包含虚拟慢时间τm的一次项。利用式(17)对回波数据完成虚拟慢时间映射前后的数据平面如图2所示。图2(a)和图2(b)的横轴分别为慢时间和虚拟慢时间，纵轴均为快时间。对比图2(a)和图2(b)，回波数据完成虚拟慢时间映射后，相邻虚拟慢时间之间不再是固定不变的时间间隔。经过虚拟慢时间映射，去掉了慢时间二次项影响，等效对方位向回波实现了虚拟非均匀采样，可利用非均匀傅里叶变换完成方位压缩得到目标的二维ISAR像。

令τ=[τ0,τ1,…,τM-1]，则补偿系数矩阵的基可表示为

(19)

基于式(19)，构建用于方位压缩的补偿系数矩阵Ψ:

Ψ=[γ0,γ1,…,γM-1]

(20)

利用式(20)对初次相位补偿后的数据进行方位压缩，即可得到目标的二维ISAR像。由于非均匀傅里叶变换采用的不是完全正交的基函数，无法采用Cooley和Tukey算法[23]。若直接进行矩阵运算，计算虚拟非均匀采样信号sn(τm)与每一个频率样本点的相关值，需要4N次的实数加法和(4N-2)次的矩阵乘法。与N个频率点进行相关运算，总的运算量为O(N2)数量级。为了减少运算量，采用文献[24]中的Goertzel算法。这种算法总的计算量是(2N+4)次实数相乘和(4N-2)次实数相加，将运算复杂度降低到O(N)的数量级。若对W个距离单元进行方位压缩，计算量为O(WN)。

3.3 等效旋转中心估计

(21)

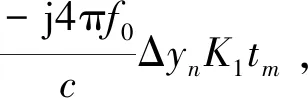
式中：C_imag为图像对比度；I(x,y)为复图像的幅度；A(I(x,y))为图像在整个成像平面上的幅度平均。首先假定等效旋转中心位置，并以此中心构造补偿相位项φ1，进行初次相位补偿后，进行虚拟慢时间采样、方位向非均匀方位压缩，得到ISAR二维像，计算图像对比度。然后，更换假定的等效旋转中心位置，重复以上步骤。当等效旋转中心位置是实际旋转中心时，图像对比度最大，图像聚焦效果最好。为了减小搜索范围，考虑到等效旋转中心位置一般与强散射点有关，因此，选择峰值较大的距离单元两侧进行搜索，既可以快速找到等效旋转中心，又减少了运算量。

3.4 虚拟慢时间系数参数估计

前文的分析中，假定根据目标的轨道信息和收发双站的位置的先验信息，精确获得双基地角的信息。实际的系统中，双基地角的估计值和真实值之间存在着一定的误差。因此，本节分析在双基地角存在估计误差的情况下的虚拟慢时间系数K0和K1参数估计算法和鲁棒性。

假定系统测量的双基地角为

(22)

(23)

(24)

3.5 算法流程

综合以上分析，本文提出的虚拟慢时间ISAR成像算法流程如图3所示。

图3 所提算法的成像流程Fig.3 Imaging process of proposed algorithm

在图3中用虚线框内内容为本文所提算法的关键步骤。具体步骤为

步骤1对双基地ISAR回波进行脉冲压缩、包络对齐、相位校正，得到平动校正后的一维距离像序列。

步骤3假定等效旋转中心位置，按照式(14) 和式(15)构造初次相位补偿项，补偿一维距离像。

步骤4按照式(17)进行虚拟慢时间采样，并完成非均匀傅里叶变换，得到ISAR图像，计算图像对比度。

步骤5假定新的等效旋转中心位置，重复步骤3和步骤4并将此次图像的对比度与上次的对比，若对比度变大，存储二维ISAR图像，如此循环，直到遍历完毕可能的等效旋转中心位置。

步骤6遍历结束，存储的即为图像对比度最大的二维ISAR图像，输出图像矩阵。

4 仿真实验

4.1 典型散射点目标成像结果分析

仿真双基地雷达参数及目标的初始轨道根数如表1和表2所示。积累脉冲数为512。回波基于文献[25]的算法模拟生成。通过收发双站及目标的位置信息和成像几何关系，获得双基地角和等效累积转角。

表1 仿真双基地雷达参数Table 1 Simulation parameters of bistatic radar

表2 初始轨道根数Table 2 Initial two line elements

图4给出了仿真用的目标三维和二维散射点模型。双基地角是双基地ISAR成像的重要参数，为此，给出了某一可见观测时间段内的双基地角变化曲线，如图5所示，并由此确定所选择的仿真成像弧段。从图中可以看出，在观测时间内，只有在曲线顶点附近的小部分时间内双基地角是非线性变化的(在基线的中心位置附近)，大多数时间内双基地角是线性变化的。选取特定的512个周期回波数据作为成像段数据，如图5中加粗线段所示，对应的积累时间为5.12 s。该观测时间内双基地角变化约为6.36°，放大后可看出，此期间双基地角与慢时间近似成线性关系。等效单基地雷达对应的成像累积转角随积累脉冲数的变化情况如图6所示。期间目标等效累积转角约为4.26°，并且累积转角与慢时间成线性关系。

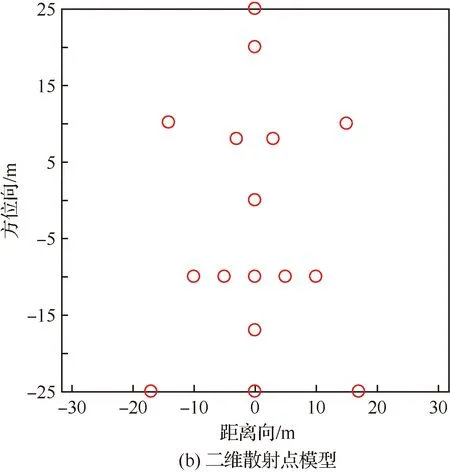
图4 三维和二维散射点模型Fig.4 Three-dimensinal and two-dimensinal scattering point model

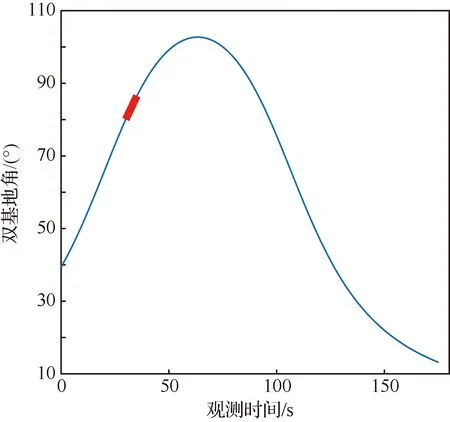
图5 双基地角随观测时间变化曲线Fig.5 Variation curve of bistatic angles with observation time

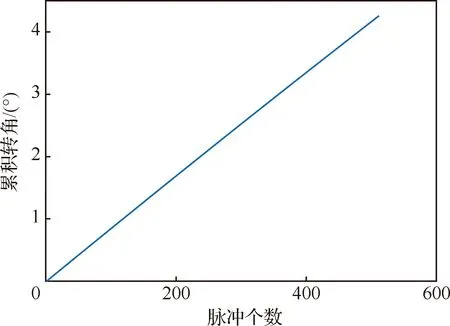
图6 目标等效累积转角随脉冲个数的变化曲线Fig.6 Variation curve of equivalent cumulative angle of target with pulse number

图7(a)和图7(b)为RD成像算法得到的二维ISAR像(基于最大互相关法完成包络对齐；利用相位梯度自聚焦(Phase Gradient Autofocusing，PGA)算法完成初相校正)。图7(a)为定标前的ISAR像，图7(b)为定标后的ISAR像。由于双基地时变角的影响，图7(a)和图7(b)中的二维ISAR像是“歪斜”的，图像产生了畸变，并在方位向上存在散焦现象。

依然基于最大互相关法完成包络对齐；利用PGA算法完成初相校正，完成平动运动补偿。采用基于图像对比度最大的搜索方法搜索等效旋转中心。等效旋转中心估计曲线如图8所示，图像对比度最大时对应第500个距离采样单元。以等效旋转中心位置为中心点，进行初次相位补偿，并进行虚拟慢时间采样，构造补偿系数矩阵，完成非均匀傅里叶变换，得到ISAR二维图像如图7(c)和图7(d)所示。图7(c)为定标前的ISAR像，图7(d) 为定标后的ISAR像。从图7(c)和图7(d) 可以看出，利用所提算法可以正确生成目标的二维ISAR像，验证了所提算法的有效性。相比于图7(a)和图7(b)，图7(c)和图7(d)利用所提成像算法生成的ISAR像其聚焦度优于RD成像算法生成的ISAR像。从图7(c)和图7(d)可以看出，所提算法通过初次相位补偿，亦可以有效校正“歪斜”项，消除图像畸变。图7(d)中定标后的图像形状与散射点模型一致，可等效为原图形围绕等效选择中心旋转了一定角度得到瞬时像，有利于后期目标的正确识别。

为了定量分析图像聚集度的变化程度，分别计算图7(b)和图7(d) 定标后图像的对比度和方位向3 dB宽度均值。图7(b)和图7(d)定标后图像对比度分别为16.28和24.05，方位向3 dB宽度均值分别为0.331 m和0.229 9 m。据此可以看出，基于所提成像算法获得的ISAR成像，图像的对比度有明显提升。

图9为采用与图7(c)和图7(d)采用相同的等效旋转中心估计和初次相位补偿操作后，然后基于伪WVD(Pseudo-Wigner-Ville Distribution, PWVD)时频分析算法得到t=2.5 s时ISAR图像。图9(a)是未定标的ISAR图像，图9(b)表示定标后的ISAR图像。虽然基于PWVD得到图像分辨率更高，但对于存在两个散射点的距离单元，得到的二维像中出现了交叉项，会影响目标识别。若距离单元中存在更多散射点，则会出现更为严重的交叉项干扰，影响目标识别。在此方面，相比基于PWVD的算法，所提算法具有优势。

图7 采用RD算法和所提成像算法的ISAR成像结果Fig.7 ISAR imaging results using RD and proposed algorithms

图8 等效旋转中心估计曲线Fig.8 Curve of equivalent rotation center estimation

图9 RID算法成像结果(t=2.5 s)Fig.9 Imaging results using RID algorithm (t=2.5 s)

4.2 鲁棒性分析

假定目标距离信息含有[-5 m, 5 m]均匀分布的随机误差，与文献[21]进行了仿真对比验证。文献[21]中的角度误差累积分布如图10所示。双基地角误差近似在[-0.018°, 0.018°]内均匀分布，累积转角误差近似在[-0.003 2°, 0.003 2°]内均匀分布，双基地角误差近在[-20°, 110°]内不规则分布。

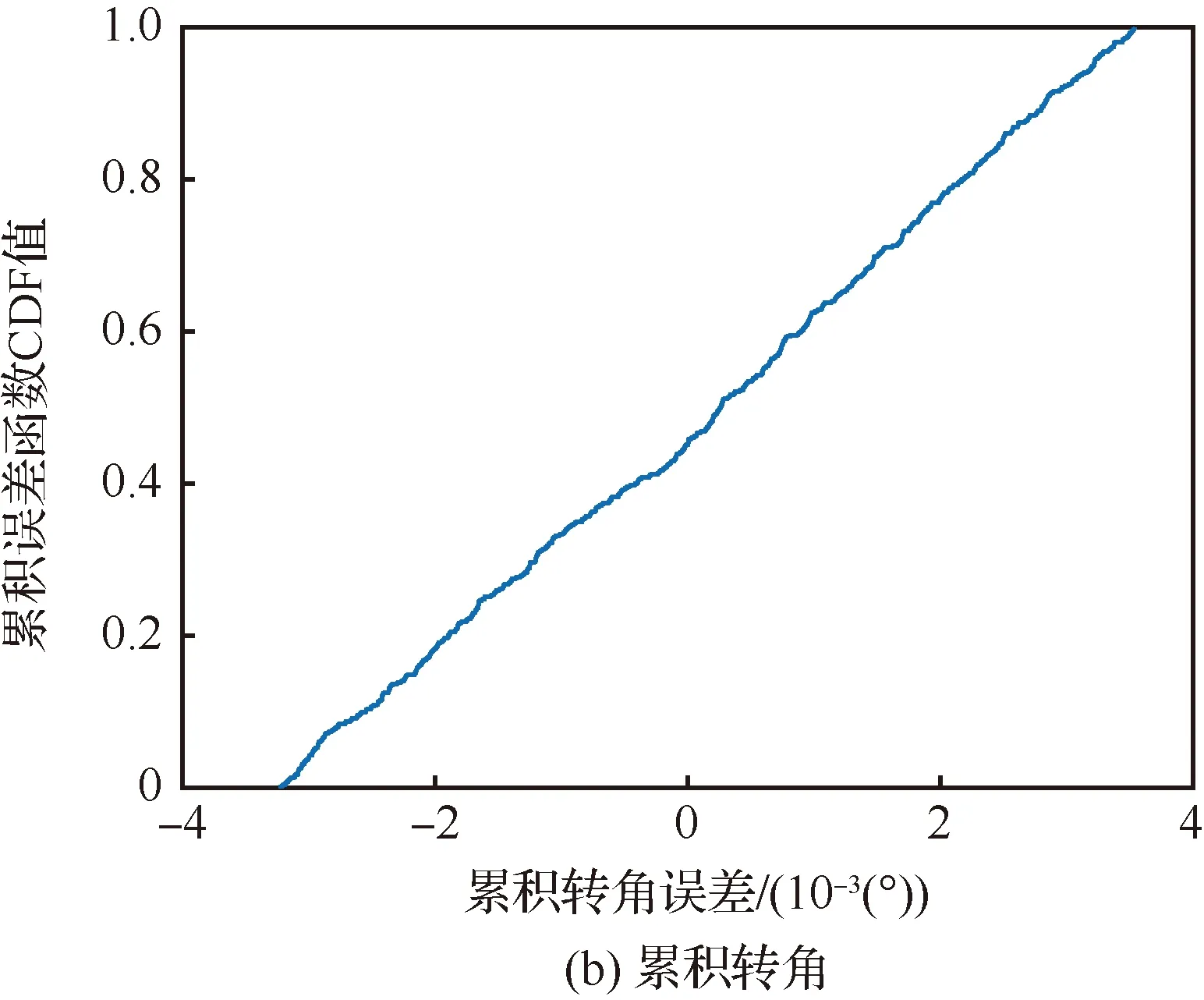
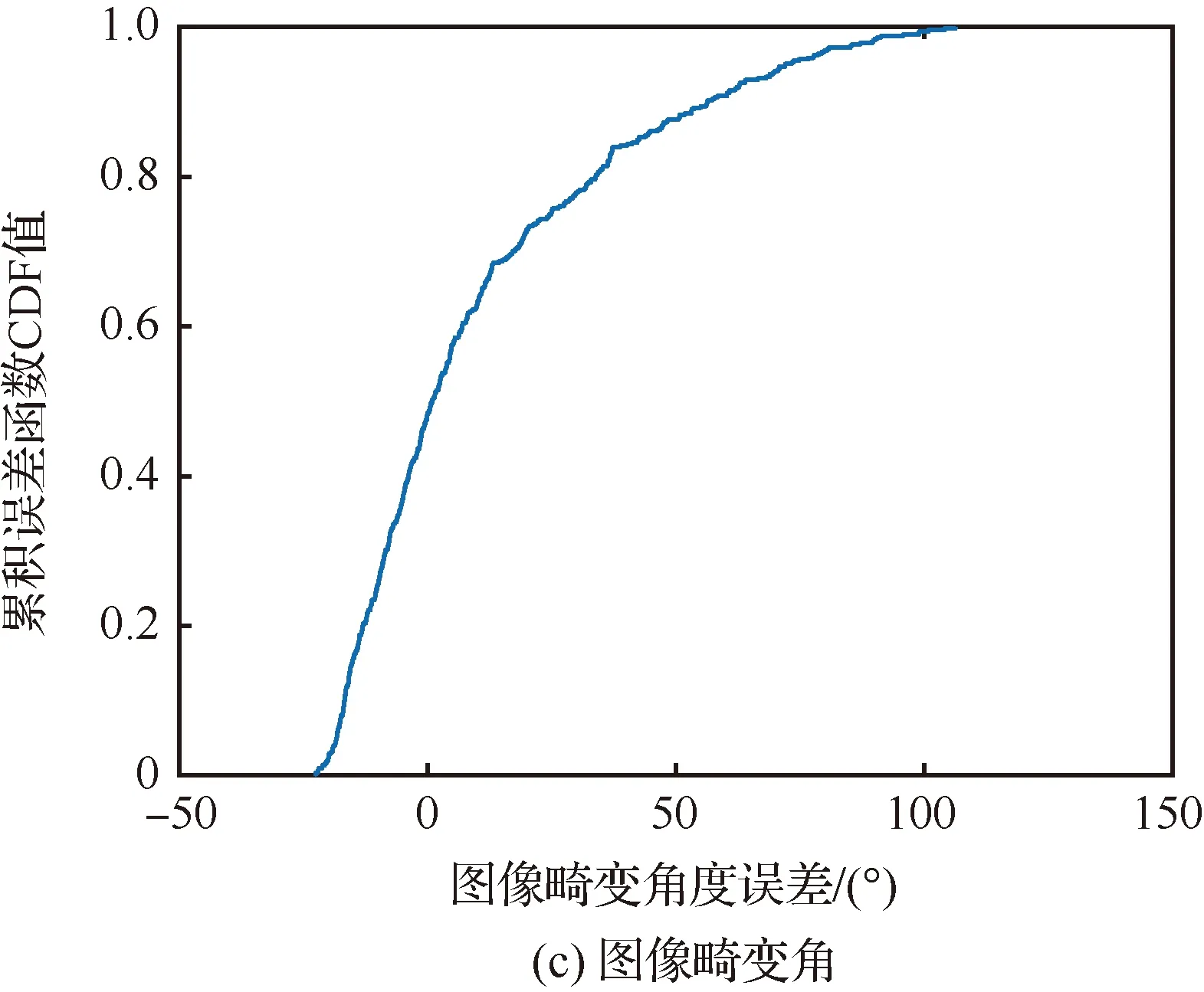
图10 各类角的误差累积分布Fig.10 Cumulative distribution of errors at different angles

在此误差条件下，所提算法能有效成像，获得目标的正确形状，消除方位向散焦(见图11(c))。采样文献[21]中的算法，部分距离单元方位向无法完成有效压缩(见图11(a))，且进行歪斜校正后无法获得目标真实形状(见图11(b))。这是由于在实际系统中，完全精确已知目标空间位置的假定是不成立的。包含误差的先验信息，会导致每个周期双基地角和累积转角均产生误差(见图10(a)和10(b))，且较小的测距误差会导致很大图像畸变角误差，(见图10(c))。这些误差影响了后续越分辨单元徙动校正和图像畸变校正。本文通过LSE算法，估计虚拟慢时间系数。在每一个双基地角均存在随机误差的情况下(见图10(a)和10(b))，基于均方误差最小的约束，亦可以精确的估计出相应系数，可以有效成像(见图11(c))，所提算法更为鲁棒。

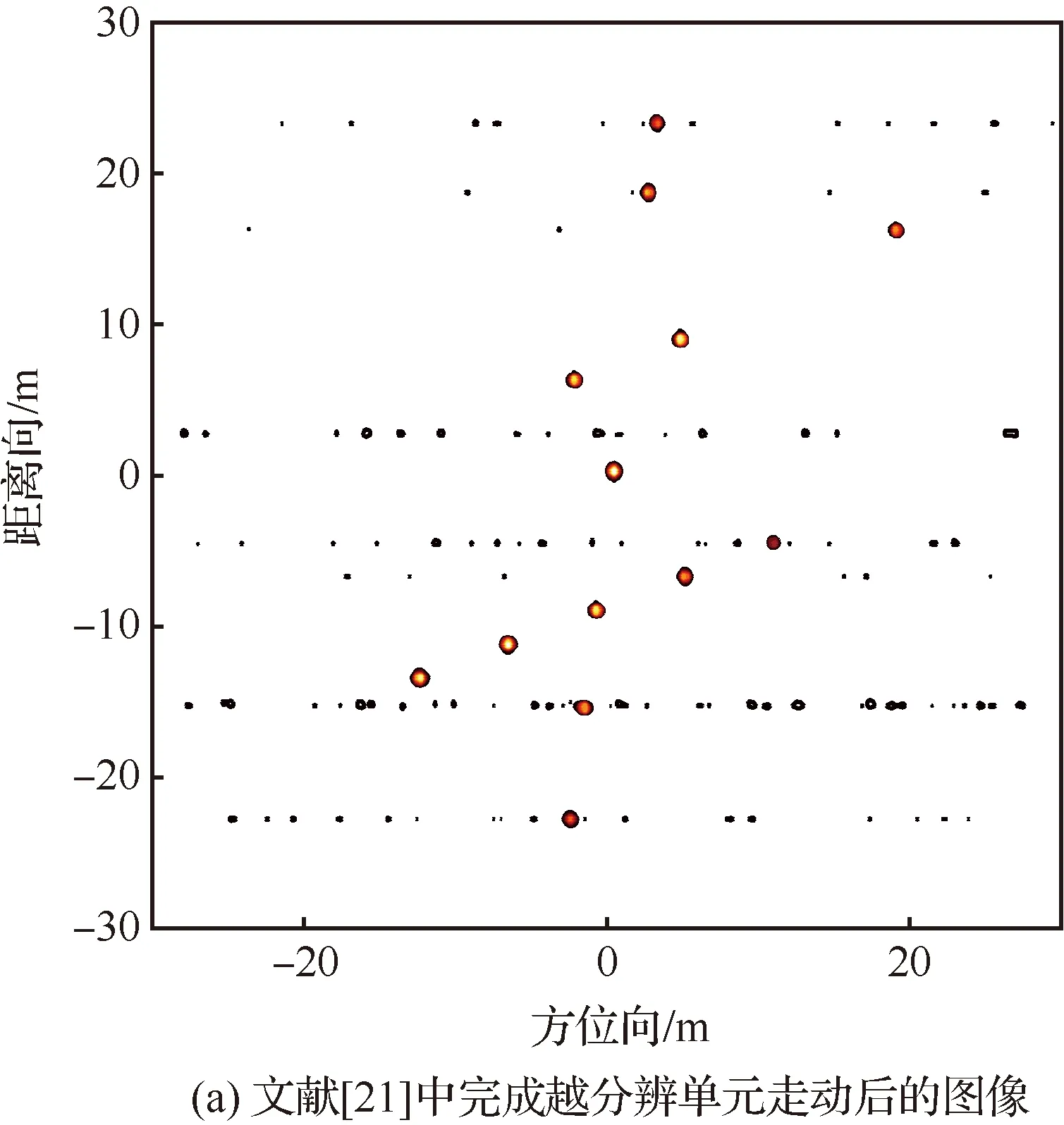
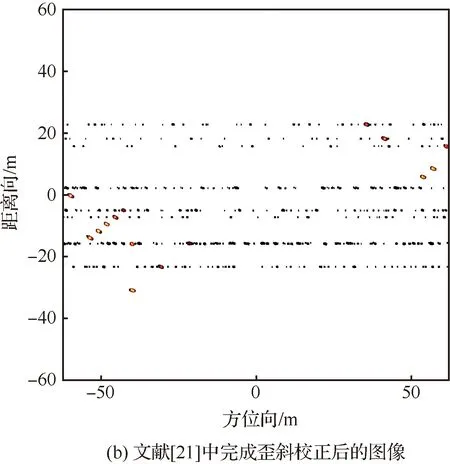
图11 误差条件下的成像结果Fig.11 Imaging results under error conditions

为了分析双基地角误差对成像算法性能的影响，将式(22)重写为

(25)

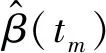
在4.1节选用的成像段中，K0和K1的值分别为0.765 6和-0.007 5，其绝对值相对较小。但对于ISAR成像，需要考察目标空间位置的变化与波长的比拟程度，误差相位的数量级要求一般与λ/8相比拟。可以通过分析其相对变化值，来定量分析参数的误差及对成像的影响。因此，进一步定义参数的相对误差：

(26)

假定测量误差εβ(tm)服从[-Δε/2,Δε/2]的均匀分布，Δε/2代表εβ(tm)误差的最大值。为了验证Δε对参数估计的影响，将Δε从0°～4°，依照步长0.2°步进，进行500次Monte Carlo仿真。图12中，Δε的值较大时，εK0和εK1的均值和方差依然很小。在Δε=4°时，εK0的均值和方差分别为0.052 9%和0.039 1%，εK1的均值和方差分别为0.304 8%和0.226 3%。在存在一定量的双基地角测量误差时，通过LSE估计，能获得高精度的K0和K1的估计值。

在Δε=4°时，计算图像对比度，仿真500次，表3给出用RD算法和所提算法得到的图像对比度的平均值。表3还给出了散射点的距离向3 dB主瓣宽度和方位向3 dB主瓣宽度平均值。

观察表3可以看出，所提算法得到的图像对比度高于RD成像算法生成的图像对比度，距离向3 dB主瓣宽度在两种成像算法下并无明显变化，方位向3 dB主瓣宽度的聚焦改善明显。这与本文所提算法可提高方位向聚焦度的理论分析一

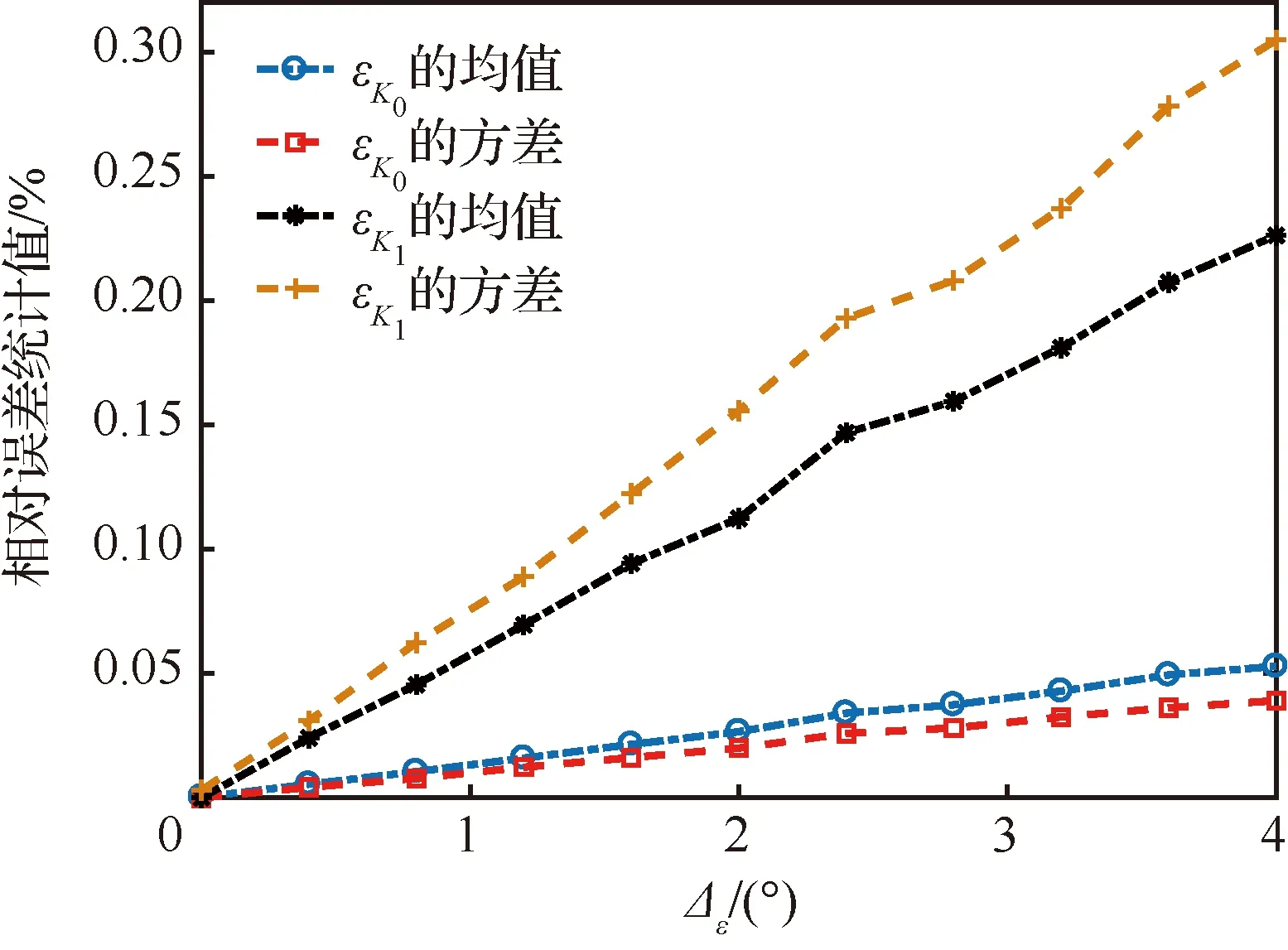
图12 Δε对K0和K1估计精度的影响Fig.12 Effects of Δε on estimation accuracy of K0 and K1

致，证明了所提算法的有效性和鲁棒性。需要说明的是，距离压缩和方位压缩时使用了Hamming窗。由于存在误差，表3中距离向和方位向3 dB宽度较理论宽度值有所增大(加Hamming窗后，3 dB距离向和方位向宽度的理论值为相应分辨率乘以系数1.3，距离向和方位向分辨率理论值分别为0.200 1×1.3=0.261 m，0.176 8×1.3=0.229 8 m)[26]。