基于FPGA数字PLL谐振频率的跟踪研究
2019-05-23余成波
余成波,张 林,龙 曦
(重庆理工大学 输变电技术研究所, 重庆 400050)
磁耦合无线电能传输技术(MCR-WPT)经过不断发展,取得了一定的进步,但其在工业领域和实际生活中的应用并不常见,许多问题还亟待解决[1-2]。在电能传输过程中,受外界障碍物(如导磁性物体)、接受端负载以及电路工作温度等各方面的影响,收发励磁线圈的电感量发生变化,从而导致谐振频率的变化,即失谐机理[3]。传输效率的急剧下降造成了电能浪费。
目前,针对失谐问题的解决方法主要集中在自适应阻抗匹配和频率跟踪两方面[4-5]。自适应阻抗匹配通过动态调节阻抗值,保证系统的谐振状态,但参数的改变会同时导致系统其他参数的变化,在实际工程应用中可操作性不强[6]。频率跟踪采用频率补偿方式动态调节系统的开关频率,但传统的频率跟踪方法存在高频切换开关损耗大、过零检测信号畸变、相位延迟等问题[7-8]。
针对上述缺陷,本文设计了一种基于FPGA实现的数字锁相环(PLL)频率跟踪MCR-WPT装置,采用双E类逆变在软开关状态下提供高频逆变电源,降低了开关管损耗。FPGA对采样信号的快速处理和对数字环路滤波器K值的灵活选择,使PLL电路的捕捉时间短,同步误差小,抗干扰能力强。根据数字PLL的电路要求,采用Verilog HDL语言自顶向下的设计思路分别设计了顶层文件、鉴相器、环路滤波器、数控振荡器以及可控分频器。最后,通过Quartus II 13.1对电路进行仿真及验证。
1 MCR-WPT锁相环电路原理分析
数字锁相环作为闭环控制系统,是负反馈控制系统,由基本的鉴相器(PD)、环路滤波器(LF)、数控振荡器(NCO)组成,如图1所示。
图1中:θ1(t)、θ2(t)分别为输入、输出信号的瞬时相位;Ud(t)为θ1(t)-θ2(t)的差值电压信号函数,Uc(t)为Ud(t)经过环路滤波器后的电压信号。应用在MCR-WPT的工作原理为:利用互感器采集发射谐振线圈的电流信号,将放大整形后得到的电压信号U1(t)作为锁相环的输入。压控振荡器的输出信号U2(t)一方面驱动双E类逆变电路工作;一方面作为反馈信号与U1(t)进行瞬时相位比较,得到二者的相位差信号Ud(t)。经过低通滤波得到平滑的控制信号Uc(t),Uc(t)控制压控振荡器输出信号U2(t),最后使U1(t)、U2(t)两个信号同频同相,从而维持发射回路的谐振状态。MCR-WPT锁相环频率跟踪电路结构如图2所示。

图1 锁相环路的闭环控制系统
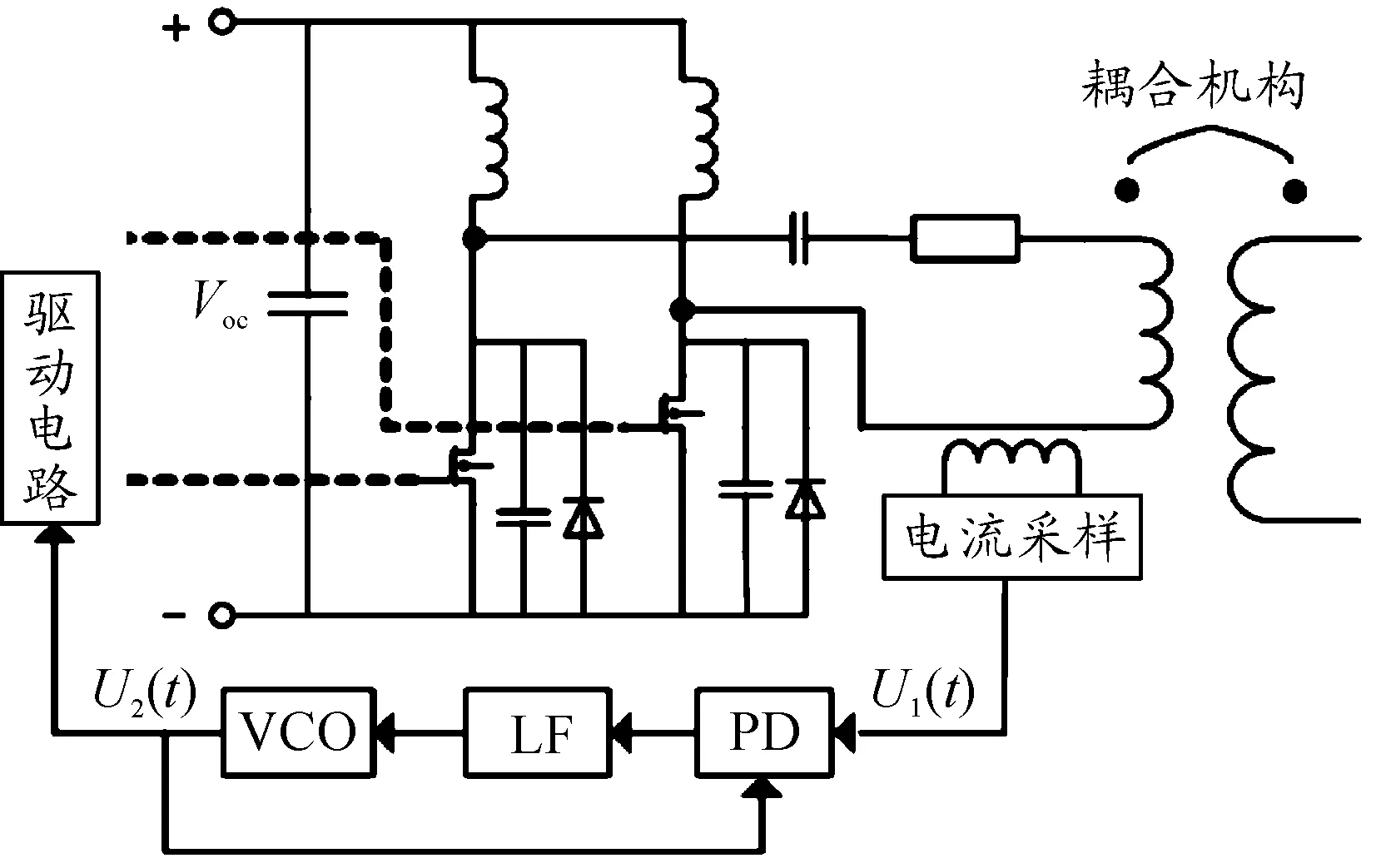
图2 MCR-WPT锁相环频率跟踪电路结构
2 二阶数字锁相环设计
2.1 鉴相器的数字化模型
鉴相器作为相位比较装置,用来检测输入信号相位θ1(t)和反馈信号θ2(t)之间的相位差θ(t),输出信号Ud(t)为相差θ(t)的函数。当输出信号电压值变化时,其相差也发生相应的变化。这种变化在具有线性特性的情况下,设计较为简单,常用的鉴相器特性曲线有正弦形特性、三角形特性、锯齿形特性等。由于采集的电流信号为正弦函数,因此采用正弦形特性的鉴相器。工程上常用乘法器与低通滤波器的串接作为模型[9],如图3(a)所示。设乘法器的系数为Km,输入信号Ui(t)为
Ui(t)=Uisin[ω0+θ1(t)]
(1)
式中:ω0为压控振荡器的固有频率;θ1(t)为输入信号的瞬时相位。反馈输出信号U0(t)为
Uo(t)=Uosin[ω0+θ2(t)]
(2)
式中:θ2(t) 为输出信号的瞬时相位。输入信号和输出信号相乘后,经过低通滤波器滤除2ω的高频成分,得到输出电压Ud(t)。
Ud(t)=0.5KmUiUocos[θ1(t)-θ2(t)]
(3)
正弦鉴相器的特性曲线如图3(b)所示。将其近似为线性曲线,则在(-π/2,π/2)内近似为斜率为Ud的直线,在(π/2,3π/2)内近似为斜率为-Ud的直线。因此,当相位误差满足-π/2 <θ(t)<π/2时,式(2)可近似为
Ud(t)≈Vdθ(t)=Kdθ(t)
(4)
式中:Kd= 0.5KmUiUo,为鉴相器的鉴相增益。串接的低通滤波器采用FIR实现,过渡带设计为200~600 Hz,采样频率为8 kHz(大于输入信号频率的两倍即可),通带纹波为0.03 dB、阻带纹波为0.05 dB,采用firpm和fir1函数分别设计最优滤波器和窗函数滤波器。3种FIR滤波器的设计如图4所示。
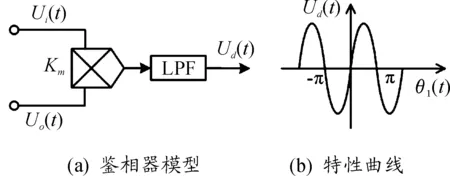
图3 正弦鉴相器
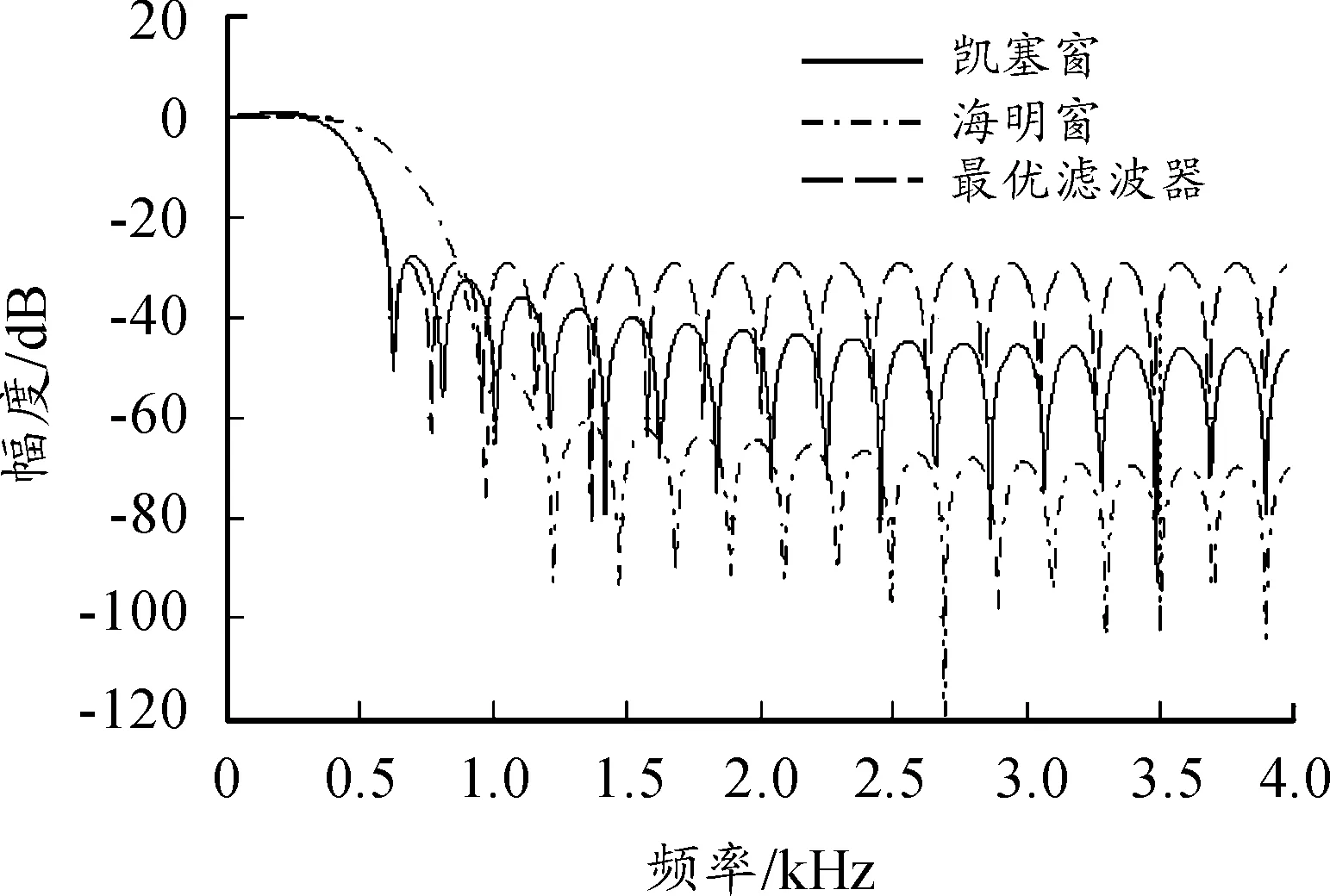
图4 3种FIR滤波器的设计
不考虑低通滤波器的作用,对鉴相器做近似线性化处理,相当于增益为Kd的线性增益模块:
Kd=0.5KmUiUo
(5)
2.2 环路滤波器的数字化模型
对于任何频率的信号,鉴相器的响应都是乘以1个增益常数Kd,其相位响应为0,而压控振荡器在整个电路中产生固定的90°相移。因此,整个锁相环的稳定性取决于环路滤波器的特性。环路滤波器在PLL电路中不仅可以滤除误差电压Ud(t)中的高频成分和噪声,还控制着环路相位校正的速度与精度,保证环路所要求的性能,增加系统的稳定性。
传统的RC滤波器具有相位滞后的特点,不利于提高环路的相位裕度,且无法在输入信号和本地振荡频率有频差的情况下达到稳态相差为0。相比之下,采用有源比例积分滤波器作为环路滤波电路则具有良好的稳定性,在存在频差的情况下,稳态相差可达0,有源比例积分电路如图5所示。

图5 有源比例积分电路
利用虚断、虚短计算出滤波电路的传输函数:
F(s)= -A· (1 +sτ2)/1 +sτ1
(6)
式中:τ1=(R1+AR1+R2)C;τ2=R2C;A为运算放大器无反馈时的电压增益。若运算放大器增益A足够大,则式(6)可以近似为
F(s)=-(1+sτ2)/sR1C
(7)
由式(7)可知:分子中只有1个时间积分因子,因此会引起90°的相位滞后,但分母的积分因子会引起相位超前。随着频率的增加,相位超前越多,越接近90°。令τ1=R1C,利用Matlab绘制不同时间积分下有源比例积分器的伯德图,如图6所示。由图6可知:在零频附近相位滞后为90°,相位的滞后量随着频率的增加逐渐减小。将式(7)模拟系统转换为数字系统,数字化函数为
(8)
式中:T为采样周期;τ1、τ2为时间积分常数,C1=(2τ2+T)/2τ1,C1=T/τ1。对式(8)进行数字化结构设计,环路滤波器Z域结构如图7所示。
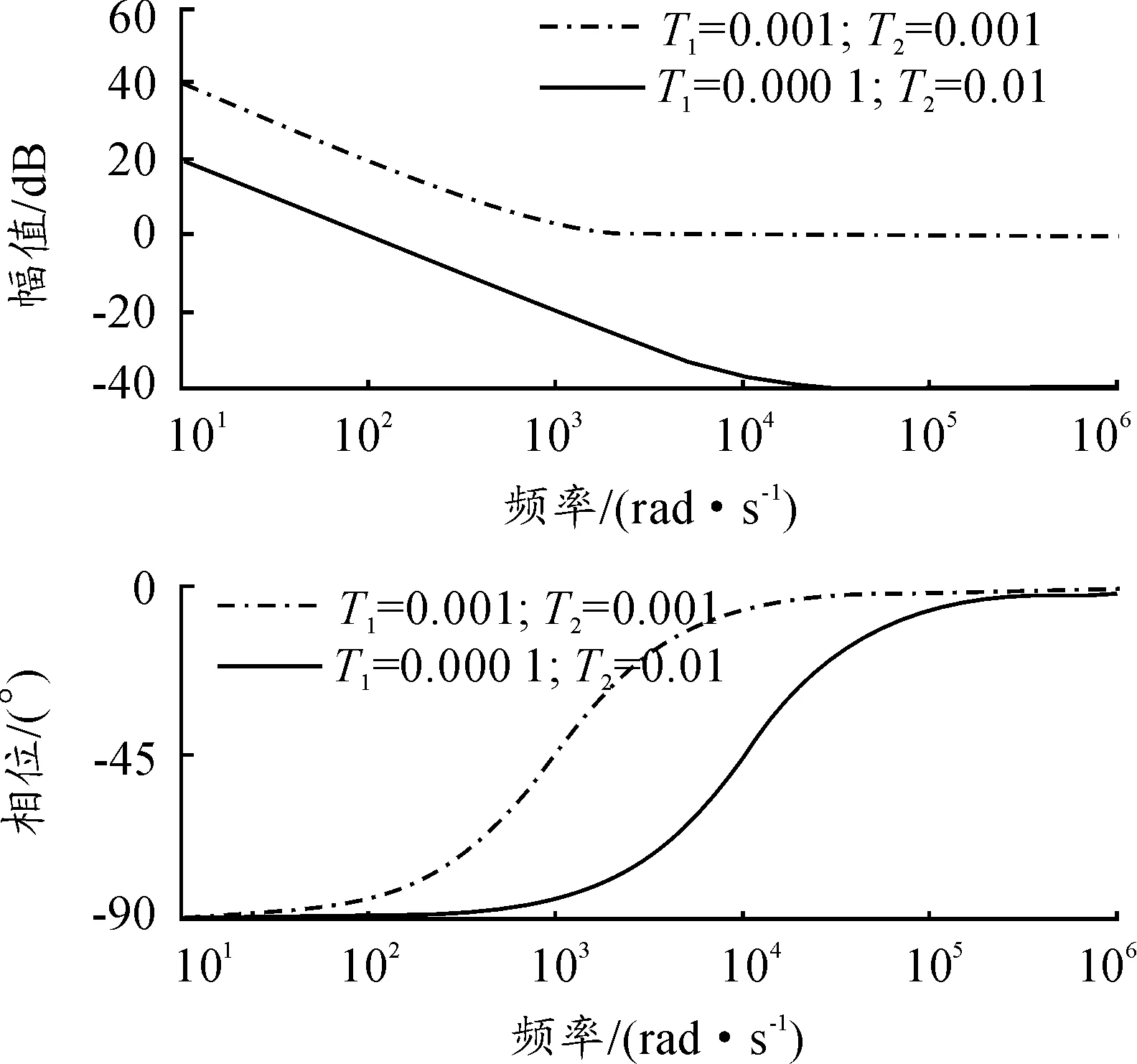
图6 有源比例积分伯德图
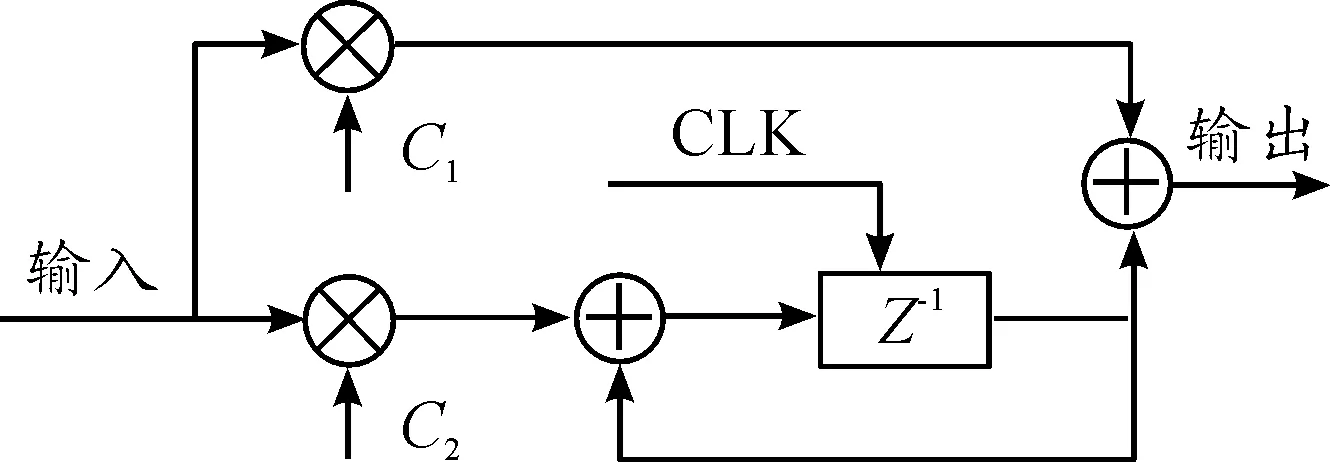
图7 环路滤波器Z域结构
根据采用周期T、时间积分常数τ1、τ2可以得到C1、C2的数值。根据图7数字化结构,采用Verilog HDL语言设计数字电路,可得到2阶环路滤波器RTL原理图,如图8所示。
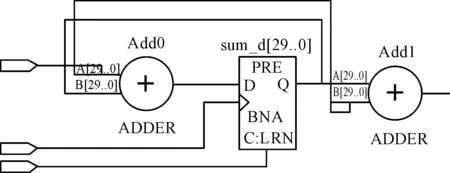
图8 2阶环路滤波器RTL原理图
2.3 数控振荡器的数字化模型
振荡器是一个电压与频率的转换装置。压控振荡器(VCO)与数控振荡器(NCO)的作用基本相同,压控振荡器通过电压控制振荡器的角频率输出,其输出信号角频率与输入信号电压值之间的关系为
ωc(t)=ω0+Κ0Uc(t)
(9)
式中:ω0为压控振荡器的固有频率;K0为控制灵敏度,其控制特性如图9所示。由鉴相器特性可知:当VCO输入电压为0时,振荡角频率为ω0;在线性控制区域内,控制灵敏度K0越大,则线性曲线斜率越大。由鉴相器输入特性可知:振荡器的输出信号为瞬时相位形式,对式(9)两边同时积分,得到输出信号的瞬时相位
(10)
由式(10)可知:瞬时相位值θ2(t)将ω0t作为基准值,1/P作为积分因子,VCO的输出信号和式(2)一致。
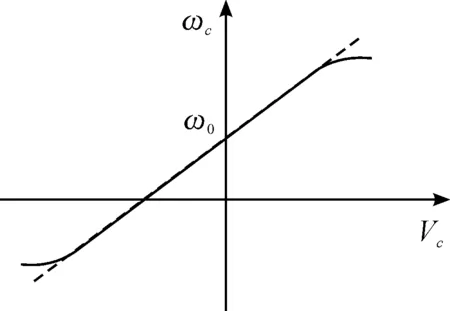
图9 压控振荡器的控制特性
数字域中,数控振荡器通过产生正交的正余弦样本构成幅度-相位的转换电路。在系统时钟的控制下,由相位累加器对输入频率字不断累加,得到以该频率字为步长的数字相位,再通过相位模块进行初始相位偏移,得到输出的相位。NCO输出信号频率与输入电压值之间的关系为
ω(n)=2πf0+2π0Uc(n)fclk/2Bnco
(11)
式中:fclk为时钟驱动频率;Bnco为相位字宽,是NCO的频率控制的自然数,控制灵敏度K0=fclk/ 2BncoHz/V。对式(11)进行Z变换,得到NCO的数字模型:
(12)
式中K0′=K0Tclk。至此,获得了数字锁相环的鉴相器、环路滤波器和数控振荡器的数字化模型。
3 二阶数字锁相环的仿真与实验
各个环节的设计完成之后,将输入信号、输出信号以及各环节组成部分进行相应的变换,得到锁相环Z域模型,如图10所示。

图10 锁相环的Z域相位模型
由图10可知:输入相位θ1(z)和输出响应相位θ2(z)的闭环传递函数为
(13)
将式(2)、(8)和(12)代入式(13)可得数字2阶锁相环的系统函数
(14)
式中:Kz=KdK0′,Kz称为数字锁相环的增益,其大小直接影响环路的稳态差异、捕获宽带等重要性能。至此,总结数字锁相环的设计步骤如下:
步骤1根据设计要求,确定相位增益Kz、系统采样频率fs、环路阻尼系数ζ和固有振荡频率ωn。
步骤2计算C1、C2。
在Quartus中设置IP核参数(鉴相器、数控振荡器)和环路滤波器的Verilog HDL设计参数,PLL数字电路参数设计如表1示。
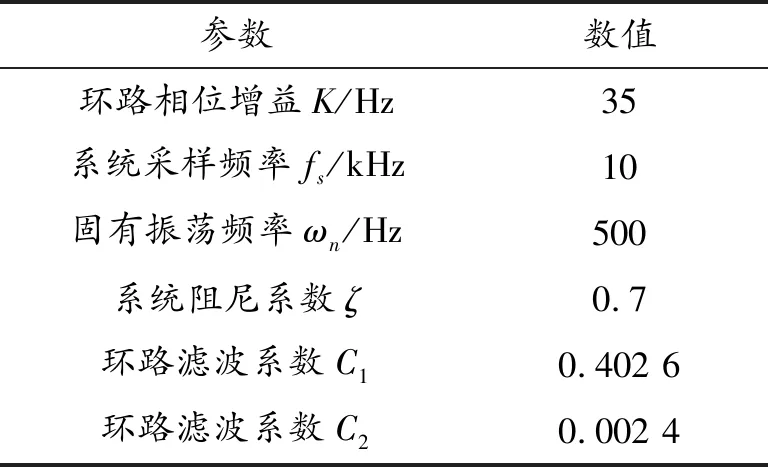
表1 PLL数字电路参数设计
经过综合编译Verilog HDL代码后,启动ModelSim仿真工作。在wave窗口从上到下依次添加输出信号波形、输入信号波形以及鉴相器两路波形信号,仿真波形如图11所示。
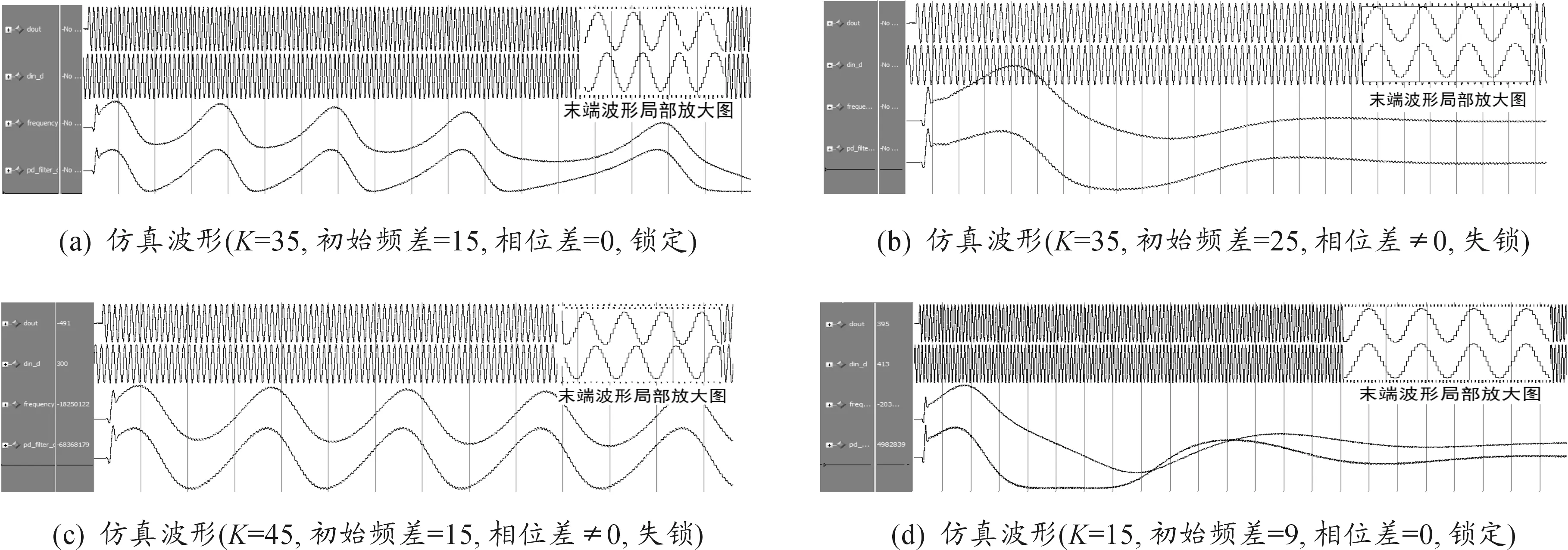
图11 二阶锁相环ModeSim仿真波形
观察电路仿真至稳态时波形末端的局部放大图可以判断是否完成相位的锁相。其中,图11(a)、(d)完成相位锁定,图11(b)、(c)相位失锁。对比图11(a)、(b)可知:增益K一定时,初始频差越小,锁相速度越快;图11(a)、(c)中,初始频差一定时,增益越大,锁相速度越快。由图11(d)可知:环路能正常锁定,发射线圈中的电流和电压信号同相位。综合对比分析可知:
1) 环路能否成功锁定跟踪,与环路增益大小、电流和电压信号初始频差有关。
2) 环路参数确定后,环路最大增益确定。当环路增益大于该值,环路失锁。初始频差相同的情况下,环路增益越小,捕获时间越长。
3) 无论环路是否存在初始频差,当环路锁定后,其稳态相差基本为0。
FPGA管脚分配后,将数字电路下载至开发版,搭建线电能传输装置,如图12所示。测试在有无数字PLL控制下MCR-WPT电路的传输效率和传输功率,实验结果如图13、14所示。

图12 频率跟踪磁耦合无线电能传输装置
在传输距离为10 cm时,数字PLL控制的电路传输效率提高了30%,功率提高了50 W。采用数字PLL跟踪控制电路谐振频率保证了发射电路和接受电路处于具有较高的耦合系数和强耦合的工作状态,因此传输效率得到了提高。同时,电路的谐振状态也保证了电路处于纯电阻状态,电路总阻抗减少,因此负载输出功率得到了提高,电路整体性能增强。
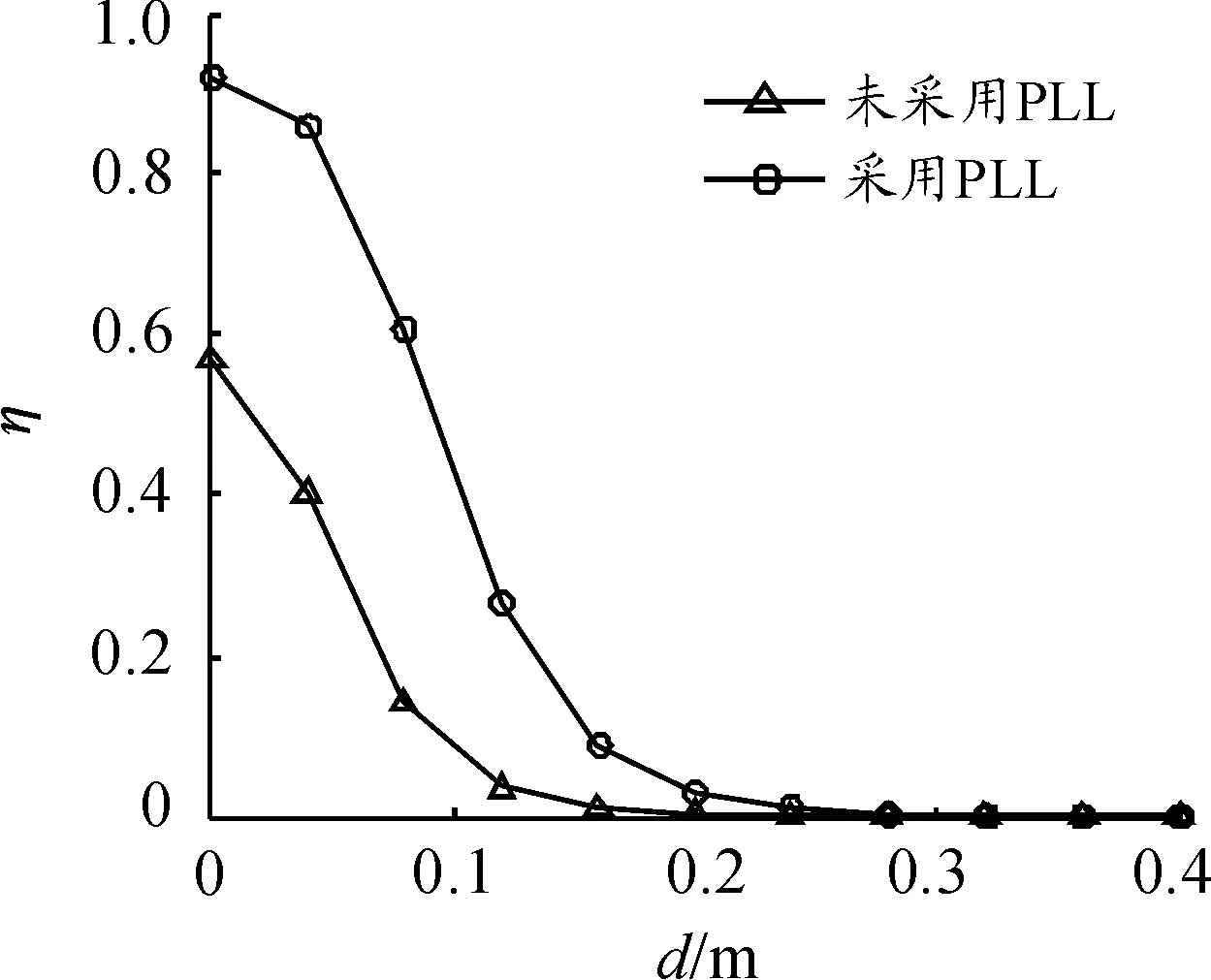
图13 不同传输距离下的传输效率
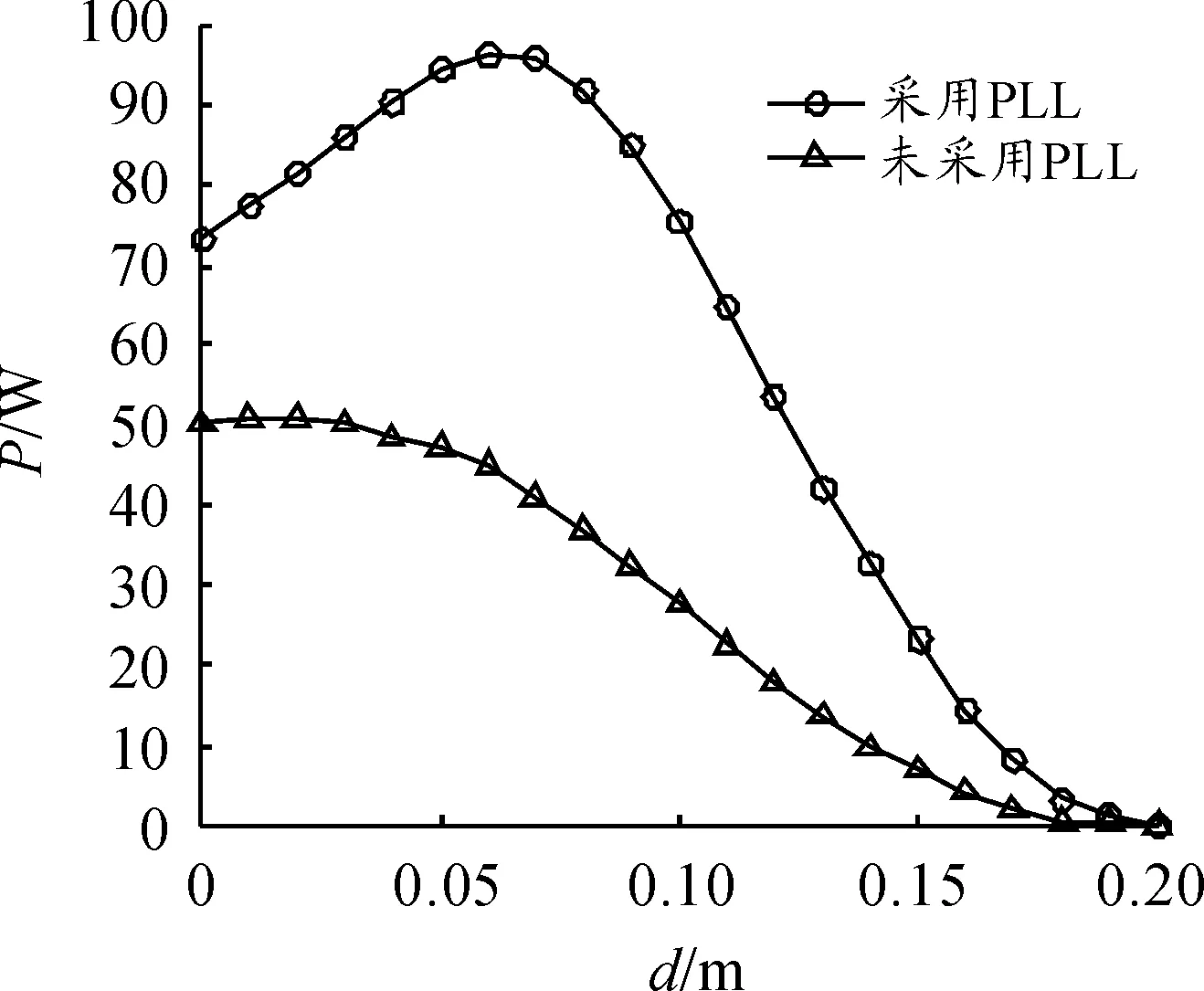
图14 不同传输距离下的传输功率
4 结术语
通过数字PLL电路仿真和实验结果可知:数字PLL环路能实现无线电能传输电路中谐振频率的跟踪控制,从而提高系统的传输效率和功率。环路的增益、带宽决定了环路能否实现频率跟踪。数字PLL电路能有效地解决谐振频率漂移问题,为无线电能传输系统效率的提高提供了一定的参考。
