电动助力转向系统的智能控制研究

彭 滔，周 鹏，胡桃川

(重庆理工大学 两江人工智能学院， 重庆 401135)

随着对汽车行驶安全要求的不断提高，人们对汽车的平顺性和操纵稳定性也提出了越来越高的要求。通过合理设计车轮定位参数可以使得汽车具有一定的回正能力，从而提高汽车的操纵稳定性，但却增加了汽车转向阻力。特别是在低速行驶时，容易造成驾驶员疲劳，不利于驾驶时舒适性的提高。汽车助力转向系统通过借助外力来提高转向能力，对提高汽车操纵稳定性有十分积极的意义[1-2]。

汽车电动助力转向(electric power steering,EPS)具有减轻自重、可移植性好、结构简单、布置灵活等特点，紧扣未来汽车“绿色”、“智能”的发展主题，已成为当今汽车助力系统广泛采用的主流技术，也是世界汽车技术发展的研究热点之一[3-4]。

EPS是一套复杂的机电一体化系统，主要包括控制器、转向盘转矩传感器、车速传感器、电流传感器、助力电机以及减速机构、机械式转向器、电源等部分[5]。EPS控制的关键问题是根据汽车的运行状态确定助力电机输出力矩，并设计电机控制器实现助力电机力矩的跟踪。

许多研究者从不同方面运用不同的方法进行了研究。任夏楠等[6]利用助力误差，在高低两种行驶工况下阐述了对阻力特性曲线的设计原理，并探讨了EPS助力特性曲线的相关几何特征。张永辉等[7]以驾驶员理想转向盘力矩为依据，设计了电动汽车的助力特性曲线，对电动汽车EPS助力曲线进行了设计与评价。李志鹏等[4]针对采用PID控制的电动助力转向系统中出现的积分饱和现象，提出了基于模糊和anti-windup变结构自适应PID的抗饱和特性控制器。李靖等[8]针对汽车EPS系统的非线性实时变化问题，通过模糊算法，设计了EPS的助力特性曲线，建立了助力电机电流和转向杆位移的预测控制模型，实现对EPS的预测控制。孔令强等[9]通过建立包括机械模型、电动机模型、2自由度转向模型和轮胎模型的EPS模型，设计了H∞输出反馈控制器。赵万忠等[10]利用EPS及整车的2自由度模型，通过构建系统状态空间方程和增广被控对象矩阵，运用H∞方法极小化系统中各种干扰对被控输出的影响，并在此基础上应用H2方法对系统进行优化。闫启迪等[11]针对电动叉车电动助力转向系统，基于2自由度模型设计了鲁棒H∞控制器，并运用遗传算法对控制器的加权函数参数进行优化。邹左明[12]将系统的外界干扰、系统建模误差等因素看作是一个广义的外干扰系统，对系统可观测干扰进行观测，提出一种基于干扰观测器的动态面滑模控制。王金波等[13]考虑驾驶员熟练程度，提出了一种跟踪期望驾驶特性的汽车电动助力转向系统控制策略，改善了汽车的操纵稳定性。陈国平等[14]在动力学模型的基础上，考虑了系统存在的不确定因素，融合模糊逻辑和滑模变结构控制，研究了电动轮汽车差动转向稳定性控制策略。

目前EPS系统常用的控制策略主要是PID，对系统中存在的模型不确定性和路面干扰等信息难以很好地控制。针对该问题，本文根据转向盘转矩信号和车速信号确定助力电机的目标转矩，利用径向基函数(radial basis function,RBF) 神经网络对助力电机的电流参数设计智能控制器，通过助力电机快速跟踪目标电流来实现助力电机施加在转向轴上的助力转矩快速跟随目标转矩，从而达到EPS转向助力的目标。RBF神经网络具有较好的自适应性和泛化性等优点，能弥补控制系统中的非线性、不确定性和未知信息等不利因素，提高了转向控制系统的控制精度、鲁棒性和自适应能力。

1 EPS动力学模型

EPS系统主要由控制器、传感器、助力电机和机械结构等部件构成。对其进行动力学建模后得到方向盘、输入转向柱、助力电机、输出转向柱、齿轮齿条和左右轮等6个动力学元器件之间的动力学关系，系统结构如图1所示[4]。

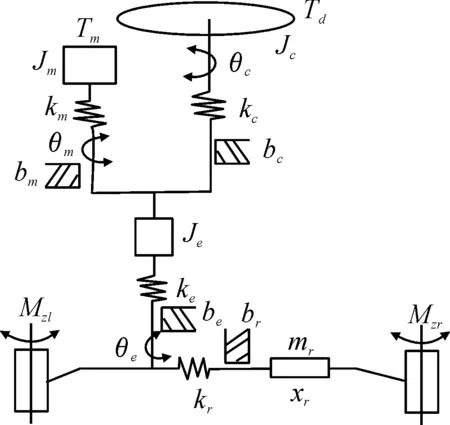
图1 EPS系统结构

方向盘转角和下转向轴之间的动力学关系[4]为

(1)

其中：θc为方向盘的输入转角；θe为下转向柱的转角；Jc为方向盘转动惯量；bc为方向盘阻尼系数；Td为方向盘输入力矩；Kc为输入转向柱扭转刚度。

助力电机与下转向轴之间的动力学关系为

(2)

其中：θm为助力电机的转角；Jm为助力电机转动惯量；bm为助力电机阻尼系数；Tm为电机转矩；Km为助力电机转矩扭转刚度；G为电机减速机构传动比。

下转向轴与齿轮齿条转向器之间的动力学关系为

GKc(θm-Gθe)

(3)

其中：Je为下转向柱转动惯量；be为下转向柱的阻尼系数；Kc为上转向柱扭转刚度；Ke为下转向柱扭转刚度；θe为下转向柱的转角。

齿转齿条转向器与其端作用力的动力学关系为

(4)

其中：xr为齿轮位移；mr为齿轮质量；br为齿轮阻尼系数；Kr为齿轮刚度；Fσ为齿轮端作用力；rp为小齿轮的分度圆半径。

转向器端作用力与车轮转向角之间的动力学关系为

(5)

其中：JFω为车轮绕主销的转动惯量；bFω为绕主销阻尼系数；KFωz为绕主销转动刚度；A为转向器端到前轮的力臂传动比；Mz为前轮的回正力矩；θFω为前轮转角。

车轮回正力矩的动力学关系为

(6)

其中：Mzl为左前轮的回正力矩；Mzr为右前轮的回正力矩；γ为主销后倾角；β为主销内倾角。

2 智能控制器设计

2.1 控制策略

EPS控制方案包括上层的助力电机目标电流确定策略和下层的电流闭环控制策略两个部分[15]。

助力电机目标电流的具体确定方法主要有实时计算法和利用助力特性曲线计算两种方法。常用的方法根据转向盘转矩信号Td和车速信号V，利用助力特性曲线确定目标电流Im。助力电机利用反馈实测电流I与目标电流Im构成闭环，得到电流闭环控制结构示意图，如2所示。

图2 控制系统结构示意图

常用的助力特性曲线有直线型、折线性和曲线型3类。本文中选用如图3所示的直线型助力特性曲线来计算助力目标电流Im，其中Td为转向盘转矩。如图3所示，在助力区内力矩Td与电流Im成线性关系，在某一车速范围内的助力曲线函数可表达为[16]

(7)

其中：Td0为开始助力时转向盘的输入扭矩；Imax为助力电机最大工作电流；K(V)为助力增益系数。为了使驾驶员获得更好的操作性和路感，助力特性曲线应能充分协调低速轻便、高速沉稳的助力特性，因此式(7)中的K(V)值随车速的增加而减小。

图3 直线型助力特性曲线

2.2 智能控制器设计

电动助力转向系统需要满足稳定性、迅速性和准确性的要求，但电机中存在的强非线性和不确定性是控制器设计中的难点。神经网络能以任意精度逼近任意非线性函数，具有自组织、自适应、自学习、泛化性和容错性强等优点，能弥补控制系统中的非线性、不确定性和未知信息等因素的影响，提高鲁棒性和自适应能力[17]。本文利用RBF神经网络对任意非线性函数全局任意精度的逼近能力设计智能控制器，实现对系统的控制[18-21]。

2.2.1助力电机转矩模型

本文采用永磁直流电机作为助力电机，由于电机自感电动势很小，可以忽略不计。因此，电机端电压Um与电枢的电阻R和电流Im、反电动势常数Kb、转速Nm之间的关系可以表示为[19]

Um=R·Im+Kb·Nm

(8)

由于转矩与电枢电流成正比，可令Ka为转矩常数，则式(8)可改写为

Um=Ka·Tm+Kb·Nm

(9)

2.2.2神经网络控制器设计

根据式(8)和(9)可知，电机转矩有电压和电流两种控制方式，其中电压控制是开环控制方式，而电流控制是通过电流传感器测得电枢电流信号构成反馈通道形成的闭环控制方式。开环控制结构简单，但控制精度不高，闭环控制则控制精度高，抗干扰能力强。

本文采用控制电流的闭环控制方式，利用RBF神经网络对电流参数设计智能控制器，控制器中的神经网络输入为电流偏差信号(即状态误差)，输出为电流的控制量，实现对电机转矩控制。RBF神经网络属于一类线性化参数的神经网络，可以表示为[20]

(10)

其中：Z=[z1,…,zq]∈ΩZ⊂Rq是输入向量；W=[w1,…,wn]T∈Rn是权值向量；n>1是RBF神经网络节点数；S(Z)=[s1(Z),…,sn(Z)]T；si(·)是径向基函数，本文采用如下高斯函数定义：

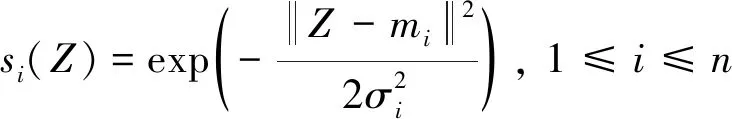
(11)

在助力转向电机控制中，只有电流误差信号Ie=I-Im这1个状态输入(即Z=Ie)，因此RBF神经网络的输入层只需要1个神经元，神经网络输出为

(12)

其中I是助力电机实际输出电流。

2.2.3神经网络学习算法

(13)

(14)

(15)

(16)

同理可得：

(17)

wi(n+1)-wi(n)=-η(I-Im)si(Z)

(18)

其中η为学习率。由式(16)～(18)可以对mi、σi、wi进行调整。

3 仿真研究

为了验证本文所提方法的正确性和有效性，在北京中通天立公司研发的TAT-6/TL型“电动助力转向在环仿真实验台”EPS实验台架(图4)中，采集了分别代表低速(V=23.11 km/h)、中速(V=73.14 km/h)和高速(V=152.4 km/h)的3组数据，利用Matlab平台进行仿真研究。

图4 TAT- 6/TL型EPS实验台架

仿真研究中，选取神经元数n=100，参数初值为m=0，w=0，σ=1，学习率η=0.8。TAT- 6/TL型EPS实验台架中的助力特性函数为：

(19)

在仿真中，根据式(10)～(12)和(16)～(18)建立高斯函数神经网络和参数更新，利用PID控制得到的数据对神经网络进行训练，得到mi、σi、ωi的值。再读取转矩信号Td和车速信号V的实验数据，根据式(19)计算出对应的目标电流值Im，利用神经网络控制器式(12)，得到助力电机实际电流值I。

将本文提出的智能控制效果与TAT- 6/TL型EPS实验台架中采用PID控制(参数分别为P=1，I=0.1，D=0)时的效果进行了对比，结果如图5～10所示。

从图5～7中可以看出：两种控制方法的控制效果均是在低速时助力电流大，高速时助力电流小，符合助力转向时保证驾驶员路感的要求。

从图8～10中的控制电流误差可以看出：本文提出的智能控制方法在3个速度的电流误差整体明显好于PID控制效果，在低速和高速阶段的控制效果尤为明显。在中速阶段，虽然PID控制在[0,100]、[180,320]和[375,400]这3个时间段内表现出了良好的控制效果，控制误差约为0，但在[100,180]和[320,375]两个时间段内，误差出现了较大波动，最大误差达到-2.02，而智能控制的电流误差几乎在整个时间段内都保持在[-0.5,0.5]的范围内。

图5 低速助力曲线(V=23.11 km/h)

图6 中速助力曲线(V=73.14 km/h)

图7 高速助力曲线(V=152.4 km/h)

图8 低速助力电流误差曲线

图9 中速助力电流误差曲线

图10 高速助力电流误差曲线

通过对比分析认为：由于RBF神经网络能弥补控制系统中的非线性、不确定性和未知信息等因素，使得本文提出的智能控制器有更好的控制精度和平稳性，提高了电动助力转向系统的鲁棒性和自适应能力。

4 结束语

本文基于EPS提出了一种智能控制方法，利用直线型助力特性曲线确定目标电流，再利用RBF神经网络对助力电机电流设计了控制器，并利用BP学习算法对神经网络权值、中心点和方差进行调节。该方案易于实现，同时保证了转向控制系统具有较高自适应性和控制精度，并通过采集实验台架不同速度下的实验数据进行仿真研究，验证了所提控制方案能实现EPS的助力控制。