基于CFD的空冷塔烟气排放数值研究

王国峰，赵巧男，张皓男，杨 硕

(沈阳工程学院 辽宁省洁净燃烧发电与供热技术重点实验室， 沈阳 110136)

在水资源相对匮乏的国家和地区自然对流空冷塔(natural draft cooling tower，NDCT)作为一种有效的节水型发电设备被广泛应用，国内外众多学者相继开展了广泛的数值研究[1-5]。Al-Waked[6-7]利用通用CFD软件Fluent对自然通风逆流湿式冷却塔进行了三维数值计算，分析了环境侧风影响。Kapas[8]通过数值模拟和试验研究指出：随着侧向风速的增加，空冷塔冷却能力逐渐减少。浮杰[9]比较了烟塔合一条件下的烟羽抬升高度，并与传统的烟囱进行了比对，得到了塔内流动与热力性能之间的关系。国内外学者在环境侧风、塔内热环境、水冷系统、结构改进以及腐蚀等众多方向进行了大量研究，取得了众多成果。通过对空冷塔流动及换热数学模型的研究，发现国内外众多学者在空冷塔的研究中更多的是设置计算域迎风面为速度入口边界条件，速度大小采用幂指数风廓线公式。这种方法的优点是能描述垂直方向上的速度分布趋势，缺点是无法描述浮力对空气流动产生的影响，而空冷塔恰恰是基于自然对流理论产生空气流动及换热。为了解决浮力问题，国内外学者利用Boussinesq假设来处理由密度差产生的浮力项影响。通过使用Boussinesq假设密度为常值，消除浮力项中的密度变化。不过这种假设存在缺陷，首先假设仅在流体密度变化很小时适用；其次Boussinesq假设不能与组分计算同时使用，这就意味着无法描述烟气扩散问题。

本文首先通过建立定常、无内热源、三维、可压缩自然对流的牛顿流体数学模型解决空冷塔内部由于温度及高度变化而引起浮力变化问题，然后利用浮力驱动自然对流模型，使用数值方法研究在不同环境温度、风速条件下对烟羽抬升高度和污染物扩散的影响。本文采用的方法与Boussinesq求解方法有所区别，Boussinesq方法是近似认为ρ=ρ0(1-βΔT)来消掉浮力项中的密度ρ，而本文则采用理想气体利用瑞利数(Ra)和普朗特数(Pr)求解热膨胀系数，进而求解动量变化。这种数学方法不仅解决了浮力驱动自然对流的问题，同时也解决了多组分烟气扩散的问题。

1 物理模型

本文研究的对象为自然空冷塔，该类型空冷塔主要依靠底部散热器对空气进行加热，然后利用塔的高度，在塔内形成自然对流。空冷塔及散热器的基本几何参数如表1所示。

表1 空冷塔几何参数

建立全尺度数值分析模型(如图1所示)，模型采用正方形的外边界，底部为地面设置，四周边界距中心1 000 m，顶部距离地面450 m，消除边界对冷却塔的影响。计算域尺寸为2 000 m(x)×2 000 m(y) ×450 m(z)(分别对应x、y、z轴)，其中(x)、(y)、(z)分别为计算模型在各风向下沿x、y、z方向的计算长度。四周边界采用通风压力进口设置，压力随高度h变化。顶部采用压力出口设置，压力与高度相关。对塔身、散热器以及周围流场采用结构化网格进行划分。由于该模型较大，计算流域较广，使得网格划分变得十分困难，为此，在网格划分过程中采用区域控制的方式实现网格由密到疏的过渡。同时，本文进行网格无关性验证，保证计算稳定性及准确性。图2为风冷塔的仿真分析模型及网格。

图1 空冷塔示意图

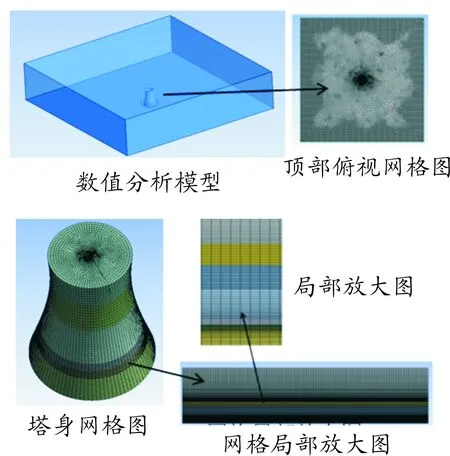
图2 风冷塔的仿真分析模型及网格

2 数学模型

目前针对空冷塔较为常见的解决浮力的方法有两种。

一种是采用幂指数风廓线公式(如式(1)所示)来描述侧向风沿高度的变化[10]。这种方法既解决了侧向风的影响，也解决了浮力问题。其优点是能描述垂直方向上速度的分布趋势，因计算采用不可压缩流体，能节省计算资源，提升计算速度。但是利用速度进口的缺点是无法描述浮力在垂直方向上对空气流动产生的影响，特别是对塔身及塔内的影响，因此在现有文献中该分析方法更加关注塔外空气的流动问题。

w=wref(z/zref)a

(1)

式中：wref和zref分别为参考点速度和高度；幂指数a为地面粗糙度和气温层稳定度的函数。

解决浮力的另外一种方法是利用Boussinesq假设来处理由密度差产生浮力项的影响(如式(2)所示)[11]。这种方法很好地解决了沿垂直高度上的浮力作用。但是这种假设存在缺陷，首先这种假设仅对流体密度变化很小时(β(T-T0)<<1)计算是精确的；其次Boussinesq不能与组分计算同时使用，这就意味着无法描述烟气扩散问题。

(ρ-ρ0)g=-ρ0β(T-T0)g

(2)

式中:ρ0为流体的(常)密度;T0为操作温度;β为热膨胀系数。

为了考虑烟气密度随高度和温度产生的变化[12-14]，本文通过对自然对流理论研究，利用稳态、无内热源、三维、针对可压缩牛顿流体的Navier-Stokes方程，把浮力项加载至动量方程中，动量变化gβΔT是因浮力影响在z方向上产生的。具体形式如下所示：

(3)

(4)

(5)

(6)

(7)

(8)

(9)

本文在同一数学模型中，不仅解决了浮力驱动自然对流的问题，而且解决了烟气扩散的问题。

3 数值结果分析

3.1 空冷塔数值结果

本文所选空冷塔为某一在建空冷塔，该塔塔基地势高度为-80 m，利用已知边界条件进行数值仿真。图3为增加海拔高度压力边界条件的计算结果，地面压力最高为996 Pa。随着高度的增加，压力降低。当高度增加到海拔370 m时，压力降低为-3 788 Pa。利用稳定环境条件下随高度变化的大气压力及浮力模型，可以有效模拟压力随高度的变化。

图3 基于浮力和大气压力影响条件下的压力分布

图4为增加环境侧风5 m/s条件后的流线分布结果。受侧风的影响，塔内的烟气随外部的空气一起向后方移动，而空气受烟气的影响，在靠近塔的位置有所提升，流线向斜上方运动。横向侧风下的烟气流线随着风向及风力有了一定的倾斜角度，增强了空冷塔的烟羽抬升能力。

图4 横向侧风对烟气流线影响

图5给出了5种不同的横向侧风情况下的烟气速度矢量，直观展示出不同大小的横向风速对烟羽抬升以及对烟气流线的影响。横向侧风风速分别取0、5、10、15、20 m/s。结果表明：在横向风速为0 m/s时，烟气垂直地面向上，速度均匀。而随着横向风速的不断增大，烟气流线与烟塔出口角度越来越小，当横向风速达到20 m/s时，烟气几乎平行于烟塔出口排放。

3.2 烟羽抬升高度分析

烟气排放高度对污染物的扩散具有深远影响，排放高度越高，污染物扩散效果越明显，对地面影响越小。所以，近些年来，各国都在研究如何让烟气达到更高的排放高度。烟羽抬升的手段基本有两种方式：一是增高烟囱高度；二是提高烟气抬升高度。增高烟囱高度收效甚微，所以很多国家都致力于研究提高烟羽抬升高度[15-16]。

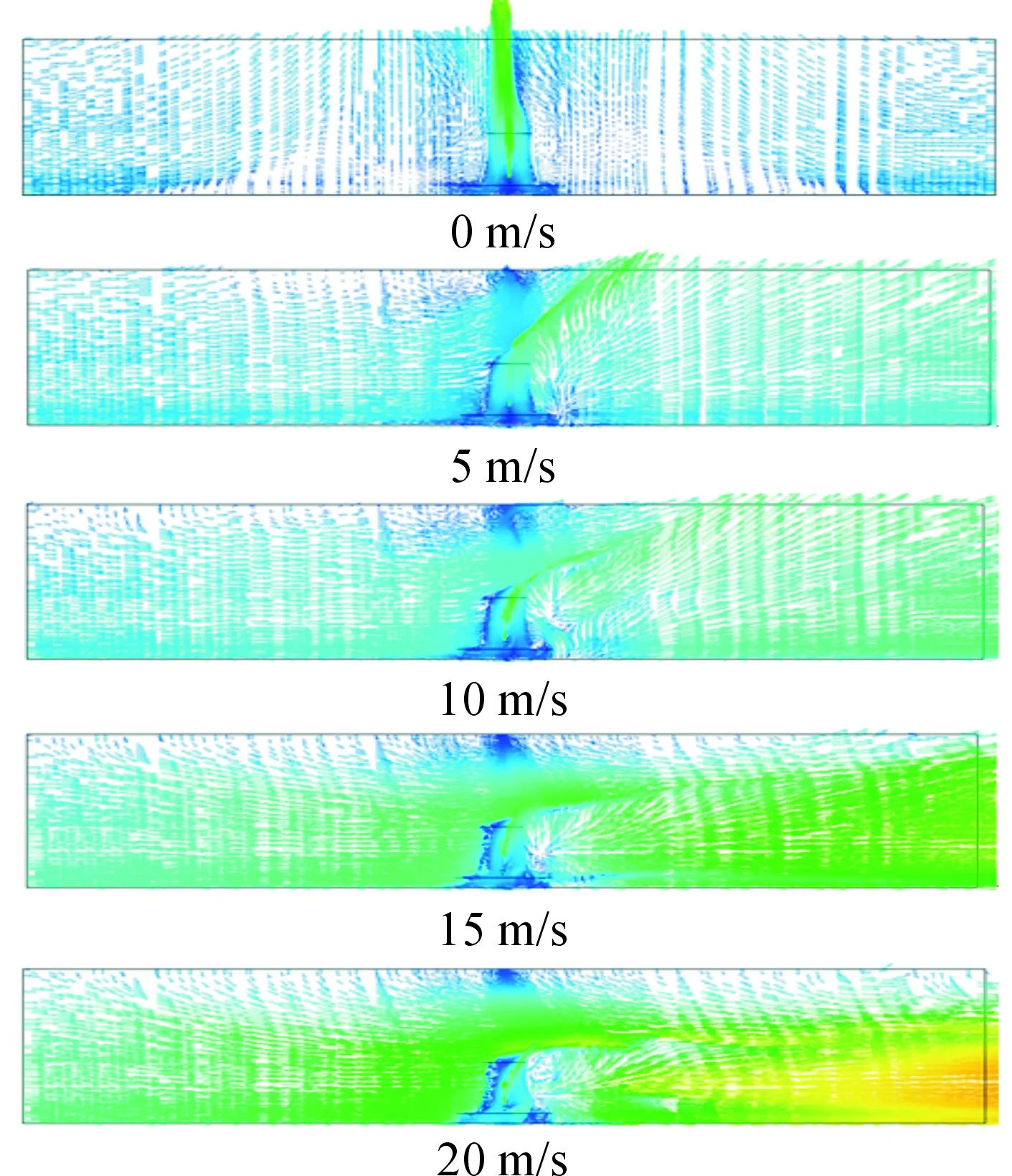
图5 不同侧风下的烟气速度矢量图

环境风速对烟羽抬升高度和烟气在冷却塔内的扩散分布情况有着至关重要的影响。环境风速还与气象环境有着紧密的关系，因此需要对气象环境有所了解，需引入气象学方面的知识。图6为侧风风速分别为0、5、10、15、20 m/s情况下塔内的烟气抬升状况。当横向风速为0 m/s时，烟气垂直地面向上。随着横向风速不断增大，烟气逐渐向后方偏斜。当横向风速达到20 m/s时，烟气几乎不再抬升。

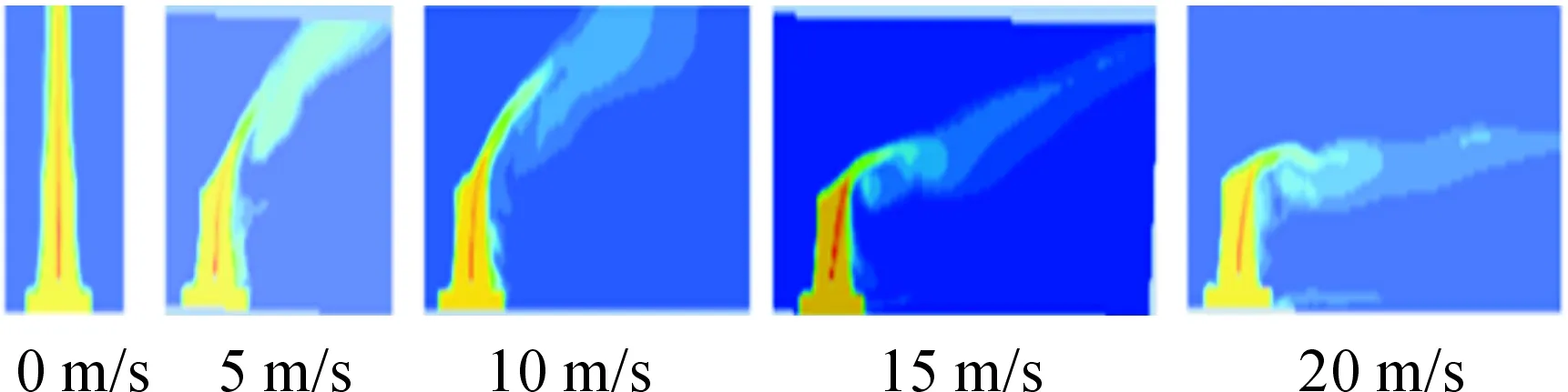
图6 不同横向风速的烟羽分布状态图

本文通过量化的方法研究了环境侧风对烟羽抬升高度的影响。当侧风风速为5 m/s时，烟羽抬升高度最高，可以达到上边界450 m处；当速度达到10 m/s时，烟羽横向偏移了437 m后达到高度450 m；侧向风速增加为15 m/s时，烟羽漂移了1 000 m，烟羽抬升高度为357 m；侧向风速增加为20 m/s时，烟羽在横向漂移到114 m后，即向塔后下方偏转，然后向后漂移，烟羽几乎无抬升，甚至开始因湍流扰动有向塔下移动的趋势(图7)。

图7 不同侧向风速条件下的烟羽抬升高度

随着季节和早晚时差的变化，环境温度也会产生变化，侧向风速在不同环境温度下的影响也会不同，图8反映在不同环境温度下侧向风速对烟羽抬升能力的影响。当侧向风速为5 m/s时，烟羽抬升高度达450 m，横向漂移距离相对较近。当侧向风速为10 m/s时，烟羽抬升高度能达450 m，横向漂移距离增加，特别是当环境温度增高时，横向漂移距离可增加到756 m。当侧向风速为15 m/s时，在横向漂移距离1 000 m的范围内，烟羽最大抬升高度为369 m，环境温度越高，抬升高度越低。当侧向风速为20 m/s时，烟羽抬升高度最低，温度越高，烟羽抬升高度越小。侧向风速大于10 m/s时，烟羽抬升高度随着环境温度的增加而降低。

图8 不同环境温度、不同侧向风速的烟羽抬升高度

3.3 污染物扩散分析

气态污染物扩散是一个三维过程，研究分析污染物的空间浓度分布相比计算最大落地浓度分布更全面。通过下风向不同位置剖面污染物浓度云图可以更清晰地观察污染物在空间的分布，考察不同侧风风速对排烟效果的影响[17-18]。起始剖面为模型下风向50 m处，往后每隔50 m设置一个剖面，共设置4个剖面。

图9是在相同环境温度273 K、相同散热器温度310 K条件下，不同侧向风速空冷塔下游剖面的SO2质量浓度分布。当速度为5 m/s时，SO2质量浓度沿x方向扩散，近塔处浓度较高，远塔处浓度有所降低，SO2浓度随烟羽抬升而相对抬升。在远离塔中心200 m处，SO2浓度依据保持均匀分布状态。当速度增大到10 m/s时，同等浓度SO2分布高度相对变低，浓度分布均匀度变小。当速度增大到15 m/s时，受侧向风速的影响，同等浓度SO2分布区域被扰动，区域分布不再规则。当侧向风速为20 m/s时，受侧向风速的影响，SO2被扰动到塔身区域，开始对塔身结构产生腐蚀影响，增加了塔的运行风险。

图9 不同侧向风速条件下空冷塔下游剖面SO2质量浓度云图

图10是在相同侧向风速10 m/s、相同散热器温度310 K条件下，不同环境温度空冷塔下游剖面的SO2质量浓度分布。前3种条件下的SO2气态污染物扩散程度相似，从图形上来看：283 K工况的扩散程度最优；303 K工况的扩散效果则最差，这种扩散程度差的状态与烟羽抬升高度有一定关系。

图10 不同环境温度条件下空冷塔下游剖面SO2质量浓度云图

4 结论

本文使用CFD数值模拟手段研究在不同环境温度和风速条件下对烟羽抬升高度、污染物扩散的影响关系。结果分析表明：

1) 基于定常、无内热源、三维、可压缩自然对流的牛顿流体数学模型，是解决浮力驱动下自然对流空冷塔的一种有效数学模型。它不仅能描述自然对流的影响，而且能描述多组分烟羽扩散的影响。

2) 利用浮力驱动自然对流的数学模型，可以量化地研究烟羽抬升高度，对获得不同侧向风速下烟羽抬升高度及侧向漂移距离具有重要研究意义。

3) 烟羽提升高度对改善污染物扩散有帮助，较低的环境温度与侧向风速都可以提升烟羽抬升高度，提高污染物扩散程度。

数值结果分析及比对为空冷塔的设计提供了依据。