基于伪谱拼接法的自动泊车路径规划

甘 能,赵克刚,裴 锋,郭泉成,刘素芬

(1.华南理工大学 汽车零部件技术国家地方联合工程实验室， 广州 510640；2.广汽集团汽车工程研究院， 广州 511495； 3.广州南洋理工职业学院， 广州 510900)

随着汽车保有量的增长，停车空间狭窄、停车难等问题日渐凸显。传感器、信息技术、自动化控制理论等的发展为汽车走向智能化奠定了基础。自动泊车作为智能车的重要应用能有效解决入库的问题，越来越受到人们的关注。在泊车过程中通过超声波雷达、摄像头等一系列传感器感知泊车的环境，规划出一条合理有效的避障路线，可有效降低在狭小空间内泊车的难度[1]。

目前，学者们对泊车技术进行了大量的研究。文献[2]采用BP神经网络实现PID控制汽车自动泊车；文献[3]采用神经网络和模糊理论结合的方法进行泊车研究；文献[4-5]采用B样条曲线设计泊车路径；文献[6]采用多段圆弧曲线进行泊车路径设计；文献[7]建立泊车路径规划最优控制问题的数学模型，通过分段离散化为非线性问题，求解出泊车路径。

伪谱法[8-10]在20世纪90年代被引入最优控制领域，该方法的优点是收敛速度极快[11]。伪谱法包括高斯伪谱法(GPM)、切比雪夫伪谱法(CPM)、勒让德伪谱法(LPM)等。Huntington[12]对上述伪谱法进行了研究，并证明LPM和GPM这两类伪谱法在收敛速度和精度上具有优势。本文运用Gauss伪谱法对汽车入库和泊车的路径进行规划计算。

1 狭窄空间下泊车路径规划数学模型

1.1 工况描述

如图1所示，车辆行驶空间狭窄，车辆一次倒车入库极易与周围的车辆发生碰撞。因此，在狭小的空间车辆需要往复多次才能顺利停到车位。

为了解决在狭窄空间的入库问题，把车辆行驶过程分成3个阶段，如图2所示。

第1阶段：车辆后退，从位置A行驶到位置B；

第2阶段：前进到C位置；

第3阶段：挂倒挡行驶，完成入库过程。

这样，车辆在可行驶的狭小空间内多次以不同的转角前进或后退，调整车辆的位置和姿态进行倒车入库，其路径规划可以用伪谱法进行多阶段建模和求解。

图1 狭窄环境下入库碰撞场景

图2 狭窄环境下3次往复入库无碰撞场景

1.2 车辆运动学模型

前轮转向的四轮车符合阿克曼转向几何原理，其运动模型通常可以看成自行车模型。车辆在泊车时，其速度很慢，受侧偏和侧倾等因素影响较小。忽略这些运动学特性，可以把车辆看成在线性空间内运动。如图3所示，以车辆后轴中心的坐标(x,y)来表示，车辆前轮的坐标为(xf,yf)，车辆前后轴的轴距为L,前轮的转向角为δ，车辆朝向与全局坐标的夹角(航向角)为θ，车辆前进速度为v。建立汽车在全局坐标系下位移与车速，横摆角与前轮转角的数学关系。其中x、y、θ为状态变量，δ为控制变量。

图3 车辆运动模型

车辆前轮转角、航向角、车辆横纵向速度之间的关系表示为

(1)

车辆前后轮坐标关系为

(2)

由式(1)(2)可得车辆的运动学约束为

(3)

对于车辆来说，其不仅受到运动学的约束，还受到其他的约束。例如，由于汽车转向器设计的不同，汽车的转向角应约束在一定的范围之内；由于泊车速度相对比较低，其值也应约束在一定的范围之内。

(4)

1.3 车辆与车库建模

1.3.1P-Norm函数的介绍

P-Norm函数可以描绘各种图形，通过选择不同的参数形成不同的图形边界[13]，该函数为

p=1,2,…

(5)

对于式(5)，可以通过取不同的p值得到不同的形状。其中：rx,ry分别为x方向和y方向的比例系数；(a,b)为不同图形的中心坐标。当h(x,y)>0时，点在图形的外面；当h(x,y)<0时，点在图形的里面；h(x,y)=0，点在图形边界上。

不同的p值可以让图形呈现不同的形状。如图4所示，当p=1时函数可以创建菱形；p=2时可以创建圆或椭圆(rx=ry为圆，rx≠ry为椭圆)；当p趋于无穷，图形趋于矩形。

1.3.2车辆边界建模及坐标转化

本文选择某一型号车辆作为研究对象，其基本参数如表1所示。车辆的外形可以看成是一个矩形，在进行车辆建模时，可以采用上述P-Norm函数[10]刻画，选用适当的p值刻画车辆的外形。在车辆坐标系(XC,O,YC)中，为刻画车辆边界，同时减少计算量，在式(5)中取p=4，则变为式(6)，为车辆边界刻画函数，其中：rx、ry分别为车辆长和宽的一半；dr是质心到后轴的距离。则车辆边界上每一个点(XC,YC)都满足式(6)，刻画出的车辆边界见图5。

(6)

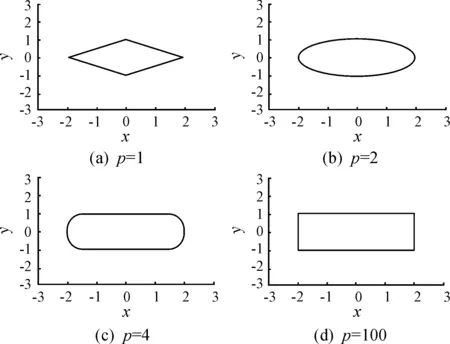
图4 不同p值下的函数图形形状

图5 车辆的近似轮廓

由于智能车在不断地运动，故车辆的边界函数是一个变化的函数。在车辆坐标系(XC,O,YC)中，车辆边界上每一个点(Xci,Yci)可以通过转换矩阵转换成在世界坐标系(x,o,y)上对应的点(xci,yci)，其中车辆位置为(x,y),航向角为θ。车辆坐标和世界坐标的转换矩阵为：

i=1,2,…,4k

(7)

其中(x,y,θ)随时间变化关系由车辆运动学方程(1)表示。

表1 车辆的主要参数

1.3.3车库建模

如图6所示，对于垂直车库函数而言，同样使用P函数进行建模，不同之处在于参数选择，此处不一一列举。车库由最外面矩形h1和左右两边矩形(h2，h3)构成。其中构成3个矩形的P值为6，参数见表2。

图6 垂直车库函数

在世界坐标系中，任意一点(x,y)在车库可行驶区域内满足以下约束条件(称为车库约束条件)：

(8)

1.3.4无碰撞约束条件

为使车辆在入库时不与车库边界发生碰撞，则车辆边界上任意一点(xci,yci)都满足车库约束函数，则无碰撞约束条件为：

(9)

2 多阶段优化问题建立与求解

2.1 多阶段最优问题

车辆在倒车入库时，会受到路面空间、车辆本身尺寸和车辆运动学约束。车辆倒车入库需要大角度的转向，而车辆转向角通常需在一定的范围内，如果进行一次性倒车入库，就会与周围物体发生碰撞，故在狭窄的环境下，采用多阶段倒车入库才能满足车辆尺寸、道路空间和车辆运动学的要求。

进行车辆多阶段倒车入库求解时，由于各阶段的速度方向和各阶段连接时刻车辆的速度变为零，故采取分阶段求解。在第1阶段，车辆的速度为负；在第2阶段，车辆是前进行驶的，故速度为正；在第3阶段，车辆的速度变为负。实际泊车情况下，在每一阶段结束时，车辆可进行原地打方向，此时可以采用分阶段求解。

对于在狭窄空间内泊车这一多阶段最优问题，选择能量最低作为性能指标。对于每一阶段，车辆都应满足车辆运动学约束(如式(3))、车辆的物理约束(如式(4))、车库边界约束(如式(8))、无碰撞约束(如式(9))，以及下面介绍的阶段约束。因此，总的最优控制模型如下：

(10)

(11)

(12)

(13)

(14)

对于第3阶段最优控制问题，还需要添加2个连接约束，使各阶段状态变量连续。

(15)

2.2 基于Gauss伪谱法求解多阶段最优控制问题

针对前文所构建的车辆入库的多阶段最优控制问题，首先可基于Gauss伪谱法的时域变换、状态及控制变量近似、动力学方程转化为代数方程、性能目标函数中积分项转化为求和项等步骤将其转化为非线性规划问题(nonlinear programming problem,NLP)。并应用基于序列二次规划算法开发的NLP问题求解器(如SNOPT、IPOPT)进行数值求解，以获得最优泊车轨迹曲线。具体求解转化过程可参考文献[14]。

3 仿真分析

在PreScan软件中对垂直泊车进行实验仿真，分别得到了车辆位置(x,y)、航向角θ、车辆速度v、前轮转角δ的实验结果。其中车辆位置是质心在世界坐标系的值，航向角是车辆车头方向与x轴的夹角，逆时针为正。仿真结果如图7～11所示。

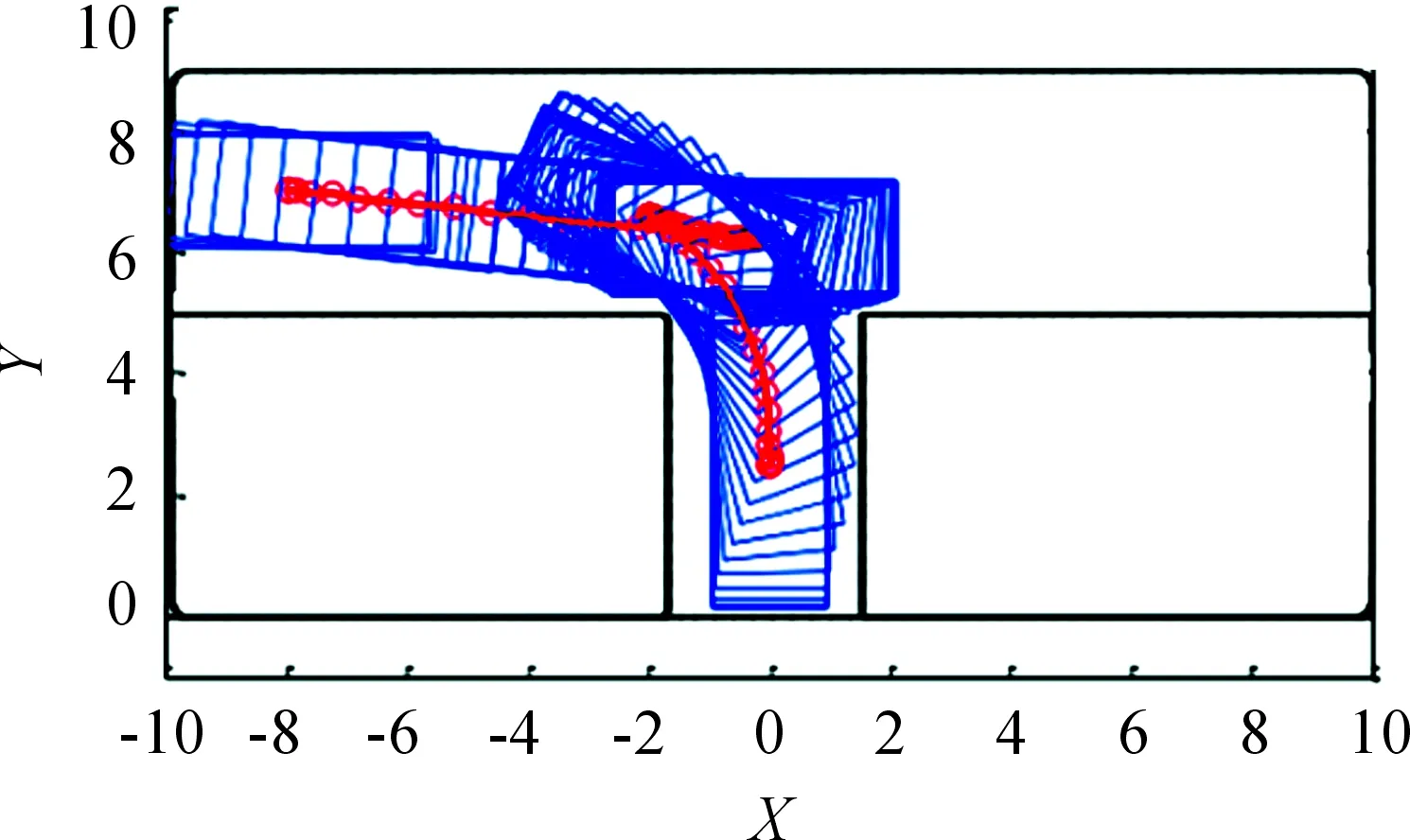
图7 泊车过程仿真示意图

图8 泊车过程中车辆速度的变化

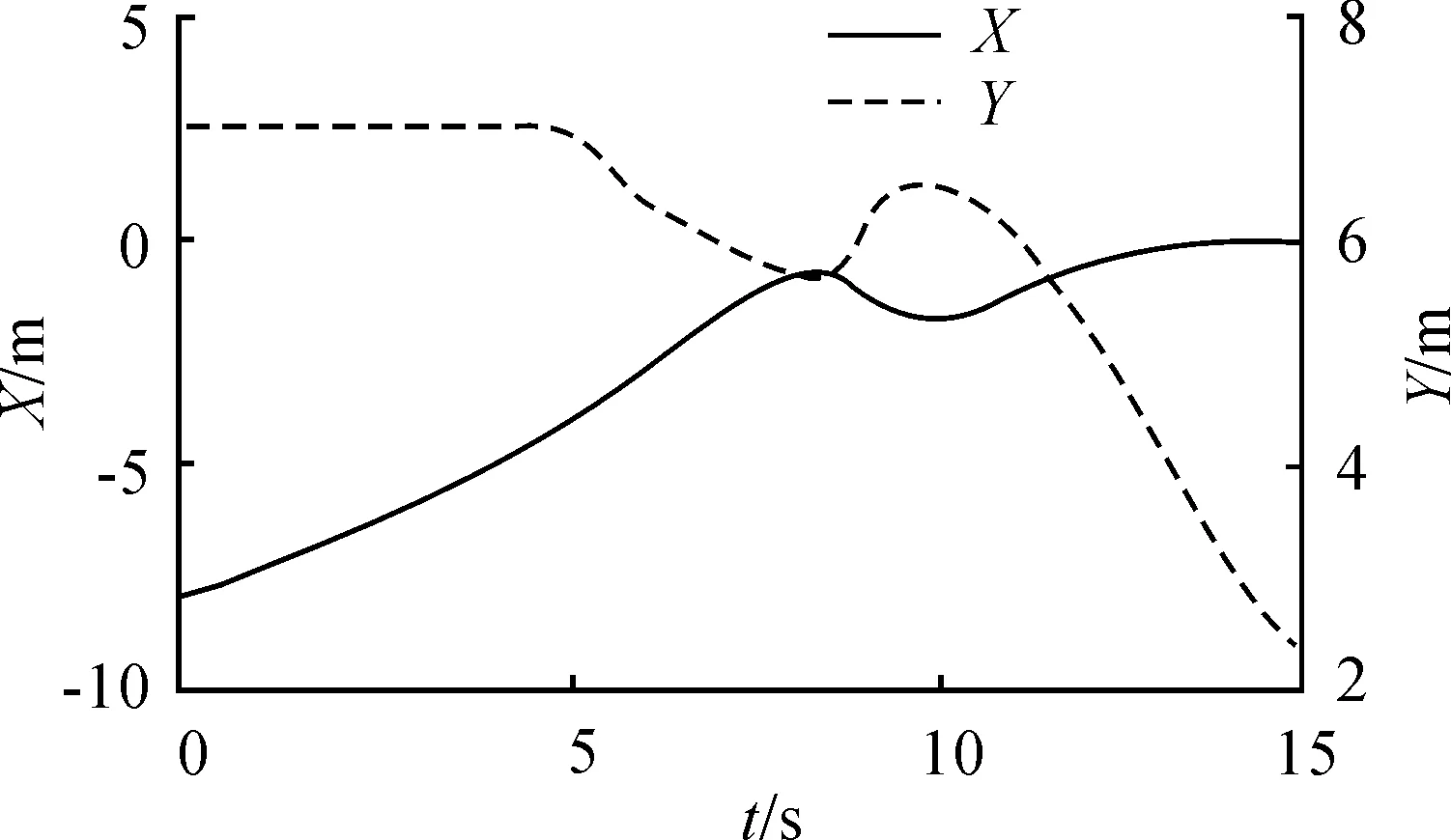
图9 泊车过程中车辆位置的变化曲线

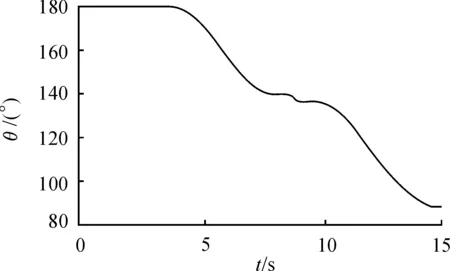
图10 泊车过程中车辆航向角的变化

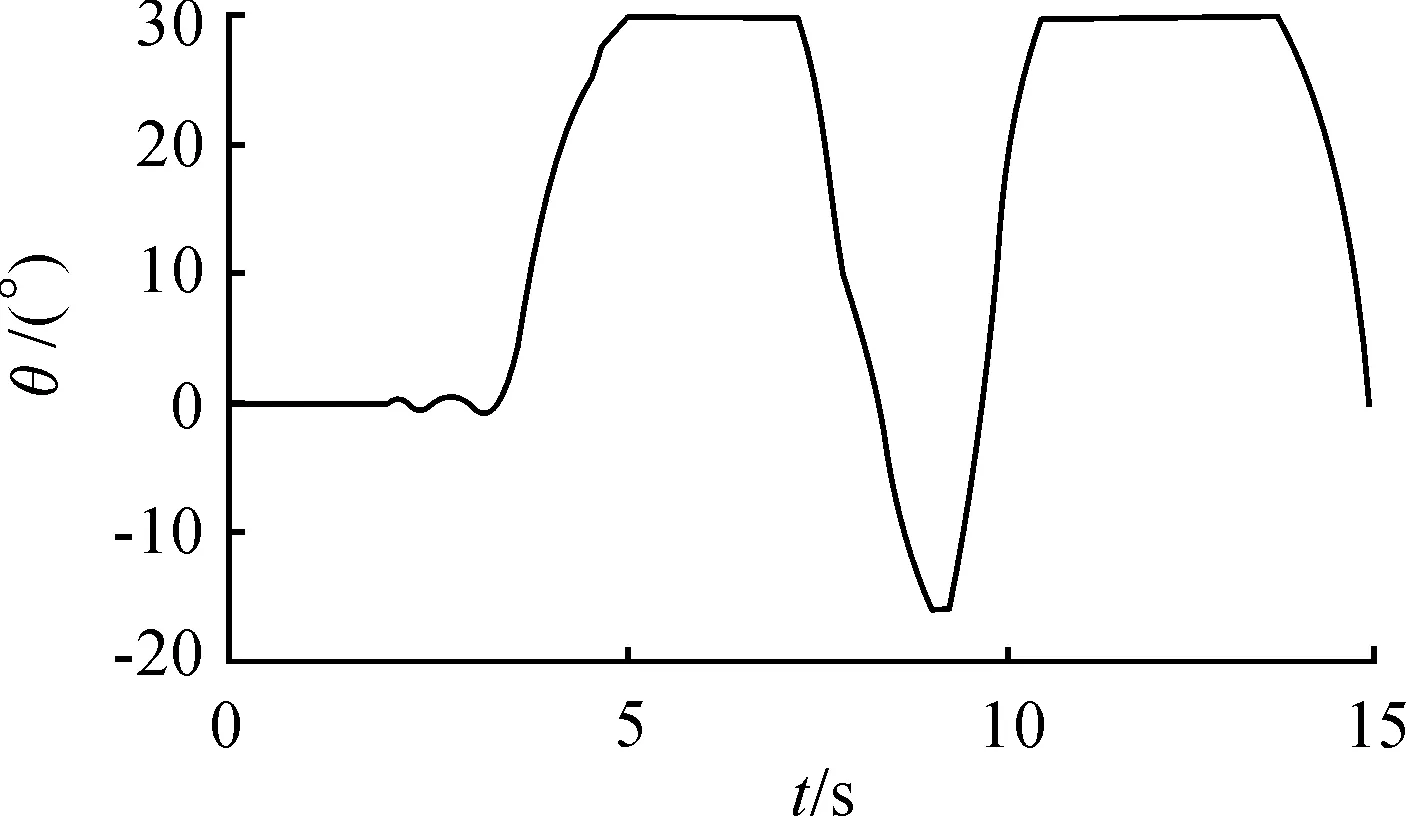
图11 泊车过程中车辆前轮转角的变化

图7为整体的路径规划结果，初始位置x0=-8 m,y0=7 m,θ0=π；末值位置xf=0 m,yf=2.5 m,θf=π/2。由此得到狭窄空间内的泊车路径，该路径分成了3段，符合实际狭窄空间内的泊车结果。

由图8可知，车辆速度先为负，然后变化为正，最后变化为负，对应车辆3阶段的速度变化。在图9中显示了车辆在世界坐标系中的X和Y随时间的变化。在0～8 s内，X随时间的变化而变大，Y先不变然后减小，该阶段为图7的第1阶段，即车辆倒车；在8～10 s内，车辆前进，X减小，Y增大，对应图7的第2阶段；在10～15 s为第3阶段，车辆最终泊车到了(0,2.5)位置。符合泊车要求。图10和图11对应车辆航向角和前轮转角变化，同样符合泊车要求。

4 结束语

为了解决狭窄空间内泊车问题，本文通过P-Norm函数刻画车辆和车库的边界模型，构建运动学方程，结合各阶段的状态来添加各种约束，建立了最优控制模型。然后运用拉格朗日插值，把微分状态方程转换成代数方程，利用高斯积分近似性能积分的积分项，最后运用二次规划法求解最优控制问题。实验结果表明，在狭窄的空间内泊车时，运用高斯伪谱法能较好地规划出路径，为多阶段的最优控制问题提供参考。