基于改进型人工势场的路径规划方法
2019-05-22
(西北工业大学自动化学院,西安710072)
1 引 言
机器人的路径规划问题一直是机器人领域的一个研究热点,很多学者针对不同环境提出了不同的路径规划算法。这些算法可以被分为经典算法与启发式算法[1]。各个路径规划算法都有其优缺点,所以到目前为止没有一种可以适应所有环境的路径规划算法。
由Hart和Nilsson于1968年提出的A*算法是路径规划问题中较为常用的一个方法[2]。A*算法计算量小、可以得到较优的路径,广泛地应用于游戏、无人机与移动机器人领域[3]。由LaValle 于1998年提出的RRT算法[4-5],可以根据环境中已知信息快速地探索环境,是一种概率完备算法。但是该方法采用随机撒点的方式探索环境,所需时间较长、规划出的路径不是最优,且相同环境下规划出的路径还可能不相同。Fox 提出的动态窗口法[6-7](DWA),不同于其它路径规划算法,DWA考虑了机器人的动力学特性与运动学特性,根据这两个特性得到一系列速度离散值,然后用这些速度模拟接下来一段时间内机器人的轨迹,并采用评价函数评价这些轨迹,选取得分最高的轨迹对应的速度作为下一阶段的速度。DWA数学模型简单,但容易陷入死区。其它常见的路径规划算法还有模拟退火法[8]、Q-learning[9-10]、模糊逻辑[11]、人工势场法[12]等。
人工势场法的基本原理是假定机器人在虚拟力场中运动,其中目标点产生引力场,障碍物产生斥力场,这与电荷在电场中的运动相类似。人工势场法得到了广泛地应用,因为它的数学表达式简单、运算快。但是该方法也有缺陷,比如局部极小值、目标点不可达问题。针对这些缺陷,国内外学者提出了很多解决方法。比如引入虚拟障碍物[13]、将人工势场法与模拟退火法结合[14]、修改力场函数[15-16]等。
本文提出了一种改进型人工势场法。在已知环境中障碍物位置的情况下,当机器人遇到局部极小值或者目标点不可达问题后,仿照DWA 评估路径的方法,首先在机器人当前位置周围按照指定规则选择一系列点,然后对这一系列点进行前向延伸,经过多次延伸之后,会得到多条路径。然后采用评价函数对这一系列路径进行评价。选取评估结果最好的路径对应的路径点作为下一个路径点。重复以上步骤直至机器人逃离局部极小值或者到达目标点。
2 问题描述
2.1 传统人工势场法
在人工势场法中,假设机器人在虚拟力场中运动,虚拟力场由引力场与斥力场组成。同时将机器人视为一个点,因此在规划路径时不需要考虑机器人的大小。
引力场Uatt(q)由目标点产生,其计算式为:
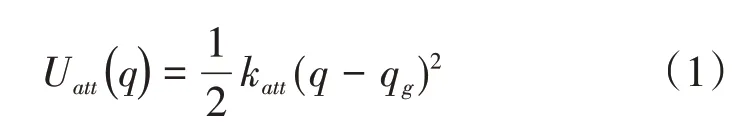
其中katt为引力增益系数,q=(x,y)T为机器人当前位置,qg=(xg,yg)T为目标点位置。斥力场Urep(q)由障碍物产生,其计算式为:

其中krep为斥力增益系数为机器人与障碍物的距离,qobs=(xobs,yobs)T为障碍物位置,ρ0为障碍物的影响距离,当机器人与障碍物距离大于ρ0时,则忽略障碍物对机器人的影响。
机器人所受的合力场U(q)为引力场与斥力场的和,即U(q)=Uatt(q)+Urep(q)。势场函数的负梯度定义为人工力,则计算引力场与斥力场的负梯度可以得到引力Fatt(q)与斥力Frep(q),即

机器人所受合力F(q)为引力Fatt(q)与斥力Frep(q)的和,即F(q)=Fatt(q)+Frep(q)。由于在环境中可能有多个障碍物,因此所受斥力为多个斥力之和,即其中n为障碍物个数。机器人移动方向为所受合力方向,如图1所示。

图1 机器人受力分析Fig.1 Force analysis of robot
2.2 局部极小值与目标点不可达问题
人工势场法由于其数学表达式简单、运算速度快而得到广泛应用,但是其缺陷也是很明显的。人工势场法主要缺陷为局部极小值问题与目标点不可达问题。当机器人所受合力为0或者机器人附近障碍物较多时,机器人容易陷入局部极小值。当目标点附近有障碍物时,可能导致机器人无法到达目标点。
其中局部极小值问题也是在使用人工势场法时最容易遇到的问题。机器人陷入局部极小值分为多种情况。
如图2所示,当机器人、障碍物和目标点位于同一条直线上时。若此时所受合力为0,则机器人停止运动;若合力不为0,则机器人容易陷入振荡。
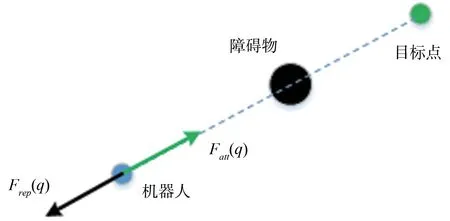
图2 局部极小值第一种情况Fig.2 First condition of local minimum
如图3所示当机器人附近有两个及以上障碍物时,在机器人附近容易形成势阱,此时容易陷入局部极小值。在势阱内部,机器人所受合力将会指向局部极小值点,而机器人此时可能不在局部极小值点,因此此时合力可能不为0。

图3 局部极小值第二种情况Fig.3 Second condition of local minimum
除了局部极小值问题外,人工势场法还面临目标点不可达问题。如图4 所示,当目标点周围有障碍物时,机器人在朝向目标点运动时,也在朝向障碍物运动。因为机器人离目标点越近引力越小,离障碍物越近斥力越大,所以在目标点周围机器人受到的引力较小,而受到的斥力较大。这种情况下易出现目标点不可达问题。
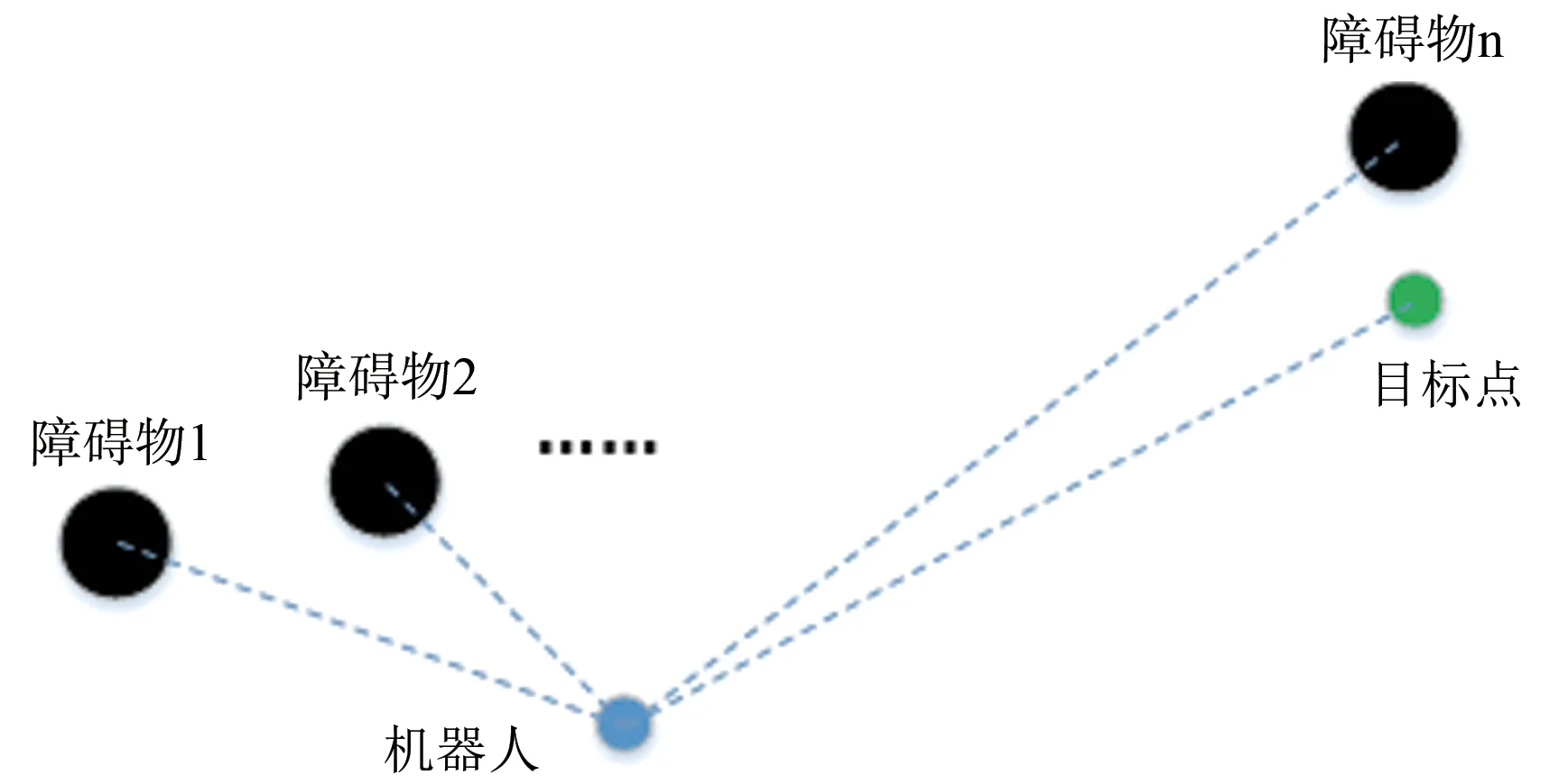
图4 目标点不可达问题Fig.4 Target unreachable
3 基于DWA的改进型人工势场法
3.1 引力场改进
在传统人工势场法中,引力大小与机器人到目标点的距离成正比。当机器人距离目标点较远时,引力会比较大。这就会导致引力在机器人所受合力中占比较大,可能会使机器人忽略障碍物产生的斥力而与障碍物相撞。因此我们使用一种改进型引力场与引力[2]:

其中d0为目标点的影响距离。当机器人与目标点距离较近时,引力大小与机器人到目标点距离成正比;当机器人与目标点距离较远时,引力为常数。这样可以有效地解决机器人离目标点较远时引力较大的问题。
3.2 基于DWA的改进算法
DWA算法是一种经典的路径规划算法,主要思想是:首先根据机器人的动力学与运动学特性,确定机器人在下一阶段的线速度v与角速度ω范围。然后对v与ω进行离散采样,得到一系列速度(v,ω),根据机器人运动学特性对这一系列速度进行模拟,进而得到一系列轨迹。最后采用评价函数对这些轨迹进行评价,选取评价得分最高的一组轨迹对应的速度(v,ω)作为下一时刻的速度。
受DWA 算法的启发,当机器人遇到局部极小值或者目标点不可达问题后,我们在机器人周围选取m个点,然后在这m个点的基础上,再继续选取点。重复以上步骤n次,我们可以得到mn条轨迹。接着采用评价函数对这mn条轨迹进行评价,选取得分最高的一条轨迹对应的点作为下一个路径点。重复以上步骤直至机器人逃离局部极小值点或者到达目标点。
如图5 所示,蓝色点代表机器人,当机器人遇到局部极小值或者目标点不可达问题后,以机器人为圆心,以人工势场法的步长(stepSize)为半径,这样可以得到1 个圆,我们称之为第1 层圆。在第1层圆上均匀地取m个点(图5中的红色点)。然后以这m个点为圆心,以stepSize为半径,可以得到m个圆,称之为第2 层圆。在第二层的每个圆上均匀地取m个点(图5中的黄色点),可以得到m2个点……重复以上步骤n次,便可以在第n层圆上得到mn个点。
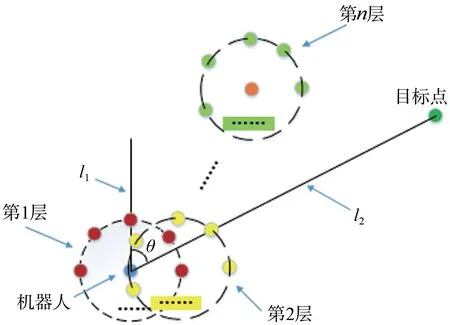
图5 改进型人工势场法原理图Fig.5 Improved artificial potential field method
在得到第1 层圆后,将机器人所在点与第1 层圆上的m个点连接便可以得到m条路径。在得到第2 层圆后,将第1 层圆上的m个点与对应的第2层圆上的m2个点相连,便可以得到m2条路径,此时每一条路径由2 条长度均为stepSize的线段组成。在得到第n层圆后,将第n- 1 层圆上的mn-1个点与对应的第n层圆上的mn个点相连,便可以得到mn条路径,此时每一条路径由n条长度均为stepSize的线段组成。即在得到mn个点后,也即得到了mn条路径。
最后采用评价函数对这mn条路径进行评价,然后选取评价得分最高的一组路径对应的第1层圆上的点作为下一次的路径点,这样机器人下一次前进的距离依旧是一个stepSize。评价函数的设置直接影响最终选取的路径点,因此设计一个合适的评价函数就显得至关重要。下面介绍本文采用的评价函数:

其中每一条路径的总得分为G(x,y),它由两部分组成,即G1(x,y)与G2(x,y),其中:
heading(xi,yi)=(180°-θ)/180°
θ为直线l1与l2的夹角,其中l1由连接第i- 1层上的一个点与第i层上的一个点得到,l2由连接第i- 1层上的一个点与目标点得到。当i= 1时,此时i- 1层上的点即为机器人所在的点。若机器人朝目标驶去,该行为得分很高,而此时θ很小。在仿真环境下,由于(180 -θ)的范围很大,而dist(xi,yi)的范围很小,这就导致G1(x,y)主要由heading(xi,yi)决定,所以我们设计heading(xi,yi)=(180°-θ)/180°。

total(x,y) =tot(x,y)/(n*stepSize)
α、β与γ分别为heading(xi,yi)、dist(xi,yi)与total(x,y) 的权重。在本文中,α、β与γ的值均为固定值,不同的权重参数对应不同的计算结果。比如设置α= 0,即表示不考虑路径点是否朝向目标点,这种情况下得到的路径点将会与障碍物保持一定的距离,但是却可能远离目标点。所以设置合理的α、β与γ就显得尤为重要。
设计G1(x,y)这一项,主要是优先考虑尽可能朝向目标点的路径,但同时机器人也需要与障碍物保持距离;设计G2(x,y)这一项,主要是优先考虑起始点与第n层圆上的点距离较远的路径。但由于随着前向探索的次数增多,需要评价的路径呈指数增长,所以在实际的仿真实验中,尽可能选择较小的n值。
4 仿真实验
仿真环境为MATLAB 2017a,机器人运动在10 × 10 的环境中,机器人的起点与目标点均已知。环境中的障碍物位置也已知,障碍物是半径为0.5的圆。仿真实验分为两个环节:局部极小值问题、目标点不可达问题。有关局部极小值问题的评价指标为机器人在陷入局部极小值后,使用我们的改进型人工势场法后,机器人可以顺利逃离局部极小值点。有关目标点不可达问题的评价指标为目标点附件有障碍物时,使用我们的改进型人工势场法后,机器人可以成功到达目标点。
对于局部极小值问题,一共设置5组实验场景,其中三组为手动设置障碍物,另外两组采用随机数的方式设置障碍物,随机数由MATLAB的unidrnd函数生成,为离散均匀随机数。对于目标点不可达问题,设置2组实验场景,障碍物为手动设置。表1是实验参数设置。

表1 参数设置Table1 Parameter setting
4.1 局部极小值实验结果
在前三组实验中,手动设置障碍物得到三组不同的实验场景,如图6~8 所示。在每幅图中,左边部分为传统人工势场法,右边是改进型人工势场法。在三组仿真实验中,起点位置分别为(0,0)、(0,0)和(9,0),目标点位置分别为(6,6)、(9,9)和(1,9)。在改进型人工势场法中,在无人车陷入局部极小值后,采用改进型算法,规划出的路径为图中绿色路径,其他情况下使用传统人工势场法,规划出的路径为图中蓝色部分。在三组场景中,机器人均遇到了局部极小值,在使用了改进型人工势场法后,机器人均可以成功逃离局部极小值,这说明我们的改进型人工势场法可以有效解决传统人工势场法中面临的局部极小值问题。
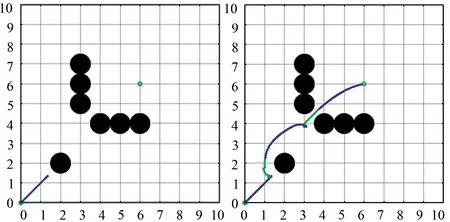
图6 场景一Fig.6 Condition 1

图7 场景二Fig.7 Condition 2

图8 场景三Fig.8 Condition 3
在以上三组实验的基础上,再增加两组随机试验,在已知起点与目标点位置的情况下,随机设置障碍物。在图9 两组随机试验中,机器人经过由多个障碍物构成的狭窄通道时,陷入了局部极小值,然后调用改进型算法,成功逃离局部极小值,说明改进型人工势场法适用较为复杂的静态未知环境。

图9 随机障碍物Fig.9 Random obstacle
4.2 目标点不可达实验结果
针对目标点不可达问题,设置两组不同实验场景。如图10 与图12 所示,目标点周围有几个障碍物,在使用传统人工势场法后,机器人无法到达目标点。在图11 和图13 中,机器人检测到目标点附近有障碍物后,启用改进型人工势场法,顺利到达了目标点,说明改进型人工势场法可以解决目标点不可达问题。
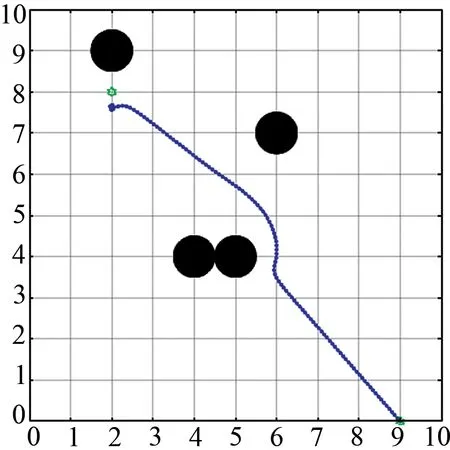
图10 传统人工势场法Fig.10 Traditional artificial potential field method
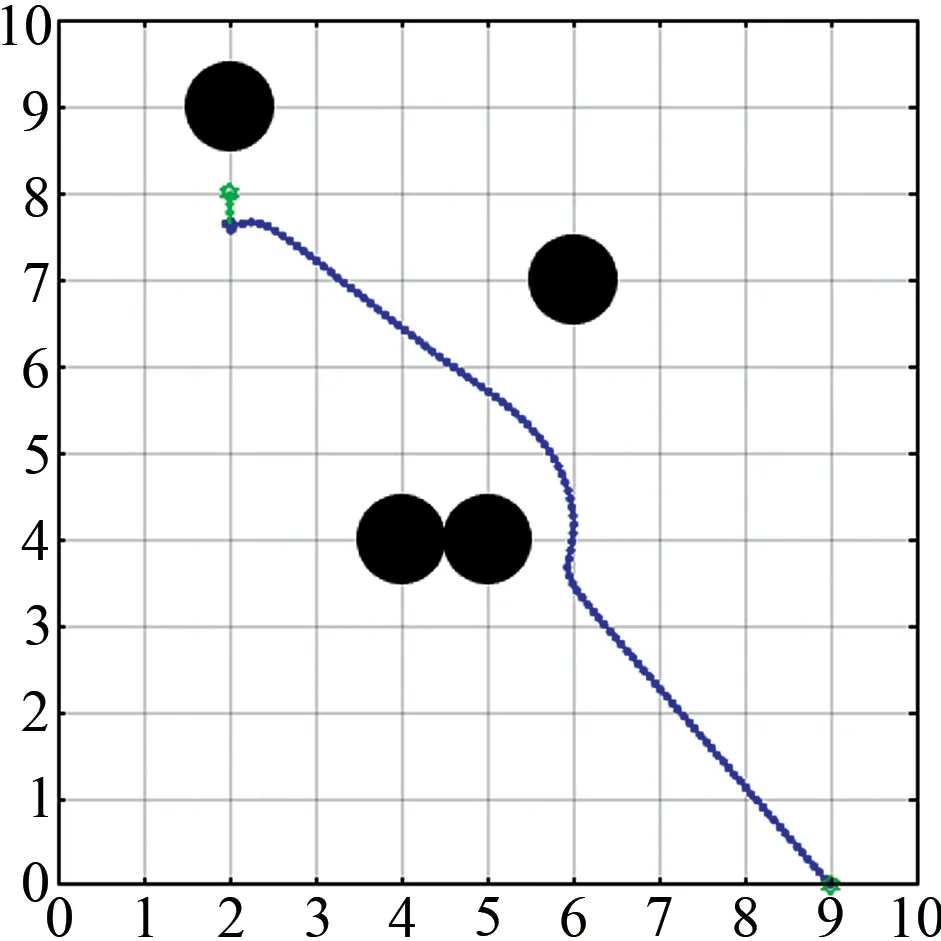
图11 改进型人工势场法Fig.11 Improved artificial potential field method
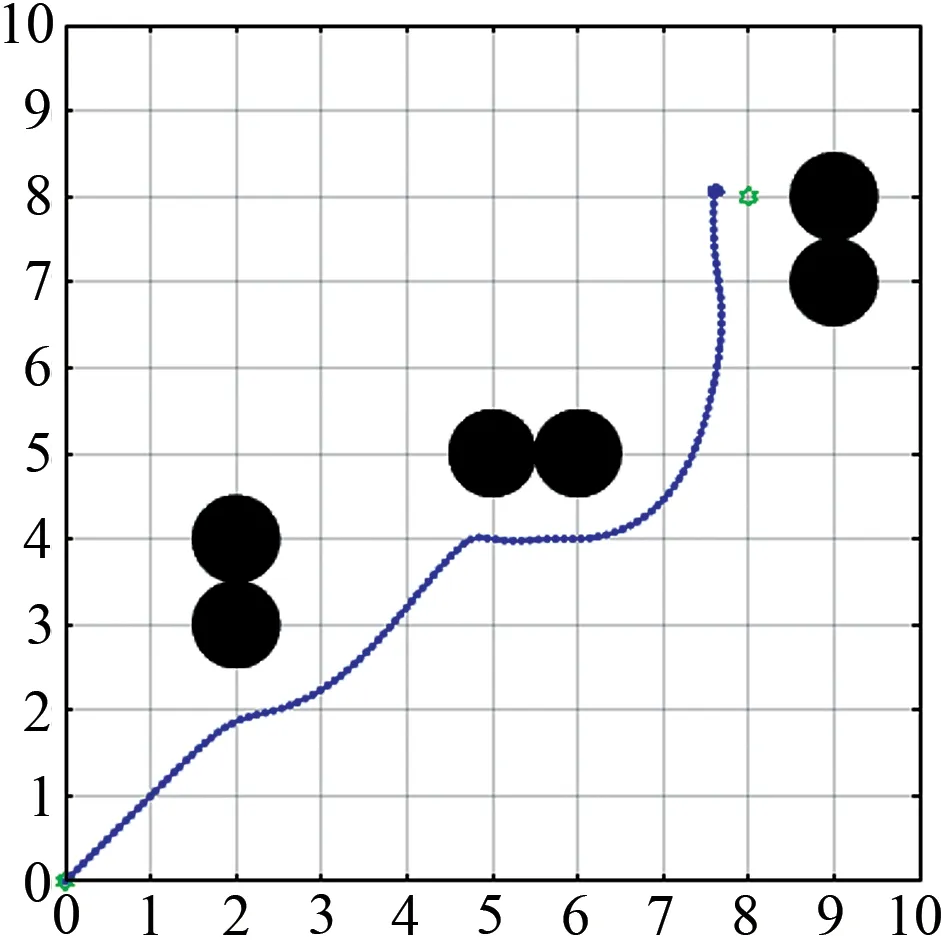
图12 传统人工势场法Fig.12 Traditional artificial potential field method

图13 改进型人工势场法Fig.13 Improved artificial potential field method
5 结 论
在使用传统人工势场法时,容易遇到局部极小值和目标点不可达这两个问题。针对以上问题,本文提出了基于DWA 的改进型人工势场法。仿真实验结果表明,我们的改进型人工势场法可以解决传统人工势场法面临的局部极小值和目标点不可达问题。在未来的工作中,本文将会加入动态障碍物规避以及在实际机器人上进行实验。
