无人机下投探空仪投放过程数值模拟

肖良华，闫林明，曹世坤，郭 然，陈 斌

（1. 航空工业成都飞机工业（集团）有限责任公司，成都610092；2. 中国气象局气象探测中心，北京100081）

1 引 言

利用飞机进行下投探空，可对大气温度、压力、湿度和风速风向等气象要素的垂直分布进行高分辨率测量，为台风的监测和预报提供数据支持，因此具有极其重要的实际应用价值。考虑到台风的特点及其探测的风险，高空长航时无人机是下投探空的首选平台[1-2]。为此，成都飞机工业（集团）有限公司基于自主研制的云影无人机平台设计了机载下投探空系统[3]。

在具体投放中，探空仪按照一定的时间间隔从无人机翼下吊舱尾部投出。类似“弹类”物体从飞机上的投放，探空仪的投放也需要开展安全性分析，以避免其投出后同飞机机体或尾翼发生碰撞。一般可以通过风洞试验或者数值模拟的手段来研究探空仪投放过程。试验方法有动力相似法、捕获轨迹法和网格法[4]。由于探空仪重量轻、尺寸小，轨迹法和网格法试验难度大，而基于动力相似法的缩比试验又难以保证弗劳德数（Fr）等参数的相似，如同时满足重量、惯量及重心要求比较困难[5]，因此总体而言试验方法难度大、成本高。数值模拟则可以以较低成本、按照真实尺寸开展研究。

探空仪投放过程的数值模拟需要通过非定常流场的模拟来获得气动力，然后将气动力代入动力学方程中求解其速度及角速度，最后通过运动学方程积分获得运动轨迹及姿态。显然，气动力的求解尤为关键。投放过程中，探空仪同载机的相对位置一直在变，流体域的求解网格需要随之变化。目前针对探空仪投放过程的数值模拟鲜见报道，其具体模拟方法可以参考“弹类”物体从飞机上分离的数值模拟。如张启南等[6]基于面元法和工程估算法的气动力获取方法开发了外挂物与载机分离过程的数值模拟系统。李孝伟等[7]利用动态嵌套网格技术，通过求解Euler 方程和六自由度动力学方程，模拟了副油箱从飞机上的投放过程。Deryl 等[8]、冯文梁等[9]采用基于Euler 方程的方法，模拟了武器外挂物的投放过程，模拟结果同风洞试验结果吻合较好。杨磊[10]、杜小强[11]通过求解雷诺平均Navier-Stokes（RANS）方程获得气动力，分别模拟了机载武器投放过程和其流动特性。可见随着计算能力的提升，气动力获得方法越来越复杂，也越来越准确。

同时，同“弹类”物体相比，探空仪的“密度”（重量同其外壳所占流体域体积之比）小得多，从而导致气动力在投放过程中的作用更加突出；转动惯量小、稳定性较低，导致探空仪姿态更容易发生变化，因此对气动的模拟需要更加小心。而且探空仪为钝头体外形，开口端流动分离严重，流场模拟难度大。

为此，本文采用动态嵌套网格技术，通过非定常RANS 方程的求解获得气动力，来实现探空仪投放过程的数值模拟。利用模拟结果分析了探空仪的运动及其受力变化过程。最后，为了评估流体粘性对模拟结果的影响，采用欧拉方法开展了同样的数值模拟。

2 物理模型

2.1 模拟对象

模拟对象包括带吊舱载机和探空仪。载机为云影无人机，其模型如图1 所示，取坐标系O-XYZ，坐标原点为机头位置，X轴为机体轴指向后，Z轴在对称平面内指向上，Y轴指向右，构成右手坐标系。模拟中，载机固定不动，可选坐标系O-XYZ为惯性坐标系。

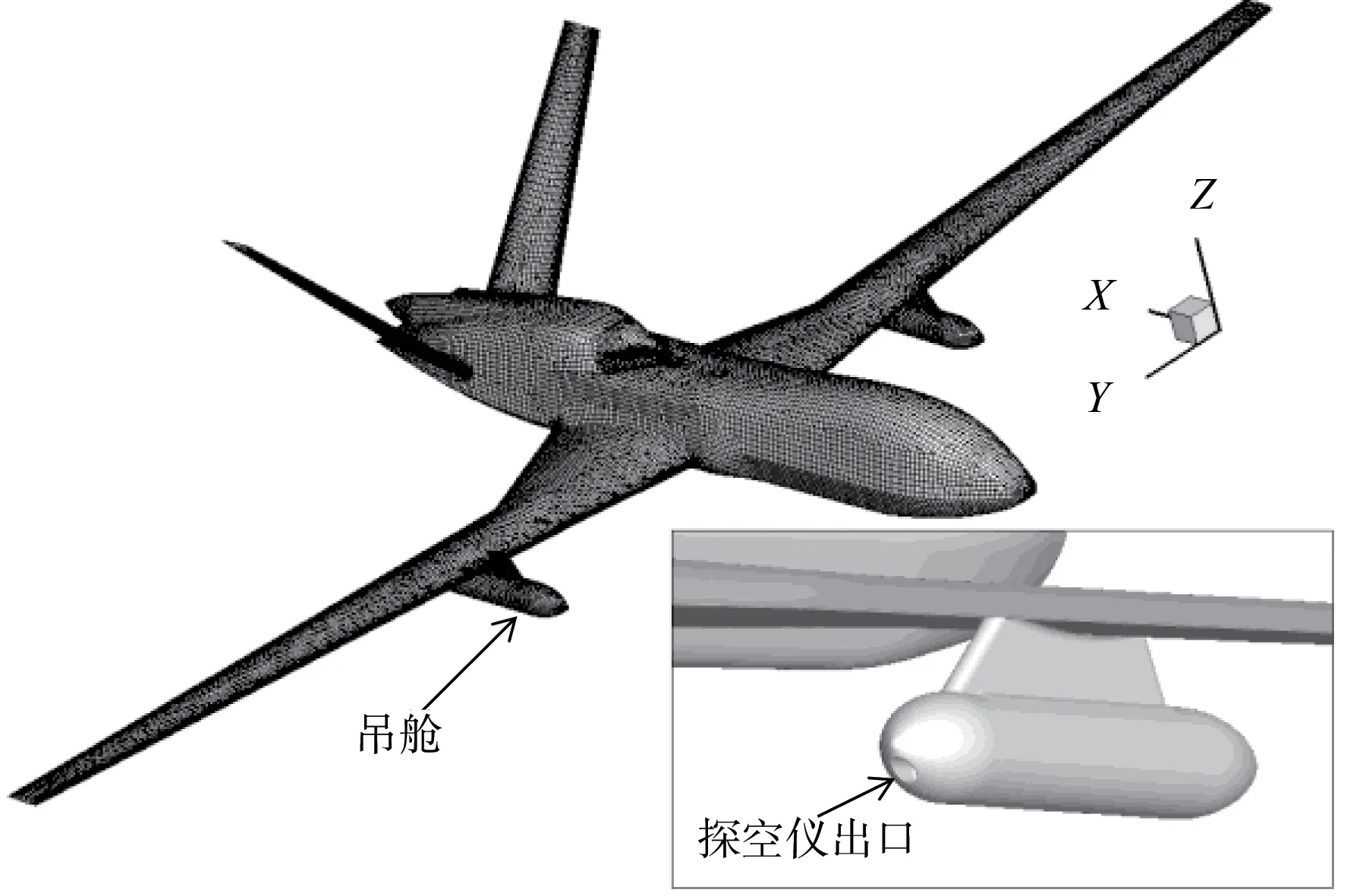
图1 云影无人机模型及表面网格Fig.1 Model and surface mesh of Cloud Shadow unmanned aerial vehicle

探空仪模型如图2所示，整体呈圆柱形，开口端内安装有传感器（数值模拟的模型中忽略了内部的传感器），开口端的外支架可对传感器起保护作用；封闭端内安装有降落伞等。投放时开口端先出舱，因此封闭端为迎风面。为方便后续分析，建立如图2 所示探空仪固连坐标系O1-X1Y1Z1，原点O1为探空仪质心，X1轴穿过探空仪轴线指向后，Y1轴及Z1轴与X1轴垂直，且构成右手坐标系。探空仪直径D为65mm，总长L为350mm，其中开口段长24.8%L，质量为380g，重心距离封闭端长34.4%L。

2.2 非定常RANS方程

采用雷诺平均N-S 方程求解流体域，非定常可压缩RANS方程在直角坐标系下积分形式如下：

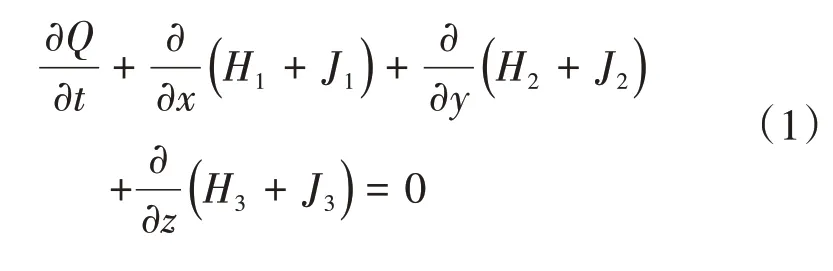
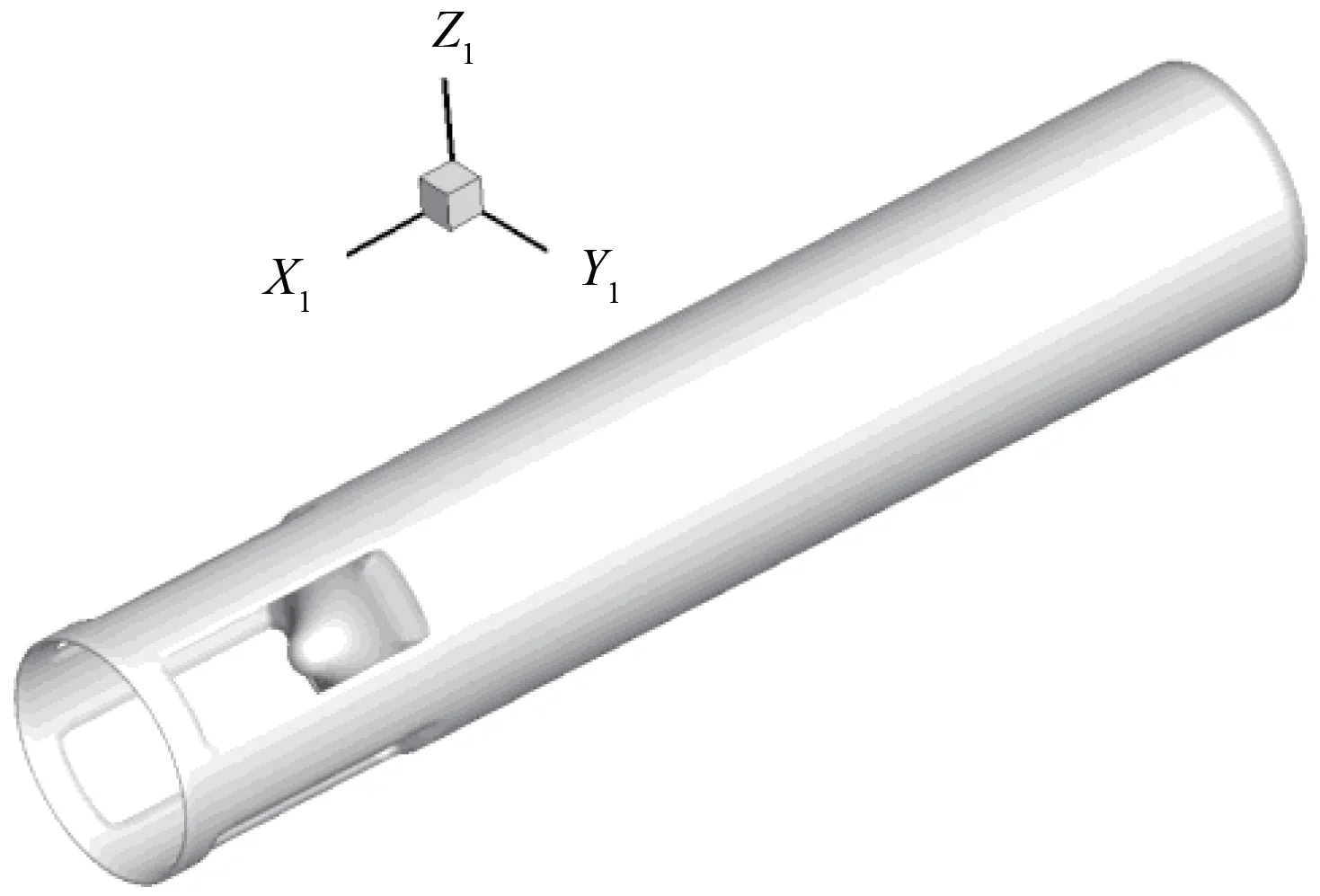
图2 探空仪模型Fig.2 Model of dropsonde

其中，ρ为空气密度，p为压力，u，v，w分别为气流在x，y，z方向的速度分量，e为内能，H1，H2，H3为无粘通量，J1，J2，J3为粘性通量，τij(i，j=x，y，z)为切应力张量，包含分子粘性应力和雷诺应力。雷诺应力项需要通过湍流模式来封闭，在模拟中采用可实现的k-ε湍流模式[12]。

2.3 六自由度动力学方程

探空仪投放后在气动力和重力的作用下自由运动，其运动遵循六自由度动力学方程，该方程在探空仪固连坐标系O1-X1Y1Z1下的表达式为[13]：

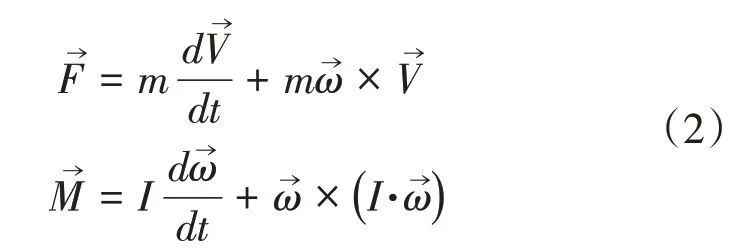
其中，F→为探空仪受到的合力，包括重力和气动力；M→为探空仪所受相对质心的气动力矩；V→、ω→分别为探空仪相对惯性坐标系O-XYZ的速度和角速度，即相对于载机的速度和角速度；I为探空仪在质心位置取的转动惯量，由于对称性，惯性积Ixy=Ixz=Iyz=0，转动惯量

Ixx=1.93×10-4kg ⋅m3，Iyy=Izz=27.3×10-4kg ⋅m3。

通过式（1）迭代求解流体域，可以获得探空仪所受气动力，将气动力带入式（2），进而可求得探空仪相对惯性坐标系O-XYZ的速度和角速度，然后通过时间推进求解运动学方程获得下一时刻探空仪质心位置及姿态角，其中姿态采用欧拉角偏航角Ψ、俯仰角Θ和滚转角Φ表示，以更新后的相对位置重复上述步骤，即可获得探空仪投放过程运动轨迹。

3 数值模拟方法

3.1 动态嵌套网格方法

动态嵌套网格方法具有网格生成简单、易于描述不同物体之间的相对运动的优点，非常适合投放过程数值模拟[10]。

模拟中，分别生成载机网格（背景网格）和探空仪网格（子网格）。载机网格为静止网格，其表面网格如图1 所示，计算域取为20 倍机身长度，非结构网格总量约为一千万，其中对探空仪运动过程中可能出现的区域进行了加密处理。

探空仪网格为动态网格，即探空仪网格相对探空仪静止并随探空仪一起运动，网格如图3所示，网格量为110万，在开口端尾迹区进行了加密。

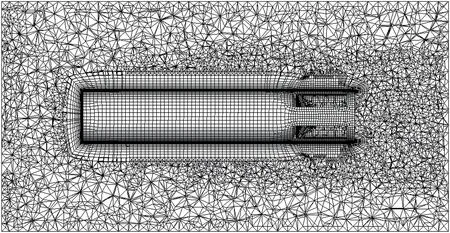
图3 探空仪网格Fig.3 Mesh of dropsonde

一般情况下，使用探空仪网格外边界切割载机网格，在切割边界上进行传值，即可使整个流场域实现非定常流场模拟。当探空仪距离吊舱很近时（如图4），探空仪网格同吊舱物面相交，此时需在切割载机网格前，先利用吊舱物面切割探空仪网格形成BC_cut0，如图5红色粗线所示，继而利用BC_cut0和探空仪网格剩余外边界一起切割载机网格，形成BC_cut1（图4中蓝色中等粗线）。

图4 网格切割边界Fig.4 Boundary of grid cutting

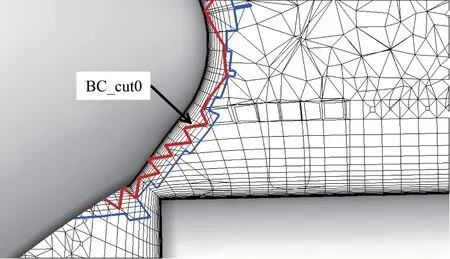
图5 网格切割边界局部放大图Fig.5 Partial detail of grid cutting boundary

由于在模拟中的不同时刻，两套网格的相对位置不同，因此网格的切割在每个时间步中都需要进行。

3.2 其他

在CFD++软件的数值模拟中除了采用动态嵌套网格方法外，空间离散采用二阶Total Variation Diminishing（TVD）格式，时间推进则采用双时间步隐式推进方法，并采取多重网格加速措施。

边界条件上，远场设置为基于特征值的进出口边界，来流马赫数（Ma）为0.5，飞行高度设置为10km，攻角为-2°，侧滑角为0°。物面边界均设置为绝热无滑移壁面。

实际投放中，探空仪以一定出射速度从吊舱中弹出。为方便仿真计算，将探空仪刚离开吊舱的状态设为初始状态，且假设此时探空仪轴线与吊舱轴线平行，出射速度沿探空仪轴线方向，大小为1m/s，初始时刻探空仪位置如图4所示。由于探空仪出口轴线同X-Y平面成-1.2°夹角（迎风端朝下），因此探空仪初始姿态欧拉角Θ=-1.2°。数值模拟时，先通过定常模拟获得初始位置的稳定流场，以便为自由运动模拟提供初始流场，然后开启探空仪六自由度运动和非定常模拟。

4 仿真结果及分析

4.1 非定常模拟收敛性验证

非定常时间推进过程中，随着探空仪的运动，流场不断变化，因此一方面需要确保流体域求解的收敛，另一方面需要时间推进步长足够小，以保证探空仪运动轨迹积分过程的精确度。因此，为衡量非定常计算中的收敛情况，首先开展了不同子迭代步数和不同时间步长的数值模拟。

子迭代步数分别取为10 步和15 步，模拟所得探空仪轨迹及姿态角分别如图6、图7 所示，其中位移以探空仪长度L无量纲化处理。可见，两个模拟所得的探空仪轨迹吻合很好，欧拉角差别也很小，尤其是偏航角和俯仰角吻合很好，而滚转角对探空仪气动力影响小，因此为了兼顾计算效率，在模拟中选择子迭代步数为10。

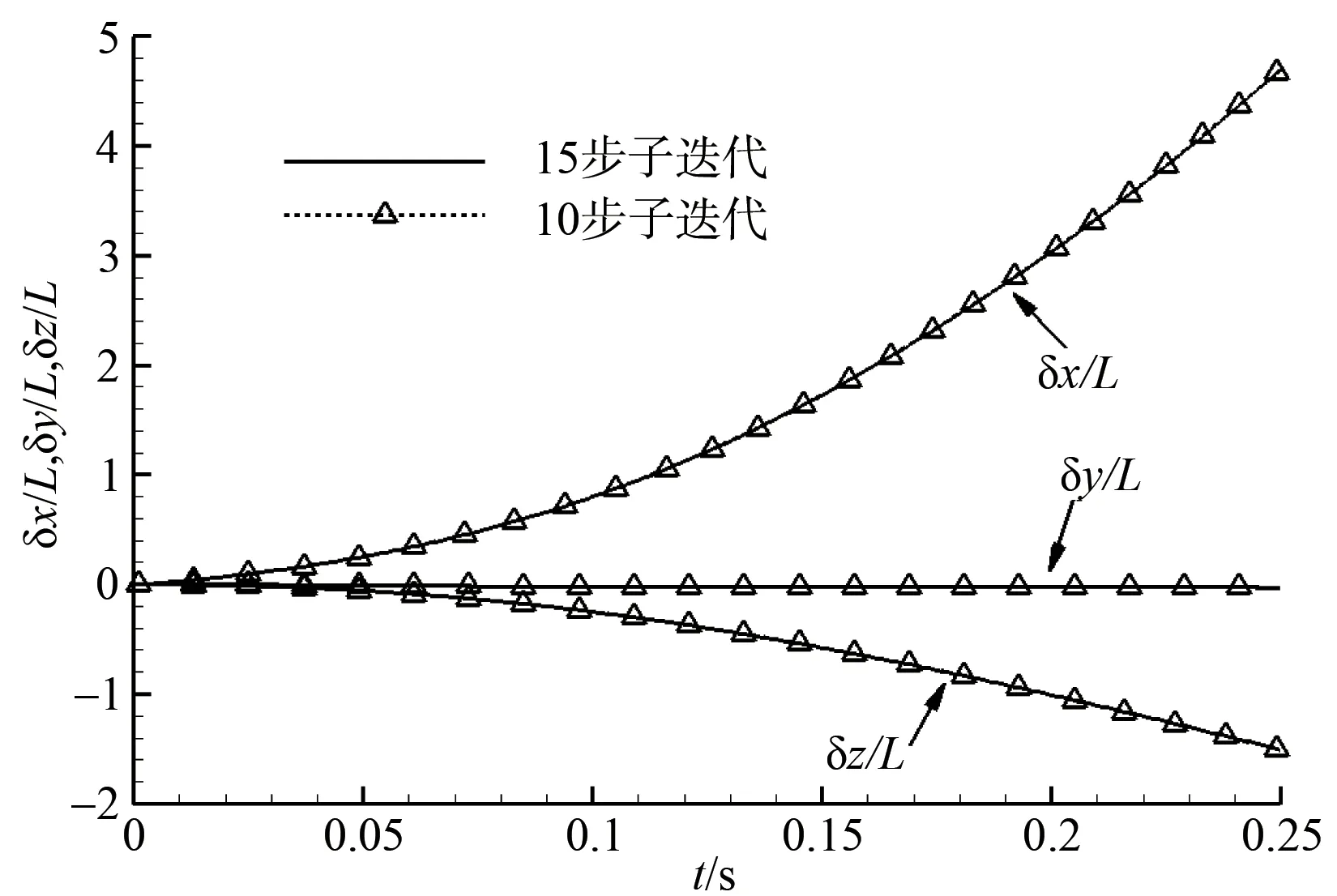
图6 不同子迭代步数模拟的探空仪轨迹Fig.6 Dropsonde trajectory of simulations with different sub-iteration steps

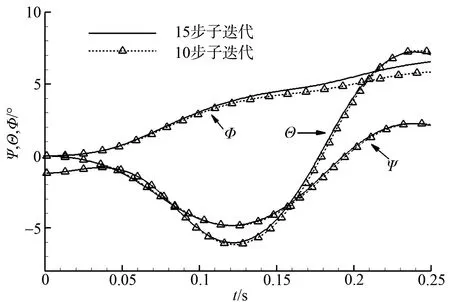
图7 不同子迭代步数模拟的探空仪欧拉角Fig.7 Dropsonde euler angle of simulations with different sub-iteration steps

在子迭代步数取为10的基础上，选取时间步长分别为0.002s、0.001s和0.0005s，模拟所得探空仪轨迹及姿态角分别如图8、图9 所示。可见，不同时间步长模拟所得的探空仪轨迹吻合很好，而姿态角存在一定的差别。当时间步长大于0.001s时，姿态角的差别较为明显，而时间步长小于0.001s 时，姿态角的差别较小，因此在一般模拟中选择时间步长为0.001s。

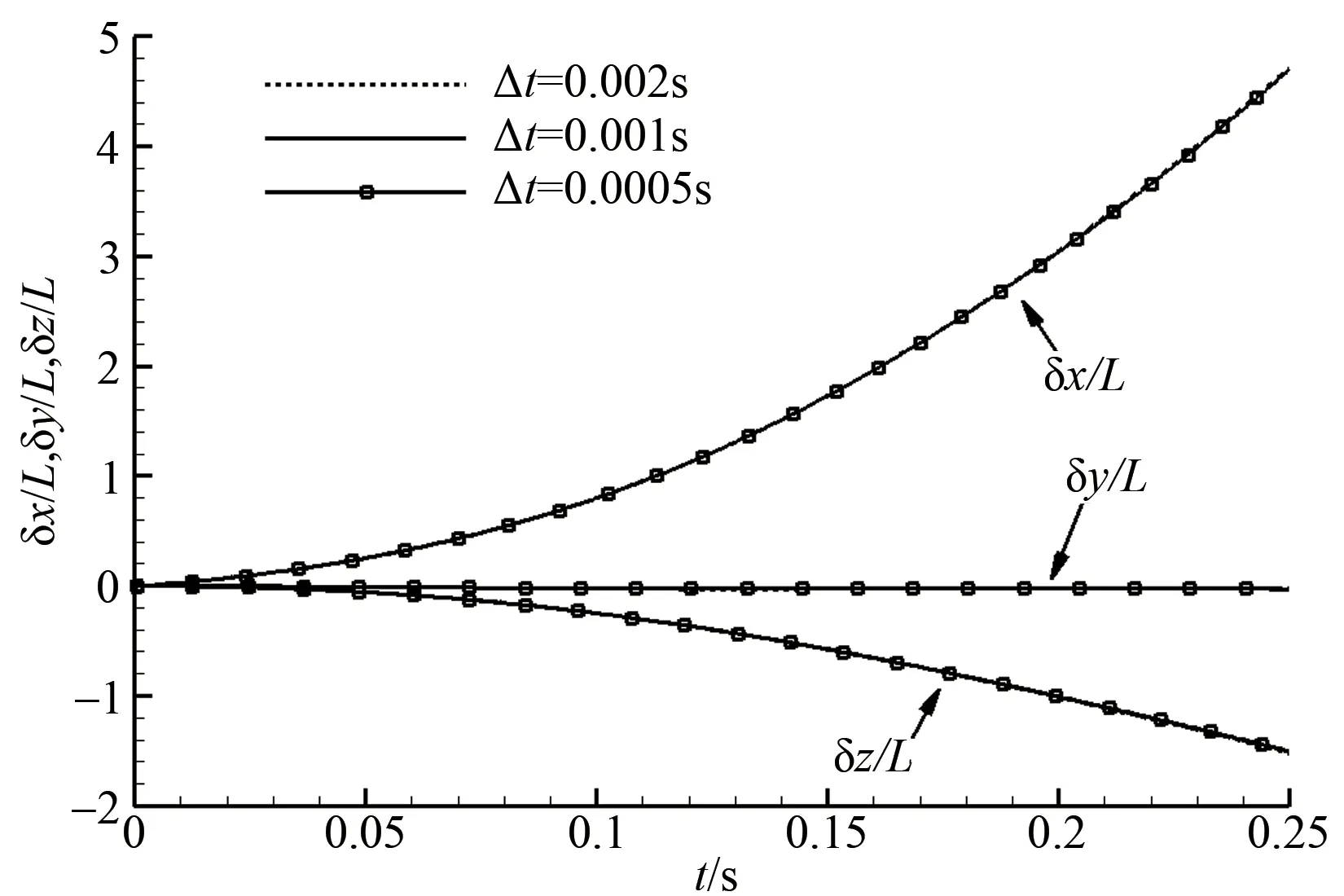
图8 不同时间步长模拟的探空仪轨迹Fig.8 Dropsonde trajectory of simulations with different time step lengths

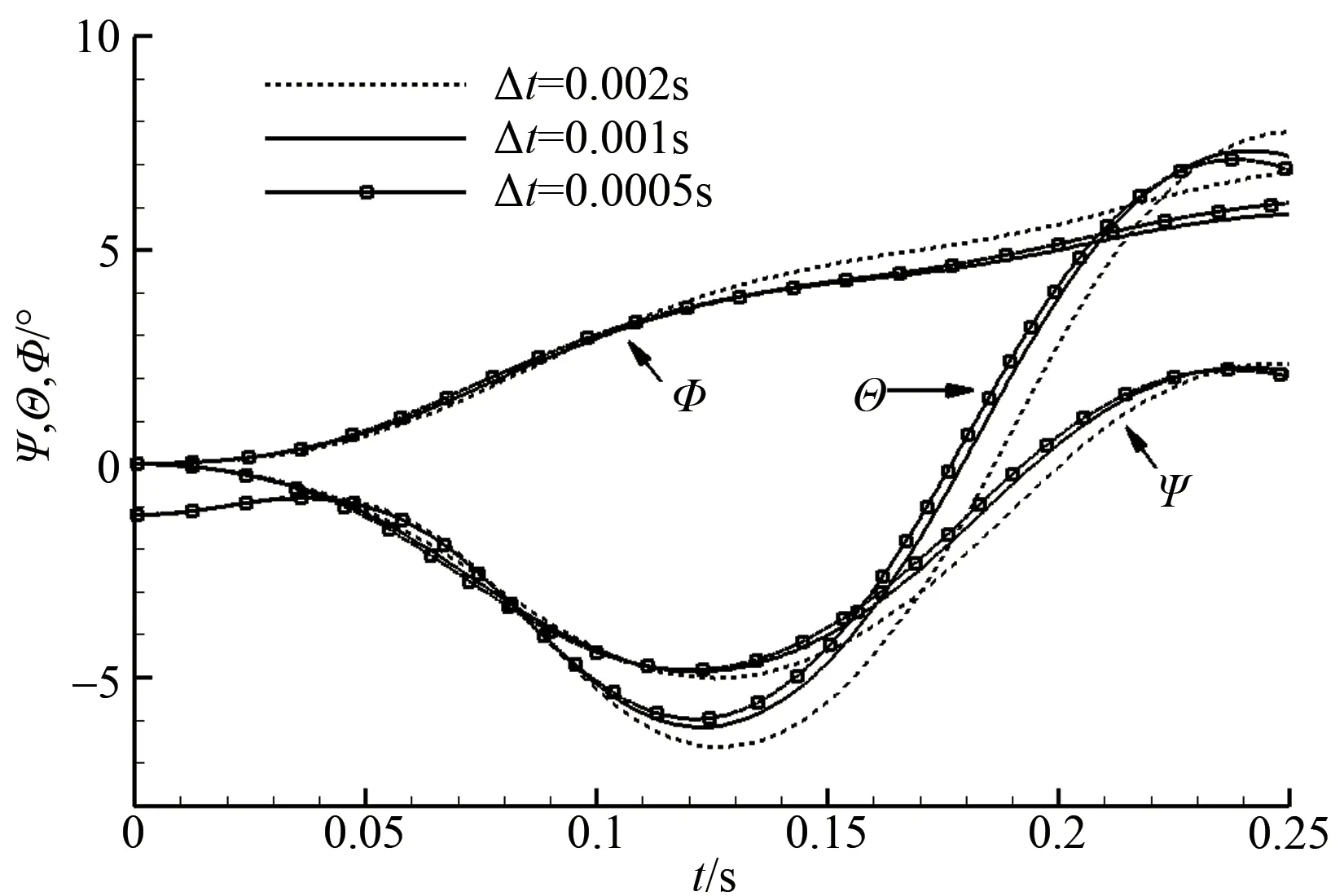
图9 不同子迭代步数模拟的探空仪轨迹Fig.9 Dropsonde euler angle of simulations with different time step lengths

4.2 探空仪运动分析

基于子迭代步数为10、时间步长为0.001s的数值模拟结果，作出不同时刻探空仪运动位置图，如图10 和图11 所示。投放过程中，探空仪主要在流动方向（向后）和重力方向（向下）运动，且流动方向运动速度明显大于重力方向。而一般的“弹类”物体的投放过程中，其运动主要体现在重力方向。可见，探空仪这类轻质物体的投放过程受气动力的影响更为明显。这也是本文选择RANS方程而非欧拉方程求解流体域的原因（4.4 节中进一步对比了RANS方法和欧拉方法模拟的结果）。

投放过程中，探空仪未出现翻滚，姿态角变化范围不大，可见由于开口端的存在，使得探空仪气动力作用点处于重心之后，从而具有一定的稳定性。探空仪离开吊舱0.2s 后则已经脱离无人机机尾，因此数值模拟中只模拟0.25s时长。

图10 不同时刻探空仪位置（侧视图）Fig.10 Dropsonde release events(side view)

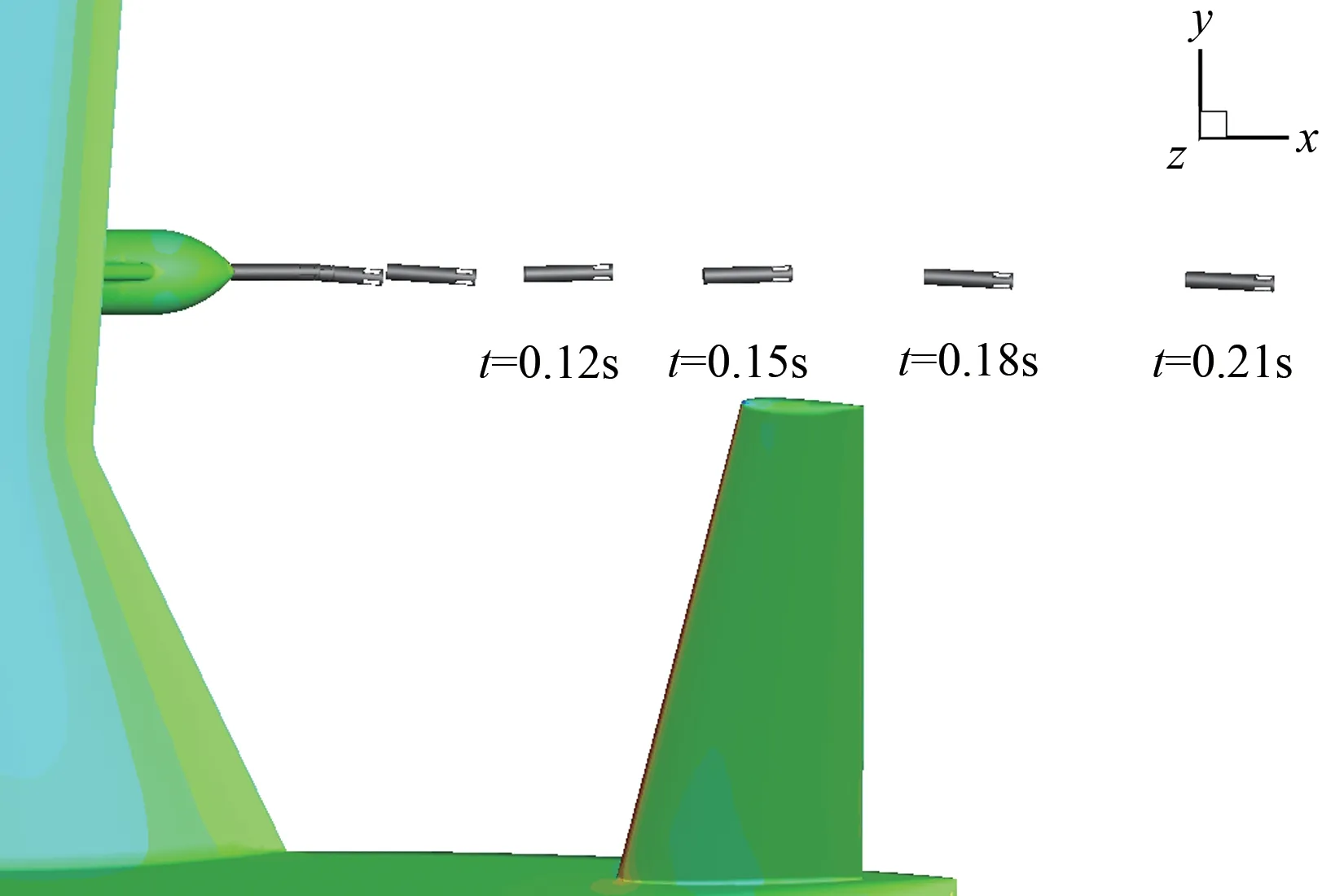
图11 不同时刻探空仪位置（俯视图）Fig.11 Dropsonde release events(top view)

进一步对气动力进行量化分析，作不同时刻三个方向的气动力和力矩如图12、图13所示。可见，y方向的气动力很小，其原因是偏航角Ψ较小（如图7所示），并进而使得y方向的速度（图14）及位移均很小。俯仰角Θ较大，因此z方向气动力亦较大。至于x方向的气动力，即气动阻力，明显大于其他两个分量，其值可达重力（G）的5 倍以上，即x方向加速度可超过5g。对于气动力矩而言，由于探空仪呈圆柱体状，因此其轴线方向（即x方向）气动力矩明显小于其他两个方向力矩。

4.3 吊舱尾迹影响

由图12 可见，气动阻力在t=0.06s 之前的值较之后的值偏小，结合图10 所示探空仪位置，可知探空仪在0.06s 之前距离吊舱较近，因此吊舱尾迹可影响探空仪受力。为此作出不同时刻过吊舱轴线的展向截面流场（吊舱尾迹附近，如图15），可见t=0.06s 之前探空仪处于吊舱尾迹区内，而尾迹区流速较低，故探空仪受到的气动力偏小；当时间达到0.1s 后，探空仪已经脱离吊舱尾迹，其受到的来流几乎就是载机飞行来流，故在探空仪姿态变化不大、相对载机运动速度也不太大的时候，气动阻力稳定在较大值附近。

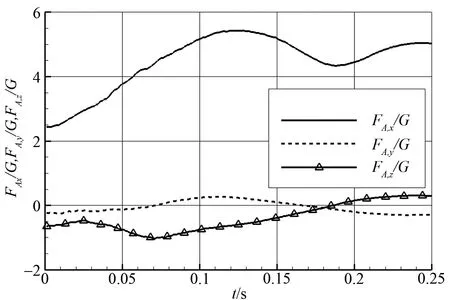
图12 探空仪所受气动力Fig.12 The aerodynamic force of the dropsonde

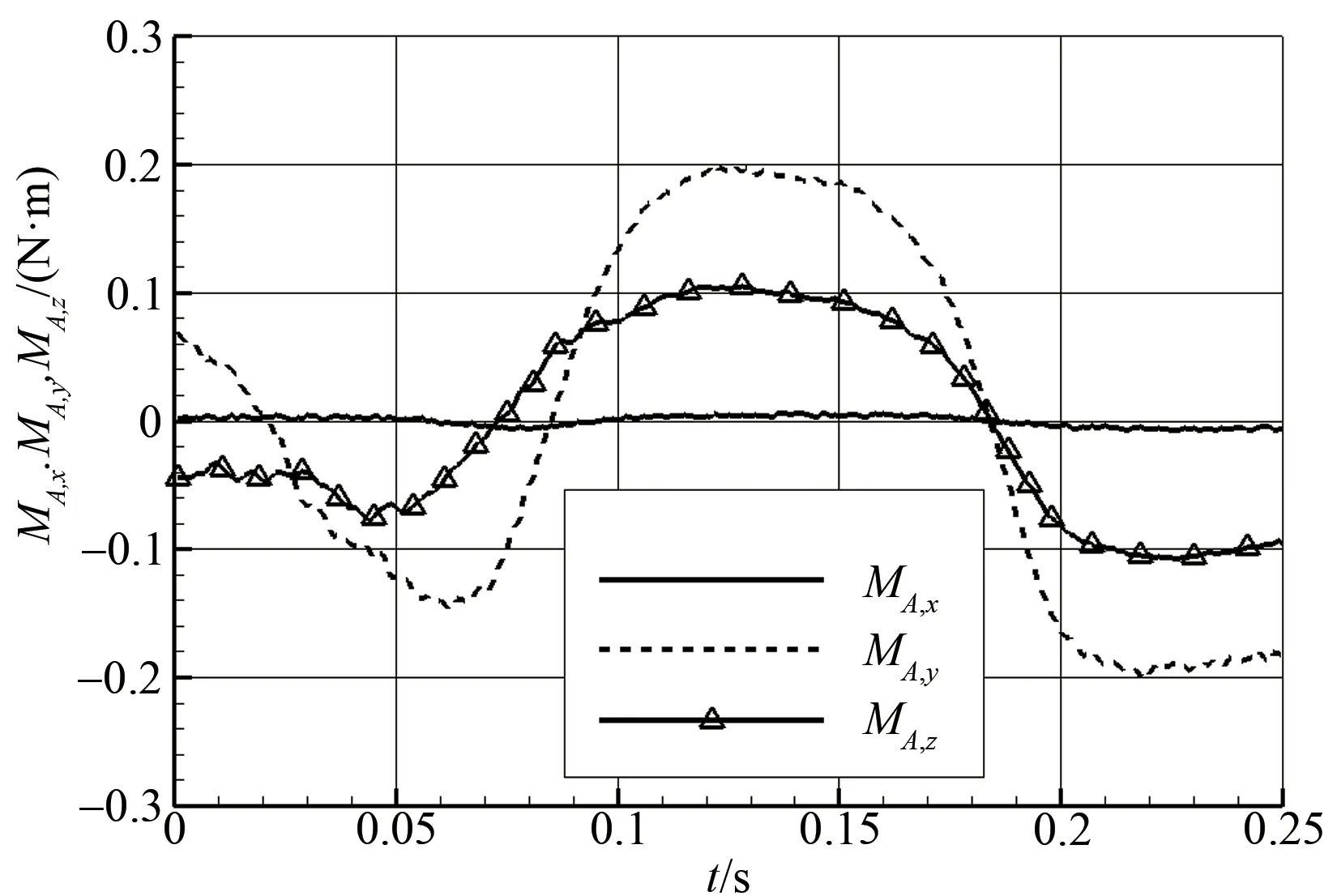
图13 探空仪所受相对质心的气动力矩Fig.13 The aerodynamic moment of the dropsonde

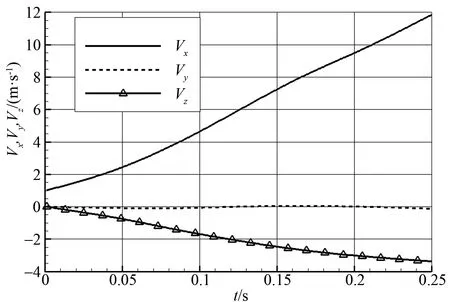
图14 不同时刻探空仪速度Fig.14 The velocity of the dropsonde

4.4 流体粘性的影响

在“弹类”物体的投放过程模拟中，流体域采用欧拉（Euler）方程求解，获得的投放物轨迹及姿态同实验值吻合较好[8-9]。为衡量流体粘性对探空仪轨迹预测的影响，本文还采用Euler 方程来代替RANS 方程求解流体域，模拟探空仪投放过程。Euler 方程本质上是忽略了RANS 方程（1）中的粘性项。同时，壁面边界改为滑移壁面，其他设置保持不变。

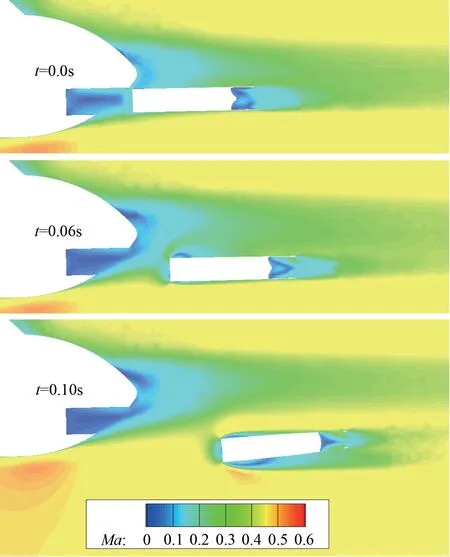
图15 不同时刻吊舱尾迹流场Fig.15 The wake flow of the pod

探空仪轨迹如图16所示，可见欧拉方法获得的轨迹同RANS 方法差别很大，其本质上是由两种方法模拟的流场存在很大差异引起的，如图17 所示，欧拉方法模拟的初始时刻流场同RANS方法模拟的流场存在很大差别。尤其是吊舱尾迹区，RANS 方法模拟的尾迹区较大，而欧拉方法由于没有考虑粘性，其尾迹区范围小得多，因此探空仪所受气动力亦差别很大。

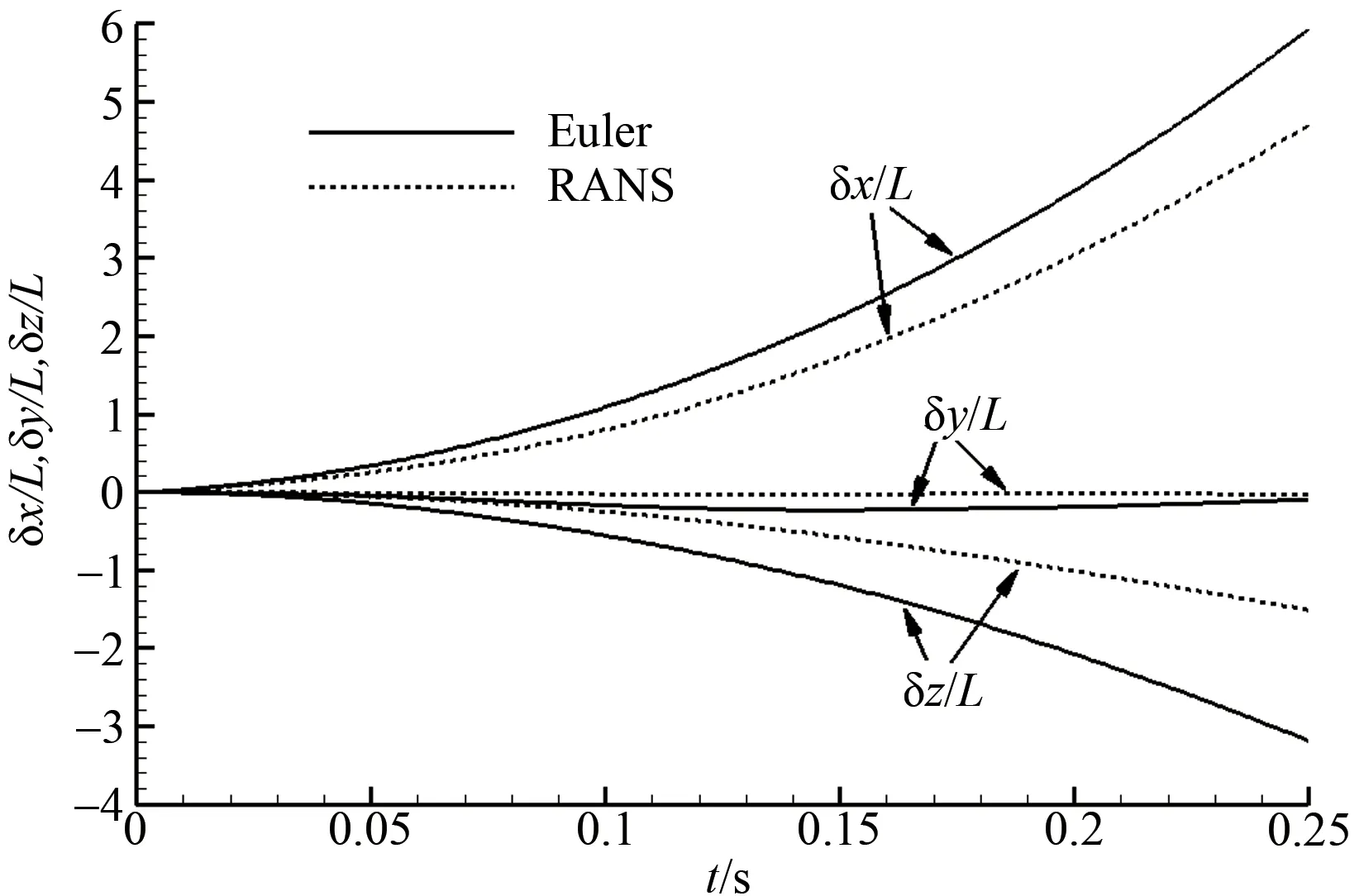
图16 欧拉方法及RANS模拟的探空仪轨迹Fig.16 Dropsonde trajectory of simulations with Euler method and RANS

图17 欧拉方法模拟的吊舱尾迹Fig.17 The pod wake flow of the Euler simulation

5 结 论

本文针对下投探空仪从云影无人机翼下吊舱尾部投放安全性问题，采用非结构动态嵌套网格技术，通过求解RANS方程及六自由度动力-运动学方程，数值模拟了探空仪的投放过程，分析了其运动轨迹、姿态变化及受力情况。作为对比，同时开展了基于欧拉方法的数值模拟。通过研究探索出了适合探空仪投放仿真的数值模拟方法，并得到了下面主要结论：

（1）对于嵌套网格切割问题，一般情况下使用子网格外边界切割背景网格即可；但当子网格同背景网格物面相交时，需要先采用背景网格物面对子网格进行切割。

（2）探空仪的“密度”（重量同其外壳所占流体域体积之比）小，因此投放过程中气动力明显大于重力，流向加速度可达5g以上。

（3）由于探空仪设计有开口端，使其气动力作用点处于重心之后，从而具有一定的稳定性，投放过程中未出现翻滚，姿态角变化范围不大，因此阻力方向气动力明显大于另外两个方向。

（4）相比于吊舱，探空仪尺寸较小，其投放初始段受吊舱尾迹影响很大，气动阻力明显较小。

（5）同“弹类”物体相比，探空仪外形不具有流线型，且开口端流场复杂，如流体域采用Euler 方程模拟，则探空仪投放过程的仪轨迹偏离很大，表明忽略流体粘性不能获得合理的气动力及力矩。在探空仪投放过程的模拟中必须采用RANS，甚至更精确的流动模拟手段。