“一对多”的空间在轨服务序列规划研究

郑红星，周思雨，李伟杰

（1. 哈尔滨工业大学航天学院，哈尔滨150001；2. 北京空间飞行器总体设计部，北京100094）

1 引 言

目前各航天大国纷纷提出以“在轨服务”的方式提高航天器在轨机动能力和工作寿命，升级扩大航天器功能，创造经济效益[1]。美国已经开展了XSS[2]、DART[3]、轨道快车[4]等飞行器试验项目，进行货物运输、模块更换、地面遥操作等技术验证和预先研究[5]。在“在轨服务”任务中，当一颗服务星对多颗在轨运行的目标星进行服务时称为“一对多”服务方式。国外研究表明，“一对多”服务方式优于“一对一”服务方式，并将成为未来在轨服务的主流方式[6]。

国内外已经针对在轨服务的轨道机动方式和自主决策规划等展开了深入的研究。文献[7]针对未来服务型航天器总结了漂移式、组合式、直接弹道式3 种共轨式机动模型，并给出了机动时间、能量、相位的关系式与仿真曲线。文献[8]针对圆轨道航天器在轨燃料加注任务，提出了一种基于聚类分析的在轨加注任务调度及优化算法。文献[9]对运行在地球同步轨道上且倾角较小的卫星群的“一对多”在轨加注任务开展了相关研究，文中将共面转移与变轨道面机动所消耗的燃料进行了比较，并在小角度近似下将该任务规划问题简化成旅行商（TSP）问题进行求解。文献[10]针对在轨服务任务规划问题，建立了一套系统的建模与优化方法，深入研究了在轨服务任务规划模型建模方法。尤其针对在轨加注任务，提出了一套可应用于P2P、“一对多”和混合模式的在轨加注任务规划问题中的系统建模与优化方法。许多文献均将研究重点放在对地球静止轨道（GEO）卫星的服务上，这是由于GEO 轨道高度较高，发射卫星的代价较大，如果能够利用发射到低轨的服务星为其提供在轨服务，延长其寿命，将更有利于减小成本[11]。

本文也将重点研究针对GEO轨道上“一对多”的在轨服务任务，分别考虑服务星与工作星轨道共面与异面情况，服务星的轨道机动采用脉冲变轨的方式，重点通过求解Lambert 问题得到有限转移时间约束下的机动速度增量，以此作为优化指标与遗传算法序列规划相结合，得出使得总脉冲速度增量最小的服务策略。

2 数学模型

2.1 轨道转移任务

为了简化问题我们忽略摄动等因素的影响，将轨道转移简化成只考虑地球一个中心天体的二体问题。一个服务星可以为同一轨道上的多颗工作星提供服务，即“一对多”。首先介绍三种轨道转移的方式。

2.1.1 霍曼转移

在同一轨道平面内，两不相交圆轨道之间的过渡霍曼转移为能量最省的方式。霍曼过渡轨道是一条外切于小圆轨道，内切于大圆轨道的椭圆轨道，由两次脉冲机动实现[1]。

两次机动的脉冲大小分别为：

2.1.2 异面圆轨道转移

对于没有时间约束的两个轨道半径不同的异面圆轨道之间的转移，本文采用了先在初始轨道平面内进行霍曼转移将轨道转移到与新轨道半径相同的异面轨道上，这里进行两次机动。然后在两个异面轨道的交点再施加一次脉冲，用于改变轨道平面，完成转移。

相交的同轨道半径异面轨道机动速度：

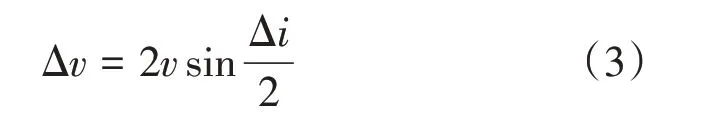
2.1.3 Lambert转移

Lambert 问题是航天动力学中的两点边界值问题，主要研究如何根据两个位置矢量和转移时间确定航天器转移轨道[1]。根据初始时刻服务星的轨道六根数可以得到其位置和速度(r10、v10)，工作星的轨道六根数可以得到同一时刻工作星的(r20、v20)。给定转移时间t，迭代求解出工作星在t时刻后的位置速度(r2f、v2f)，经过t时间后服务星也要到达同一位置。已知服务星初始位置、转移时间和最终位置后，就可以采用转化为Lambert 两点边值问题求解出初始速度v1t与最终速度v1f。由此可以得到两次的脉冲速度：Δv1=v1t-v10和Δv2=v2t-v1f。

2.2 任务规划

该服务任务规划可以理解为服务星选择合适的路径来对工作星进行在轨服务，它将每颗工作星服务一次后回到自身轨道，使得任务完成后消耗的总推进剂最少。该问题实际上就是不对称的TSP。从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的回路。由于该问题的可行解是所有顶点的全排列，随着顶点数的增加，会产生组合爆炸，它是一个非确定性多项式完全（Nondeterministic Polynomial Complete，NPC）问题。

3 分析与讨论

3.1 同面轨道服务

考虑一个服务星为三个工作星提供在轨服务，三颗工作星间隔120°均布GEO 轨道平面上。服务星工作在10000km轨道上。如图1分别为工作星轨道与服务星轨道共面和异面两种情况。

图1 同面轨道转移（左）与异面轨道转移（右）Fig.1 Same-plane orbit transfer(left)and different-plane orbit transfer(right)

将发出在轨服务的指令的时刻记为初始时刻，假设此时三颗工作星的轨道六根数分别为：

服务卫星的轨道六根数为：

假设转移时间tf= 7200s。为方便后面的任务，采用整数编码，服务卫星编号0，工作星分别编号1、2、3。

服务星依次轨道转移到第一颗工作星，第二颗工作星再到第三颗工作星，结束服务后再返回原轨道。前几次服务通常由于存在时间限制采用Lambert轨道转移，最后一次返回原轨道不存在时间限制，所以采用霍曼转移即可。仿真结果计算见表1。

MATLAB仿真得到的部分结果如图2。蓝色为工作星运行轨道，绿色为服务星运行轨道，红色虚线为转移轨道。转移初始时刻服务星位置为绿点，工作星初始位置蓝点，转移结束后同时到达红点处。

表1 同面机动速度Table1 Same-face maneuvering speed

3.2 异面轨道服务

异面时的情况如图1右图所示。服务指令发出时刻假设三颗工作星的轨道六根数与3.1 节中相同，服务卫星轨道六根数为：

图2 同面轨道转移仿真结果图Fig.2 Simulation results of same-plane orbit transfer

同样假设服务星依次轨道转移到第一颗工作星，第二颗工作星再到第三颗工作星，结束服务后再返回原轨道。前几次服务采用Lambert 轨道转移，最后一次返回无时间限制，所以采用先霍曼再异面的转移方式。仿真结果计算如表2。

表2 异面机动速度Table2 Different-plane maneuvering speed

图3 异面轨道转移仿真结果图Fig.3 Simulation results of different-plane orbit transfer

3.3 基于遗传算法的规划

根据3.1和3.2 节的分析，已得到同面变轨和异面变轨的模型，并计算得出0 ↔1、0 ↔2、0 ↔3、1 ↔2、2 ↔3、1 ↔3 的机动速度，接下来需要求解使得机动速度总和最小的在轨服务方案。该问题隶属于整数规划问题，解空间为离散变量，模型的梯度等信息不存在。针对此类问题的特点，遗传算法具有较强的优势，它通过模仿物种群中优胜劣汰的选择机制以及种群中优势个体的繁衍进化来实现优化功能[1]，因此本文采用遗传算法求解。算法流程如图4所示。

3.3.1 求解过程

图4 算法流程图Fig.4 Algorithm flowchart

随机产生一个种群作为初始种群，同时计算这个初始种群的适应度——取机动速度总和的倒数作为适应度，适应度越高，被保留概率越大。值得注意的是，由于整个在轨服务的模型需从服务星开始机动，所以种群的首序号不为0时，适应度函数为无穷大。每次完成交叉、变异运算之后也需要重新评价。

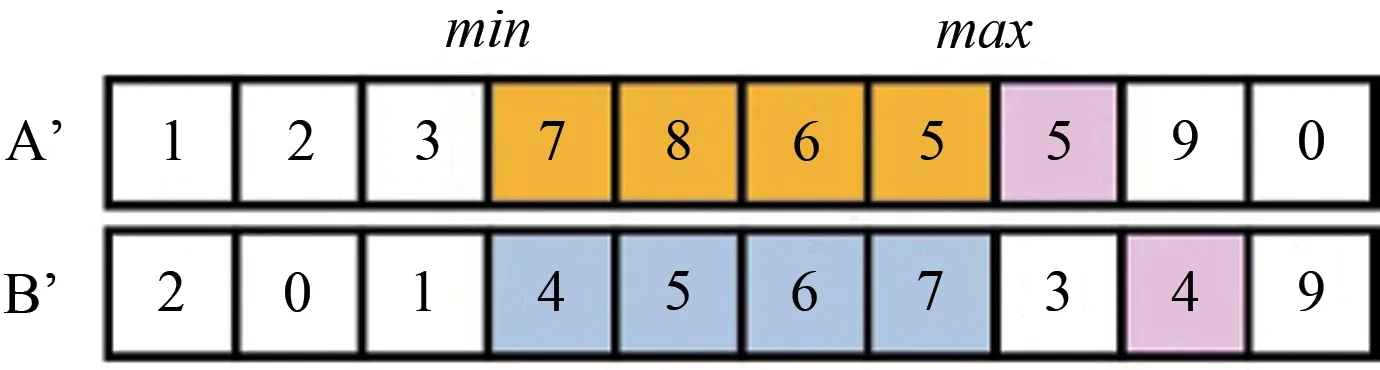
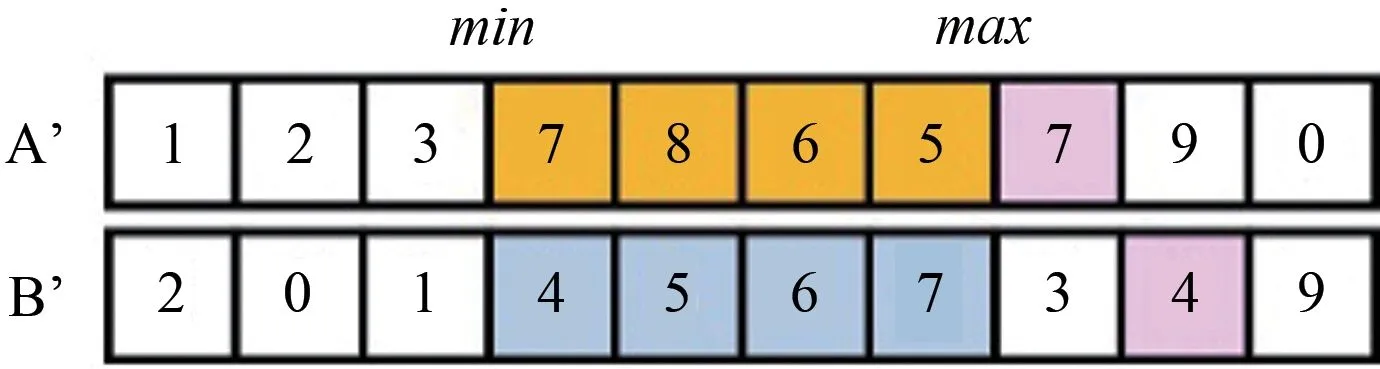
交叉运算操作如图5和图6所示，选择两个个体，在[1，sz]（sz为服务星和工作星的总数量）的范围内，随机产生两个交叉位min和max（min

图5 交叉前示意图Fig.5 Schematic diagram before crossing

图6 交叉后示意图Fig.6 Schematic diagram after crossing

其中，A、B是未发生交叉之前的染色体（个体），A’和B’是A、B 发生交叉之后产生的新个体。通过冲突检测，发现交叉之后会产生同一个基因在同一条染色体上重复出现，此为交叉的冲突，如图6粉色标注部分。对图6消除基因冲突的示意图如图7~10所示。

变异运算操作首先在随机产生两个变异位min、max，其中min

图7 将染色体A冲突基因8改为染色体B对应位置的5Fig.7 Change chromosome A conflict gene 8 to 5 corresponding to chromosome B

图8 将染色体A冲突基因5改为染色体B对应位置的7Fig.8 Change chromosome A conflict gene 5 to 7 corresponding to chromosome B

图9 将染色体A冲突基因7改为染色体B对应位置的4Fig.9 Change chromosome A conflict gene 7 to 4 corresponding to chromosome B

图10 对染色体B同样进行消除冲突Fig.10 Conflict elimination on chromosome B

图11 变异结果Fig.11 Variation results

算法的终止条件是达到最大代数的迭代次数，每一次迭代结束后将得到的路径长度和当前代数（第几代）记录在数组中，然后在搜索完成之后，将数组中记录的最短路径和对应的代数输出，作为搜索结果。

3.3.2 结果分析

求解TSP 的遗传算法是利用MATLAB 软件编程的。由于遗传算法包含了随机搜索方法，所求的最优解不一定是实际最优的。在求解过程中，发现遗传算法得到的结果的精确度除了和交叉算子、变异算子、适应度计算方法有关，还受交叉概率、变异概率、迭代次数的影响。对于本文算法，在一定范围内，迭代次数也大，变异概率越小，遗传算法的精确度越高；执行时间随着迭代次数的增加而增加。当交叉概率为0.8，变异概率为0.5，最大代数为10000 时，能得到较理想的结果，如图12所示。

图12 搜索过程图Fig.12 Search process diagram

遗传算法得到的最小机动速度总和为44.00km/s，最短路线为0 →1 →2 →3 →0。

4 结 论

本文忽略轨道摄动等影响因素简化轨道转移问题，对“一对多”模式的在轨服务任务规划问题进行了研究。分别考虑了服务星与工作星轨道共面与异面的情况，假设轨道机动采用脉冲变轨的方式，针对不同的约束条件通过求解Lambert 问题、霍曼转移或异面圆轨道转移得到相应的机动速度增量，并将总机动速度增量作为优化指标，采用遗传算法序列规划得出使得总脉冲速度增量最小的服务策略。