5阶完美幻方一览表

张在明1,刘兰芝

(1.玉溪师范学院，云南 玉溪 653100;2.玉溪市教科所，云南 玉溪 653100)

本表(初稿)是在刘辑熙老先生编著《五阶幻方追踪》书内第二章七十二对孪生姐妹(也就是5阶完美幻方总表——笔者注)的基础上制作的.本表分成两大类：I为周期5×5，共120个完美幻方，又分成各自独立的20个为一组，共20×6=120，II为周期5，也有6组，每组含4个完美幻方，共4×6=24，所以总共为20×6+4×6=144，恰好为5阶完美幻方的全部.

本表所用的方法为两种置换(substitution):其一为数字置换

在表中记为+5，由上而下标示出;

其二为康威置换(Conway substitution),简记为CS，表中由左向右标示出，所谓CS置换，乃由康威菱形法制作幻方而来，乃位置置换，列表如下：

11213141514352112534122232425254132231451323334353CS15243342511424344454➝213544531215253545553241551423

其对完美幻方的探索很有用.事实上，容易看出,康威置换的作用就是把行、列变成泛对角钱，同时把原来的泛对角线变成行、列.再说具体一点，是把行变成左泛对角线，把列变成右泛角线，而原幻方中的泛左(右)对角线则相应变成新幻方中的列(行).借用金庸武侠小说中的词语,康成置换就是“乾坤大挪移”.

顺便说两句：I类每组20个幻方，经+5和CS置换可以组成很多闭合系统，而II类每个幻方经+5置换后均原样不变，它们这些特点，恐可用群论理论探究.

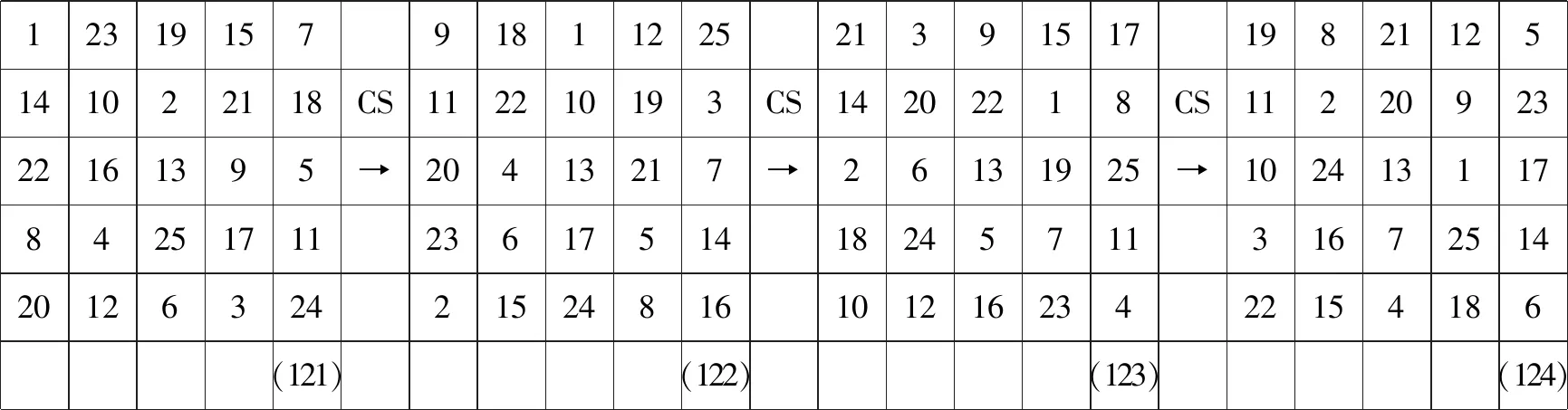
I周期5×5

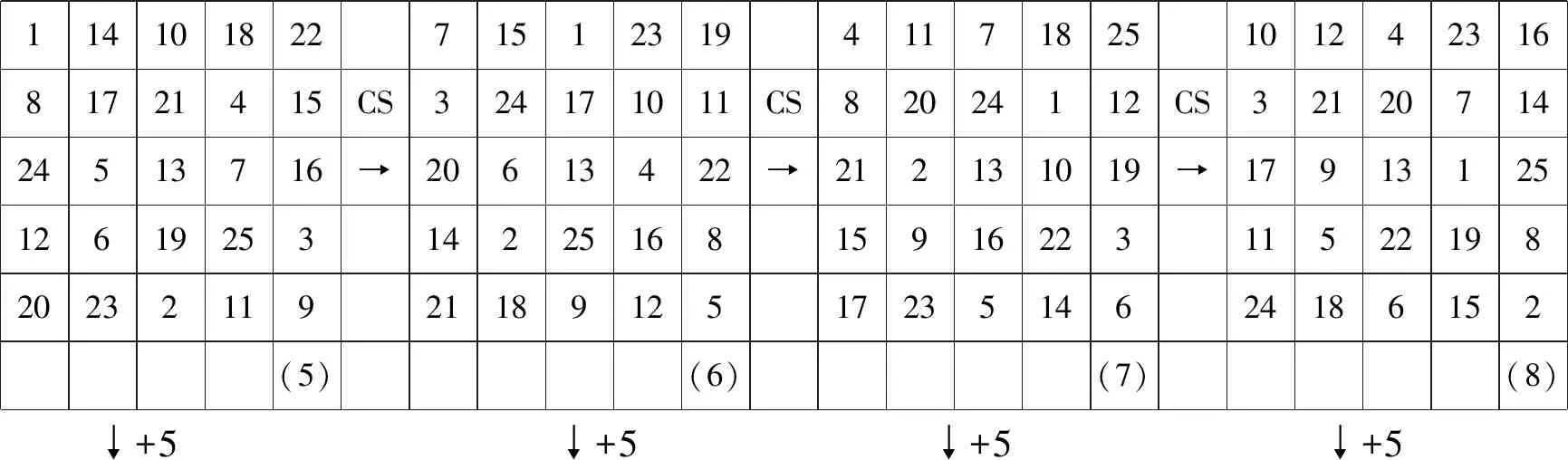
114101822715123194117182510124231681721415CS324171011CS82024112CS3212071424513716➝20613422➝212131019➝179131251261925314225168159162231152219820232119211891251723514624186152(5)(6)(7)(8) +5 +5 +5 +5

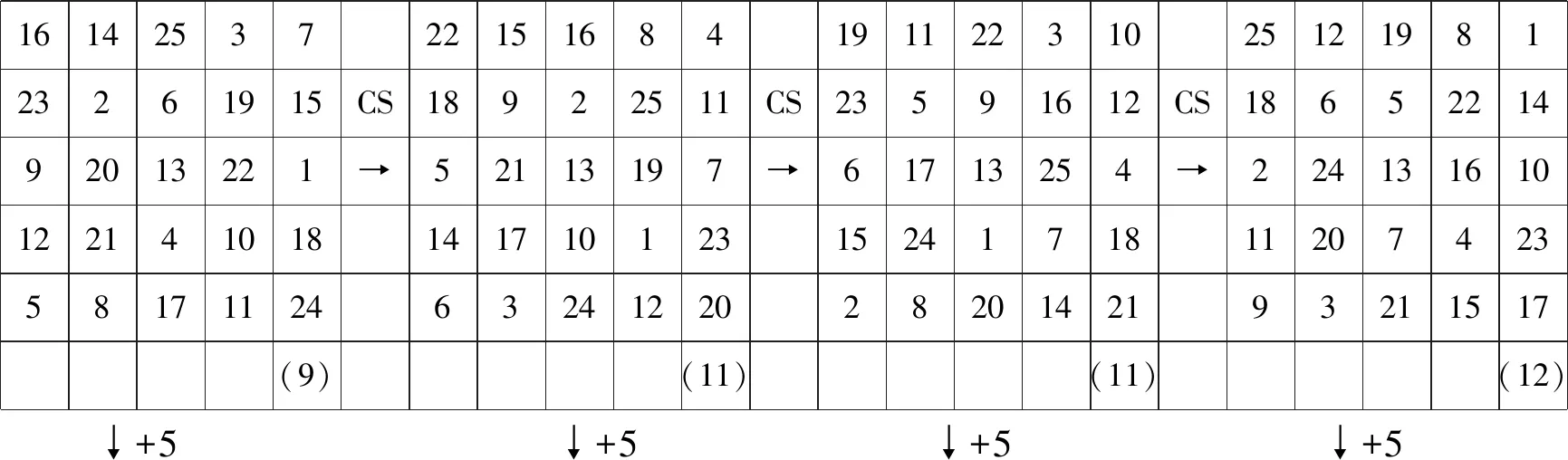
16142537221516841911223102512198123261915CS18922511CS23591612CS1865221492013221➝52113197➝61713254➝224131610122141018141710123152417181120742358171124632412202820142193211517(9)(11)(11)(12) +5 +5 +5 +5

6142518222156319911221852512931623171915CS84172511CS23204612CS81202214410132216➝20211392➝17132519➝172413651221195814751623152416281110219232037112411824121017310142141821157(13)(14)(15)(16) +5 +5 +5 +5

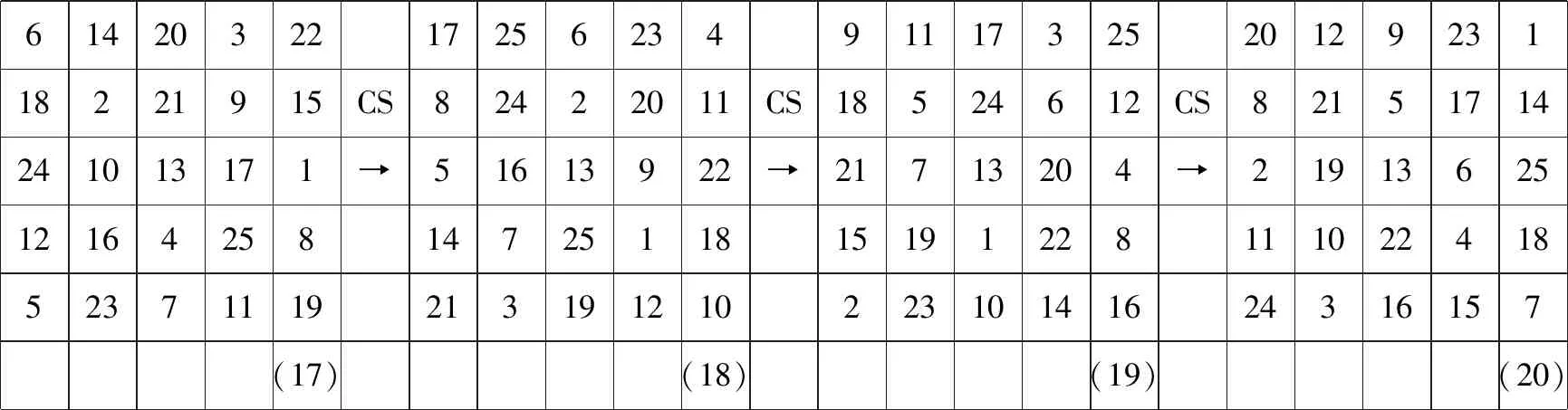
6142032217256234911173252012923118221915CS82422011CS18524612CS82151714241013171➝51613922➝21713204➝219136251216425814725118151912281110224185237111921319121022310141624316157(17)(18)(19)(20)

11824157923112201639152224816125141021623CS111710243CS14251718CS1122591817211395➝25413167➝26132420➝10191312284202211186225142319571132172014251263192151982110122118417154236(21)(22)(23)(24) +5 +5 +5 +5

21319157918211251239151719811225141022118CS112101923CS14202218CS1122209321613925➝20241317➝22613195➝10413211782451711361725141842571123167514201262342215481610121632421524186(25)(26)(27)(28) +5 +5 +5 +5

62319152418612252184151719321121014572118CS11225198CS14202263CS11720423221613410➝20913212➝71131925➝52413617392517112311710141824102118162251420121824715243165121623922159181(29)(30)(31)(32) +5 +5 +5 +5

2118915248211220162341579316122514522168CS11175923CS141017213CS11221041817613425➝102413162➝22113920➝5191321732420711181725148192521123622014101212319221519365126182417152481(33)(34)(35)(36) +5 +5 +5 +5

63241517192361251819152224181121014207123CS11220248CS14252618CS11725193221131910➝25913117➝71613245➝20413622189522113162210142341017118211751425121684715418212012213921592316(37)(38)(39)(40)

1151923717141825511172391912582118226514CS310221911CS182410112CS36241715104131721➝24161357➝62131925➝2220131912162593152921181420217311472518248211206232012422841516102316142(41)(42)(43)(44) +5 +5 +5 +5

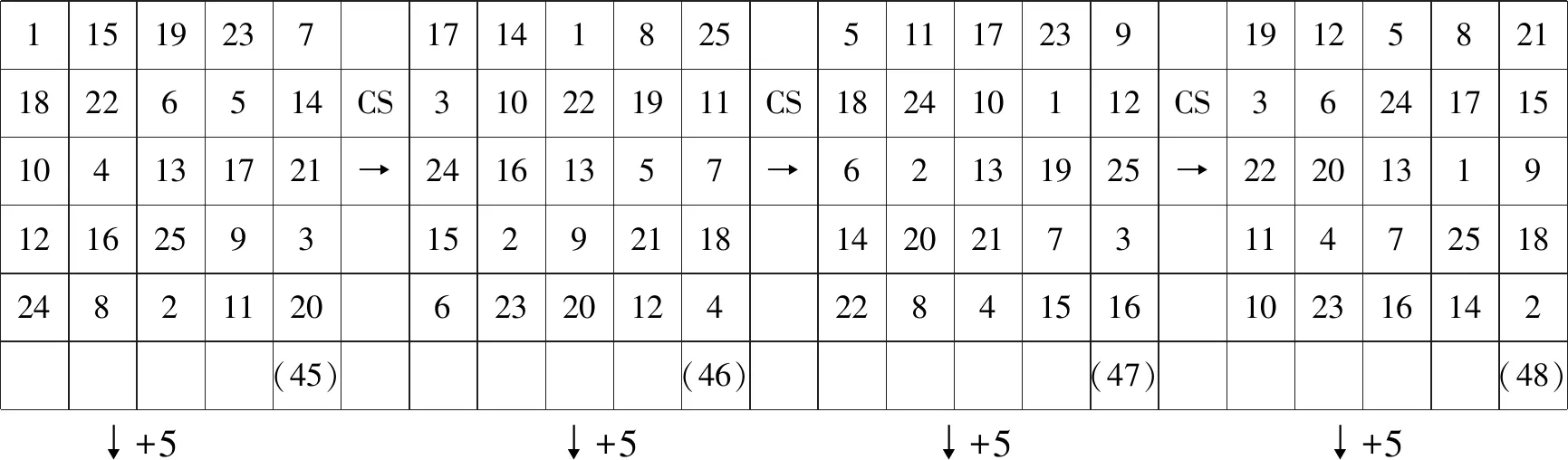
1151923717141825511172391912582118226514CS310221911CS182410112CS36241715104131721➝24161357➝62131925➝2220131912162593152921181420217311472518248211206232012422841516102316142(45)(46)(47)(48) +5 +5 +5 +5

1615243722141685201122392412208123262014181022411CS234101612CS18642215101913221➝42113207➝61713245➝2251316912215918151791231425171811197523481711256325121928191521103211417(49)(50)(51)(52) +5 +5 +5 +5

6152418222146320101122184241210316231711014CS85172411CS23195612CS8119221559132216➝192113102➝17132420➝172513641221204815741623142516281192202319371125118251291739152151821147(53)(54)(55)(56) +5 +5 +5 +5

6151932217146235101117324191210231182211014CS82521911CS18425612CS8214171525913171➝416131022➝21713195➝220136241216524815724118142012281192251842371120213201292239151625316147对称(57)对称(58)对称(59)对称(60)

118251471023112191631014222581612415921623CS11179253CS15241718CS112241018172113104➝24513167➝26132519➝920131228519221118622415232047113217191524126320214208219122118517145236(61)(62)(63)(64) +5 +5 +5 +5

213201471018211241231014172081122415922118CS11292023CS15192218CS112219103216131024➝19251317➝22613204➝951321178254171136172415185247112316741519126235221458169121632521425186对称(65)对称(66)对称(67)对称(68) +5 +5 +5 +5

623201425186122421851417203211291547211811224208CS15192263CS1171952322161359➝191013212➝711132024➝425136173102417112311791518259211816224151912182571425316412162310221410181(69)(70)(71)(72) +5 +5 +5 +5

211810142582112191623514710316122415422168CS111741023CS15917213CS1122951817613524➝92513162➝221131019➝420132173251971118172415820242112362191591212320221420364126182517142581(73)(74)(75)(76) +5 +5 +5 +5

6325141720236124182014222518112915197123CS11219258CS15242618CS1172420322113209➝241013117➝71613254➝195136221810422113162291523591711821174152412168571451821191221310214102316(77)(78)(79)(80)

11220239191518222111923102014282118246215CS37242011CS18257114CS3625191275131921➝25161329➝64132022➝241713110141622103124102118151721931159221825841117623171452485121672316154(81)(82)(83)(84) +5 +5 +5 +5

112101824915123172119182510142231681921215CS322191011CS82022114CS3212091222513916➝20613224➝214131017➝197131251461725312425168157162431152417820234117211871451923512622186154(85)(86)(87)(88) +5 +5 +5 +5

1612253924151682171124310251417812346171518742511CS23571614CS1865241272013241➝52113179➝61913252➝422131610142121018121910123152219181120922358191122632214204820122173211519(89)(90)(91)(92) +5 +5 +5 +5

6122518424156317711241852514731623191715CS82192511CS23202614CS81202412210132416➝20211374➝19132517➝192213651421175812951623152216481110417232039112211822141019310122121821159(93)(94)(95)(96) +5 +5 +5 +5

6122032419156232711193252014723118421715CS82242011CS18522614CS82151912221013191➝51613724➝21913202➝417136251416225812925118151712481110242185239111721317141042310121622316159(97)(98)(99)(100)

11822159723114201637152422816145121041623CS111910223CS12251918CS1142571819211375➝25213169➝46132220➝10171312482202411186245122317591132192012251463174151782110142118219152236(101)(102)(103)(104) +5 +5 +5 +5

21317159718211451237151917811425121024118CS114101723CS12204218CS1124207341613725➝20221319➝24613175➝10213211982251911361925121822591123169512201462322415281610141632241522186(105)(106)(107)(108) +5 +5 +5 +5

6231715421861425218215191732114101259211811245178CS12202463CS11920223241613210➝20713214➝91131725➝52213619372519112311910121822104118164251220141822915223165141623724157181(109)(110)(111)(112) +5 +5 +5 +5

2118715428211420162321597316142512524168CS11195723CS121019213CS11241021819613225➝102213164➝24113720➝5171321932220911181925128172541123642012101412317241517365146182219152281(113)(114)(115)(116) +5 +5 +5 +5

63221519172361451817152422181141012209123CS11420228CS12254618CS11925173421131710➝25713119➝91613225➝20213624187524113162410122321019118211951225141682915218212014213741572316(117)(118)(119)(120)

II周期5

123201471018112242131014172082112415922118CS11229203CS15192218CS112191023221613104➝19513217➝26132024➝925131178524171123617415182547113167241519126325214258169121623522145186对称(125)对称(126)对称(127)对称(128)

12317159718114252137151917821145121042118CS112410173CS12202418CS1142072324161375➝20213219➝46131725➝10221311982251911236195121822591131692512201463224152281610141623224152186(129)(130)(131)(132)

123201291018114222131012192082114215742118CS11247203CS15172418CS114171023241613102➝17513219➝46132022➝725131198522191123619215182529113169221517146325412258167141623524125186对称(133)对称(134)对称(135)对称(136)

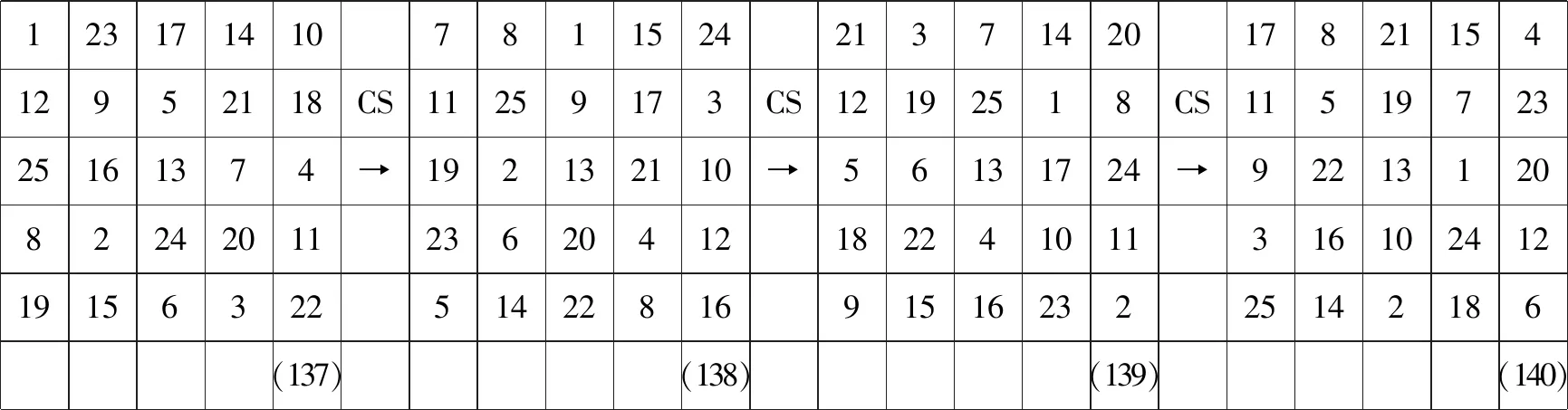
1231714107811524213714201782115412952118CS11259173CS12192518CS1151972325161374➝192132110➝56131724➝92213120822420112362041218224101131610241219156322514228169151623225142186(137)(138)(139)(140)

12319121091811522213912201982115214752118CS11257193CS14172518CS1151792325161392➝174132110➝56131922➝72413120842220112362021418242101131610221417156324512248167151623425124186(141)(142)(143)(144)

值得交待的是，本文利用两个置换来对完美幻方进行分类的方法，同样适用于所有的质数阶完美幻方.例如7阶完美幻方，两个置换为+7与CS，也分成两大类：一类是周期7×7，每组有7×6=42个完美幻方;一类是周期7，每组有6个完美幻方.对此,笔者已有初步的结果.遗憾的是,笔者毕竟势单力薄，加之不会设计算法，所以目前的一点成果都是手算取得,极大地影响了结果的及时呈现.