能源消费量与GDP的统计分析及预测

(玉溪师范学院 数学与信息技术学院，云南 玉溪 653100)

考察能源消费量与经济增长及发展趋势，进行经济统计研究和预测分析，可以反映经济发展与能源发展的趋势，为相关部门提供更好的科学决策依据.目前，常用的预测方法有定性预测法、回归预测法和时间序列法.其中，定性预测是以主观逻辑判断为主的预测方法；回归预测是以变量为基础研究多个变量之间是否存在某一特定关系，是用一个或多个变量的值来预测因变量的值；时间序列预测是用过去时间序列进行统计分析来预测未来时间序列.

预测GDP的常用方法有时间序列预测、神经网络预测、灰色预测及各种组合模型.例如，王冬冬[1]利用1997年到2014年重庆市GDP数据基于ARIMA和BP神经网络模型对重庆市2015年到2017年GDP做出预测，预测精度为97.01%，得到该模型具有较好的拟合效果.孙皖宇[2]分析2000年到2016年中国GDP季度数据并基于季节SARIMA模型对中国2017年各季度数据进行预测，得到GDP平均误差为4.478 7%；未来我国GDP将持续增长，但增长率逐渐减少；且固定在7%左右，最为适合中国经济发展.王红超、王红蕾[3]利用我国2006年到2015年GDP数据采用二次指数平滑法与回归分析相结合的方法，对我国2017年GDP进行预测.李佩、彭斯俊[4]为了提高组合预测的精度，提出了一种新的组合权重计算方法，该方法通过将平均绝对百分数误差(MAPE)和最小二乘法相结合来确定组合预测模型的权重值，并对湖北省GDP进行预测，预测结果表明该组合权重与单一权重相比，可将组合模型的预测精度提高约0.3%.李小月[5]利用1990～2010年中国GDP数据，在建立ARIMA、多项式趋势拟合模型和GM(1，1)模型基础上，以误差平方和最小为最优准则建立组合预测模型，并把它应用于我国GDP的预测，所得结果误差优于三个模型的分别预测，表明组合预测模型在时间序列数据的预测中更有优势.然而，对于GDP预测，由于选取的地点、时间、预测分析方法不同，预测结果也多种多样.相对而言，组合模型把各个独立模型的优势进行整合，把信息利用率最大化，可以避免有效信息的浪费也能减少偶然因素对预测结果的影响，其预测精度相对较高[6,7]，因此，组合模型在能源、GDP等预测中得到了广泛应用.例如，周扬等人建立BP神经网络与灰色GM的优化组合模型对江苏省未来15年煤炭和石油的需求量进行预测[6].王莎莎等人采用组合模型预测了中国GDP的发展情况[7].

当前，云南省大力培育和发展烟草、生物资源、旅游、矿产、电力五大支柱产业群[8～12]，五大支柱产业群已经在云南省GDP中占有了较大份额，成为了云南省经济增长的重要保障.如何研究云南省经济增长情况及发展趋势成为目前亟待解决的热点问题.基于上述考虑，本文选取云南省能源消费量占比较大的煤炭、石油、一次电消费量的统计数据，采用组合模型，即多元线性回归与时间序列ARIMA预测模型来研究能源消费量与云南省GDP的关系，并对未来几年云南省GDP进行分析及预测.

1 模型原理介绍

1.1 多元线性回归模型

在处理实际问题时，影响一个变量Y的因素通常是有多个.如果有p个自变量，自变量为xi(i=1,…,p)与随机变量Y之间存在相关关系，通常就意味着xi变量取定值后，Y便有相应的值与之对应.线性回归模型可以表示为：

Y=β0+β1x1+β2x2+…+βpxp+ε

(1)

其中,β0是常数项，ε是随机误差表示由于客观原因没有考虑到的其他因素，β1、β2…βp是回归系数.为了让建立的模型能达到预期效果，必须保证选择的自变量对因变量有显著的影响，并且具有密切的相关性，同时自变量之间要有互斥性，自变量的统计数据也要完整.在得到多元线性回归方程之后，需要对模型进行检验，即要测定模型的拟合度，通过对回归方程、回归系数的显著性检验，判别多重共线性，才能得到拟合度较好的线性回归模型.

1.2 时间序列预测模型

时间序列是指一个依时间顺序做成的观察资料的集合.时间序列分析过程中最常用的方法是：指数平滑、自回归、综合移动平均及季节分解.本次实验研究云南省GDP与能源消费量的关系，但能源消费量往往受到许多因素的制约，这些因素之间有着错综复杂的联系，因此，运用结构性的因果模型分析和预测能源消费量往往是比较困难的.

该预测模型对数据处理需要特别注意三点：一是对有缺失值的数据进行修补；二是将数据资料定义为相应的时间序列；三是对时间序列数据的平稳性进行计算观察.根据时间序列的特征和分析的要求，选择恰当的模型进行数据建模和分析，则需要预测年限的数据即可得到.

2 数据分析

2.1 能源消费量组成分析

为研究云南省GDP值的变化与能源消费量的变化关系，根据1978年至2017年能源消费量数据统计，发现云南省能源消费量中煤炭、石油、一次电、天然气消费量占比较大，其中煤炭、石油、一次电消费量又相对较大，所以本文研究云南省GDP与煤炭、石油、一次电消费量的关系.

2.2 能源消费量组成分析

分析1978年以来云南省地区GDP-y，选取煤炭消费量—x1、石油消费量—x2、一次电消费量—x3、能源消费总量—x4为自变量，数据如表1.

表1 云南省1978年～2017年GDP与能源消费量统计

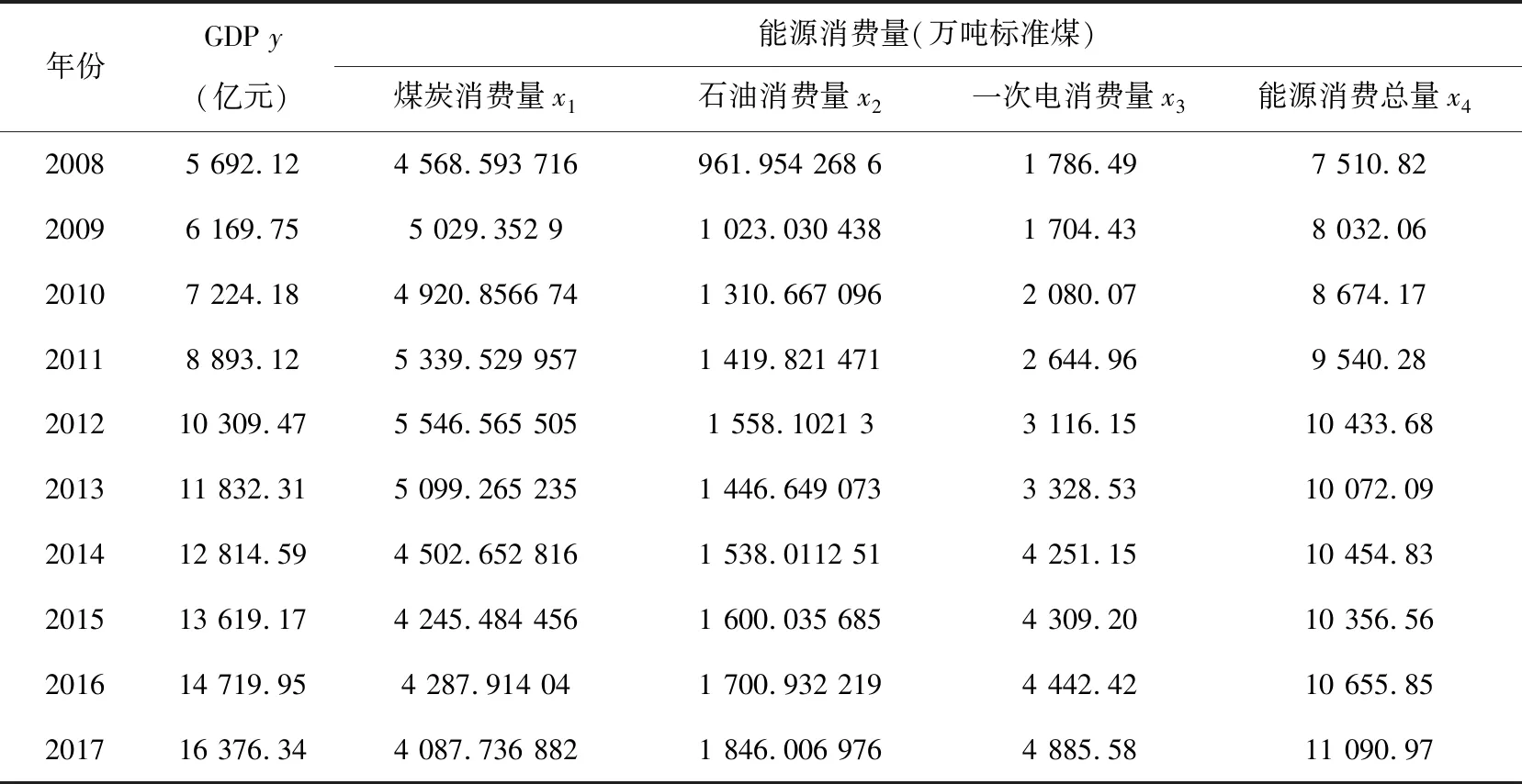
续表1

数据来源：2018年《云南省统计年鉴》.

3 数据处理及模型建立

根据表1数据，利用SPSS可画出散点图1：根据散点图分布情况可以发现云南省煤炭消费量和GDP无线性关系，石油消费量和一次电消费量与GDP成线性关系，所以选择线性模型进行建模.

3.1 数据处理

根据上述散点图分析可将1978年至2015年数据导入SPSS软件，点击变量视图更改标签→分析→回归→线性，煤炭消费量、石油消费量、一次电消费量为自变量，GDP为因变量，置信区间为95%水平，选择逐步回归分析法进行数据分析研究.

图1 煤炭消费量、石油消费量以及一次电消费量与生产总值的关系图

表2 模型参数及检验说明

表2中，a为预测变量(常量)，一次电消费量;b为预测变量(常量)，一次电消费量，石油消费量.模型1自变量为一次电消费量，模型2自变量为一次电消费量、石油消费量，因变量都为GDP，剔除了自变量煤炭消费量，符合散点图预分析.根据R2可以判断线性方程的拟合度，越接近1，说明方程的拟合度越好.模型2调整后R2为0.995，比模型1调整后R2(0.987)更接近1，且都在0.96以上，表明模型2的拟合度是最好的.

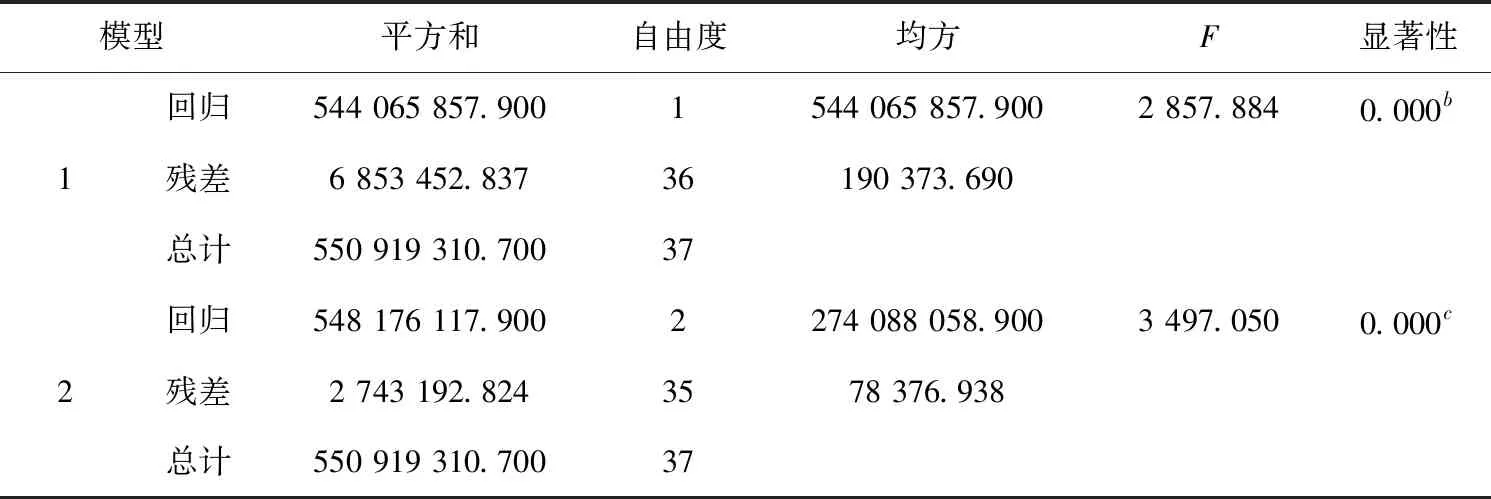
表3 模型显著性检验

说明:a.因变量：GDP;b.预测变量(常量)，一次电消费量;c.预测变量(常量)，一次电消费量，石油消费量.

表3是方差分析数据，F值是对整个回归方程的显著性检验，当F对应的显著性值小于0.05时，回归方程才有意义.从表中可以可看出两个模型的F值对应的显著性值都小于0.05，说明各模型自变量综合起来看对因变量是有显著性影响的，模型可以使用.

表4 回归系数及显著性检验

说明:a.因变量：GDP.

表4给出了线性方程的回归系数及显著性检验，这里的t检验是对单个变量的显著性检验，当t对应的显著性值小于0.05时，回归方程才有意义.从表中可以看出t对应的显著性值都为0，所以各个自变量单独来看对因变量是有显著影响的.B表示各个自变量在方程中的系数.各自变量的B的95.0%置信区间都在10以下，说明各自变量并无较强的多重共线性.

3.2 模型建立

根据分析结果，石油消费量、一次电消费量对GDP的影响是显著的，并且各个变量之间也不存在较强的多重共线性，说明数据分析结果是有效的，建立的模型也是有意义的.相比较而言，模型2的拟合度更好，自变量显著性更高.所以将表4中模型2的各自变量回归系数代入线性回归模型，得到回归方程：

y=-651.407+2.248x2+2.454x3

(2)

3.3 模型检验

将2016年、2017年石油和一次电消费量代入(2)式，检测模型得到GDP值与实际值的对比如表5所示，可以看出误差率在6.00%以下，在可接受范围内.

表5 模型计算值与实际GDP值对比

再加入2016年和2017年数据，并用以上相同的方法、步骤修正模型，可以得到修正模型：

y=-689.896+1.95x2+2.650x3

(3)

如图2，将修正模型(3)式得到的GDP和实际GDP建立折线统计图，拟合效果比较理想.

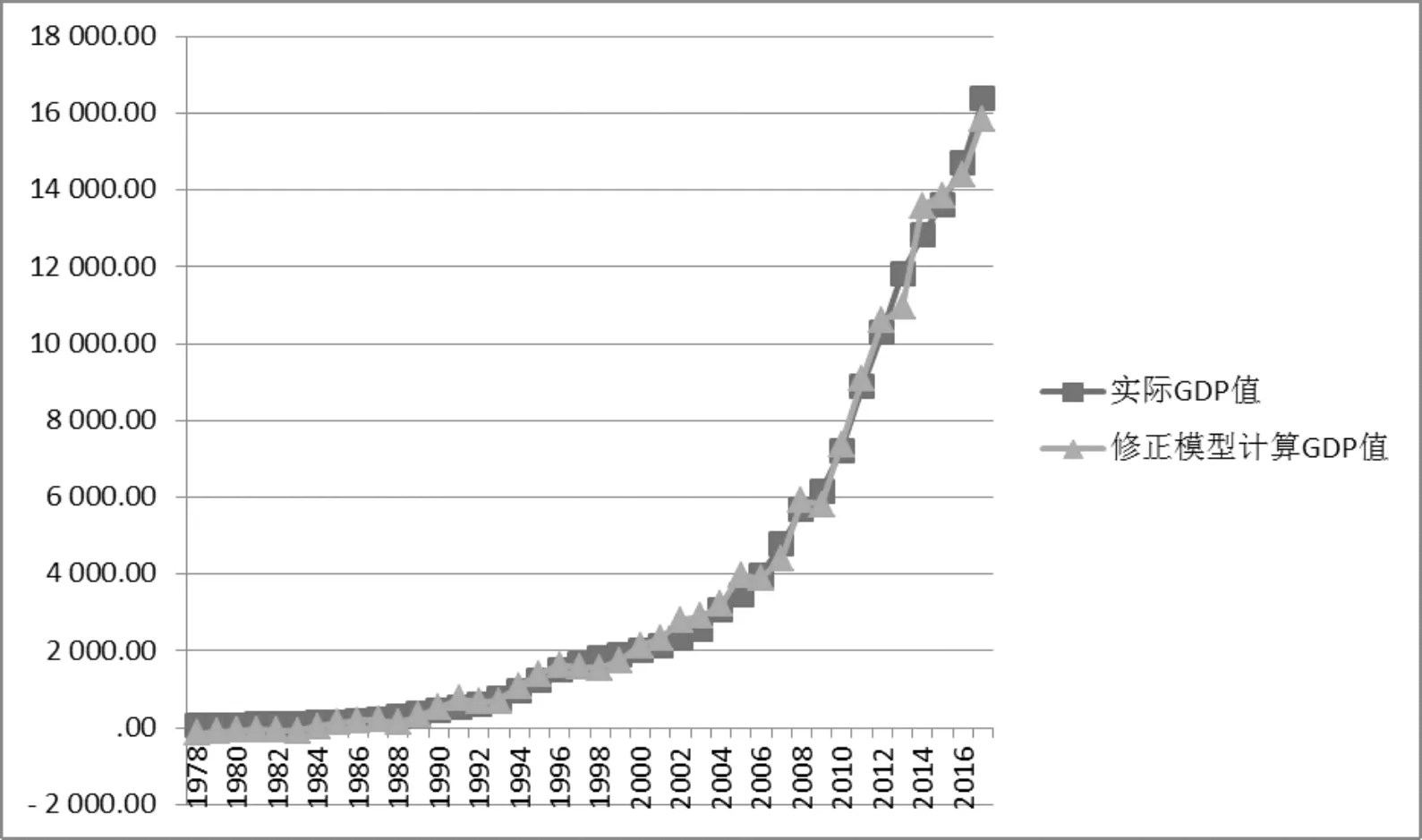
图2 修正模型计算GDP值与实际GDP值拟合度

4 石油、一次电消费量预测模型

从上述分析中可得到云南省GDP预测模型为(3)式：

y=-689.896+1.95x2+2.650x3

为了应用模型(3)式预测2018～2022年云南省GDP,还需预测2018～2022年的石油消费量、一次电消费量.下面利用时间序列ARIMA预测模型研究石油消费量、一次电消费量的预测模型.

4.1 石油消费量预测模型

根据自相关和偏相关图判断该数据是平稳的，对原始序列建立(p,0,q)模型，经过反复试验确定模型为ARIMA(5，0，5)，此时R2达到0.990，拟合程度较好．

石油消费量预测通过以上分析采用ARIMA(5，0，5)模型建模，得到以下预测值．

表6 石油消费量预测值

表6中，对于每个模型，预测从所请求估算期范围内的最后一个非缺失值之后开始，并结束于最后一个所有预测变量都有可用的非缺失值的周期，或者在所请求预测期的结束日期结束，以较早者为准.

从图3中的拟合度对比图可看出，该预测模型拟合度较好，可清晰看出石油消费量预测趋势.

图3 石油消费量预测拟合度对比图

4.2 一次电消费量预测模型

数据处理和石油消费量预测一样，同样将原始数据1978～2017年数据导入SPSS，通过同样的方法可得到预测值.

根据自相关和偏相关图判断该数据是非平稳的，进行了一次差分，得到差分序列自相关和偏相关图都是拖尾的，因此可对原始序列建立(p,1,q)模型，经过反复试验确定模型为ARIMA(5，1，6)，此时R2达到0.992，拟合效果较好．

一次电消费量预测通过以上分析采用ARIMA(5，1，6)模型建模，得到以下预测值．

表7 一次电消费量预测值

表7中，对于每个模型，预测从所请求估算期范围内的最后一个非缺失值之后开始，并结束于最后一个所有预测变量都有可用的非缺失值的周期，或者在所请求预测期的结束日期结束，以较早者为准.

图4中拟合度对比图可看出该预测模型拟合度较好，可清晰看出一次电消费量预测趋势.

图4 一次电消费量预测拟合度对比图

5 结 论

GDP预测结果及分析分别把表6和表7中的2018～2022年石油消费量和一次电消费量带入修正模型

y=-689.896+1.95x2+2.650x3，

(3)

得到2018年～2022年云南省地区GDP预测数据如下：

表8 修正模型GDP 预测值

(1)云南省未来石油消费量和一次电消费量依然处于上升水平，虽然有时会有波动，但总体波动不大.

(2)云南省一次电消费量还处于急速增长状态，未来一次电消费量应会持续增加.

(3)云南省GDP值处于上升水平，但是增速相对缓慢.

(4)从本文的预测数据看，2019年GDP相对2018年GDP出现稍微下降趋势，这为云南省制定下一步相应政策提供了一定的数据依据.需要说明的是，由于2019年出版的是2018年的统计年鉴，而在本文成文时年鉴中的数据只更新到2017年，从时效看稍显滞后，但新出来的数据也能对本文预测结果做一个及时的验证.

模型说明

(1)本文采用SPSS多元线性回归模型和时间序列ARIMA预测模型组合来预测未来5年云南GDP值，具有较高的精确性和可靠性，为云南省制定相应政策提供数据支持.

(2)ARIMA预测模型既能提取序列的确定性信息，又能提取其随机性信息，提高了模型的拟合精度，具有确定性分析和随机性分析的优点.

(3)ARIMA预测模型，随着预测时间的延长，预测误差会逐渐增大，精度也会随之下降，进而影响组合模型的精度.

(4)ARIMA预测模型具有较强的时间趋势.