基于DTCWT与LSSVM的风电场短期风速预测

李辉，陶伟，姜一波，李大锦，王林昌，吴杰

(常州工学院电气信息工程学院，江苏常州213032)

近年来风力发电机组单机容量和大型并网风电场的发电总容量迅速增长，由于技术的不断成熟，其发电成本已接近常规能源[1]。目前，开发和利用风能的主要形式是大规模并网风力发电。对风速准确预测可以减少电力系统运行成本和旋转备用，提高风电穿透功率极限，有利于调度部门及时调整计划，从而减轻风电对电网的影响[2—3]。

国内外用于风速预测建模的主要方法有：物理方法[4]、统计学方法[5]、空间相关性法[6]、卡尔曼滤波法[3]、随机时间序列法[7]、人工神经网络法[8]和模糊逻辑法[9]等。上述方法对风电场短期风速预测的平均绝对误差为10%～40%[10]。风速由于日周期和季周期均不确定，表现为典型的非平稳时间序列，传统的基于信号平稳性的预测方法难以达到满意的效果。本文针对风速时间序列的特点，提出将双树复小波多尺度分解与最小二乘支持向量机相结合的混合建模方法，对其进行预测分析。

1 原理和方法

1.1 双树复小波

双树复小波变换(DTCWT)是由Kingsbury在1998年提出的[11]，因其具有良好的方向选择性、近似平移不变性、计算效率高以及重构效果好等特点，已经被广泛应用于图像的降噪、分割、分类以及工业生产的各个领域。双树复小波变换是将复小波的实部和虚部分离，采用2组并行实数滤波器组来获取实部和虚部的小波变换系数，通过实数的小波变换实现了复小波变换，解决了复小波变换不能完全重构的问题，双树复小波变换过程如图1所示。树A和树B分别代表复小波的实部和虚部，分别采用不同的滤波器组。

h0(n)和h1(n)分别是树A的低通滤波器和高通滤波器，其尺度函数和实小波函数为

图1 双树复小波变换

(1)

g0(n)和g1(n)分别是树B的低通滤波器和高通滤波器，其尺度函数和实小波函数为

(2)

一维双树复小波可以表示为

φ(t)=φh(t)+jφg(t)

(3)

1.2 最小二乘支持向量机

最小二乘支持向量机(LSSVM)算法是标准支持向量机的一个变形，它将支持向量机求解二次规划问题转换成求解线性方程组，避免了不敏感损失函数，大大降低了计算的复杂性[12—13]。LSSVM的函数估计问题可描述为求解如下问题。设l个样本可表示为：(x1,y1)，(x2,y2),…，(xl,yl)∈Rn×R。利用高维特征空间构造最优决策函数y(x)=ω·φ(x)+b来拟合样本集。式中：φ(x)为从输入空间到高维特征空间的非线性映射；ω为权值向量；b为偏置。利用结构风险最小化原则，将回归问题转化为有约束的二次优化问题：

(4)

式中：xi为输入量；yi为目标值；ξ∈R,为误差变量；φ(xi):Rn→Rnh为核空间映射函数；ω∈Rnh；γ为可调参数；ξi为松弛因子。

引入拉格朗日函数

(5)

式中αi是拉格朗日乘子。根据极值存在的必要条件

(6)

得

(7)

消去ω和ξi，

(8)

根据Mercer条件，使用核函数K(x,xi)，LSSVM回归估计可表示为如下形式：

(9)

2 建模步骤

本文提出将双树复小波与最小二乘支持向量机相结合的方法，对风速时间序列进行建模预测。

1)利用双树复小波对风速时间序列进行多尺度分解。原始风速时间序列按照公式(10)进行分解。

Ψ(t)=φh(t)+jφg(t)

(10)

分解过程中需要选择合适的双树复小波滤波器组合，不同的滤波器组合在分解同一非平稳时间序列时会有不同的结果。常用的双树复小波滤波器组合见表1。

2)依据表1，采用不同滤波器组合对原始风速时间序列进行多尺度分解，最大可分解层数n与输入样本量有关。通过对分解后不同频段子带的混叠能量进行比较，从而得到最优滤波器组合及其对原始风速时间序列分解时的最佳分解尺度。

表1 双树复小波滤波器组合

3)依据最小二乘支持向量机对经双树复小波多尺度分解后的高频子带和低频子带分别建立预测模型。对式(4)进行求解，从而得到最小二乘支持向量机预测模型的回归估计。最小二乘支持向量机对不同频段的子带进行建模时应根据数据样本的特点选择合适的核函数，再通过交叉验证法得到合适的核参数。常用的核函数有：

①线性内积核函数

K(x,y)=x·y

(11)

②多项式内积核函数

K(x,y)=[(x·y)+1]d

(12)

③径向基内积核函数

K(x,y)=exp[-‖x-y‖2/σ2]

(13)

将基于最小二乘支持向量机的不同频段子带预测模型的预测值进行等权求和，得到最终预测结果。建模流程如图2所示。

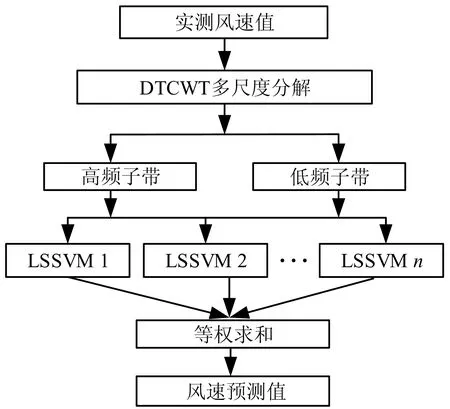
图2 预测建模流程

3 应用实例分析

3.1 风速数据

本文选取甘肃省酒泉地区大型风电场2017年5月1日至2017年10月31日所测的日平均风速数据作为训练样本，共130组；选取2017年11月1日至2017年11月30日的日平均风速数据作为预测样本，共20组，如图3所示。

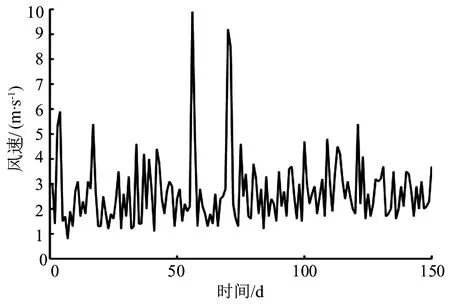
图3 风速实际测量值

3.2 双树复小波多尺度分解

首先，选择不同的双树复小波滤波器组合对风速时间序列进行多尺度分解，对风速时间序列做n层双树复小波变换。其次，确定多尺度分解时的最佳分解尺度。对分解后不同尺度上的高频子带和低频子带进行分析和比较，确定最优分解尺度下的滤波器组合。最后，利用最佳滤波器组合对风速时间序列进行多尺度分解。利用双树复小波对非平稳时间序列进行分解时，双树复小波滤波器组合有6种，见表1。

依据表1中的滤波器组合，对图3所示的风速实际测量值进行多尺度分解，最大分解尺度为6。表2中s表示复杂度，n1—n6表示不同分解尺度下各子带的混叠能量比，通过混叠能量比可以检验最佳滤波器组合。

由表2可见，利用不同滤波器组合对风速时间序列进行多尺度分解时，3号滤波器组合高频子带混叠能量比变化范围为-25.1至-26.2，低频子带混叠能量比变化范围为-24.8至-25.7。

表2 双树复小波不同尺度混叠能量比

表2中，3号滤波器组合混叠能量比变化范围明显低于其他滤波器组合，因此该滤波器组合具有最好的平移不变性。以下利用该滤波器组合对风速时间序列进行双树复小波多尺度分解。分解结果如图4所示，其中，a1、a2和a3为高频子带，b1、b2和b3为低频子带。

3.3 混合模型预测

依据双树复小波多尺度分解后高频和低频子带的变化规律，选径向基用内积核函数建立预测模型，利用交叉验证法确定核参数。

依据公式(13)确定当均方根误差为0.024时，核参数σ=0.25，γ=32。高频子带预测结果如图5所示。

图4 双树复小波多尺度分解

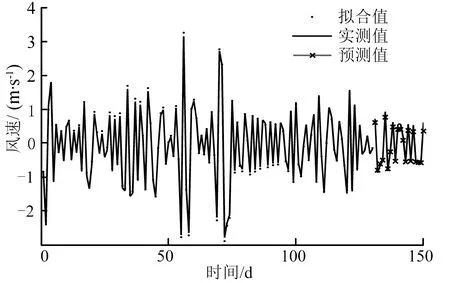
(a)a1子带预测结果

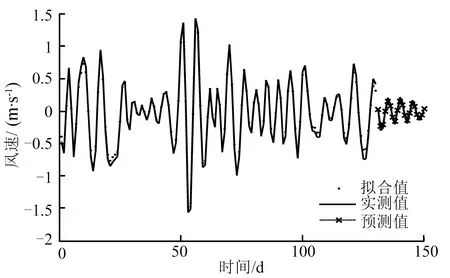
(b)a2子带预测结果

(c)a3子带预测结果图5 高频子带预测结果

依据公式(13)确定当均方根误差为0.031时，核参数σ=0.003 9，γ=512。低频子带预测结果如图6所示。

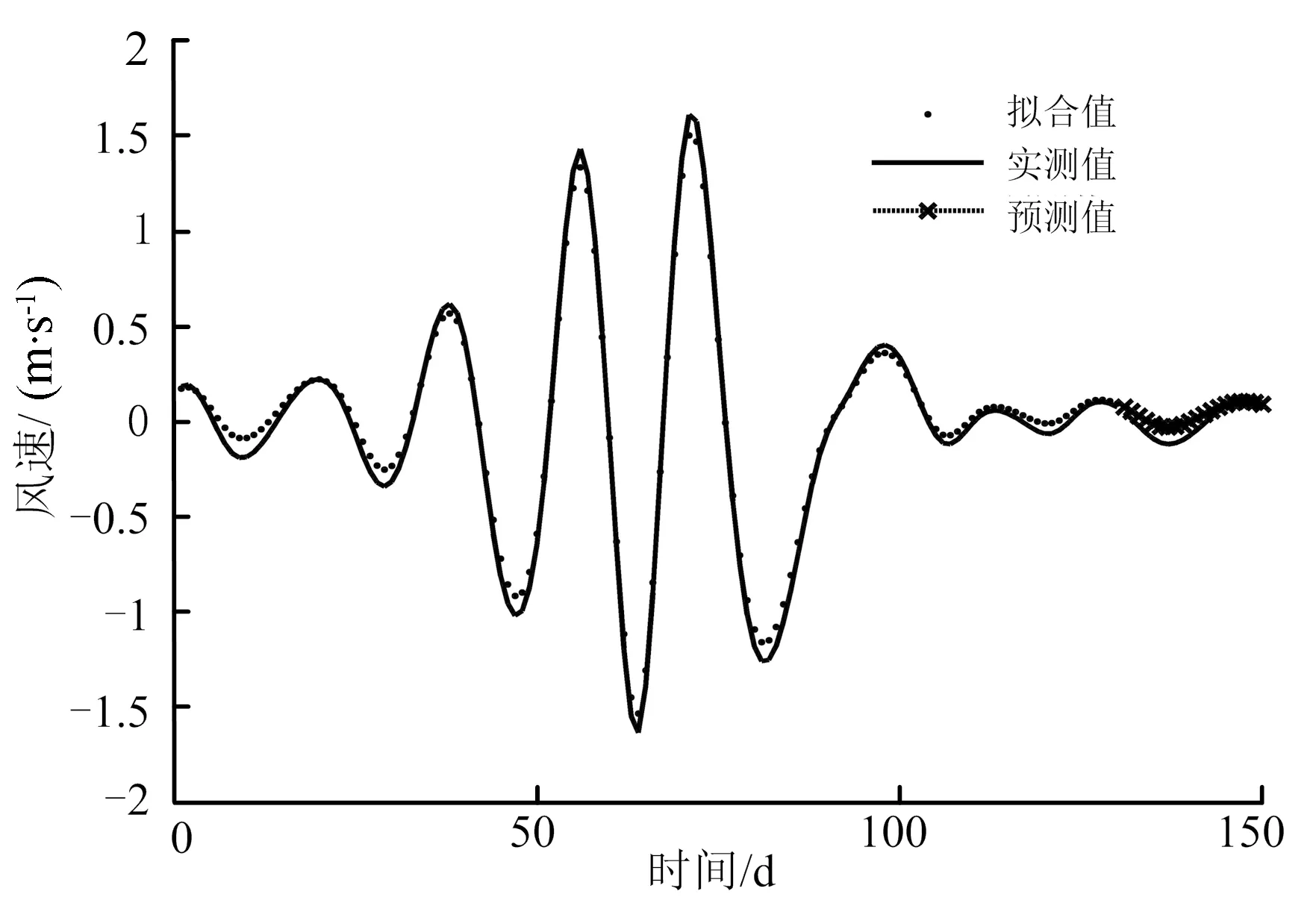
将各子带的预测值进行等权求和得到预测模型的最终预测结果。为了验证混合模型的有效性，再利用EMD-LSSVM模型和WT-LSSVM模型进行预测[14—15]。各模型预测结果见图7。

3.4 误差分析

分别选用平均绝对误差(MAPE)和均方根误差(MSE)作为性能指标。

(a)b1子带预测结果

(b)b2子带预测结果

(c)b3子带预测结果图6 低频子带预测结果

图7 各模型预测结果对比

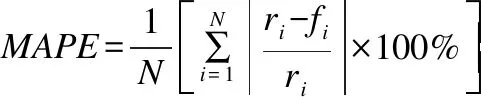
(14)

(15)

式中：ri为原始风速值；fi为预测风速值；N为预测值样本数。

双树复小波与最小二乘支持向量机相结合的预测模型(DTCWT-LSSVM预测模型)、EMD-LSSVM预测模型以及WT-LSSVM预测模型的平均绝对百分误差以及均方根误差见表3。

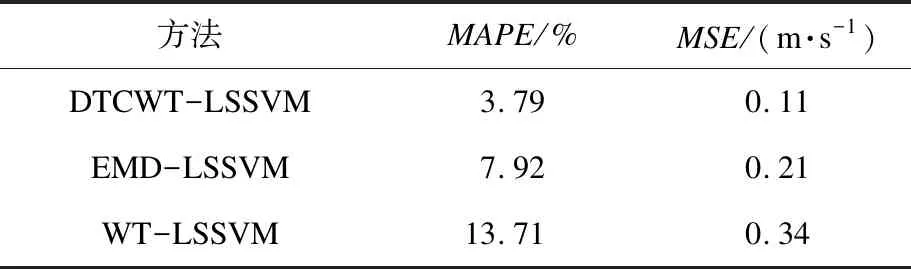
表3 误差分析

可以看出，3种预测模型的MAPE变化范围为3.79%至13.71%，MSE变化范围为0.11 m/s至0.34 m/s。其中，DTCWT-LSSVM模型的预测误差最小，其次是EMD-LSSVM模型，而WT-LSSVM模型的预测误差最大。

4 结论

本文利用双树复小波与最小二乘支持向量机相结合的方法建立风电场短期风速预测模型。预测值与真实值之间的平均绝对误差和均方根误差表明，双树复小波与最小二乘支持向量机相结合的预测模型与其他两种预测模型相比预测误差最小，具有较高的预测精度，对于非线性、非平稳时间序列进行预测建模行之有效。利用该模型计算所得风电场短期风速预测值，综合考虑风电场附近的气温、气压、湿度以及发电机组自身损耗等因素，结合人工神经网络可以建立风电场短期输出功率预测系统。