拉格朗日乘数法在经济中的应用

李帅

（河南师范大学，河南 新乡 453007）

拉格朗日乘数法是解决最优化问题的重要方法之一。由于在经济学中都是具体的实际问题，比如，消费者效用最大化、成本最小化等，它们的最值是否存在是一目了然的，所以拉格朗日乘数法在经济最优化中有着广泛地应用。

一、拉格朗日乘数法在消费者效用最大化上的应用

实例1 已知某消费者的效用函数为U=X1X2,两商品的价格分别为,P1=4,P2=2消费者的收入为M=80。现在假定商品1的价格下降为P1=2。求由商品1的价格P1下降所导致的替代效应，使得该消费者对商品1的购买量发生多少变化？

解 该问题可以转化为两个极值问题，首先求在原来价格不变的情况下的效用大小。

二、拉格朗日乘数法在成本最下化上的应用

这个问题的拉格朗日函数为：

联立求解得：

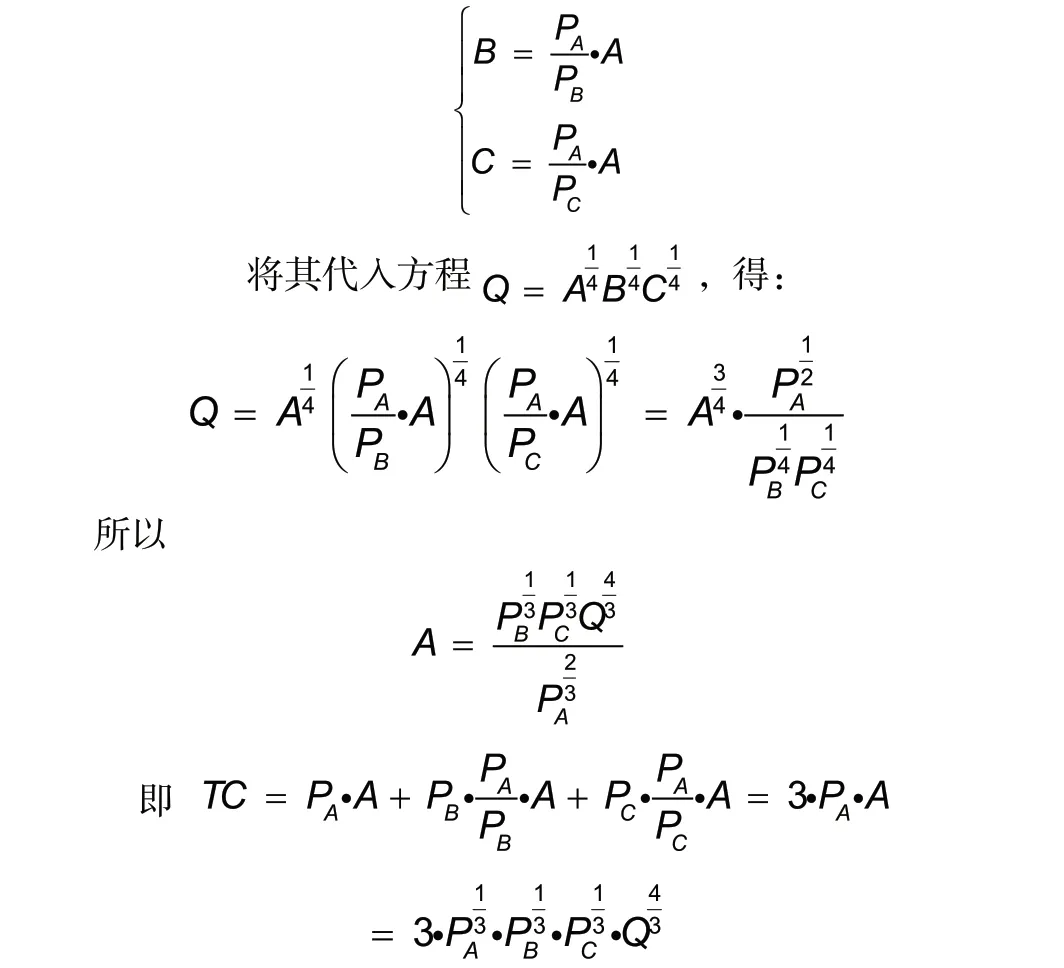
三、小结

本文列举了拉格朗日乘数法在经济最优化中应用的两个实例。从中可以看出，在经济学中涉及到有约束条件的最值问题可以用拉格朗日乘数法来完成。因此，在解决某些经济问题时，可以利用数学知识的工具，从而起到事半功倍的作用。