深度学习在初中数学教材解读中的认识——以《关于原点对称的点的坐标》课堂教学为例

广东省广州市南沙榄核第二中学 江汉标

一、把握教材要有高度

课程标准对教材的定位是“源于教材，但要高于教材”，这是教师在解读教材、设计教学时必须遵照的准则。教师在解读教材过程中要做到胸有成竹，要领悟编委对文本编排的意图，要清晰例题的地位和作用，要明白并处理好习题与例题的关系，还要搞清 “探究、思考、归纳”等教学环节的作用。

例如，本节课教材中设置了“探究”“归纳”“例2”以及“练习”四个学习环节，编委的意图就是要求学生通过操作——猜想——检验的实践过程，积累数学活动的经验。直角坐标系中关于原点对称的点的坐标的关系在学生经历由具体到抽象地认识问题的过程中通过操作、观察、归纳得到。从深层次来看，编委要求学生从点坐标与图形变换的角度揭示中心对称与轴对称之间的关系，培养观察、分析、合作与探究交流的学习习惯，体验事物的变化之间是有联系的。所以，笔者事先要求学生采取小组合作的形式对以下内容进行知识储备及预习：

（1）复习全等三角形的判定及性质；

（2）复习点坐标与长度的关系；

（3）复习在平面直角坐标系中关于坐标轴对称的点坐标的规律；

（4）探究环节中你能得到哪些结论？与之前所学的知识有哪些关联？

（5）例2可以有哪些做法？这些做法有什么异同？

当学生完成课前预习环节后，他们对教材内容的认识、对例题的理解以及对本节课的作用与意义就有了初步的认识，这对学生迅速把握课本的核心内容，掌握数学核心思想将起到关键的铺垫作用。

二、处理教材要有广度

每一个知识点不是孤立的、片面的个体，而是整个知识体系的一环或一点，所以在解读教材时不能孤立地看待各个数学知识点，而应把它放到整个章节或整个知识系统中去解读，要善于引导学生把各个知识点放在整体结构中去学习，了解并建立它们之间的关联与区别。同时还要引导学生建立数学与生活的联系，体会数学与其他学科的关系，从而扩大学生学习数学的视角，夯实学生深度学习的基础。

例如，本节课是在前两节中心对称的学习基础上来研究关于原点对称的点的坐标的规律。由于中心对称和平移、轴对称、旋转一样，都是全等变换的一种，因此它们不仅在变换与坐标的关系上有很多相似之处，而且在关系的探究视角、方法上也有不少相似之处。所以本节课所运用的探究方式与学生对关于坐标轴对称的点的坐标的关系的探究方式是一致的，那就是数形结合，先假设后印证。因此，在“探究”环节，笔者是这样处理的：

（课本P68探究）如图，在直角坐标系中，作出下列已知点关于原点O的对称点，并写出它们的坐标。这些坐标与已知点的坐标有什么关系？

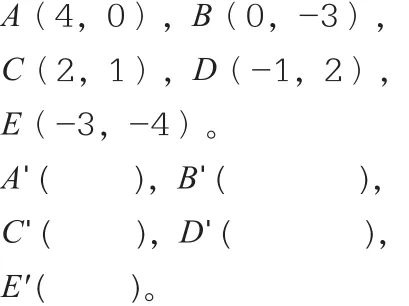
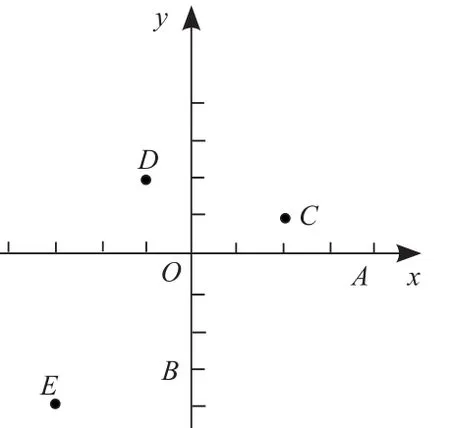
小组讨论内容：

（1）两个对称点所处的象限有什么关系？

（2）两个对称点的横坐标的符号有什么关系？纵坐标呢？

（3）两个对称点的横坐标的绝对值有什么关系？纵坐标呢？能否以点E为例，用全等知识进行说明？

首先让学生观察关于原点对称的点的坐标之间的特征，然后以小组合作的形式讨论老师提出的问题，引导学生从坐标与长度的关系、全等三角形的性质与证明等方面找准本节课的核心内容，最后通过小组汇报总结的形式，让学生得出它们之间的规律，掌握从特殊到一般的数学思想方法。

三、解读教材要有深度

解读教材还要深挖教材，反复钻研教材上的知识点，细致到每一句话、每一幅图、每一道题，仔细推敲教材所呈现的数学知识和数学方法，从而领悟编委对教材编排的意图。

例如，在本节课前，学生已经系统地学习过平移、轴对称、旋转、全等、坐标与长度的关系等知识，并能熟练掌握了数形结合的数学思想。所以从教材的编排来看，编委希望教师采用类比教学，根据建构主义，从学生已有的对关于坐标轴对称的点的坐标的关系的学习基础上展开教学。

笔者引导学生尝试用新学规律简便快捷地画图，并结合解题过程让学生归纳方法，然后精选以下题目：

1.如图，平行四边形ABCD的对角线交点在原点O上，已知A点坐标为（-3，2），则C点坐标为（ ）

A.（2，-3）

B.（-3，-2）

C.（3，-2）

D.（3，2）

2.如图，阴影部分组成的图案既是关于x轴成轴对称的图形，又是关于坐标原点O成中心对称的图形。若点A的坐标是（1，3），则点M和点N的坐标分别是（ ）

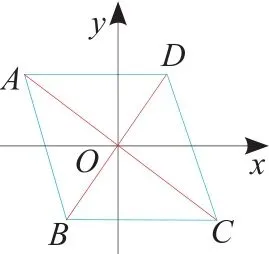
A．M（1，-3），N（-1，-3）

B．M（-1，-3），N（-1，3）

C．M（-1，-3），N（1，-3）

D．M（-1，3），N（1，-3）

3.点P（a，4）关于原点对称的点Q（3，b），则a+b＝____ 。

4.已 知 点 A（-2，3） 和 点 B（2，-3），则A，B两个点的位置关系是____________。

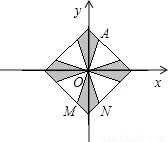
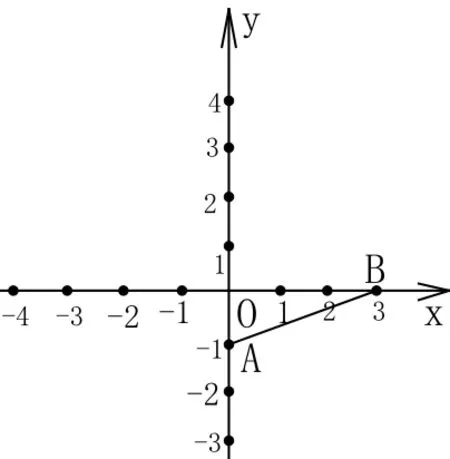
5.如图，利用关于原点对称的点的坐标的特点，作出与线段AB关于原点对称的图形。

6.在直角坐标系中，将点（-2，3）关于原点的对称点向左平移2个单位长度得到的点的坐标是（ ）

A.（4，-3）

B.（-4，3）

C.（0，-3）

D.（0，3）

A.1 B.2 C.3 D.4

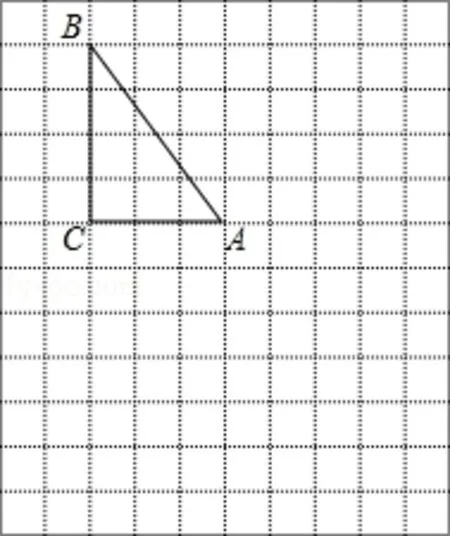
8.在下列网格图中，每个小正方形的边长均为1个单位。在Rt△ABC中，∠C=90°，AC=3，BC=4。

（1）试在图中作出△ABC以A为旋转中心，沿顺时针方向旋转90°后得到的图形△AB1C1；

（2）若点B的坐标为（-3，5），试在图中画出直角坐标系，并标出A、C两点的坐标；

（3）根据（2）的坐标系，作出与△ABC关于原点对称的图形△A2B2C2，并标出B2、C2两点的坐标。

通过这样处理，让学生在运用新知识的同时，渗透平行四边形、中心对称、象限、不等式组、方程组、平移、旋转、整体代换等内容和方法，让学生感受各种知识、方法的融合。

解读教材不是照搬教材，它对教师提出了更高的要求。深度学习需要老师在充分领悟教材意图的基础上，立足教材，整合教材内容，深入挖掘教材内涵，对教材进行二次加工，引导学生在更深层次掌握教材的核心内容，把握数学核心思想与方法。同时要注意的是，深度学习不是减少学生的学习任务，更不是降低学生的学习标准，而是对学生的学习提出更高的标准。