特定约束下一类二元多项式最值问题的初等解法

湖北省武汉职业技术学院商学院(430074) 邹 峰

文[1]中给出一类双对称二元二次方程式的最值问题的解法,笔者就这一问题深入研究,给出特定的二元二次方程式的约束下,巧用三角换元,求函数f(x,y)的最值,给出其统一解法,下面给出四类函数f(x,y)的表达式应用举例,然后给出几个推论和一个推广.

下文的特定约束条件是指：实数x,y满足ax2+bxy+ay2=c,其中a,c∈R+,b∈R且2a＞b.以下,我们考虑在如上的特定约束条件下,求函数f(x,y)的最值,且f(x,y)是常见的二元一次或二元二次多项式等.

由ax2+bxy+ay2=c,考虑待定系数k1,k2∈R+,满足k1(x+y)2+k2(x-y)2=c,可得(k1+k2)x2+2(k1-k2)xy+(k1+k2)y2=c,即解得整理可得可设θ∈R解得令于是可设x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,其中λ1,λ2∈R+,代入方程ax2+bxy+ay2=c,可得然后代入f(x,y)进行求最值,笔者视为统一解法.

第一类若实数x,y满足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b,b≠0),求函数f(x,y)=x2+y2的最大值M和最小值m.

例1(2016年河北高中数学预赛第7题)已知实数x,y满足x2+xy+y2=3,则x2+y2的取值范围.

解设x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,λ1,λ2∈R+,由统一解法可得λ1=1,则所以x2+y2=2cos2θ+6sin2θ=2(1+2sin2θ)∈[2,6].

例2已知实数x,y满足2x2-3xy+2y2=3,则x2+y2的最大值M和最小值m.

解设x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,λ1,λ2∈R+,由统一解法可得则故当θ=0时,M=6,当

推论若实数x,y满足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b),则x2+y2的最大值M和最小值m.当b＞0时,当b＜0时,

第二类若实数x,y满足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b,b≠0),求函数f(x,y)=ax2-bxy+ay2的最大值M和最小值m,称为一类双对称二元二次方程式的最值问题.

例3已知实数x,y满足x2-xy+y2=1,求x2+xy+y2的最大值M和最小值m.

解设x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,λ1,λ2∈R+,由统一解法可得则故x2+xy+y2=当θ=0时,M=3,当

例4已知实数x,y满足3x2-5xy+3y2=10,求3x2+5xy+3y2的最大值M和最小值m.

解设x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,λ1,λ2∈R+,由统一解法可得则故当θ=0时,M=110,当

推论若实数x,y满足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b),则ax2-bxy+ay2的最大值M和最小值m.当b＞0时,当b＜0时,

第三类若实数x,y满足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b,),求函数f(x,y)=rx2+sxy+ty2的最大值M和最小值m.

例5已知实数x,y满足x2+xy+y2=1,

(1)求x2+2xy+3y2的最大值M和最小值m.

(2)求x2-2xy-3y2的最大值M和最小值m.

解(1)设x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,由统一解法可得则故

当sin2θ=-1时,当sin2θ= 1时,

(2)λ1=λ2=1,则x=+sinθ,y=故x2-2xy-3y2=当sin(2θ+φ)=1时,当sin(2θ+φ)=-1时,

推论1 若实数x,y满足x2+xy+y2=1,则rx2+sxy+ty2的最大值M和最小值m分别为

其中r,s,t∈R,且满足若r=t=1时,s≠1;若r=t=0时,s∈R,若s=0,r与t都不为0.

推论2若实数x,y满足x2-xy+y2=1,则rx2+sxy+ty2的最大值M和最小值m分别为

其中r,s,t∈R,且满足若r=t=1时,s≠-1;若r=t=0时,s∈R,若s=0,r与t都不为0.

例6 已知实数x,y满足2x2+xy+2y2=5,求3x2+2xy+y2的最大值M和最小值m.

解设x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,λ1,λ2∈R+,由统一解法可得λ1=1,则故

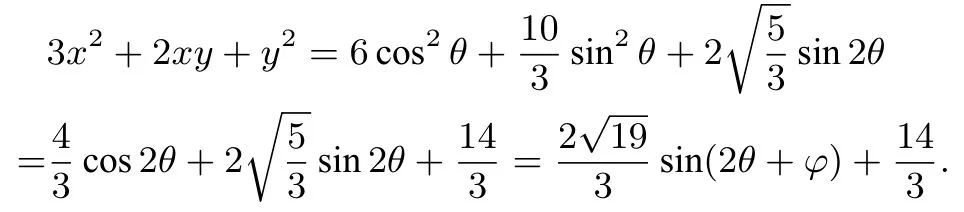
当sin(2θ+φ)=1时,当sin(2θ+φ)=-1时,

推广若实数x,y满足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b),则rx2+sxy+ty2的最大值M和最小值m分别为

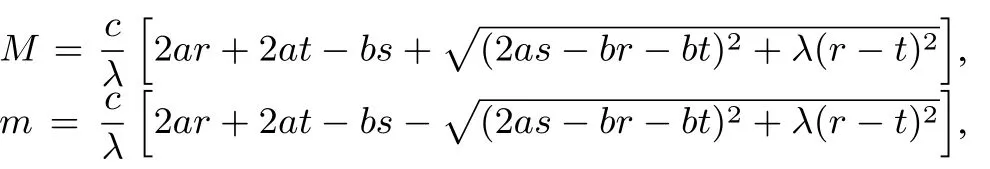
其中λ=(2a+b)(2a-b),r,s,t∈R,且满足若a=r=t时,b≠s;若r=t=0时,s∈R;若s=0,r与t都不为0.

第四类若实数x,y满足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b,),求函数f(x,y)=r(x+y)3+s(x+y)2+t(x+y)+w的最大值M和最小值m.

例7已知实数x,y满足x2+xy+y2=6,求x2y+xy2-x2-2xy-y2+x+y的最大值M和最小值m.

解设x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,λ1,λ2∈R+,由统一解法可得则由x2+xy+y2=6得xy=(x+y)2-6,故x2y+xy2-x2-2xy-y2+x+y=xy(x+y)-(x+y)2+x+y=[(x+y)2-6](x+y)-(x+y)2+x+y=(x+y)3-(x+y)2-5(x+y).令f(t)=t3-t2-5t,f′(t)= 3t2-2t-5= 0,得

第四类问题解题思路如下：

若实数x,y满足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b,),求函数f(x,y)=r(x+y)3+s(x+y)2+t(x+y)+w的最大值M和最小值m.其中r,s,t∈R,且满足r,s,t至多有二个为0.

第一步,设x=λ1cosθ+λ2sinθ,y=λ1cosθ-λ2sinθ,λ1,λ2∈R+,由统一解法可得则

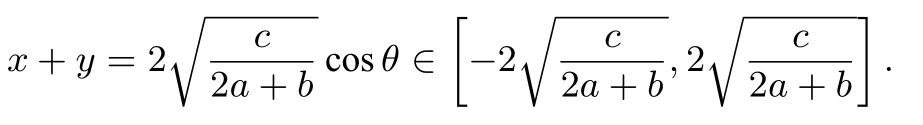
第二步,令

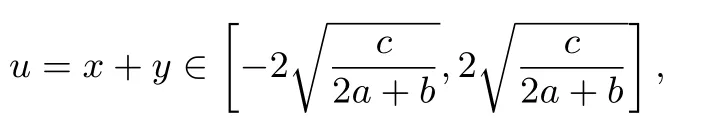
则f(u)=ru3+su2+tu+w,求导f′(u)=3ru2+2su+t=0,在命题的过程中,考虑s2≥3rt及然后求其最值.

练习

(1)已知实数x,y满足2x2+xy+2y2=5,求-3x2+2xy-y2的最大值M和最小值m.

(2)已知实数x,y满足求f(x,y)=的最大值M和最小值m.

总结上述同一条件已知实数x,y满足ax2+bxy+ay2=c,(a,c∈R+,b∈R且2a＞b,),求函数f(x,y)的最值,函数f(x,y)的表达式举不胜数,关于其它函数f(x,y)的表达式最值问题下文再研究.