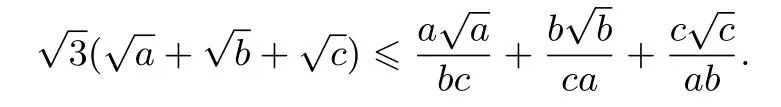例说一个三元分式不等式的应用
2019-05-15河南省南阳师范学院软件学院473061李居之孙文雪
河南省南阳师范学院软件学院(473061) 李居之 孙文雪
河南省南阳理工学院软件学院(473004) 陈 曦
设a,b,c为正实数.由熟知的二元均值不等式a+b≥可以推导出一个常用的三元不等式(a+b+c)2≥3(ab+bc+ca).将其变形可得再将前面的三元不等式作代换a→ab,b→bc,c→ca,即得到另一个常用的三元不等式(ab+bc+ca)2≥3abc(a+b+c).将其变形可得结合前面就可以得到一个不等式链本文主要介绍利用这一左侧不等式来解决一类三元分式不等式,下面举例加以说明:
例1已知正数a,b,c满足求证:ab+bc+ca≥3.
证明因为所以ab+bc+ca≥3.
类似地,还可以证明:
已知正数a,b,c满足求证:a3+b3+c3+6abc≥9.
例2(2004年罗马尼亚布加勒斯特数学竞赛题)已知正数a,b,c满足,ab+bc+ca=1,求证:
证明
类似地,还可以证明:
设a,b,c>0,求证:
此即为1963年莫斯科数学竞赛题,也即为著名的Nesbitt不等式.
例3 (《数学教学》问题869)a,b,c>0,求证:
证明
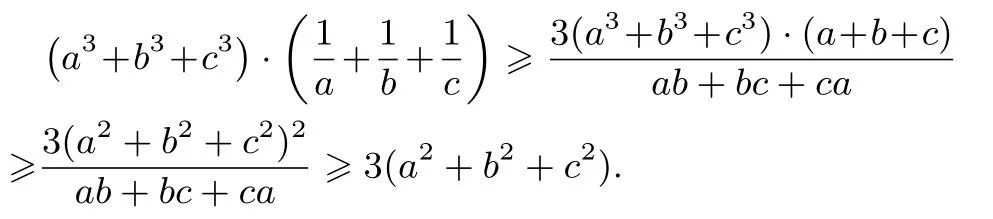
两边同时除以ab+bc+ca,即得
评注问题的原证明通过构造函数,利用函数的单调性证明了其技巧性较高且不易想到,而这一证法只用了三次局部放缩,便完成了证明,避免了原证明中较为复杂的技巧.
类似地,还可以证明《数学通报》问题2251:
设a,b,c>0,求证:
例4设a,b,c>0,求证:
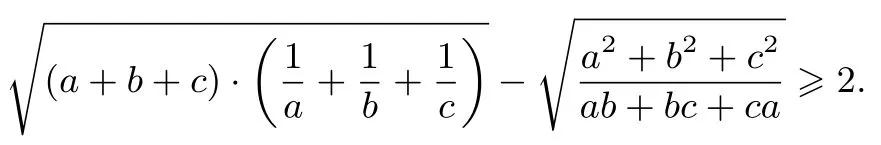
证明

评注此题是安振平老师在新浪博客中提出的4853号问题,可能改编自《数学教学》问题1032:设a,b,c>0,求证:
例5 已知正数a,b,c满足ab+bc+ca=3,求证:
证明

评注此问题改编自《数学通讯》问题304题.
类似地,还可以证明:已知正数a,b,c满足a+b+c=3,求证:
例6 (2012年伊朗竞赛题)已知正数a,b,c满足ab+bc+ca=1,求证:
证明