有心圆锥曲线的统一定义及性质
2019-05-15广东省佛山市顺德国华纪念中学528311张永久
广东省佛山市顺德国华纪念中学(528311) 张永久
1.有心圆锥曲线的统一定义
圆、椭圆、双曲线都有对称中心,统称为有心圆锥曲线,它们统一的标准方程为不失一般性,本文中提到的椭圆和双曲线均是焦点在x轴上.
在人教版A版教材-选修2-1中有三处用交轨法生成有心圆锥曲线,具体如下:
第41页例3:如图2.2-6,设点A,B的坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积为求点M的轨迹方程.
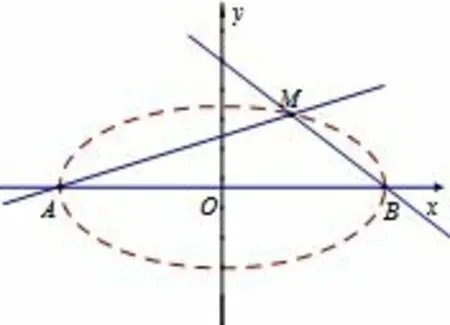
图2.2-6
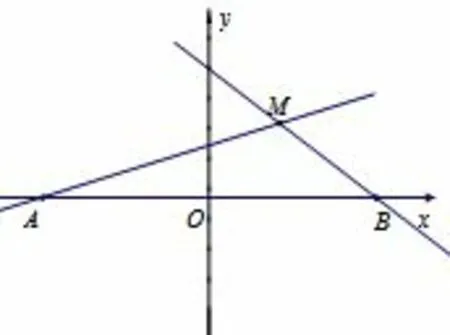
图2.3-5
第55页探究:如图2.3-5,点A,B的坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积为试求点M的轨迹方程.
第80页习题:10.已知△ABC的两个顶点A,B的坐标分别为(-5,0),(5,0),且AC,BC所在直线的斜率之积等于m(m≠0),试探求顶点C的轨迹.
这些知识简单介绍了有心圆锥曲线的生成方式,本文在此基础上探讨有心圆锥曲线的统一定义和相关的性质,以供大家参考.
说明因为有心圆锥曲线上的点与端点重合时,斜率不存在,所以该定义要特别注意两个端点.
设定M(x,y)是曲线上任意一点,由已知得,直线A1M的斜率直线A2M的斜率又因点A1,A2在曲线上,得
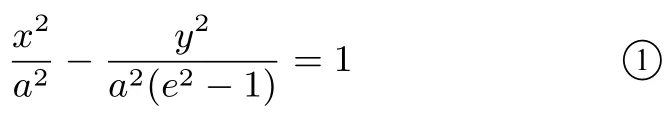
当e=0即e2-1=-1时,方程 ①化为x2+y2=a2,该曲线表示圆;当即a2(e2-1)=c2-a2时,令c2-a2=-b2,方程 ①化为该曲线表示椭圆;令c2-a2=b2,方程 ①化为该曲线表示双曲线.
推论1已知A,B是有心圆锥曲线C:上关于原点对称的两点,点P是曲线C上的任意一点,若直线PA,PB的斜率都存在,则直线PA,PB的斜率之积为
例1 如图1,过坐标原点的直线交椭圆于P,A两点,其中点P在第一象限,过点P作x轴的垂线,垂足为点C,联结AC,并延长交椭圆于点B,求证:PA⊥PB.

图1
证 明设P(x0,y0),B(x1,y1),则A(-x0,-y0),C(x0,0),所以由推论1得,所以因为,kPAkPB=,所以PA⊥PB.
1)进行参数化设计,新型技术需要满足设计师对建筑信息的需求,BIM技术中应用到的软件可以将观察到的对象信息设计成整体的结构状态;
2.有心圆锥曲线的性质
性质1 已知直线l与有心圆锥曲线C:交于A,B两点,AB的中点为M,若直线AB和OM(O为坐标原点)的斜率都存在,则
证明设A(x1,y1),B(x2,y2),则两式相减,得变形,得即
点评用本性质替代点差法,可以简化解题过程.
例2 (2018年高考全国卷III理科)已知斜率为k的直线l与椭圆C:交于A,B两点,线段AB的中点为M(1,m)(m>0).
(2)设F为C的右焦点,P为C上一点,且证明:成等差数列,并求该数列的公差.(略)
证明(1)由性质1得于是又因为M在椭圆C内,得故
推论2已知有心圆锥曲线C:斜率为k1的直线l与曲线C交于A,B两点,若平行于AB的弦的中点的轨迹为CD,设CD的斜率为k2,则
性质2已知有心圆锥曲线C:及C上一点P(x0,y0),则曲线C在点P处的切线方程是
证明方程两边关于x求导,得解得当y0≠0时,曲线C在点P处的切线方程是当y0=0时,曲线C在点P处的切线方程是综上,曲线C在点P处的切线方程是
例3已知椭圆C:直线l:4x-5y+40=0,求椭圆上一点P,使得点P到直线l的距离最小.
解设P(x0,y0),由性质2知曲线C在点P处的切线方程是l′:由题意得l′//l,所以又因为解得由题意得,所求点
推论3已知直线PQ与有心圆锥曲线C:相切于点P,若直线PQ和OP(O为坐标原点)的斜率都存在,则
点评性质2及推论3是高考热点之极点与极线问题.
推论4 已知有心圆锥曲线C:经过点和的切线与C上任一点P的切线相交于点P1和P2,则|P1A1|·|P2A2|=|n|.
证明当n>0时,设由性质2知曲线C在P点处的切线方程为当时,所以当n<0时,设由性质2知曲线C在P点处的切线方程为当时,yP2=所以-n.综上,|P1A1|·|P2A2|=|n|.
性质3 有心圆锥曲线与直线Ax+By+C=0(C≠0)有公共点的充要条件是n(A2m+B2n-C2)≥0.
证明(必要性)由题意得
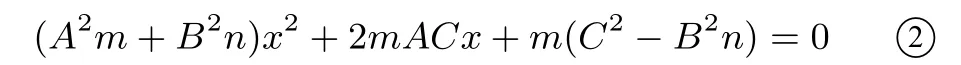
当A2m+B2n≠0时,∆=4m2A2C2-4m(C2-B2n)(A2m+B2n)≥0得
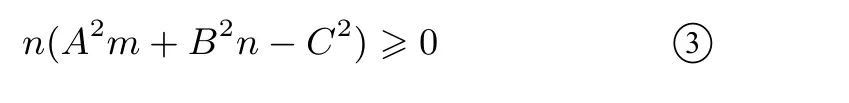
当A2m+B2n=0时,n<0,③式成立.上述证明过程可逆,性质3得证.
点评当C=0时,充分利用几何条件,借助数形结合的思想可以直观地判定曲线与直线的位置关系.
参考人教版A版教材-选修4-4第15页习题第6题,可以得到有心圆锥曲线如下性质:
性质4已知有心圆锥曲线C:O为坐标原点,P、Q为曲线上两动点,且OP⊥OQ,则
证明由将曲线C的直角坐标方程化为极坐标方程,得即()由OA⊥OB可设A(ρ1,θ),则
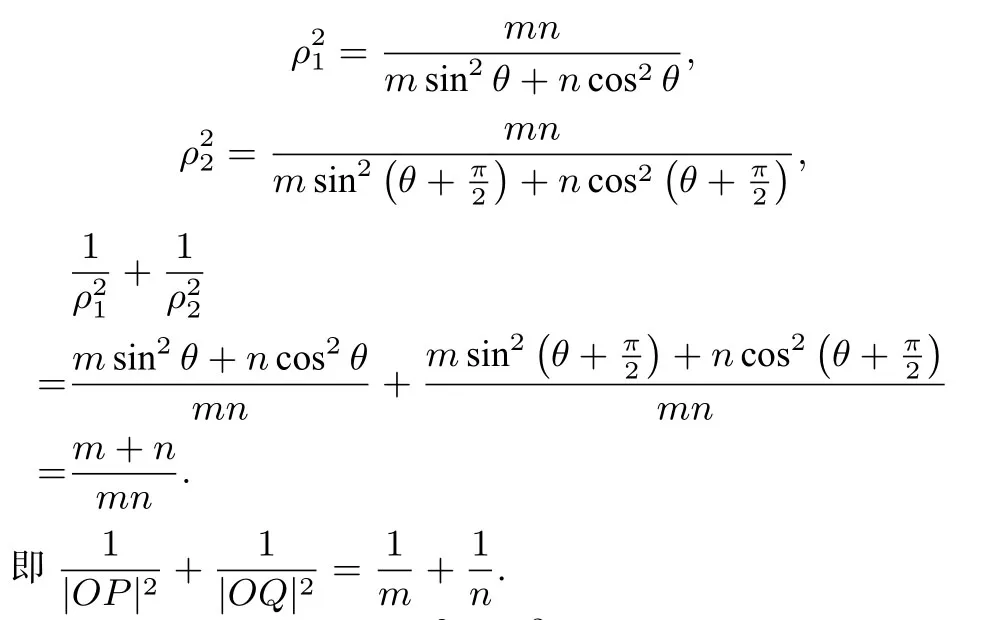
例4已知椭圆C:O为坐标原点,P、Q为曲线上两动点,且OP⊥OQ,求证:
证明由性质4知,得当且仅当|OP|=|OQ|时等号成立.
斜率、离心率、切线、定值和最值是圆锥曲线中非常活跃的元素,也是历年高考的热点.高考中与解析几何相关的试题常考常新,新往往只是形式上,本质上有些相通的地方.有心圆锥曲线有如此结构类似的结论,体现了数学概念的简单性、统一性,结构关系的协调性、对称性,蕴含了数学的奇异美.让人赏心悦目,动人心弦.
