某越野汽车磁流变半主动悬架变论域模糊控制*

庞 辉， 刘 凡， 王 延

(西安理工大学机械与精密仪器工程学院 西安,710048)

引 言

车辆悬架系统的主要功能是吸收由路面不平度引起的振动响应，同时保证轮胎与路面的不间断接触以提高车辆行驶平顺性和操纵稳定性[1-2]。由于半主动悬架(semi-active suspension，简称SAS)兼顾被动悬架(passive suspension，简称PS)的稳定性和主动悬架的自适应能力，能够根据行驶工况实时调整阻尼力大小，实现与主动悬架相近的减振效果，同时无需过多的能量消耗，因而受到了研究人员广泛关注，磁流变减振器(magneto-rheological，简称MR)作为非线性元件被广泛应用于半主动悬架系统中[3]。但是因为其非线性以及磁滞特性，该减振器力学模型难以精确描述[4-5]。Stanway等[6]建立了磁流变减振器的Bingham模型，该模型能很好地描述磁流变减振器阻尼力的时域特性及阻尼力与位移的关系特性，但无法表示在速度较小的区域内阻尼力与速度的关系。Spencer等[7]提出了修正的Bouc-Wen模型，它能较好地描述磁流变减振器的非线性特性，但模型中有过多的参数需要优化辨识，同时由于模型复杂，在实际应用过程中会导致实时性降低，时滞增大。文献[8]针对参数化建模存在的问题建立了一种基于自适应神经模糊的磁流变减振器非参数化模型，同时验证该模型可以高度逼近磁流变减振器实验模型。

针对半主动悬架系统控制器的设计与优化，研究人员开展了大量研究，提出诸如H∞控制[9-10]，滑模变结构控制[11]，自适应反推控制[12]及基于T-S模糊模型的控制[13]等。其中，T-S模糊控制由于结构简单且控制策略不依赖于模型，近年来受到广泛关注。例如，文献[14]针对主动悬架系统控制执行器的延迟和故障不确定性等问题，在满足安全性能约束要求并保证系统渐近稳定性和鲁棒性前提下，设计了一种模糊鲁棒H∞控制器。文献[15]针对非线性半车悬架系统建立了T-S模糊模型，设计了半车主动悬架系统的优化模糊控制器。文献[16]在考虑车身振动及控制时滞条件下，基于T-S模糊模型设计了一种稳定的模糊H∞控制器，实现了悬架系统的渐进稳定以及预期的H∞性能。上述文献所设计的T-S模糊控制器，对悬架性能均有一定程度的改善，但传统模糊控制存在过分依赖专家经验的问题，因此导致所设计控制器控制精度难以保证。针对模糊控制存在的不足，文献[17]提出了变论域模糊控制的思想，在规则不变的前提下，论域随着误差变小而收缩(亦可随着误差增大而扩展)。论域的这种伸缩变化通过调整伸缩因子的大小来实现，目前对于伸缩因子的描述没有统一形式。如文献[18-19]采用函数模型来选择伸缩因子大小，文献[20-21]采用模糊模型来描述伸缩因子变化，但是两种描述都存在一定不足，即函数模型难以在控制过程中精确描述伸缩因子变化，而采用模糊模型会导致伸缩因子的选择完全依赖于经验公式，产生与模糊控制同样的问题。文献[22]针对1/4车辆半主动悬架提出一种基于模糊神经网络的变论域控制策略，并取得了较好的控制效果，但并未研究分析该控制策略对于车身俯仰及其它运动的控制有效性。

为此，针对依据实验数据所建立的磁流变减振器模型及1/2车辆半主动悬架系统，笔者提出一种改进变论域模糊控制器设计方法。通过建立悬架系统的T-S模糊控制器，设计合适的模糊神经网络结构对T-S模糊控制器的两个输入变量论域进行伸缩调整，结合模糊控制的逻辑语言和神经网络的自学习能力，实现对伸缩因子的精准描述。最后通过仿真分析，验证了笔者所提出控制方法的有效性。

1 基于实验数据的MR减振器阻尼特性建模

文中选取路虎极光2016款SUV车所搭载的MagneRide减振器作为研究对象，其内部简化结构如图1左图所示，图1右图为笔者所采用的MagneRide减振器实体。内部结构主要包括磁流变液、活塞、导电线圈、浮动塞以及弹簧。通过调整导电线圈电流大小改变磁流变液中磁性分子排列方式，进而实现减振器阻尼力连续可调。

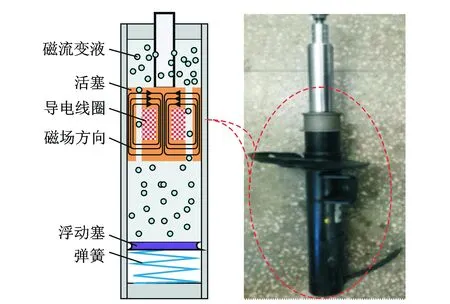
图1 MR减振器实体及内部结构示意图Fig.1 Photograph and inner schematic configuration of the MR shock absorber

为了精确描述MR减振器的非线性磁滞特性，学者们研究了多种力学模型。其中自适应神经网络模糊非参数化模型在避免大量参数识别的同时，能够较为精确描述MR减振器阻尼特性[23]。其结构如图2所示，其中，系统Ⅰ确定不同电压下阻尼力输出等级K；系统Ⅱ描述特定电压下阻尼力与活塞位移和速度之间的非线性关系，F=K×f为减振器输出阻尼力。

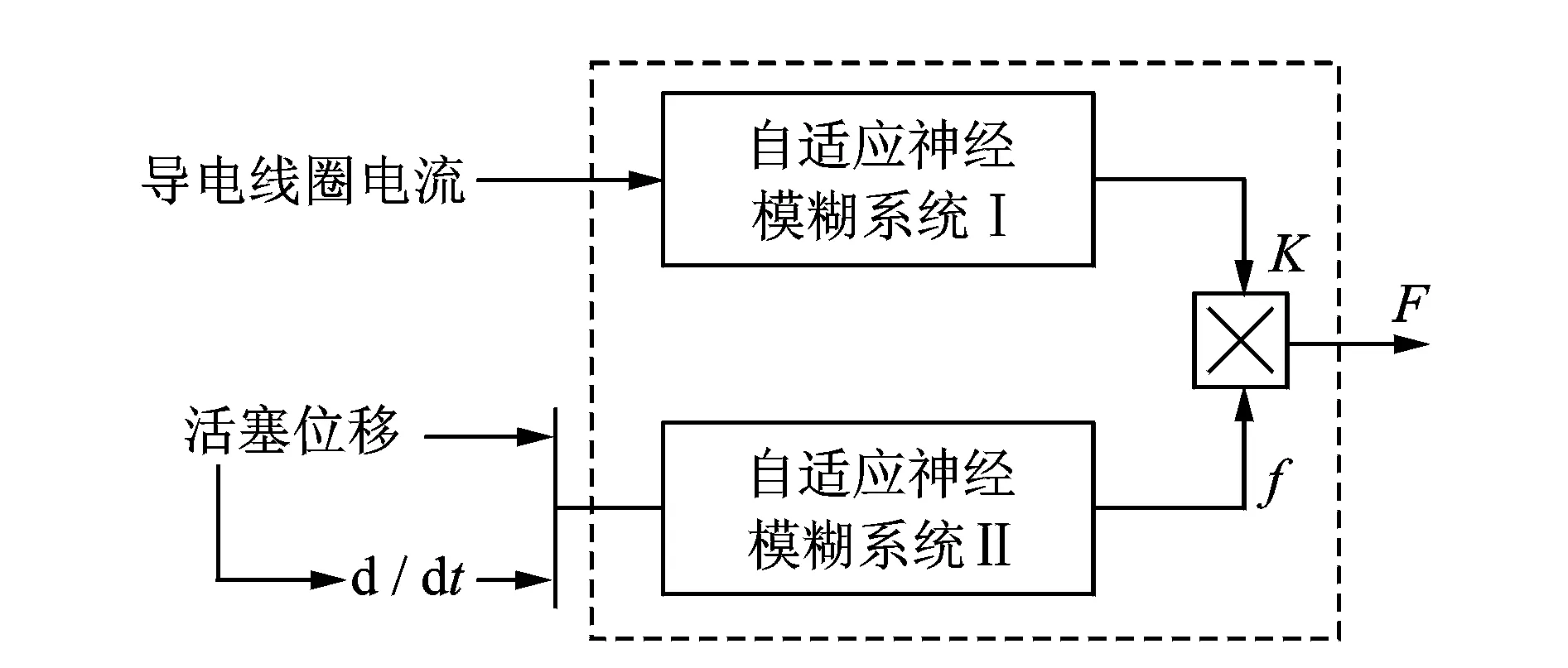
图2 MR减振器自适应神经模糊非参数化模型Fig.2 Non-parametric model of the MR shock absorber based on adaptive neuro-fuzzy

采用如图3所示的最大输出力为20 kN的电液伺服疲劳试验机对笔者所采用的MagneRide减振器进行实验测试，通过分析实验数据并基于MatlabAnfis工具箱对实验数据训练建立如图3所示的MR减振器自适应神经模糊模型。图4为频率2 Hz、振幅25 mm时MR减振器输出阻尼力与活塞位移关系曲线以及对应模型仿真结果。

图3 MR减振器试验台架Fig.3 Testing setup of MR damper

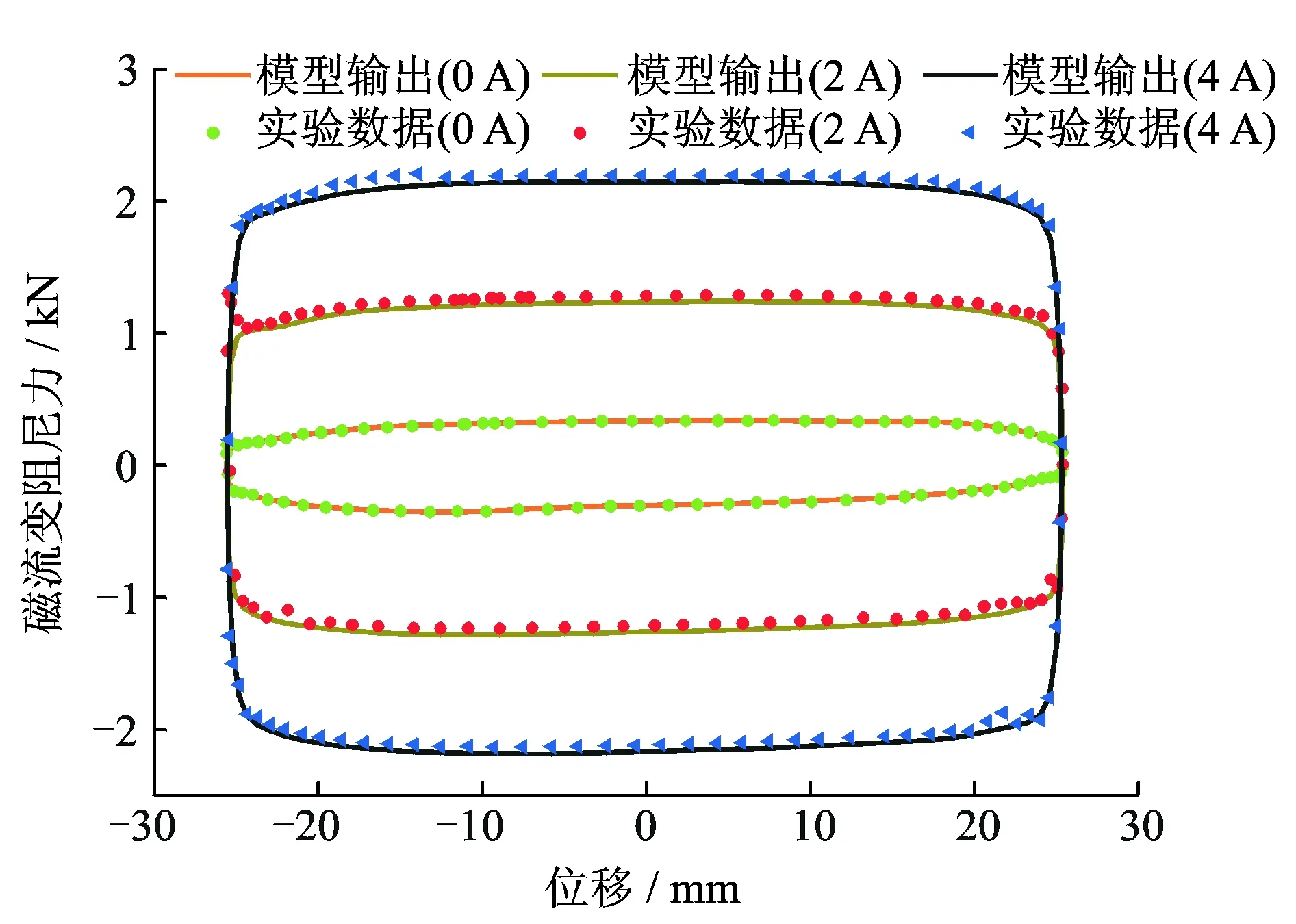
图4 实验数据与模型响应对比Fig.4 Comparison between the identified model and the measured data

2 半主动悬架系统动力学模型

1/2车辆悬架模型包含了车辆动力学分析的主要特征，且结构简单，所以在悬架控制策略的研究中被广泛应用。图5为4自由度1/2车辆悬架系统模型，其中：Is为转动惯量；a，b为前后轴到质心的距离；θ为车身俯仰角；ms为折算到半车模型上的簧载质量；mu f，mu r为非簧载质量；kt f，kt r为轮胎刚度系数；zs，zu f，zu r，qf，qr分别为簧载质量、非簧载质量和路面的绝对位移；kf，kr为悬架的刚度。模型中用线性弹簧代替弹性轮胎，忽略轮胎阻尼；减振器固有阻尼及可变阻尼力代替磁流变减振器，因此前后磁流变减振器阻尼力可表示为

(1)

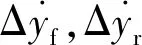
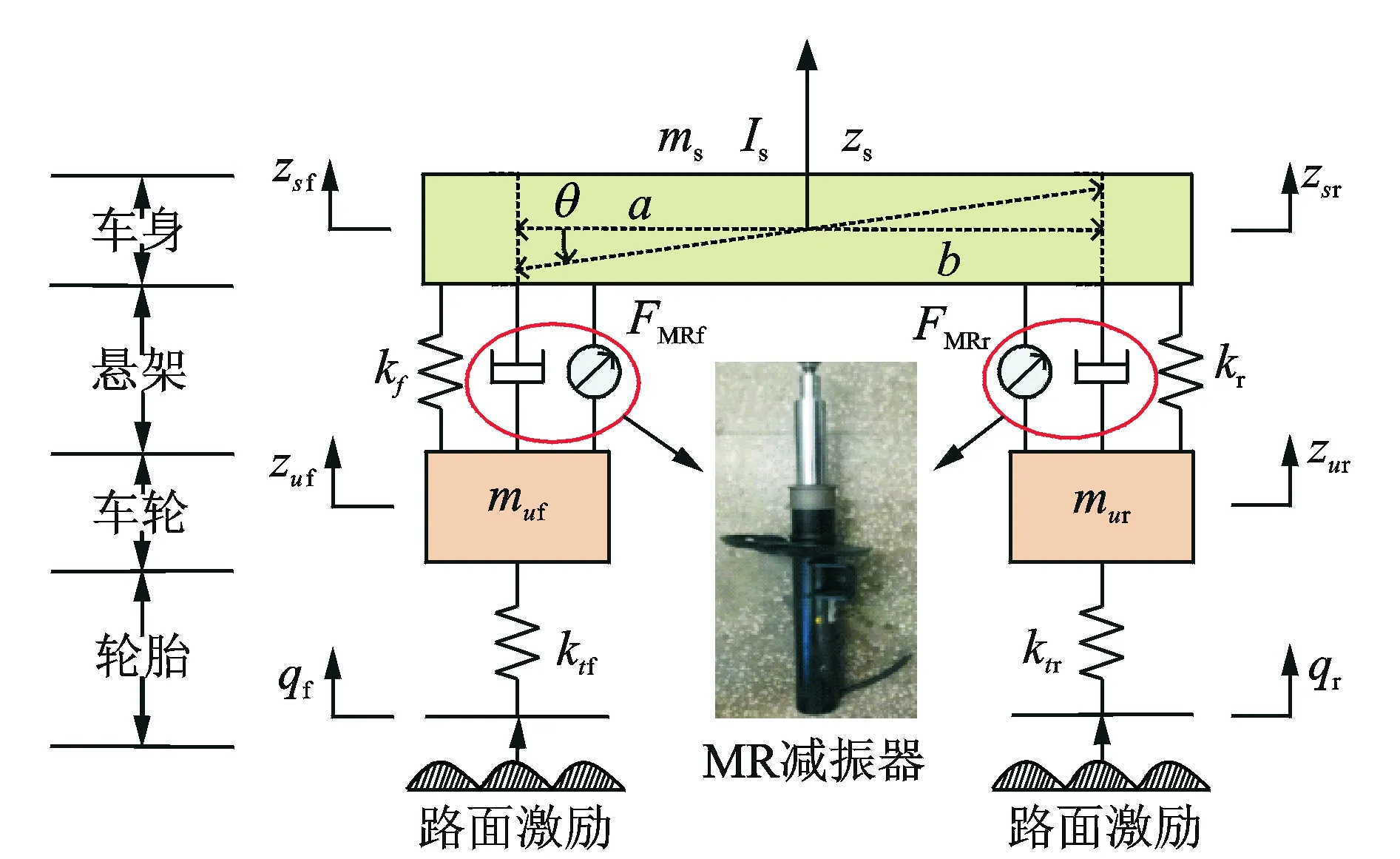
图5 1/2车辆悬架系统模型Fig.5 The half vehicle dynamic model

如图5所示的1/2车辆振动模型中，要求车辆相对于纵垂面完全对称，而且左右车轮下的路面不平度完全一样，即认为车辆是在纵垂面上的振动，对其受力分析如下。

对于前后轴上方的垂直位移有如下关系

(2)

则悬架系统动力学方程为

(3)

3 变论域模糊控制系统设计

3.1 变论域模糊控制基本思想

变论域模糊控制的思想可以描述为：假定Xi=[-Ei,Ei](I=1,2,…,n)代表输入变量xi(i=1,2,…,n)的模糊论域，Y=[-U,U]代表输出变量y的模糊论域。同时{Ail}分别表示模糊语言变量Xi，Y的模糊集合[24]。具体描述如下。

1) 在规则不变的前提下，论域随初始论域[-E,E]通过伸缩因子α(x)变换为[-a(x)E,a(x)E]，如图6所示，a(x)为误差变量x的连续函数。

2) 变论域的思想意味着变量Xi,Y的模糊论域随着输入输出变量xi，y而变化，具体表达形式如式(4)，(5)所示。

其中：变量αi(xi)(i=1，2，…，n)，β(y)分别表示Xi，Y的伸缩因子。

另外，Xi，Y的初始论域定义为原始论域，且采用7个语言模糊子集{NB(负大)，NM(负中)，NS(负小)，ZE(零)，PS(正小)，PM(正中)，PB(正大)}。输入输出模糊论域伸缩变化如图6所示。

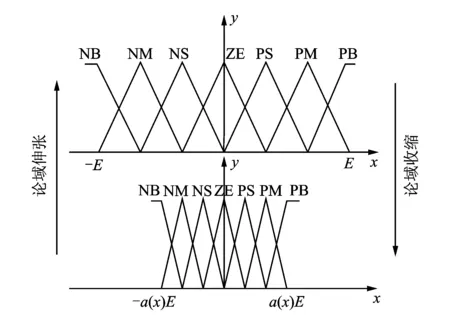
图6 变论域模糊控制基本思想Fig.6 The variation of contracting-expanding universe

文献[25]采用模糊推理来描述伸缩因子的变化，其仿真结果表明，基于模糊推理的变论域模糊控制(variable-universe fuzzy control based on fuzzy reasoning，简称VUFC-FR)算法能够有效地提高收敛速度和控制精度，但是这种控制算法伸缩因子的模糊论域划分不够精确，从而导致控制结果存在误差。针对这一不足，笔者采用模糊神经网络结构来控制伸缩因子的变化，结合模糊推理的语言逻辑性和神经网络的自学习调整优势，通过系统误差分析以及神经网络的自学习调整修正伸缩因子的模糊论域划分。基于模糊神经网络的变论域模糊控制(variable-universe fuzzy control based on fuzzy neural network，简称VUFC-FNN)框图如图7所示，r和y分别代表理想的输入和控制信号，I表示控制电流，FMR为减振器输出阻尼力，e为系统控制误差，并表示为e=r-y。

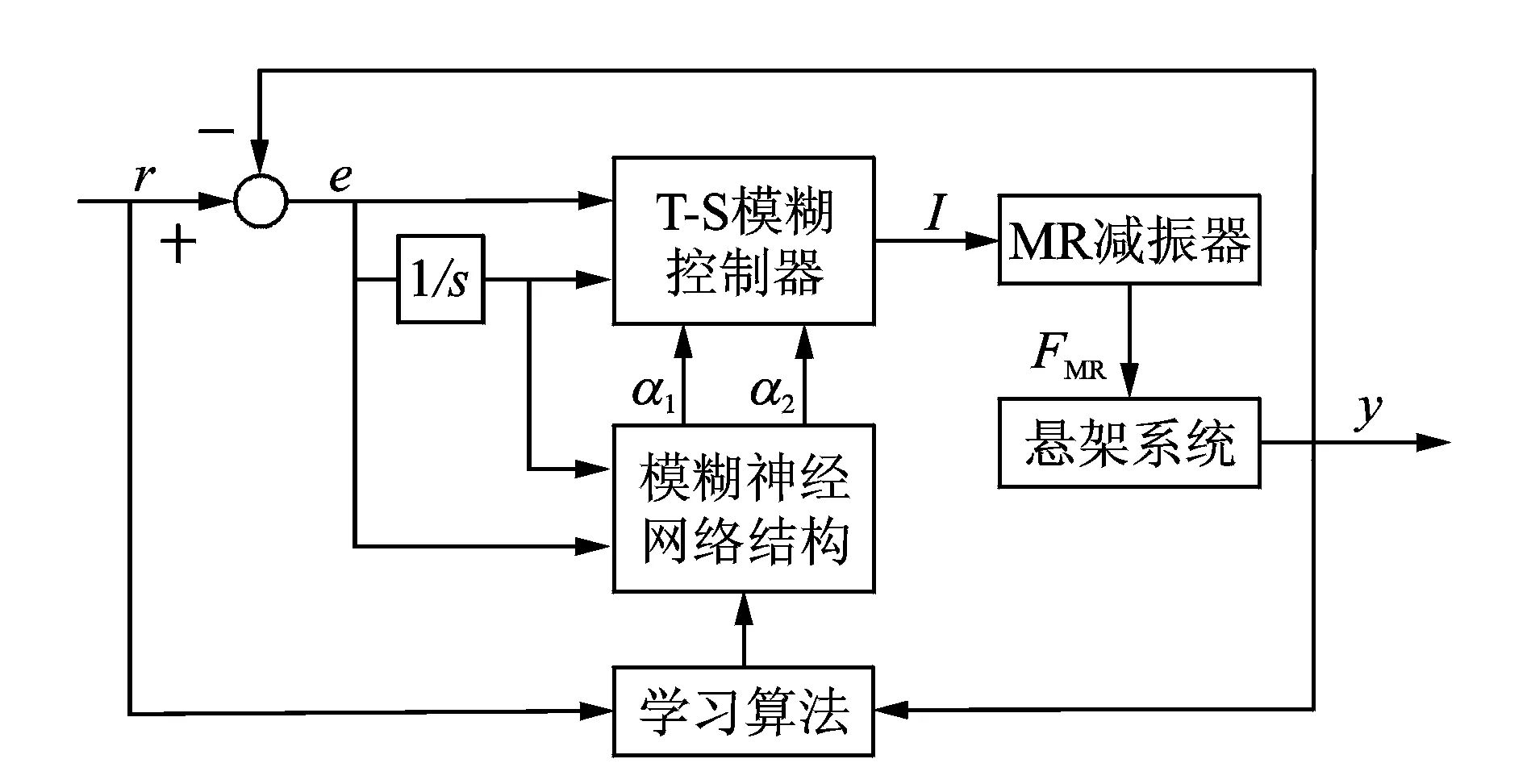
图7 基于模神经网络的变论域模糊控制框图Fig.7 The control block of VUFC based on FNN

3.2 基于T-S模糊模型的变论域控制器设计

T-S型模糊控制器可由如下方程组成：

Ri:如果xi为Ai1，x2为Ai2，…，xj为Aij，…，xn为Ain,那么

gi(X)=ai0+ai1x1+ai2x2+…+aijxj+…+ainxn

(6)

其中：Ri(i=1,2,…,R)为第i条规则；X=[x1,x2,…,xj,…,xn]T为模糊控制器的输入矢量；xj(j=1, 2,…,R)为第j个输入变量；Aij为模糊集合；gi(X)为第i条规则的输出；f(X)为模糊控制器的输出，采用中心平均解模糊方法；μi(X)为第i条规则的定义为乘积形式的满足程度；Aij(xj)为xj对Aij的满足程度；hij(xj)为定义在输入论域上的隶属度函数[26]。

T-S模糊控制器在设计过程中有两个关键性问题：a.确定控制规则数目；b.确定规则后件的系数。确定规则数目的过程，即对输入变量划分的过程，它需要产生合理的子空间。确定控制规则后件系数也就是确定区域作用量的过程。解决这两个关键问题步骤如下。

1) 最优参数。行驶平顺性和操纵稳定性是汽车动力学研究的两个重要领域，悬架系统在协调这两大使用性能方面起着非常重要的作用。在分析悬架诸多影响因子中，选取3个基本参数对悬架性能作评价，分别为车身加速度、悬架动挠度和轮胎动载荷。为了同时满足车辆行驶平顺性和操纵稳定性的要求，建立如式(10)所示的目标函数J

(10)

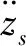
3.3 模糊神经网络伸缩因子设计

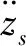
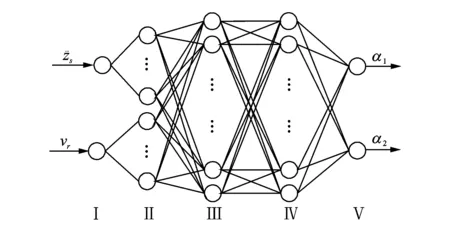
图8 模糊神经网络(FNN)的结构Fig.8 The structure of FNN

网格的Ⅰ，Ⅱ层对应于模糊规则“if”前提，采用高斯型函数作为隶属函数。

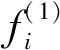
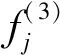
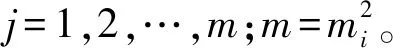
网格的Ⅴ对应解模糊层，采用面积重心法实现解模糊化。该层的输出节点f(5)为调节系统模糊论域的伸缩因子α1，α2，即

(16)

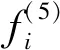
在实现伸缩因子调整的模糊神经网络FNN结构中，输入分量的模糊划分个数mi是预先确定的，则需要学习的参数包括最后一层的连接权ωij(该层对应于伸缩因子模糊控制器的输出论域的中心值，i=1,2；j=1,2,…,m)和Ⅱ层隶属度函数的中心值cij和宽度bij(i=1,2；j=1,2,…,mi)[27]。

上述伸缩因子模糊神经网络是一种多层前馈网络，因此可以采用误差反转的方法设计调整参数的学习算法，从而使系统的实际输出逼近期望输出。设yr和y分别表示期望输出和实际输出，定义误差能量函数E=1/2(yr-y)2，则模糊神经网络的调整参数的自学习算法如式(17)所示

(17)

其中：η>0为模糊神经网络学习速率。

为了验证笔者提出的基于模糊神经网络的变论域模糊控制算法的有效性和稳定性，使用Matlab/Simulink工具箱建立该控制算法的仿真模型，在随机不平路面激励下，选择车身加速度、俯仰角加速度、悬架动行程及轮胎动载荷作为输出测量变量。

4 仿真分析4.1 随机不平路面模型

文中采用白噪声法建立路面模型为

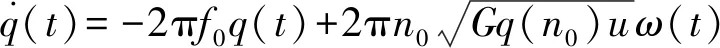
(18)

其中：f0为路面输入的下截止频率；n0为参考空间的频率；Gq(n0)为路面不平度系数；u为车速；ω(t)为白噪声。

Matlab/Simulink仿真所得随机不平路面[28]如图9所示。

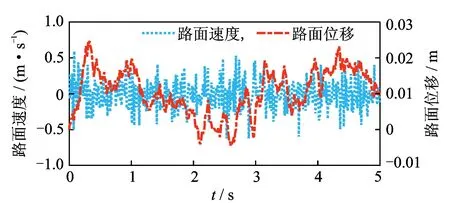
图9 B级路面激励信号Fig.9 The B-class road excitation used for simulation

4.2 仿真验证

文中仿真采用的车辆磁流变半主动悬架参数见表1。

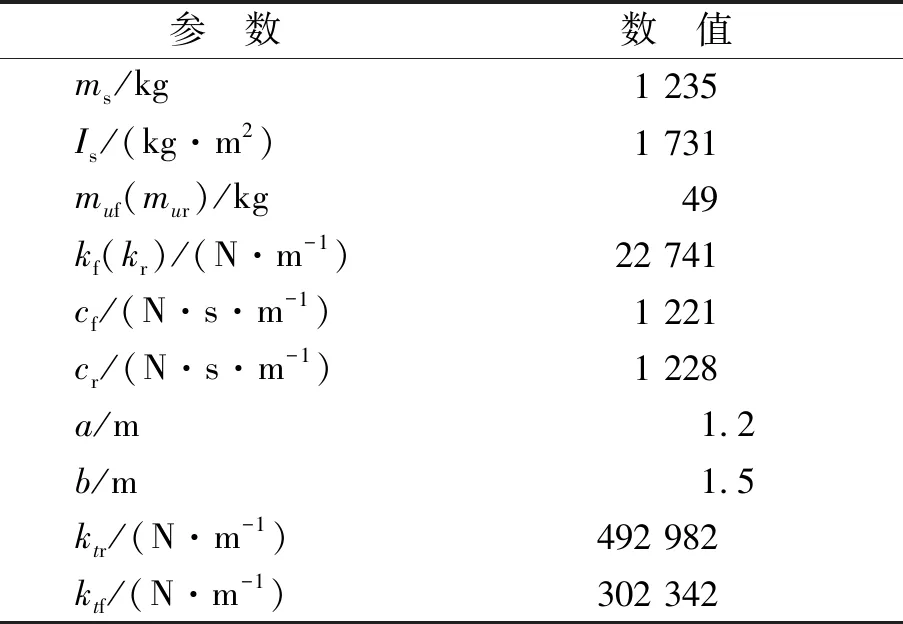
表1 1/2车辆磁流变半主动悬架系统模型参数

在控制仿真中，采用随机路面激励作为输入信号，基于Matlab/Simulink工具箱的改进变论域模糊控制器设计如图10所示。

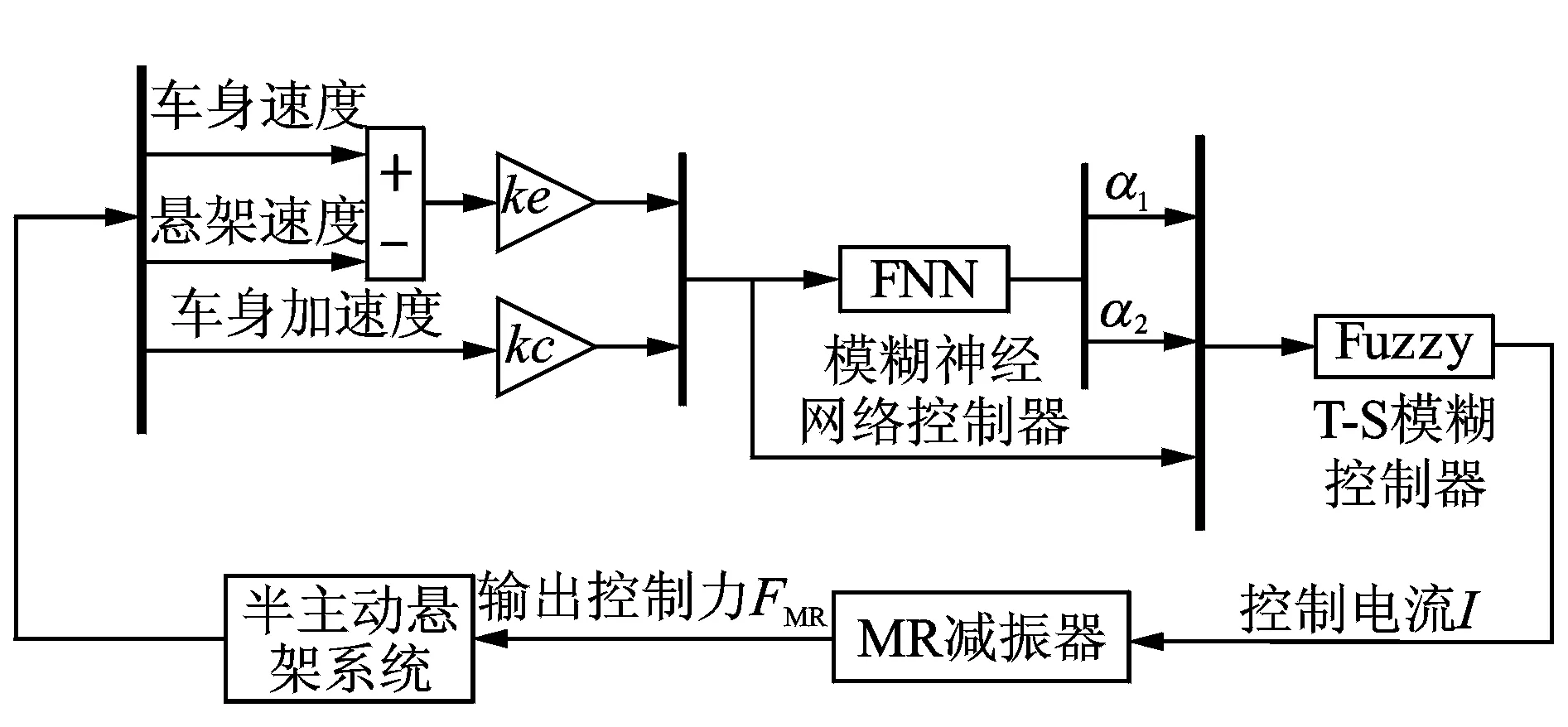
图10 变论域模糊控制系统模型Fig.10 Simulation block diagrams of the enhanced VUFC

图中：ke,kc为T-S模糊控制器比例因子；α1，α2为输入变量伸缩因子。ANFIS采用模糊神经网络控制车身垂向加速度、车身相对速度的论域变化范围。T-S模糊控制器输出为控制电流I，同时I作为MR减振器模型输入，得到控制阻尼力并作用于半主动悬架系统。

仿真条件为B级随机路面，车速为20 m/s。

从图11、图12可以看出，相比于被动和VUFU-FR控制悬架，VUFC-FNN控制的MR半主动悬架车身加速度和俯仰角加速度优化效果明显； 同时在频域响应，车身加速度和俯仰角加速度功率谱密度也得到了较好改善。

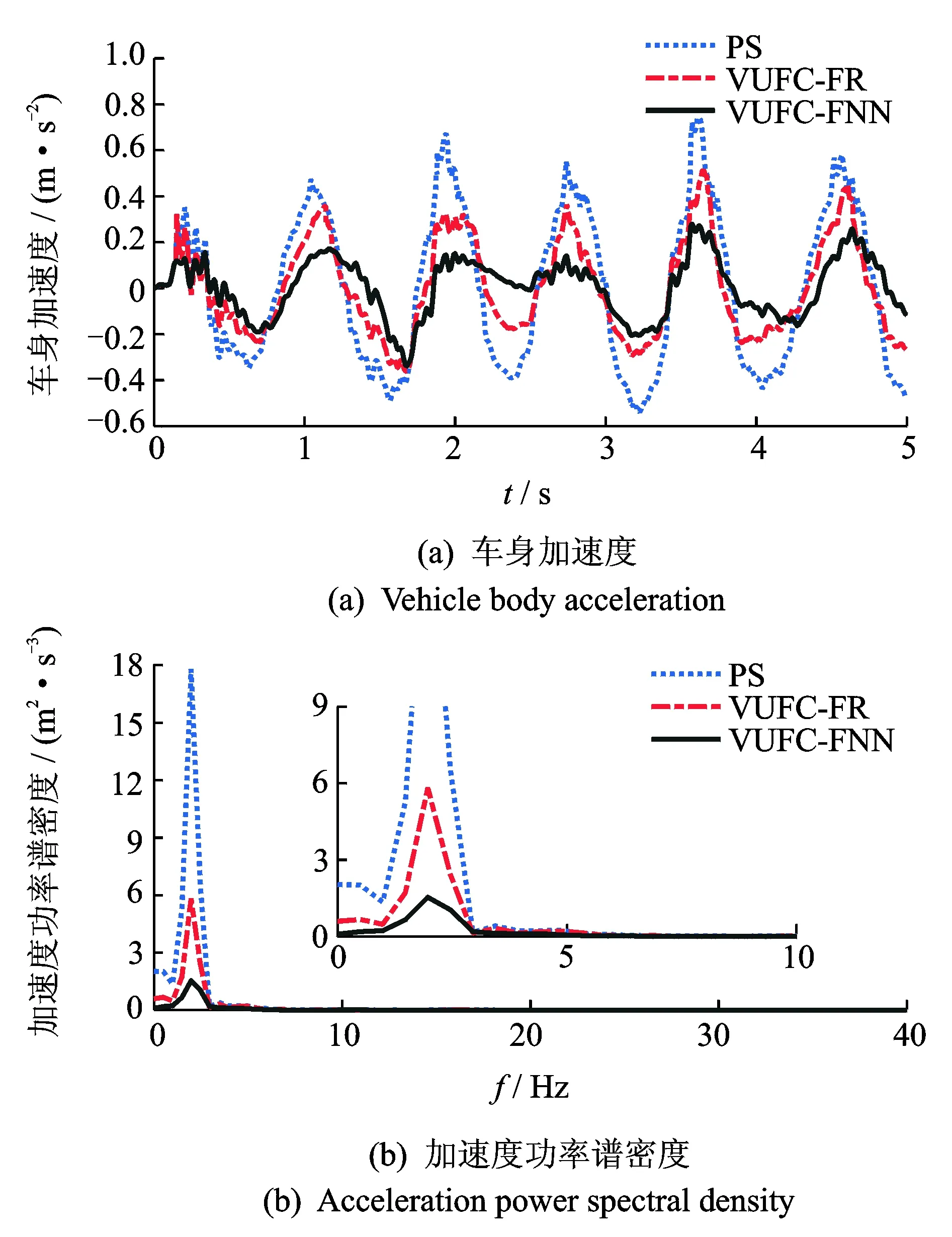
图11 车身加速度响应Fig.11 Response to vehicle body acceleration

从图13可以看出，VUFC-FNN控制算法可有效减小前后轮悬架动行程，防止悬架动行程超出限定范围而导致悬架击穿。从图14可以看出，VUFU-FNN控制MR半主动悬架可有效改善路面作用于轮胎的冲击载荷，提高轮胎寿命同时保证车辆操作稳定性。图15为前后轮MR减振器所产生的阻尼力。

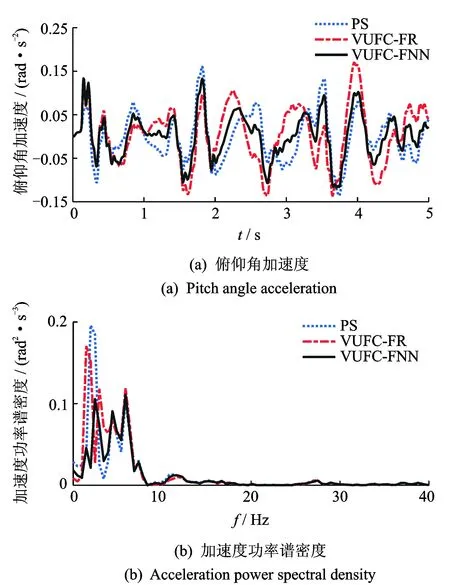
图12 车身俯仰角加速度响应Fig.12 Responses to vehicle body pitch angular acceleration

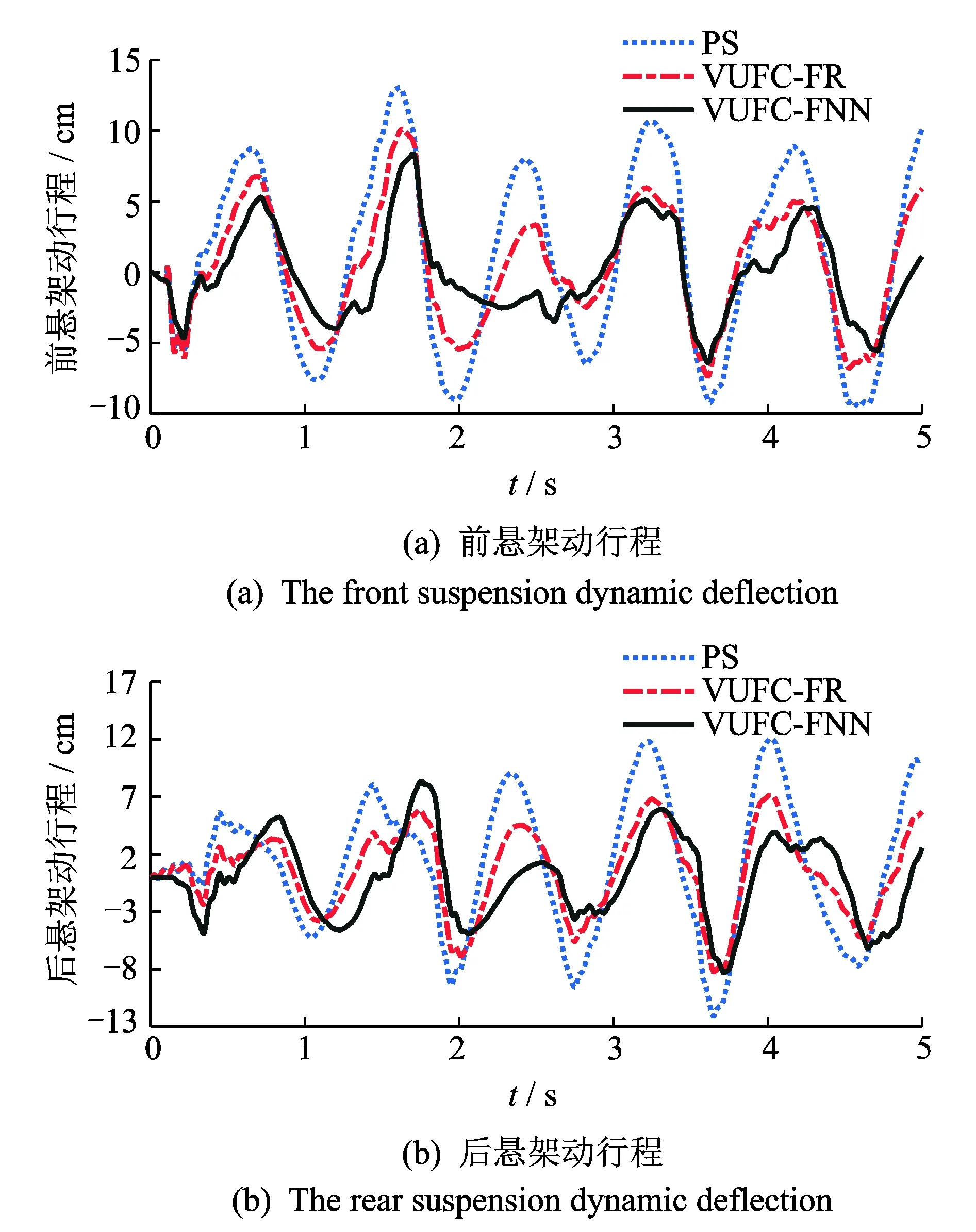
图13 悬架动行程响应Fig.13 Responses to the suspension dynamic deflection

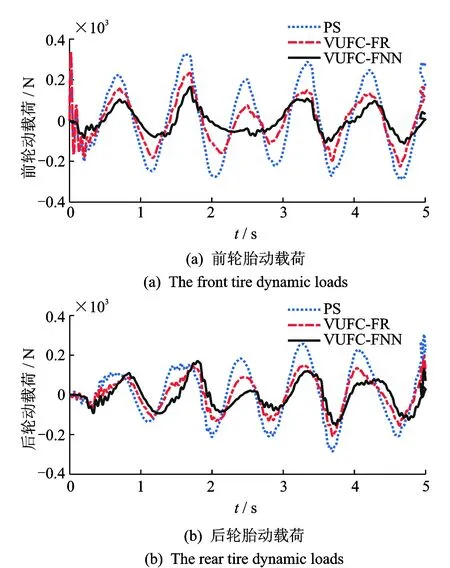
图14 轮胎动载荷响应Fig.14 Response to the tire dynamic loads

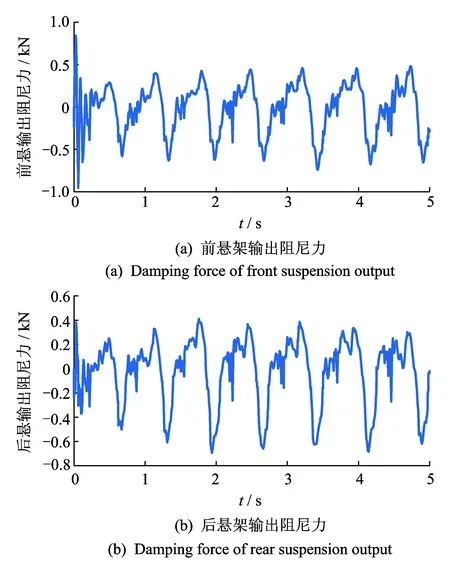
图15 磁流变减振器输出阻尼力Fig.15 Response to the MR damper force

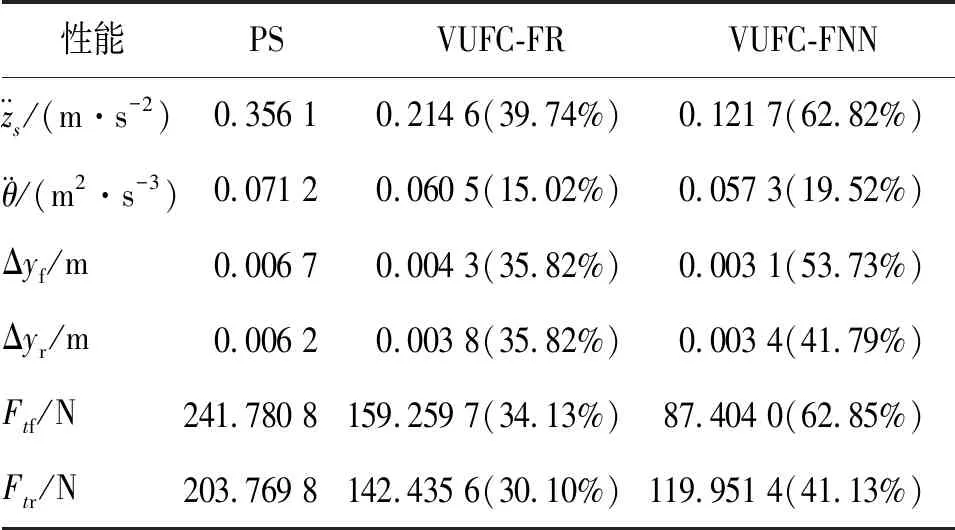
为进一步说明控制算法的有效性，表2列出了被动悬架、VUFC-FR及VUFC-FNN控制悬架在随机不平路面扰动下车身加速度、俯仰角加速度、悬架动行程、轮胎动载荷的均方根值以及优化的百分比。

表2 悬架性能指标均方根值比较

Tab.2 Comparison of RMS values of suspension performance

性能PSVUFC-FRVUFC-FNN¨zs/(m·s-2)0.356 10.214 6(39.74%)0.121 7(62.82%)¨θ/(m2·s-3)0.071 20.060 5(15.02%)0.057 3(19.52%)Δyf /m0.006 70.004 3(35.82%)0.003 1(53.73%)Δyr /m0.006 20.003 8(35.82%)0.003 4(41.79%)Ftf /N241.780 8159.259 7(34.13%)87.404 0(62.85%)Ftr/N203.769 8142.435 6(30.10%)119.951 4(41.13%)

从表2可以看出，VUFC-FNN控制MR半主动悬架在随机不平路面扰动下，各项性能指标均有一定程度的提升，而且优化效果明显优于VUFC-FR控制悬架，说明笔者所提出的VUFC-FNN控制算法能够有效提高车辆行驶平顺性和操作稳定性。

5 结束语

通过建立1/2车辆MR半主动悬架系统动力学模型，考虑随机路况条件的影响，研究了基于模糊神经网络的变论域模糊控制方法，并与被动悬架和基于模糊推理的变论域模糊控制进行比较。研究结果表明，相比于被动悬架，笔者提出的VUFC-FNN控制MR半主动悬架系统各项性能指标均有一定提升。车身加速度和俯仰角加速度分别优化62.82%和19.52%；前后轮悬架动行程和轮胎动载荷分别改善53.73%，41.79%，62.85%和41.13%。基于模糊神经网络的变论域模糊控制能适应路面工况的变化，可有效改善车辆行驶的操作稳定性和乘坐舒适性，且控制效果优于基于模糊推理的变论域模糊控制。