受迫振动中作用力做功的特征分析

王睿博

(电子科技大学信通学院 四川 成都 611731)

王启州

(电子科技大学英才学院 四川 成都 611731)

吴彦旭

(电子科技大学信通学院 四川 成都 611731)

邬劭轶 吴明和 滕保华

(电子科技大学物理学院 四川 成都 611731)

1 引言

受迫振动是物理学中一个重要的内容，在各个大学物理教科书和众多学术文献中均有介绍和讨论[1～5].但是在教科书和相关论文中多是讨论位移共振和速度共振，即讨论通过改变策动力的频率而导致振子系统的振幅、速度等极大的情形，同时对速度共振时系统中各个力的功与共振时速度极大值的相互关系也鲜见讨论.

本文将策动力频率和阻尼系数选作自变量，分别计算在两个不同参数坐标下阻尼力以及策动力和回复力3个力所做的功，并通过分析阻尼力的功与速度共振的相互关系，更深入了解受迫振动中的共振现象.

2 受迫振动中功的表达式

设质量为m，劲度系数为κ，阻尼系数为γ的振子系统，在回复力-κx，阻尼力-γv和策动力F0cos(ωt)3个力作用下做受迫运动，其动力学方程为

(1)

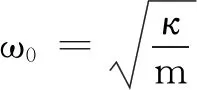
系统达到稳态后，其运动学方程可表示为

x=Acos(ωt+φ0)

(2)

其中A为振幅，φ0为位移的初相，它们分别为[1,2]

(3)

(4)

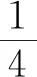
(5)

(6)

(7)

3 受迫振动中作用力做功的特点分析

3.1 速度共振频率下作用力做功的特点

当一个振子系统做受迫振动时，可以通过改变策动力频率来分析系统的共振现象，从而看到人们常说的位移共振、速度共振等物理现象.求解A(ω)和ωA(ω)的极值，可以得到位移共振和速度共振时所对应的两个共振圆频率分别为

(8)

为了深入理解速度共振时系统中的能量转换情况，我们以策动力频率为自变量分别来分析阻尼力以及策动力和回复力等3个力所做的功.

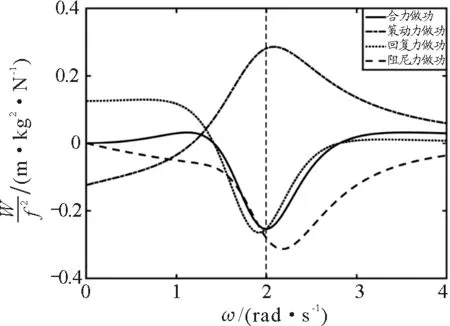
图1 阻尼力、策动力、回复力及合力的做功曲线

图1中的参数分别设定为：阻尼β=0.7 N/(kg·m/s)，固有圆频率ω0=2 rad/s，策动力幅值f=1 N/kg.图中线虚线、点划线和点虚线3条虚线分别代表阻尼力以及策动力和回复力所做的功，而实线代表合力所做的功，平行于纵轴的虚线标记的频率为速度共振圆频率ω0.

可以看出，阻尼力、策动力、回复力等3个分力所做的功都是关于策动力频率的单峰形态，但是做功峰值对应的频率不同，分别位于系统速度共振频率的左右.阻尼力和策动力做功的极值对应的频率大于系统速度共振频率，而回复力做功的极值对应的频率则小于速度共振频率.也就是说，系统处在速度共振频率下，3个分力做的功都不是其极值.

但是在速度共振频率下，策动力和阻尼力在整个过程中始终相互抵消，即

Fdriving=fcos(ω0t)

(9)

fdamping=-2βv=

(10)

这就意味着，在速度共振时，策动力做的正功始终弥补阻尼力的负功，于是此时系统的功完全由回复力决定，即在速度共振时系统相当于处于没有外力的简谐运动状态，使得合力做功为极大值，从而使振子的速度为极大值.从图1可以明显看出，在速度共振时，3个分力做的功在ω0处都不是其极值，但是合力的功在ω0处却是其极值.

3.2 小于或大于速度共振频率时阻尼做功的特点

下面分析策动力频率不等于速度共振频率时，阻尼系数对阻尼力做功的影响.我们以系统阻尼系数作为自变量，可以得到在策动力频率和固有频率保持固定的条件下，阻尼力做功对阻尼系数的依赖关系图.图2为阻尼系数坐标下阻尼力做功的图像，其中参数设置为固有圆频率ω0=2 rad/s、策动力幅值f=1 N/kg.

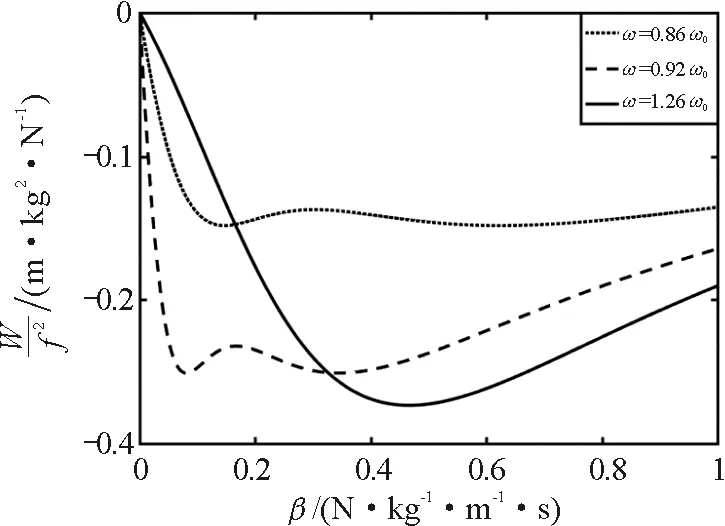
图2 阻尼系数坐标下阻尼力的功

可以发现，在阻尼系数坐标下阻尼力做功的特点比较特殊，其做功曲线呈现出多峰形态，并且峰值对应的阻尼系数各不相同.从图2中点虚线和线虚线可以看出，当策动力频率小于固有频率时，阻尼力做的功是关于阻尼系数的双峰结构，即阻尼力功的极值对应两个不同的阻尼系数，根据阻尼力功的表达式Wf，可以得到双峰的位置和功的极值分别为

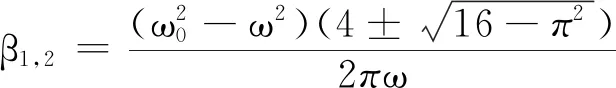
(11)

这表明，阻尼力在两个不同阻尼系数下都会达到其功的极值状态，且极值相等.

当策动力频率大于固有频率时，阻尼力的功呈现单峰形态，如图2中实线所示.

4 结论

本文分别从策动力频率和阻尼系数两个不同角度，分析了阻尼力以及策动力和回复力3个力所做的功，以及阻尼力的功与速度共振的一些细节关系，发现了在速度共振频率下，3个分力的功都不是其极值，但是其合力的功却是极值；而当策动力频率小于固有频率时，存在两个阻尼系数使阻尼力的功都会达到极值状态，从而对共振现象有了更加深入的认识.