基于相关分析和Lempel-Ziv指标的轴承损伤程度识别*

尹建程， 徐敏强

(哈尔滨工业大学深空探测基础研究中心 哈尔滨，150001)

引 言

滚动轴承是旋转机械中最重要的部件之一，因此，在旋转机械工作中滚动轴承的正常运行就显得尤为重要。当滚动轴承发生故障时，其振动信号也会随之发生改变，振动信号中不仅包含了滚动轴承的正常信号，还会含有轴承故障信号。应用相关的技术方法处理、分析滚动轴承的振动信号，就可以识别轴承故障及其严重程度。

近年来，随着信号分析技术的发展，时域、频域和时频域的信号分析方法都广泛应用到轴承健康监测的研究上。例如：均方根值、峭度值、峰值等时域指标被广泛应用到轴承故障诊断中[1-3]，并取得一定的效果。Dyer等[4]研究基于时域统计特征的方法对轴承故障进行诊断。McFadden等[5]使用共振解调的频域方法对轴承进行故障诊断。文献[6-8]分别使用小波分析和经验模式分解的时频域方法对轴承进行分析等。但是，上述的技术方法都是基于线性系统假设的，而轴承在实际运行过程中由于种种原因往往表现出非线性系统特征，因此，这些基于线性假设的方法就无法很好地对轴承出现的非线性故障进行分析。

由Lempel等[9]提出的Lempel-Ziv指标被广泛应用到识别和定量非线性系统信号中不规则成分[10-13]当中。Yan等[14]将Lempel-Ziv指标应用到轴承故障程度的识别中，并取得一定的效果。近年来国内外的许多学者对这个指标在轴承上的使用进行了进一步的研究。Hong等[15]将小波变换与Lempel指标相结合，并使用峭度因子选择最佳的小波分解层计算Lempel指标对轴承损伤程度进行评估。窦东阳等[16]结合经验模态分解(empirical mode decomposition,简称EMD)和Lempel指标对轴承损伤程度进行识别。何雷等[17]将Lempel指标用到局部均值分解 (local mean decomposition,简称LMD)分解层上对某型装甲车变速箱轴承径向磨损程度进行评估。张超等[18]利用LMD和Lempel-Ziv指标对不同载荷和转速下的轴承故障损伤程度进行分析研究。

已有研究结果表明：在单一故障模式下Lempel-Ziv指标能有效区分轴承的损伤程度；但当系统噪声较大时，Lempel-Ziv指标会受噪声影响，导致该指标数值偏大，从而该指标不能有效地区分噪声环境下轴承的损伤程度。因此，笔者提出了基于相关分析的Lempel-Ziv指标计算方法。相比于小波分解、EMD和LMD分解等频率截断的消噪方法，信号通过相关分析，可以在不丢失轴承故障信号频率信息的前提下对轴承信号进行消噪。通过轴承内、外圈的故障数据进行验证，笔者所提方法能有效用于单一故障模式下轴承损伤程度的识别。

1 Lempel-Ziv指标的计算原理

Lempel-Ziv指标是一种有效衡量时间序列复杂程度的工具。为了提高计算效率，Lempel和Ziv对传统的复杂度计算过程进行了简化。Lempel-Ziv指标的计算过程[11-12]如下：

1) 设定初始值Sv,0={},Q0={},CN=0,r=0，令Qr={Qr-1sr}，由于Qr不属于Sv,r-1，则CN(r)=CN(r-1)+1,Qr={},r=r+1；

2) 令Qr={Qr-1sr}，判断Qr是否属于Sv,r-1={Sv,r-2sr-1}，若是，则CN(r)=CN(r-1)，r=r+1，重复步骤2；

3) 若否，则CN(r)=CN(r-1)+1,Qr={},r=r+1，重复步骤2。

Lempel-Ziv指标计算的流程图如图1所示。

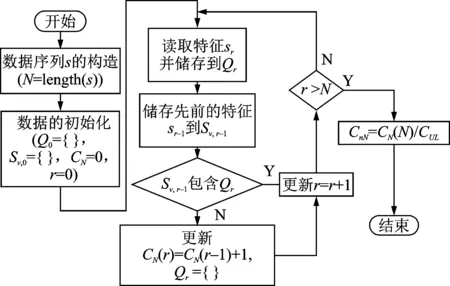
图1 Lempel-Ziv指标计算流程图Fig.1 The flow chart of the Lempel-Ziv

其中Lempel-Ziv指标值的大小受样本的长度影响。为了得到一个相对独立的指标，Lempel和Ziv进一步提出了归一化公式

(1)

(2)

即

(3)

其中：k为SN中元素的个数(对于二进制序列SN，k=2)。

当N值足够大时，归一化公式(1)成立。文献[19]中给出了N的经验取值N≥3 600，称CnN为Lempel-Ziv归一化值。

2 基于相关分析的Lempel-Ziv指标

2.1 自相关分析原理

自相关函数描述了某一信号在不同时刻的相互关系。设某一时刻的信号为x(t)，另一时刻的信号为x(t+τ)，则自相关函数定义[20]为

(4)

工程上采集的信号为离散信号，因此自相关函数的离散形式如式(5)所示

(5)

其中：T为采样长度；N为信号长度；τ为数据时差；l为离散数据间隔。

自相关函数有以下性质：a.调幅信号的自相关函数仍是调幅信号；b.调频信号的自相关函数是调幅信号；c.调幅调频信号的自相关函数是幅值调制及频率调制的[21]；d.随机噪声信号的自相关函数迅速衰减并趋于零。

自相关分析用于轴承信号降噪就是利用自相关函数不改变调幅和调频信号的频率成分，而信号中随机成分的自相关函数是衰减的信号这一性质实现的。当旋转设备出现异常时(如轴承内圈出现剥落、滚动体磨损、齿轮中的某个齿面严重磨损或断齿)，轴承的振动信号表现出调制特性。通过自相关函数分析，这些调制成分被保留下来，而随机的噪声信号迅速衰减。因此，自相关分析能很好地应用到轴承振动信号的消噪中。

2.2 基于相关分析的Lempel-Ziv指标计算流程

噪声会增大系统本身振动信号的复杂度，而当轴承出现不同程度故障时也会改变信号的复杂度，同时随着某些故障程度的加深将增大信号的复杂度。因此，对于这种情况，很难对损伤程度进行识别。所以，对轴承振动信号提前消噪就显得尤为重要。通过上述的介绍，自相关分析能在保留轴承故障特征信号的前提下对信号进行消噪。因此，笔者将自相关分析和Lempel-Ziv指标相结合来对轴承损伤程度进行识别。基于自相关消噪后的Lempel-Ziv指标计算过程为：

1) 将原始信号X进行自相关分析，得到消噪后的数据序列Y；

2) 对序列Y进行0,1编码，得到编码后的序列s；

3) 对序列s计算Lempel-Ziv指标。

具体的流程图如图2所示。

图2 基于自相关的Lempel-Ziv指标计算流程图Fig.2 The flow chart of Lempel-Zivindex based on autocorrelation

3 仿真数据与实验数据验证

为了能说明本算法对轴承磨损程度识别的原理，以及验证笔者所提方法的有效性，分别对仿真数据与实验数据进行计算分析，具体分析结果如下。

3.1 仿真数据验证

仿真数据能够简单、有效的反映Lempel-Ziv指标对轴承磨损程度识别的原理，以及噪声对该指标的影响。通过引入自相关分析算法，使得改进方法在噪声影响下，仍然能够有效识别信号频率的复杂程度。

下面模拟4组信号，其中采样频率为12 kHz，采样点为10 240。

仿真信号的时域波形如图3所示，仿真信号的频域波形如图4所示。

图3和图4中给出仿真信号的时域和频域波形，其中仿真信号x1(t)的时域和频域波形分别如图3(a)和图4(a)所示；仿真信号x2(t)的时域和频域波形分别如图3(b)和图4(b) 所示；仿真信号x3(t)的时域和频域波形分别如图3(c)和图4(c)所示；仿真信号x4(t)的时域和频域波形分别如图3(d)和图4(d)所示。

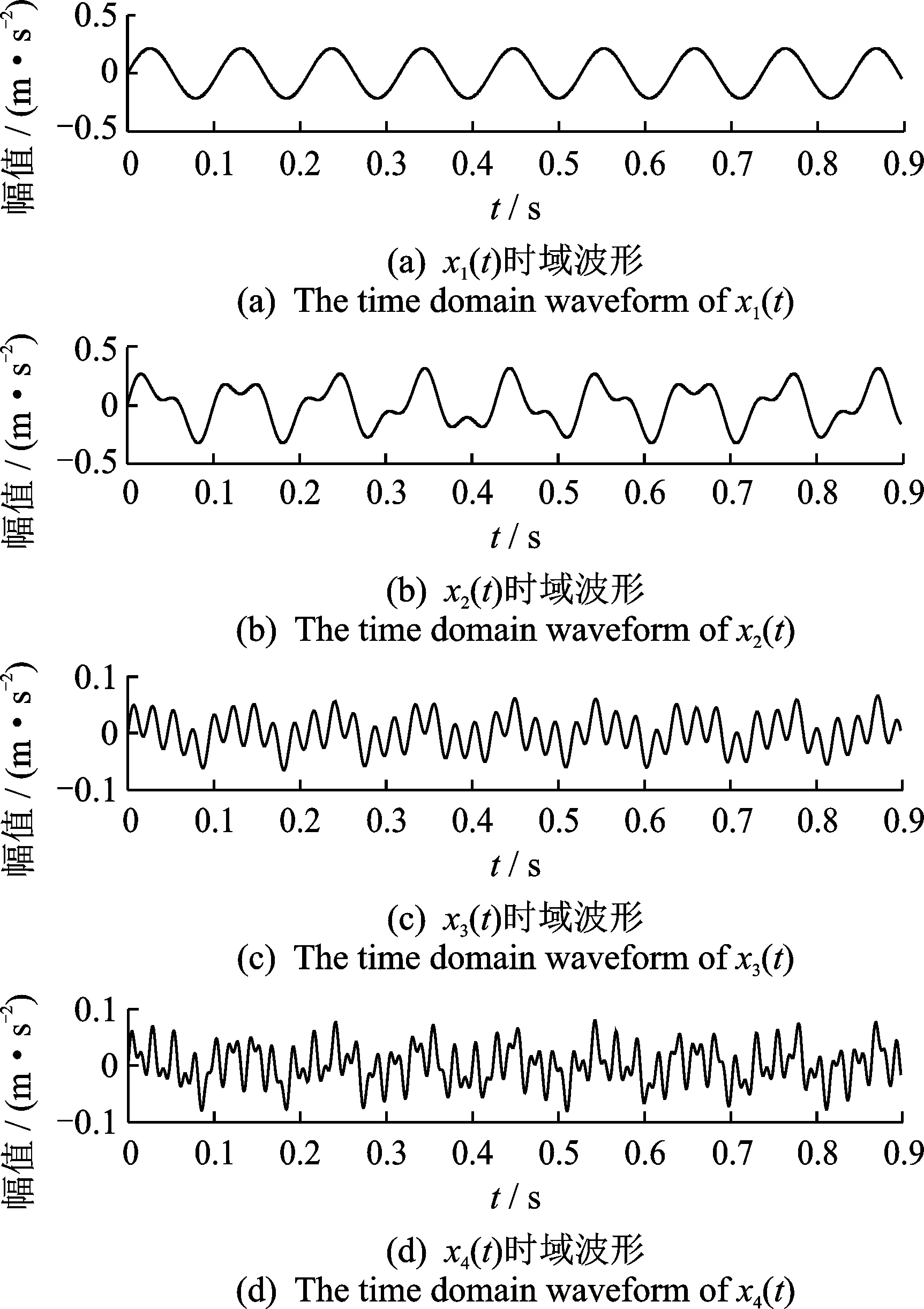
图3 仿真信号时域波形Fig.3 The time domain waveform of the simulation signal

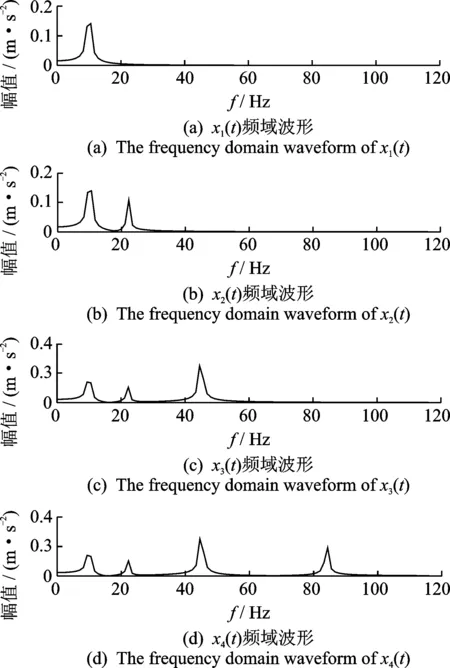
图4 仿真信号频域波形Fig.4 The frequency domain waveform of the simulation signal

下面分别计算上述信号的Lempel-Ziv指标，具体计算结果如表1所示。

表1 不同频率成分仿真信号的复杂度

Tab.1 The complexity of the simulation signal with different frequency components

信号x1(t)x2(t)x3(t)x4(t)复杂度0.006 50.013 00.059 90.063 8

由表1可以看出：随着信号频率成分的增加，Lempel-Ziv指标也随着增大，即Lempel-Ziv指标能够简单地有效地识别信号频率成分的增加。当轴承出现故障时，故障一般会存在一个由轻微到严重、由单一模式到复合模式的演化过程[22]。随着轴承出现不同程度的故障，轴承的振动信号中会逐渐出现分数倍或整数倍的谐波，频率成分随之而改变。因此，在单一故障模式下轴承不同程度的损伤可以使用Lempel-Ziv指标进行识别。

在实际环境中，噪声是很常见的干扰信号，为了将Lempel-Ziv指标能够应用于实际，需要考虑噪声对该指标的影响。噪声属于宽频带信号[23]，噪声会增大原始振动信号的频率成分，因此当振动信号中混有噪声时，Lempel-Ziv指标也会改变。

以信号x4(t)为例，添加噪声。构造信噪比分别为30，13，10，4 dB的信号及白噪声信号，信号的时域波形图如图5所示。

图5为不同信噪比下的时域波形，其中图5(a)为信噪比为30 dB的信号时域波形；图5(b)为信噪比为13 dB的信号时域波形；图5(c)为信噪比为10 dB的信号时域波形；图5(d)为信噪比为4 dB的信号时域波形；图5(e)为白噪声信号时域波形。

上述各个含有噪声信号的Lempel-Ziv指标的计算结果如表2所示。

表2 不同信噪比信号的复杂度

Tab.2 The complexity of the signal with different signal to noise ratio

信噪比/dB3013104白噪声复杂度0.072 90.269 50.363 30.610 61.000 0

通过表2可以明显的看出：随着振动信号中噪声成分的增加，相应的Lempel-Ziv指标也会增加。如果直接将Lempel-Ziv指标用于轴承损伤程度的识别，必然会导致损伤程度的识别结果出现偏差。因此，为了将Lempel-Ziv应用于实际问题，必须对振动信号进行消噪。

图5 不同信噪比下的仿真信号Fig.5 The simulation signals under different signal to noise ratio

下面针对不同信噪比下的x4(t)信号，利用50 Hz的低通滤波来模拟频率截断的消噪方式。分别计算50 Hz的低通滤波后的Lempel-Ziv指标与文中所提方法的Lempel-Ziv指标，并计算处理后Lempel-Ziv指标的降噪比与原始未加噪声Lempel-Ziv指标的误差比。计算结果如表3所示。

表3 降噪后不同信噪比信号的复杂度

Tab.3 The complexity of the signal with different signal to noise ratio after reducing noise

信噪比/dB低通滤波自相关复杂度降噪率/%误差率/%复杂度降噪率/%误差率/%300.052 040.1918.500.063 814.260130.055 9382.1112.380.067 7298.086.11100.053 3581.6116.460.063 8469.44040.055 9992.63112.380.074 2722.9116.30

由表3可以看出：低通滤波与文中方法均能消除信号中的噪声成分，但是与低通滤波消噪相比相关分析不仅有效消除信号中的噪声成分，还能最大程度的保留信号中的原始信息，还原信号原始的复杂程度。在噪声环境下，能更加精确的得到由单一故障所引起的信号复杂度。但是当噪声成分较大、信噪比较低时，信号的有用信息已淹没在噪声环境中，文中所提方法也会存在一个较大的误差率。

根据表1～3的计算和对比可以看出：噪声会增加Lempel-Ziv指标的估计误差，从而导致信号中有效频率成分的错误估计，使得信号在不同程度下的频率信息难以区分。在噪声环境下，与传统的Lempel-Ziv指标和滤波消噪后的Lempel-Ziv指标相比，文中所提方法能更有效区分不同的频率信息。

3.2 实验数据验证

下面用实验数据对文中方法进行验证。轴承内、外圈故障数据来自美国西储大学电气工程实验室[24]，型号为SKF6203，采样频率为4.8 kHz，损伤为用电火花加工而成的单点损伤，直径分别为0.177 8，0.355 6，0.533 4 mm，转速分别为1 750，1 730 r/min。

图6 故障轴承时频图Fig.6 The time-frequency diagram of fault bearing

由图6可以看出，故障轴承的能量主要集中在5 000 Hz以下，因此，分别计算实验数据在未处理、滤波降噪、自相关降噪后的解调谱，如图7所示。

由图7可见，图7(a)为噪声环境下轴承信号的解调谱；图7(b)为经滤波处理后轴承信号的解调谱，其中频率最高点的频率为152.5 Hz；图7(c)为经过自相关处理后轴承信号的解调谱，其中频率最高点的频率为161.9 Hz。

图7 不同预处理下故障轴承解调谱Fig.7 The demodulation spectrum of fault bearing under the different pretreatment

因此，由图7可以看出在噪声环境下，轴承故障的特征频率淹没在噪声的干扰下，并且滤波降噪也无法很好的消除噪声的干扰，而通过自相关降噪后可以很好的突出故障轴承的频率成分。

因此，将实验数据分别直接进行计算Lempel-Ziv指标、通过5 kHz低通滤波降噪后计算Lempel-Ziv指标和用文中方法进行计算，对轴承内外圈不同损伤程度数据进行上述方法计算后的结果及分析如下。

3.2.1 轴承内圈损伤程度识别

图8是内圈分别直接进行Lempel-Ziv指标计算(图8(a))、经过低通滤波处理后Lempel-Ziv值计算(图8(b))及经过相关处理后Lempel-Ziv值计算(图8(c))的结果。其中□为转速1 730 r/min下不同损伤程度的Lempel-Ziv复杂度值；△为转速1 750 r/min下不同损伤程度的Lempel-Ziv复杂度值。

通过图8(a)可以看出：随着磨损程度的增加，内圈单纯计算Lempel-Ziv指标表现出了先上升后下降的趋势。无法识别轴承不同的损伤程度。

图8 不同转速下内圈复杂度随磨损程度变化曲线Fig.8 The inner ring complexity with the change of the wear degree at different speed

通过图8(b)可以看出：随着磨损程度的增加，内圈滤波后的Lempel-Ziv指标表现出了先下降后上升的趋势。无法识别轴承不同的损伤程度。同时该方法下的Lempel-Ziv指标要明显小于其他处理方法下的值，说明经过低通滤波后，除了消除了部分噪声对于Lempel-Ziv指标的影响，同时也消除了一些由于轴承故障所引起的信息。

通过图8(c)可以看出：笔者所提改进算法计算后的内圈Lempel-Ziv指标随着磨损程度的增加逐渐减小，与内圈故障所表现出的信号特征相符。能有效用来区分内圈不同的损伤程度。同时Lempel-Ziv指标要明显小于单纯计算Lempel-Ziv指标的值；并大于滤波消噪后的Lempel-Ziv指标。说明经过自相关处理后不仅消除了信号中部分噪声对于Lempel-Ziv指标的影响，而且还能最大程度地保留轴承的故障信息。

通过图8中对不同处理方法后内圈的Lempel-Ziv指标对比可以看出，经过自相关处理后的Lempel-Ziv指标表现出明显的单调趋势，能有效识别轴承内圈不同的损伤程度，而其他方法则无法识别不同的损伤程度。因此，文中所提方法能有效用于轴承内圈损伤程度的识别。

3.2.2 轴承外圈损伤程度识别

图9 不同转速下外圈复杂度随磨损程度变化曲线Fig.9 The outer ring complexity with the change of the wear degree at different speed

图9是外圈分别直接进行Lempel-Ziv指标计算(图9(a))、经过低通滤波处理后Lempel-Ziv指标计算(图9(b))及经过相关处理后Lempel-Ziv指标计算(图9(c))的结果。其中□为转速1 730 r/min下不同损伤程度的Lempel-Ziv复杂度值；△为转速1 750 r/min下不同损伤程度的Lempel-Ziv复杂度值。

通过图9(a)可以看出：随着磨损程度的增加，外圈直接计算的Lempel-Ziv指标表现出了先上升后下降的趋势，无法识别轴承不同的损伤程度。

由图9(b)看出：在低转速下，通过低通滤波后的Lempel-Ziv指标表现出了上升趋势；而在稍高转速下Lempel-Ziv指标表现出了先下降后上升的变化趋势。说明故障轴承在不同转速下会出现不同形式的频谱。同时，该方法的Lempel-Ziv指标要明显小于其他处理方法下的值，说明经过低通滤波后，除了消除了部分噪声对于Lempel-Ziv指标的影响，同时也消除了一些由于轴承故障所引起的信息。

通过图9(c)可以看出：笔者所提改进算法计算后的外圈Lempel-Ziv指标随着磨损程度的增加逐渐增加，与外圈故障所表现出的信号特征相符。该方法可以识别外圈不同的损伤程度。并且Lempel-Ziv指标的大小要明显小于单纯计算Lempel-Ziv指标的值；并大于经过滤波消噪后的Lempel-Ziv指标。说明经过自相关处理后不仅消除了信号中的部分噪声对于Lempel-Ziv指标的影响，而且还能最大程度的保留轴承的故障信息。

通过图9中对不同处理方法后外圈的Lempel-Ziv指标对比可以看出，经过自相关处理后的Lempel-Ziv指标表现出明显的单调趋势，能有效识别轴承外圈不同的损伤程度。而其他方法则无法识别不同的损伤程度。因此，笔者所提方法能有效用于轴承外圈损伤程度的识别。

3.2.3 内外圈复杂度变化对比分析

下面对转速1 730 r/min时内、外圈不同损伤程度下的Lempel-Ziv指标进行对比分析。分别计算不同损伤程度下内、外圈Lempel-Ziv指标相对于第1个Lempel-Ziv指标的变化率。1 730 r/min时内、外圈的Lempel-Ziv指标变化率的值如表4所示。

表4 1 730 r/min下内、外圈复杂度变化率

Tab.4 The rate of the inner and outer rings complexity change under 1 730 r/min %

通过表4可以看出内圈Lempel-Ziv指标的变化率是负值，且随着损伤程度的加深，变化率绝对值也增加，说明内圈的Lempel-Ziv指标是逐渐减小的，这与内圈故障时所表现出的频率调制特征相符，即在单一故障模式下随着内圈故障程度的加深，内圈故障频率会逐渐与转频出现调制，频谱会越来越规律。所以，在单一故障模式下随着内圈故障程度的加深，内圈Lempel-Ziv指标会逐渐减小。

外圈复杂度的变化率正好与内圈复杂度的变化率相反。这一特征与外圈故障时表现出的幅值调制特征相符，即在单一故障模式下随着外圈故障程度的加深，外圈的频谱上会逐渐出现外圈特征频率不同倍数的谐波，频谱逐渐混乱。所以，在单一故障模式下随着外圈故障程度的加深，外圈的Lempel-Ziv指标会逐渐增加。

同时可以看出，在不同的磨损程度下，内、外圈Lempel-Ziv指标的变化率除在符号上的不同外，在数值上相差并不大。

通过仿真数据的计算可以看出，Lempel-Ziv指标能很好地识别信号中频率成分的变化。但是当信号中含有噪声时，Lempel-Ziv指标会受噪声的影响而失去准确性。笔者提出的改进算法能有效消除噪声对于Lempel-Ziv指标的影响，并能最大程度地保留轴承的故障信息，得到较准确的故障信号复杂度。通过实际轴承数据可以看出笔者所提出的算法在单一故障模式下能有效识别出轴承不同的损伤程度。

4 结束语

仿真数据及实验数据的分析结果表明，自相关分析能在保留轴承全部故障信息的前提下有效消除信号中的噪声成分，减小噪声对于Lempel-Ziv指标的影响。使得Lempel-Ziv指标能够精确的反映信号频率的复杂程度。在实际中采集得到的信号往往会含有噪声成分，笔者给出了一种在噪声环境下，识别轴承单一故障模式下不同损伤程度的方法。通过轴承实际数据验证了所提方法的有效性。具体表现在：当内圈损伤程度逐渐加重时，Lempel-Ziv指标逐渐减小；当外圈损伤程度逐渐加重时，Lempel-Ziv指标逐渐增加。