柔体动力学模型的机器人关节振动分析与抑制*
2019-05-09覃彬彬刘晓刚
张 铁, 覃彬彬, 刘晓刚
(1.华南理工大学机械与汽车工程学院 广州,510641) (2. 桂林航天工业学院广西高校机器人与焊接重点实验室 桂林,541004)
引 言
垂直六自由度工业机器人的关节采用RV减速器及具有柔性较大的同步传动带系统驱动关节运动时,关节和连杆的柔性效应的增加,使得结构发生变形与共振,导致任务的期望精度降低。尤其近年来对装配精度要求更高的3C电子行业中,机器人广泛应用在高速分拣零部件过程中手臂惯性力使得关节弹性形变更为明显,造成的机械谐振不仅影响伺服系统的稳定性与跟踪精度,还会损害机械部件,降低其寿命。因此如何抑制机械谐振频率、实现振动抑制受到当今国内外专家学者的关注。
文献[1]采用设计控制器的方法,利用速度环反馈控制方式抑制了伺服系统的谐振。文献[2]针对载体位置不受控、姿态受控的情况,提出了柔性空间机械臂振动抑制的模糊终端滑模控制方案,运用奇异摄动法将系统分解为慢变、快变两个子系统并分别设计了控制器实现柔性臂的振动抑制。文献[3]根据模型不确定性和外界扰动因素,利用反演法与干扰观测器相结合的控制方法实现对两惯量系统的振动抑制。文献[4]针对柔性并联机器人的结构振动及控制问题,采用比例-微分(proportional-derivative,简称PD)反馈控制器和电感自谐振频率(self-resonant frequency,简称SRF)应变率反馈控制器相结合的混合控制方法来进行轨迹跟踪与振动抑制。文献[5]在传统比例-积分(proportional-integral,简称PI)控制结构的基础上应用低通滤波器、常用陷波器和双T型陷波滤波器,然后比较了3种滤波器抑制伺服机械谐振的效果并指出双T型陷波滤波器性能较优。Wang等[6]提出了一种具有振动频率自动搜索功能的自适应陷波器,降低了永磁同步电机线性反馈系统的机械振动。
针对机器人伺服系统中的柔性传动环节导致的机械谐振问题,笔者研究基于柔体动力学模型的机器人振动抑制的解决方法。该方法包括建模、模态分析、仿真和实验。通过对机器人第5关节(J5轴)建立柔体动力学模型,从理论上分析其产生振动的原因,结合有限元软件ABAQUS强大的非线性分析功能,深入说明其变形的因素;基于ABAQUS优化测点的力锤激励法对J5轴进行模态频率的提取;获得谐振频率后采用双T型陷波滤波器进行设计,通过仿真比较,得出最优的设计参数值。
1 柔体动力学数学模型建立
目前,负载在1 000 N以下的六自由度工业机器人常采用电伺服驱动系统,关节的机械传动部分包括传动轴、联轴器、减速器等,由于这些传动机构存在一定的弹性,使得机械系统本身产生振动。
如图1所示,由于机器人各个关节均采用了电机和减速器的结构形式,且由于电机转速频繁变化,当电机驱动频率接近谐振频率时,关节将产生机械共振,而其中第5,6关节采用的是电机通过同步带和减速器传递运动,其谐振频率较低。笔者将仅对J5轴的振动展开研究,其他轴的共振和抑制方法类似。

图1 六自由度工业机器人Fig.1 Six-degree industrial robot
J5轴的结构如图2所示,其驱动系统柔性因素有:同步带、同步带轮和谐波减速器,为分析简便,结合弹簧的柔性特点,文献[7]将这些柔性因素等价于弹簧质量系统,得到图3所示的电机-弹簧-质量的两惯量系统。

图2 J5轴模型图Fig.2 J5 axis model
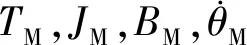

图3 电机-弹簧-质量的两惯量系统Fig.3 Two inertia systems of motor-spring-mass
根据力平衡原理,分析此两惯量系统有
柔性轴传动部分
TS=KS(θM-θL)
(3)

由式(1)~(3)并经拉普拉斯变换后,得到系统的传递函数如图4所示。

图4 两惯量模型的结构图Fig.4 Structure diagram of two inertia model
因此,电机转速和电机力矩之间的传递函数Q(s)为
(4)

由式(4)可知,机器人关节柔性系统中存在着零、极点,导致伺服系统的振动。根据笔者所研究的机器人,式中初始参数JM=0.277×10-4kg/m2,JL=0.1×10-4kg/m2,BM=0.05,BL=0.01,KS=60,可得系统伯德示意图如图5所示。

图5 系统伯德图Fig.5 System bode diagram
由图5可知,两惯量系统中存在谐振频率点a和反谐振频率点b。这些谐振频率点制约着系统响应带宽的提高,必须对其进行调节或抑制。
2 陷波滤波器
机器人J5轴两惯量系统存在谐振点和反谐振点的问题可以从控制器中设计陷波滤波器来对其抑制[8]。J5轴的交流伺服系统采用速度环、电流环双闭环控制,串联陷波滤波器后的系统框图如图6所示。将陷波滤波器串入速度环控制回路中,对速度控制器输出的电流环给定信号进行陷波滤波,抑制电机电流的振荡,进而对电机输出电磁力矩产生抑制,最终达到抑制机械谐振的目的。

图6 串联陷波滤波器结构图Fig.6 Series notch filter structure graph
对于一般的二阶惯量系统有两个极点、两个零点,常用陷波滤波器[9]传递函数,其形式为
(5)
其中:ω0为陷波频率;K为可调参数,用于改变带宽。
上述的陷波滤波器形式只能确定陷波频率点和对称调整带宽,而不能调整陷波器衰减的幅值和形状。
为了减小谐振点处幅频特性曲线上的幅值裕量(如图5中的a点幅值或b点幅值),达到消除共振的目的,采用双T型陷波滤波器[10-12],对陷波深度进行调节,使得陷波深度接近谐振频率点的幅值裕量,避免系统因陷波深度过大或者过小而导致不稳定,其传递函数为
H(s)=(as2+cs+1)/(as2+bs+1)
(6)
其中:ω0为陷波频率;k1为陷波带宽参数;k2为陷波深度参数。
这3个变量可决定滤波器的系数a,b,c。
陷波带宽Bω以及陷波深度Dp与系数k1和k2之间的关系为
(7)
通过调节陷波频率ω0改变陷波滤波器的零点,抵消系统的谐振极点以及调节陷波带宽系数k1实现附加极点位置的调整。在设计滤波器参数时,应先确定系统的谐振频率ω0,再根据谐振频率确定其陷波带宽参数k1和陷波深度参数k2。
由于系统谐振频率未知,而设计速度环中的陷波滤波器需要谐振频率、振型、阻尼比等未知参数,所以机器人的J5轴将采用有限元分析法、力锤激励法分别对其模态参数进行识别。
3 结构动力学模态分析
利用有限元分析软件ABAQUS对机器人J5轴进行模态分析,获取低阶主导模态的信息,为力锤激励法激励点的选取提供优化方案,分析流程主要有前处理、计算阶段和后处理三部分。为节省计算时间,在不影响结果准确性的前提下,对于J5轴的前处理工作[13]主要通过Solidworks建立三维模型,将其导入ABAQUS中进行分析,J5轴各个零件的材料力学性能参数如表1所示。

表1 材料力学性能参数表
对于轴,压盖和负载选用ABAQUS中网格划分单元类型中的C3D8R单元,其余的不规则部件都采用C3D4单元类型进行网格划分。定义接触面摩擦因数信息以及装配信息,如轴承由轴承座固定在基座上等;定义零部件的边界条件,如所有螺栓孔、轴承座外圈的绑定约束,约束其六个自由度,对于同步带轮、轴承内圈等只释放z,x自由度,约束其余自由度。
完成前处理后,设定线性频率提取分析步进行后处理,收集分析运算结果,直接提取有效数据。图7为经ABAQUS的分析步计算,得出J5轴的低阶振型图。

图7 模态分析图Fig.7 Modal analysis diagram
由图7(a)可知,J5轴的一阶模态主要变化是同步带绕y轴的扭转变形;图7(b)二阶模态主要变化是从动轮与同步带绕y轴的变形,激励点选择作为模态实验的重要组成部分,不仅决定着能否激发出所有关注的模态,而且还关系到影响数据的精度,利用基于ABAQUS测点优化方法[14],根据图7(b)的二阶模态振型的同步轮扭曲处布置激励点,实验选取的激励点如图8所示。

图8 激励点与测试点分布Fig.8 The placement of exciting and measured points
力锤激励方法的测试系统包括电脑、亿恒AVANT数据采集与分析仪、模态分析软件、力锤及三向加速度传感器等。
在被测物体上安装加速度传感器用来接收响应信号,可以测得输入和输出信号,最后通过亿恒科技的AVANT数据采集与分析系统对这两路信号进行处理,结合Model Genius2.0模态分析软件进行模态分析,获得如图9所示的模态参数结果。
结构动力学模态法获取得到的谐振频率结果整理如表2所示,为设计陷波滤波器的陷波频率等提供依据。

图9 J5轴的模态实验结果Fig.9 Modal experiment results of J5 axis
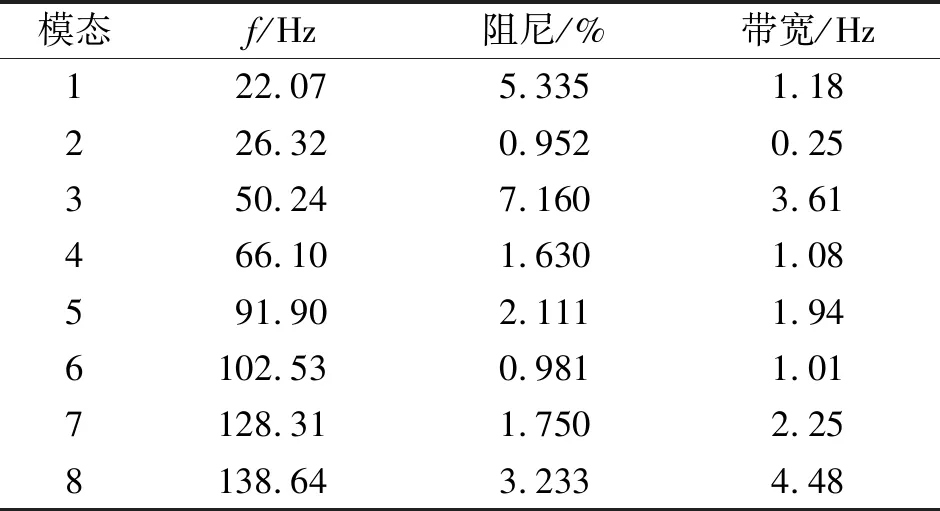
模态f/Hz阻尼/%带宽/Hz122.075.3351.18226.320.9520.25350.247.1603.61466.101.6301.08591.902.1111.946102.530.9811.017128.311.7502.258138.643.2334.48
4 仿真与实验
设计常用陷波滤波器时,取J5轴陷波频率66.1 Hz。为了分析K值对于陷波衰减深度的影响,根据仿真,逐渐调节式(5)的K,若先定义K=0.2,递减时任取数值如0.02;递增时任取数值如0.6,通过Matlab仿真得到式(5)所描述的陷波器伯德图(见图10)。

图10 常用陷波器伯德图Fig.10 Bode diagram of notch filter
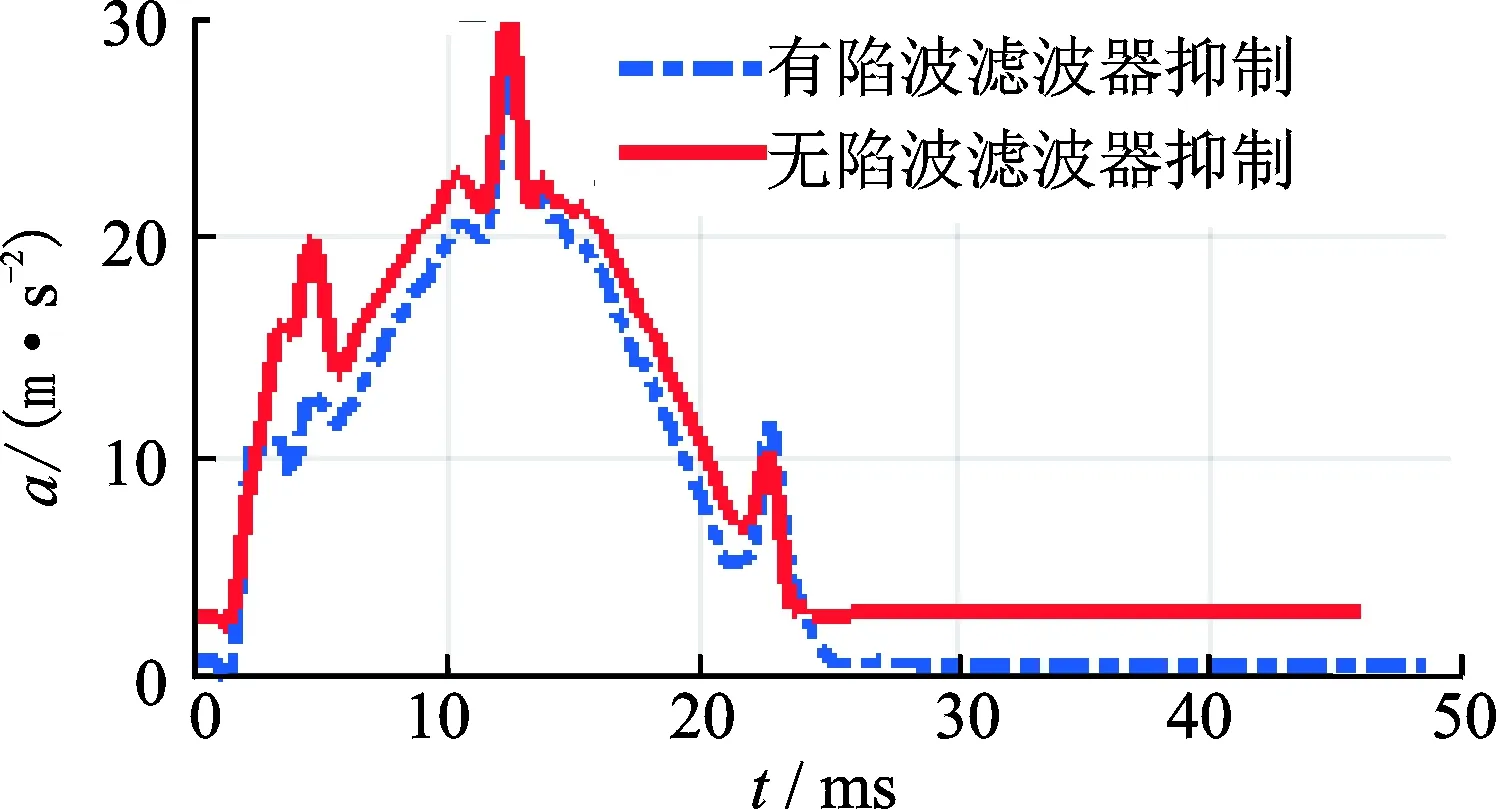
在图10陷波器幅频特性曲线中,K任取梯度性的3个值,都使得谐振点幅值处于200 dB以上,通过仿真得知常用陷波器形式只能确定陷波频率点,而不能调整陷波器的的陷波深度。为了能调整陷波器的衰减深度,满足伺服驱动器设置陷波深度参数0~32 dB的范围要求,采用双T型陷波滤波器设计方案,涉及到的计算变量有:表2中的J5轴谐振频率ω0为66.10 Hz,带宽Bω为1.08,阻尼比为1.630,从而由式(7)可确定k1=0.016,取k2 图11 双T型陷波器作用系统伯德图Fig.11 Bode of double T notch filter action system 由图11幅频特性曲线可见,系统谐振点与陷波器凹陷点的峰值相抵消,幅值下降为0;相位角趋近于0。采用双T型陷波滤波器能有效避免谐振点附近其他频率信号的相角出现滞后(超前)现象,降低相频特性的恶化,稳定了伺服驱动系统。 为了验证双T型陷波滤波器对机器人振动抑制效果的有效性,以广州数控六自由度工业机器人J5轴为例进行振动抑制实验。 如图12所示,该平台的控制算法以研华510工业控制计算机为核心,采用C语言编程实现,人机交互界面由C#编程建立。控制系统是Windows实时中断内核的PC运动控制系统,工控机通过EtherCAT总线将控制量发送到伺服单元,系统控制周期为1 ms。控制回路采用德国倍福公司的模拟量输入模块,传感器采用的是德国KISTLER公司的三向加速度传感器,输出电压为±60 mV,测量范围为±30 g,J5轴的交流伺服驱动器额定功率为400 W,额定转速3 000 r/min。设置伺服驱动参数陷波频率66.1 Hz以及陷波深度20 dB。系统给定信号为5个周期0→2 000 r/min的正反向阶跃信号,在规定的运动轨迹中,分别在有无陷波滤波器的条件下采集加速度信号量并进行数据处理,比较余振对末端各方向加速度数值变化的影响,得到加速度分析图如图13~15所示。 图12 机器人实验平台Fig.12 Robot experimental platform 图13 总加速度分析图Fig.13 Acceleration analysis diagram 图14 z方向加速度分析图Fig.14 z direction acceleration analysis chart 图15 y方向加速度分析图Fig.15 y direction acceleration analysis chart 由图13可知,陷波滤波器抑制的总加速度比没有的降低28.5%。图14中加了陷波器补偿后,z方向上振幅的加速度值能在3 s内由原先的最大加速度3下降为0.5 m/s2,图15的y方向上振幅的加速度值由原先无陷波补偿的绝对值0.2 m/s2降为0。 从末端加速度分析图中可明显看出陷波滤波器的作用效果,说明设计时仿真的陷波深度满足了当前谐振频率的陷波器设计要求。谐振频率被陷波滤波器滤掉,如图11所示的谐振频率的谐振点峰值被削减至零。 采用噪声量化手段对J5轴进行振动抑制的噪声分析,检测工具采用希玛仪表的数字式声级计AR844,测量位置距离机器人底座中心距离约55 cm,1 s实时对J5轴进行噪声监测,得到无陷波滤波器作用的噪声量级71降至65.9 dB,噪声量级降低了约5 dB,体现了陷波滤波器良好的干扰抑制特性。 图16分析电机停止起读取的编码器值,由于余振导致电机转角编码器数值变化明显,将编码器值进行数据处理后,在陷波器补偿下,电机转子偏移量绝对值从1°降至0.5°。图17所示的运动阶段加了陷波补偿的末端加速度值降低约20%,最终降至0,体现陷波滤波器有良好的振动抑制效果。 图16 电机转子偏移量Fig.16 Motor rotor offset 图17 运动阶段末端加速度分析图Fig.17 Analysis diagram of motion end acceleration 针对高速运动机器人由于柔性因素所引发的机械谐振问题,提出了基于柔体动力学模型的机器人关节振动抑制的解决方法。该方法通过建模、模态分析、仿真及实验四个方面对广州数控机器人第5关节展开了研究,以J5轴振动产生的因素为研究对象,结合有限元及力锤激励法实现了对机器人手臂的谐振频率的获取,采用双T型陷波滤波器设计算法进行仿真比较,得到最佳参数,克服了传统常用陷波器的设计方法的局限性,解决了机器人J5轴的振动问题。陷波实验结果表明末端Z方向上振动幅值最大,其余振幅值加速度从3降为0.5 m/s2,最后趋于0,电机转子偏移绝对值从1°降至0.5°。该方法可应用机器人关节轴的振动抑制,具有一定的工程实用性。





5 结束语
