广义指数分布族参数的经验Bayes检验问题

黄金超

（滁州职业技术学院 基础部，安徽 滁州 239000）

0 引言

指数分布族参数的经验Bayes检验问题已有很多研究,如文献[1-5]对其做了不同程度的统计推断研究,并获得一些重要有意义的结果。彭家龙等[6]研究了Cox模型参数的经验Bayes检验，在适当的条件下，收敛速度的阶可任意接近但绝大多数研究经验Bayes检验问题的文献，都是利用密度函数的通常核估计来构造核函数。本文将采用密度函数的递归核估计和EB检验函数的单调性，重新构造一类广义指数分布族参数的检验函数。在一定的条件下获得了收敛速度的阶可任意接近O(n-1)。改进了文献[6]的EB检验相应结果，推广了现有文献的相应结果。

考虑如下广义指数分布族[6]：设：

这里 q(x)和 Q(x)为连续q(x)=Q′(x)＞0， Q(x)＞0,且参数空间为

考虑分布族式（1）中参数θ的如下EB检验问题

其中，θ0＞0为已知常数。

对检验函数式（2）,设损失函数为“线性损失”。

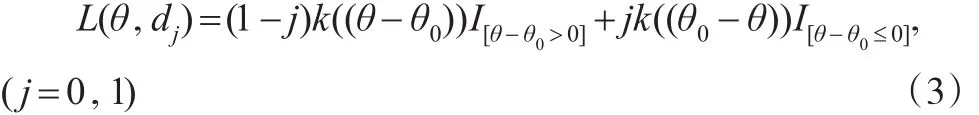
设k＞0且为常数,D={d0，d1}是行动空间,d0表示接受H0,d1表示否定H0,I[A]表示A的示性函数。

设G(θ)为θ未知先验分布，且：

式（4）为随机化判别函数,则δ(x)的风险函数为：

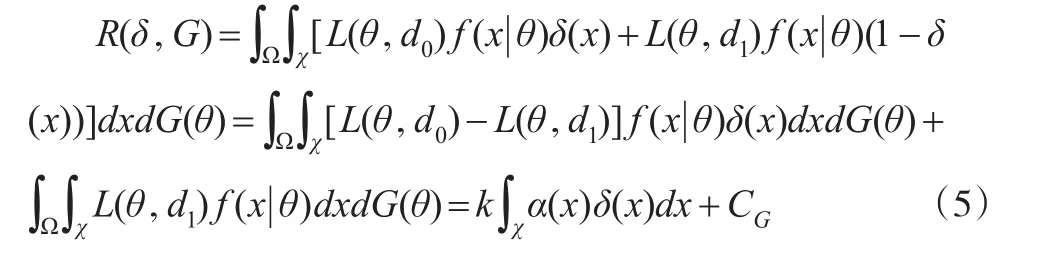
此处：

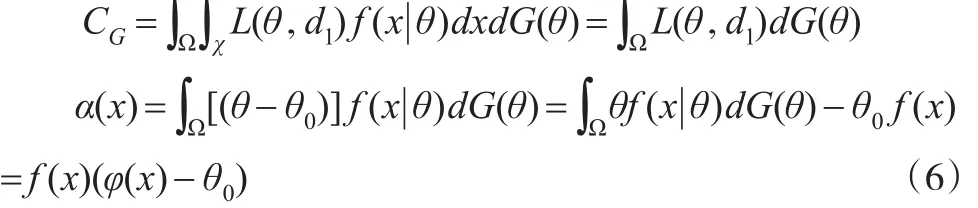
其中：

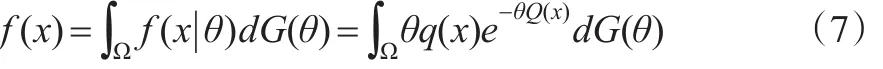
为r.v.X的边缘分布,而：

由式（6）至式（8）得α(x)的另一表达式：

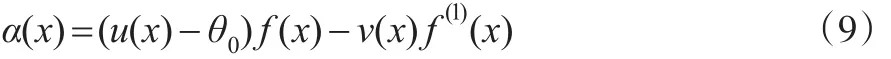
其中，f(1)(x)、q(1)(x)分别为f(x)、q(x)一阶导数，u(x)

由Cauchy-Schwarz不等式和式（8）可得：

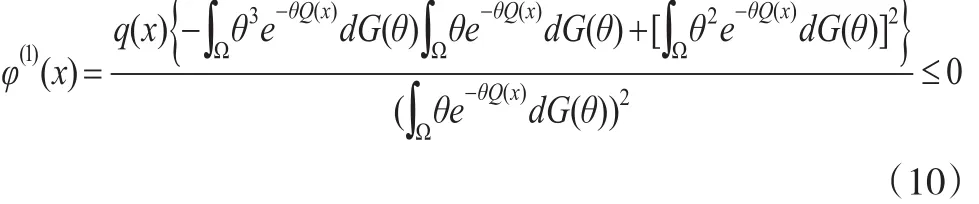
其中，φ(1)(x)为φ(x)一阶导数,由式（10）可知φ(x)是单调递减且连续。

本文假定：

在假定式（11）成立下，先验分布G(θ)是非退化的,由介值定理可知，一定存在点aG∈(0，∞),使得φ(aG)=θ0。又由式（9）可知：

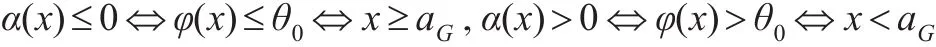
因此，由式（5）可知Bayes判决函数为：

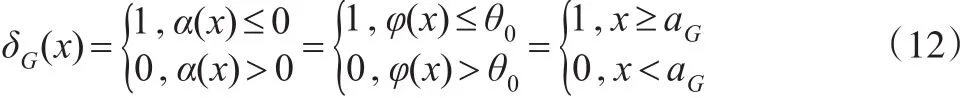
其Bayes风险为：

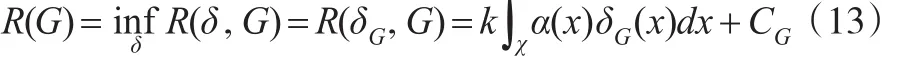
在式（13）中,当先验分布G(θ)已知,且δ(x)=δG(x)时，R(G)可以达到的,但此处G(θ)未知,因此δG(x)无使用价值,于是引入EB方法。

1 EB检验函数的构造

设X1，X2，…，Xn和X是iid样本,令密度函数为f(x)如式（7）,iid样本作如下假定:

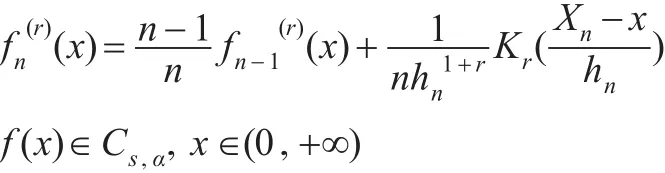
假定Cs，α表示R1中一族密度函数,其s阶导数存在,的正整数。

令Kr(x)(r=0，1，…，s-1)是有界的Borel可测,在区间（0,1）之外为0,且满足（B）：

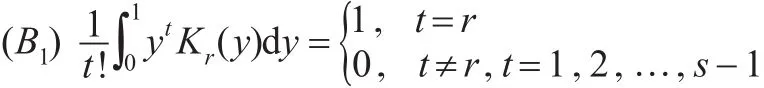
(B2)Kr(x)在R1上是可微的，且

本文假定先验分布G(θ)非退化,且属于下列先验分布类：

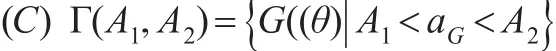
这里A1、A2为给定的常数,0＜A1＜A2＜∞,通常取A1为充分小A2充分大。

记f(0)(x)=f(x),f(r)(x)为f(x)的第r阶导数，r=0，1，…,s。定义f(r)(x)的递归核估计[7]为：

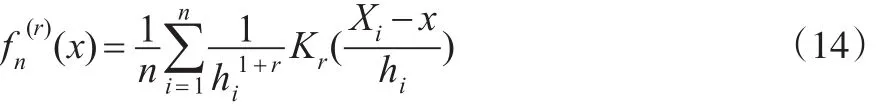
其中，hn↓0且hn＞0,Kr(x)是满足条件(B)的核函数,此估计具有一种递归性质,即：

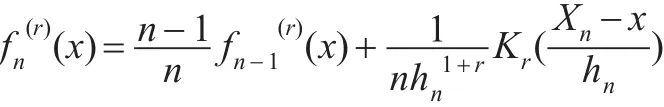
定义α(x)的估计量：

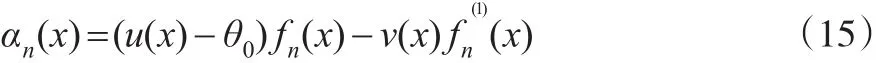
由假设(C)，结合式（12），定义EB检验函数为：

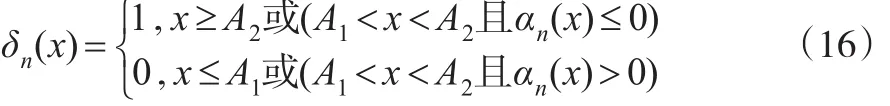
EB检验的构造方法由文献[8]最先提出来的。

令En表示对 r.v.X1，X2，…，Xn的联合分布求均值,则δn(x)的全面Bayes风险为：

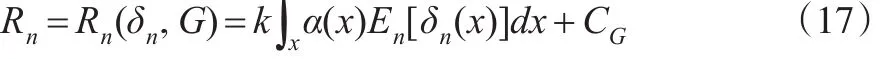
假定c0，c1，c2，…表示与n无关的正常数：

引理 1：设fn(r)(x) 由式（14）定义,其中X1，X2，…,Xn为 iid样本序列,假定条件（A）和（B）成立,hn↓0,当时,则有：

证明：由Cr不等式可知,对r=0,1有：

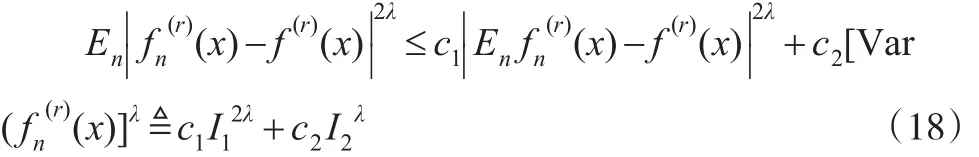
由式（14）和核函数的性质可知：

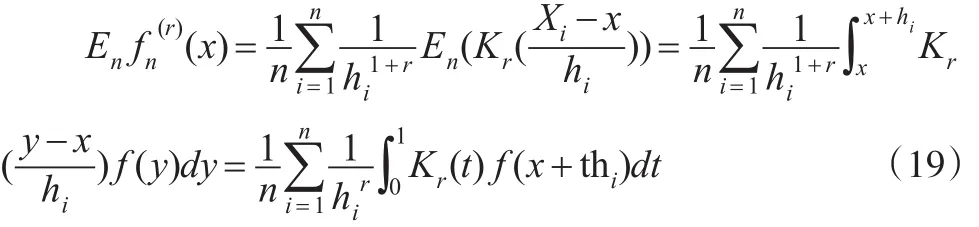
由Taylor展开得：

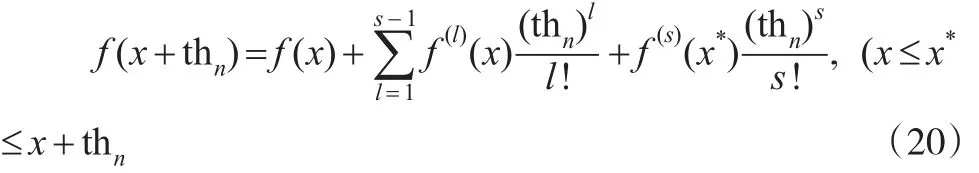
将式（20）代入式（19）可得：

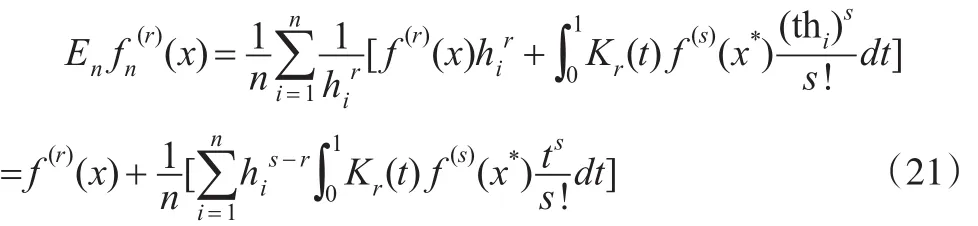
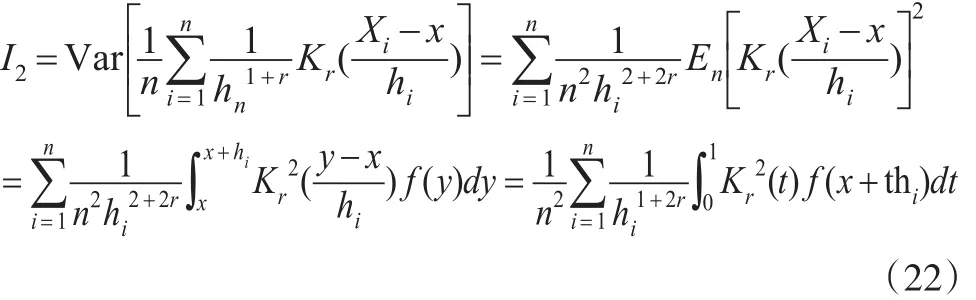
再由f(x)∈Cs，α， 及|Kr(t)| ≤C,X1，X2，…，Xn单调递减可知：

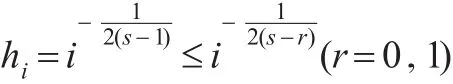
由式（22）可得：

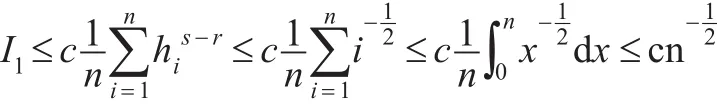
故有：

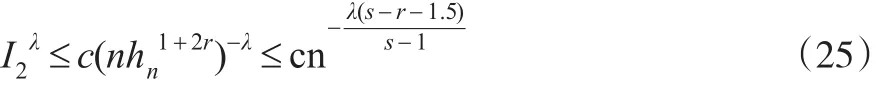
将式（24）和式（25）代入式（18），结论成立。

注1：当 0＜λ≤1时可任意接近Rn-R(G)。

2 EB检验函数的主要结果

定理1：设X1，X2，…，Xn为来自分布族（1）iid样本序列。R(G)、Rn分别由式（13）和式（17）给出，且假设（A）—（C）成立,当时，有：

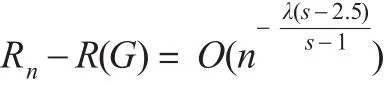
这里s≥3的正整数。

证明：由式（13）和式（17）可知：

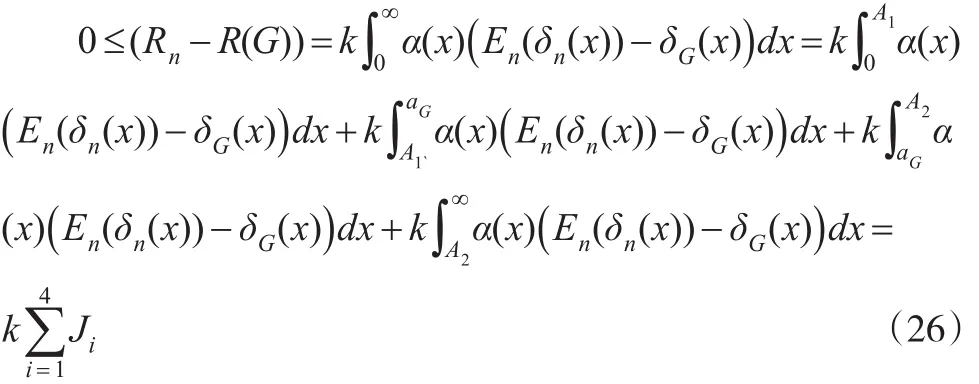
由式（9）和式（15），Cr不等式与引理1可知：

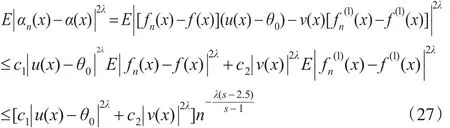
当x∈(0，A1)时,由式（12）和式（16）可知,δn(x)=0，δG(x)=0,x∈(A2，∞)时,δn(x)=1，δG(x)=1。 故En(δn(x))-δG(x)=0,因此：

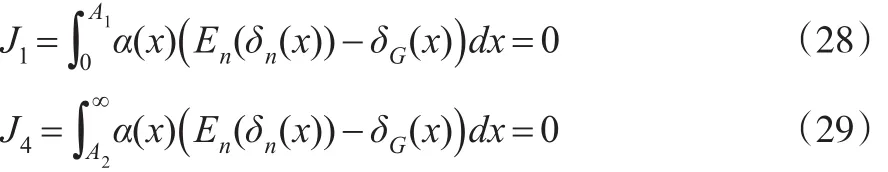
当x∈(A1，aG)时，由式（12）和式（16）可知，δG(x)=0，,利用Markov不等式和式（27）有：

当12＜λ＜1时,且是 第 2 类 瑕 积 分, 瑕 点 为x=aG,由式（8）、式（10）和比较判别法则：

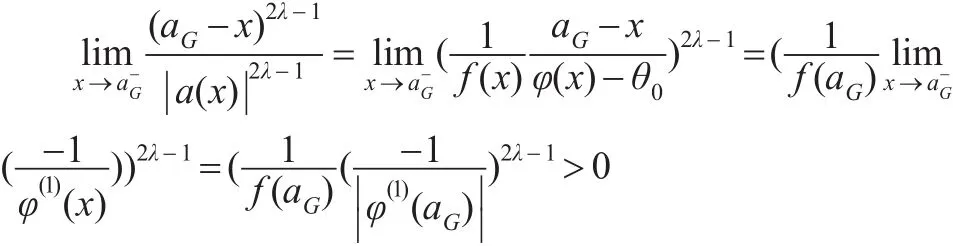
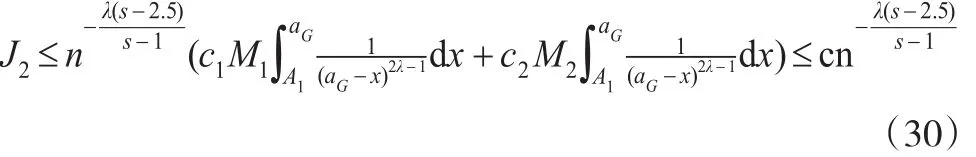
同理可证：

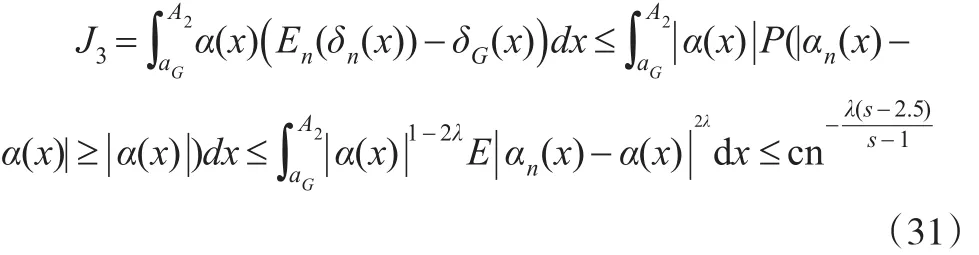
因此，将式（28）至式（31）代入式（26），得：

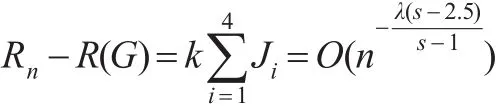
注2：文献[6]在舍入数据下构造的经验Bayes检验,得到了收敛速度阶为,其中 0＜λ＜1,s≥4,当λ→1，s→∞时,可任意接近。本文利用递归核估计和EB检验的单调性，重新建立EB检验,得到收敛速度的阶为。其中 0＜λ＜1,s≥3,当λ→1，s→∞ 时可任意接近于O(n-1)。文献[6]在舍入数据下的条件,构造EB检验比本文复杂；文献[6]定理的条件要求s≥4比本文s≥3要强,本文引理的证明比文献[6]引理1要简单些。由于本文利用EB检验的单调性,在一定的条件下，获得了收敛速度的阶的结果比文献[6]快了约1倍,改进文献[6]中的相应结果。

3 例子

在式（1）中，设Q(x)=x2则r.v.X为Rayleigh分布，即f(x|θ)=2xθe-θx2I(x＞0)， 设θ的先验分布族为：

β和r为常数且β＞0，r＞0，有

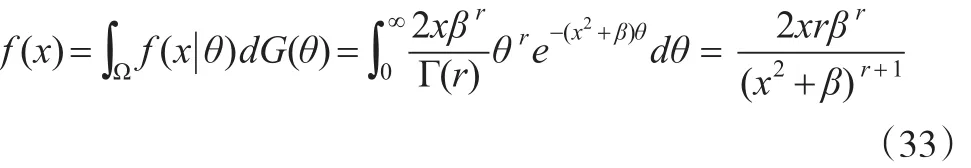
由式（33）可知f(x)关于x任意阶可导函数且有界,即f(x)∈Cs，α,条件（A）成立,在假定（B）成立,故验证（C）成立即可。

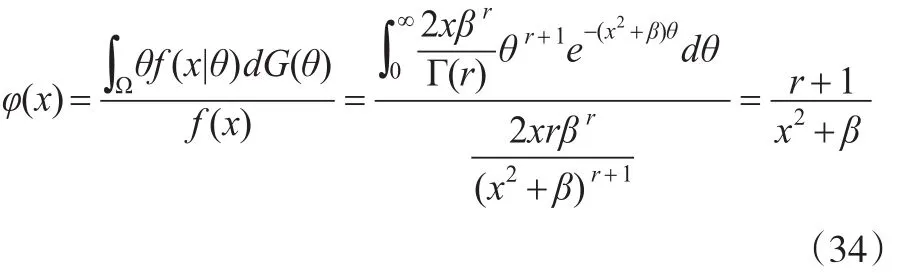
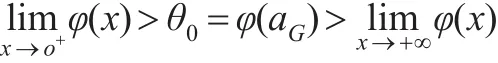
即假定（C）也成立,故定理1成立。