基于建筑专业的中职数学教学的整合研究

黄锋

摘要：本教学案例是中职数学与建筑专业进行整合的一次尝试，是以建筑专业为基础，对原教材进行适度整理，在确保知识结构不变的前提下，精心改编了一系列与建筑专业有关联的数学问题。本案例意图通过创设问题情境，由问题作为导向，让学生在教师的引导下，通过自己的主动参与，寻找解决问题的途径和方法，拓展学生的思维;通过问题的解决和反思，让学生自主归纳解决线性规划问题的基本步骤和方法，理清基本的數学知识和解题思路，让学生感受到学好数学的成功感。通过参与知识的呈现过程，真正实现数学学习与建筑专业的有机整合。

关键词：线性规划;图解法;整合研究

中图分类号：G712文献标识码：A文章编号：1992-7711（2019）05-031-2

一、基本情况

1.授课对象

本次授课的对象为建筑工程技术专业二年级学生，学生数学基础一般，学习能力差别大。

2.教材分析

本次授课所用的教材为《数学》（江苏省职业学校文化课教材），“线性规划的图解法”为第十八章第2节内容，本节内容分为两课时，本次授课为第一课时。通过对原数学教材进行适度整理，精心设计了一系列与建筑专业有关联的数学问题，通过问题引导，让学生体会到数学与专业的有机整合，同时可以培养学生分析、解决实际生活问题的能力，从而提升课堂教学效果。

根据以上认识，笔者确定本次课的教学目标如下：

（1）通过问题设置来理解线性规划问题的三要素，能把与专业相关的实际问题转化成数学中的线性规划问题，并能利用图解法解决这些实际问题;

（2）通过对与建筑专业相联系的实际问题的建模，培养学生观察、分析、联想以及作图的能力，提高学生“建模”和解决实际问题的能力，通过与专业相关的例题讲解，培养学生的专业意识;

（3）培养学生“想学数学”的积极性和“会用数学”的意识，提升学生解决问题的能力;鼓励学生树立创新意识，培养团结协作精神。

本次课的教学重点是把与建筑专业相关联的实际问题转化成线性规划问题，即数学建模，然后利用图解法给出相应解答。教学难点是数学模型的建立，即如何把实际问题转化为线性规划问题，再利用图解法解决线性规划问题。

本次课的教学，通过专业问题的引领，体现了“数学知识为辅，专业问题为主”的教学理念，以多媒体等信息化演示为基础，以“问题引领”为主导，通过一系列问题的设置，创设学习环境，通过互动交流，让学生经历知识的转变、提升、归纳、升华的全过程，实现数学学习与建筑专业的有机整合。

二、教学过程

1.新课导入，激发兴趣

在了解了线性规划的概念的基础上，今天，我们就以所学的建筑专业为背景，来研究一下线性规划在我们建筑专业中的应用。

（教师在学习平台上先播放一段某市城东新区建设规划的视频）

设计意图：通过信息化的直观展示吸引学生，激发学习兴趣;同时要让学生产生这样的疑问，本节课与我们所学的建筑专业又会有怎样的联系呢？

2.旧知回顾，提出问题

问题1：线性规划的概念，能否例举现实生活（建筑专业）中的规划问题？

设计意图：让学生联系生活实际，例举与专业相关的典型案例，激发学生学习的兴趣。

问题2：线性规划解题的基本步骤有哪些？关键在哪里？

设计意图：通过回顾线性规划的概念和解法，结合生活实际，让学生自己归纳两者的联系，使学生产生运用数学知识解决实际生活问题的初步设想。

3.引入例题，理解新知

例1：我市某建筑公司在城东某地块欲开发居民小区，若造一栋普通的多层住宅楼，需投入资金300万元，并占地200平米，可获利润70万元;若造一栋别墅需投入资金200万元，并占地300平米，可获利润60万元。该公司现有资金9000万元，拍得土地11000平米，请问应作怎样的投资方案，该建筑公司才能获利最多？

解析：设建造普通住宅楼x栋，建造别墅y栋，获利为z万元

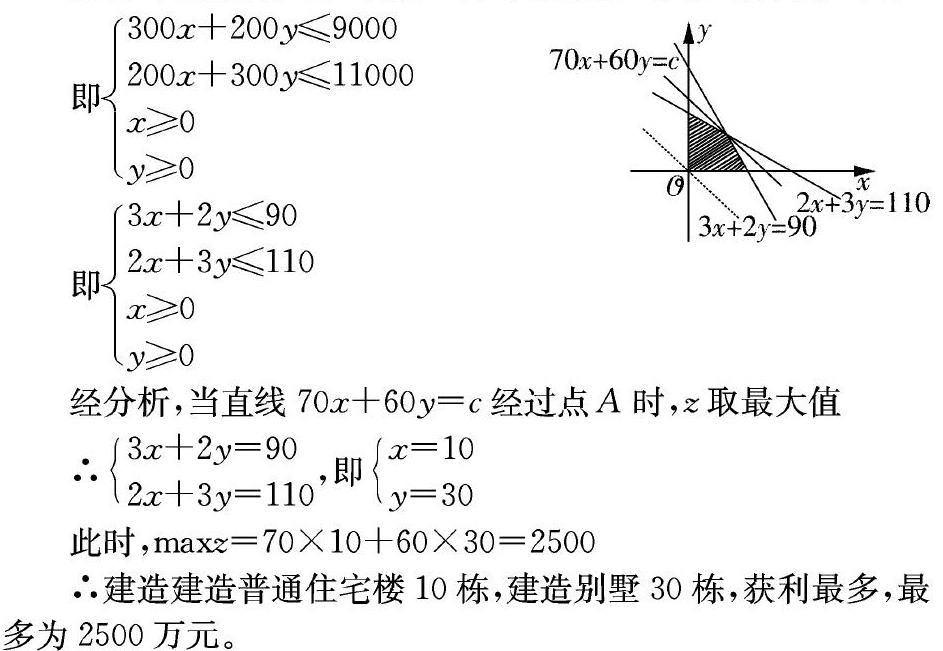
即300x+200y≤9000200x+300y≤11000x≥0y≥0

即3x+2y≤902x+3y≤110x≥0y≥0

经分析，当直线70x+60y=c经过点A时，z取最大值

∴3x+2y=902x+3y=110，即x=10y=30

此时，maxz=70×10+60×30=2500

∴建造建造普通住宅楼10栋，建造别墅30栋，获利最多，最多为2500万元。

评注：利用线性规划解决实际问题的主要步骤如下：

（1）审题：仔细阅读题目，抓住关键，理清题意，要分清哪些是限制条件，哪些是主要变量。由于线性规划应用题中的量较多，为了进一步理解题目中量与量之间的关系，可以借助图形或表格;

（2）设元：设题目中起重要作用的（或联系较多的）量为未知量x，y，并列出相关的不等式组和目标函数;

（3）作图：作图要准确，通过平移的方法来找点（最优解）;

（4）求解：将求出的点代入目标函数来求出最值（最大值或最小值）;

（5）检验：根据结果，检验反馈。

设计意图：新概念的运用或者是在新的问题环境中遇到相同的概念，其实质就是对概念的一次形象化具体化的理解，都会让学生加深对概念的理解。因此，要使学生对概念有更深刻地理解，最理想的方法就是运用概念解决实际问题，学生通过亲身体验，自我归纳，发现规律，掌握解题步骤，才能真正理解并掌握概念。通过这样的教学模式，才能真正实现数学学习与建筑专业的有机整合。

例2：一工程队要装修某住宅小区中的一批新房，已知装修一套别墅，木工需360小时，瓦工需240小时;如果装修一套商品房，木工需180个工时，瓦工需300个小时。工程队现有18000个木工工时和15600个瓦工工时可供使用。若装修一套别墅利润为4万元，装修一套商品房利润为3万元，要制定这样的装修计划，能使这个工程队得到更多的利润？

设计意图：通过分析题意，归纳解决此类题型的主要步骤，目的是让学生加深对线性规划图解法的理解。让学生通过反复训练，不断加深对概念和方法的理解，培养学生的思维能力。

4.任务训练，巩固所学

任务1：某建筑材料厂生产甲乙两种新型建筑材料，已知生产甲种材料1t，需要消耗A种矿石10t，B种矿石5t，生产乙种材料1t，需要消耗A种矿石4t，B种矿石4t。每生产1t甲种建筑材料的利润是1500元，每生产1t乙种建筑材料的利润是1000元。该工厂在生产这两种产品的计划中要求消耗A种矿石不超过300t，B种矿石不超过200t。请问如何安排生产才能获取最大利润，并求出最大利润。

三、教学反思

1.合理改编教材，增加专业素材

本节课的教学内容，紧紧依托建筑专业背景，挖掘数学教学与建筑专业相关的教学素材，对数学教材进行灵活处理，将目前教师中普遍存在的“教教材”的观念转变到“用教材教”的观念，重新审视建筑专业的数学学习要求，在主体内容不变的前提下，有目的地整理教学内容，设计了一系列与建筑专业有关的数学问题与例题，对现有教材加工重组，突出与建筑专业相关联的内容，与之无关联的内容则可削减甚至删去，这是笔者对中职数学与建筑专业的有效整合。由此，笔者发现中职数学的教学必须将教材作为基础，创造性地优化教材资源，适当增加专业亮点，使所教内容更贴近建筑专业，激发学生的学习兴趣，让学生真正地理解、掌握数学知识和技能，提高数学素养。如本节课的教学中，典型例题中的问题1和问题2的设置，通过选取与建筑专业相关的实际问题，一方面让学生更好地理解线性规划的图解法，另一方面让学生体会数学的工具性和服务性功能。

2.突破传统教学，增添专业亮点

为实现数学教学与建筑专业课程的有效整合，教師需要改变传统教学方式，可以尝试使用案例教学法、任务导向法、实验法、小组合作学习等方式来开展日常教学工作。例如，在教学过程中，选择与建筑专业有关联的实验案例来开展教学，通过问题来引领学生，通过实验的方式获取相关数学知识，提高课堂教学的效果。通过改变传统教学模式，增加专业亮点，一方面能改变教师教授的方式，另一方面也能提高学生学习的积极性，培养学生的思维能力，使学生理解相应的数学知识、掌握相应的解题方法。另外，也能让学生去体会数学的工具性作用，以便更好地将数学知识服务于专业知识的学习。

当然，对于中职数学课程中最基础的知识，教师要在日常教学中讲细讲透，这些知识仍可以充分借鉴传统教学方式来进行。而对数学课程中的概念和定理，则可以利用信息化教学手段，并结合相关专业知识来形象化、生动化地展示出来，给学生以直观印象，便于学生理解掌握。

3.改变学习观念，体会服务意识

在本节课的教学设计中，通过与建筑专业相关的问题情境设置，改善传统数学课堂沉闷的气氛，让学生认识到数学知识与专业知识的紧密联系，让学生改变学习数学的传统观念，让学生不断提高数学学习的兴趣。另外，通过典型例题和练习的合理设置，让学生将数学理论知识与建筑专业实践项目整合在一起，充分发挥数学的工具作用，让学生体会到数学学习能更好地为专业服务。

总之，职业学校数学课程与专业课程的关系不容忽视，将两者进行有效的整合，要充分体现数学课程为专业课程服务的意识。在日常的数学教学中，教师应该架起数学学习与建筑专业课程学习的桥梁，强调数学与建筑专业的联系，从学生已有的专业素养出发，通过合理调整教学内容，恰当设置典型案例，让学生亲身体验将专业实际问题抽象成数学模型，利用数学知识和方法进行解答。只有当数学学习与学生的专业结合在一起，学生才能真正感受到学习数学是“有用”的，只有将“专业化”和“数学化”进行有机整合，才能实现职业学校数学课程“服务性、实用性”的理念，这也是笔者作为数学教育工作者追求的目标。

[参考文献]

[1]叶青林.中职数学在《建筑材料》课程教学中的应用.产业与科技论坛，2014（18）.

[2]黄兴华.基于建筑类专业的高职数学课程改革的几点思考.数理化研究，2015（11）.

[3]王茹.线性规划在实际生产生活中的应用.科技创新导报，2018（09）.