C-Cu共掺杂ZnO的p型导电性研究

丁罗城， 符斯列， 王春安, 李俊贤, 鲍佳怡, 秦盈星

(1.华南师范大学 物理与电信工程学院 广东省量子调控工程与材料重点实验室, 广州510006；2.华南师范大学华南先进光电子研究院，广州 510006；3.广东技术师范学院 电子与信息工程学院，广州 510665)

1 引 言

作为一种具有巨大潜能的新型半导体材料，ZnO是Ⅱ-Ⅵ族宽禁带直接带隙半导体，室温下禁带宽度约为3.37 eV，激子束缚能为60 meV，具有十分优良的光电特性[1-3]. 因此在发光二极管、光电探测器、表面声波器件及太阳能电池等领域有广泛的应用前景.获得性能稳定的p型ZnO是制备ZnO基光电器件的关键因素. 然而天然ZnO通常会产生氧空位和锌间隙原子，这些本征缺陷使ZnO呈n型导电性. 另外，ZnO的受主固溶度也低，因此人们希望通过掺杂改性获得稳定的p型ZnO[4, 5].

近年来，C、Cu单掺杂ZnO体系的磁电光性能研究比较广泛. 相对其他掺杂元素，C和Cu原料丰富、成本低廉、环境友好. 过渡金属Cu原子在ZnO中的固溶度也很高，有益于稳定掺杂. 在实验研究方面，Kim等采用磁控溅射法研究了Cu掺杂对ZnO体系的导电性能的影响，结果表明，在Cu掺杂摩尔量为0.01-0.03的范围内，Cu掺杂量越增加，掺杂体系电导率越强[6]；Pan等用激光脉冲沉积(PLD)方法研究了C掺杂ZnO体系，该体系导电性良好、铁磁性稳定且居里温度超过400 K[7]. 在理论计算研究方面，Nia等采用基于自旋极化密度泛函理论(DFT)的第一性原理研究了Cu掺杂ZnO磁特性的影响，结果表明，Cu单掺杂ZnO中，掺杂体系铁磁性稳定，Cu双掺杂ZnO中，掺杂体系稳定，p型导电性更优良[8, 9]；Yao等通过第一性原理计算了C单掺杂ZnO，其结果证明该体系可以获得稳定的p型ZnO结构[10]. 但对C-Cu共掺杂ZnO体系的第一性原理分析方面，尚未有研究. 因此，本研究采用基于自旋极化DFT的第一性原理研究了C-Cu以1:1、1:2和2:1比例条件下，共掺杂体系的晶格结构、态密度、有效质量和形成能等性质. 这对设计和制备新型理想的p型半导体材料有一定的理论指导作用.

2 理论模型与计算方法

2.1 理论模型

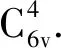
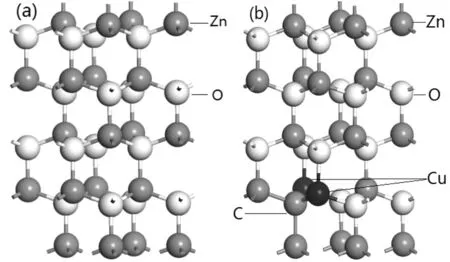
图1 超胞模型 (a) 本征ZnO超胞结构；(b) C-2Cu掺杂ZnO超胞结构Fig. 1 The supercell models (a) The structure of intrinsic ZnO supercell; (b) The structure of C-2Cu doped ZnO supercell

2.2 计算方法

本文采用CASTEP软件中的自旋DFT框架下的广义梯度近似(generalized gradient approximation,GGA)平面波赝势方法[12]，用Perdew-Burke-Ernzerhof泛函描述，对所有体系超晶胞模型进行了几何优化和能量计算[13, 14]. 利用数值化的原子轨道作基矢，基函数采用双指极基组[15]，迭代过程收敛精度为1×10-5eV,原子间相互作用力的收敛精度为0.03 eV/Å，晶体内应力收敛精度为0.05 GPa，原子的最大位移收敛精度为0.001 Å. 平面波截断能Ecut=380 eV，在优化系统结构和计算总能量时布里渊区的k空间网格点均为4×4×2，选取的ZnO，Cu，C的价电子组态分别为3d104s2, 2s22p4, 3d104s1, 2s22p2，其他轨道电子视为芯电子来计算.

3 结果与讨论

3.1 晶体结构分析

本文对所有掺杂体系进行了晶格优化，所得晶格参数如表1所示. 由表中数据可知，各掺杂体系晶体结构优化合理，且与文献[16]计算结果相近，误差远小于1%，确保了本文计算方法与结果的可靠性. 计算中C和Cu分别取代O和Zn,掺杂后体系体积都略有减小，由量子化学理论可知，这是由于C和Cu的离子半径均小于O和Zn的离子半径. 同时，Cu与Zn的原子半径相差不大，晶格尺寸失配小，可初步判定Cu掺杂ZnO形成能较低[17].

表1 ZnO各掺杂体系结构优化后的折合晶格常数

Table 1 The lattice parameters of each doped ZnO system after geometry optimized

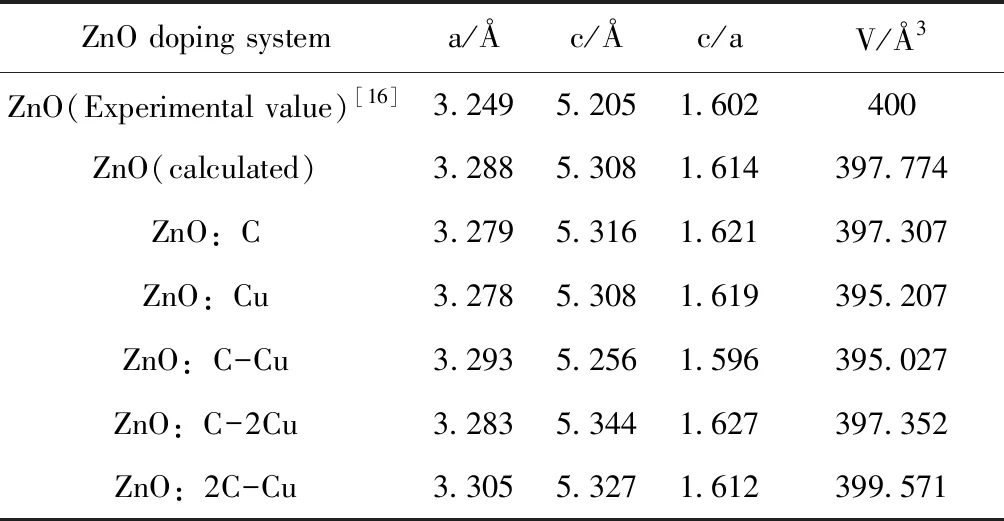
ZnO doping systema/Åc/Åc/aV/Å3ZnO(Experimental value)[16]3.2495.2051.602400ZnO(calculated)3.2885.3081.614397.774ZnO:C3.2795.3161.621397.307ZnO:Cu3.2785.3081.619395.207ZnO:C-Cu3.2935.2561.596395.027ZnO:C-2Cu3.2835.3441.627397.352ZnO:2C-Cu3.3055.3271.612399.571

3.2 能带结构和态密度分析

图2展示了未掺杂ZnO的电子结构，图中只给出了-6 eV-6 eV之间的能带结构以方便更细致的分析. 费米能级取能量零点. 从图中可以看出，价带顶和导带底均位于G点，表明为直接带隙半导体.禁带宽度Eg=0.73 eV. 此计算结果与文献[18]得到的完全一致，但比实验值(Eg=3.37 eV)偏低. 这并不影响对整体体系的电子结构定性分析. 这是由于在GGA模型中，Zn-3d态的能量被过高估计，使得其与O-2p态之间的相互作用增强，以致于价带带宽增大，且电子间的关联能作用被低估，从而计算得到的ZnO禁带宽度偏低，这种结果是采用该理论时的普遍现象[19]. 由图2可以看出本征ZnO的价带顶由p态决定，而价带是由s，p和d态杂化耦合形成；导带是由s和p态耦合形成，s态决定导带底的位置，d态对导带无影响.

图2 本征ZnO电子结构分布图Fig. 2 The distribution of electron structure of intrinsic ZnO

计算得出的C，Cu单掺杂ZnO的能带结构分布如图3(a)和(b)所示. 禁带宽度均有明显的变窄，导带向下扩展靠近费米能级. 费米能级附近产生杂质能级，且导带出现分裂. 由图3(a)、图3(b)与计算数据分析，费米能级已经进入价带，由此可初步分析掺杂后本征半导体均向p型半导体转变. C单掺杂ZnO体系中费米能级附近大部分被p态电子占据，由计算分析可知这种状态主要来自于C-2p态和O-2p态的杂化耦合. 而在Cu掺杂体系中，价带和导带下移，费米能级上存在半占据的空轨道，且费米能级附近的杂质能级主要来源于Cu-3d和O-2p之间的强烈杂化耦合.

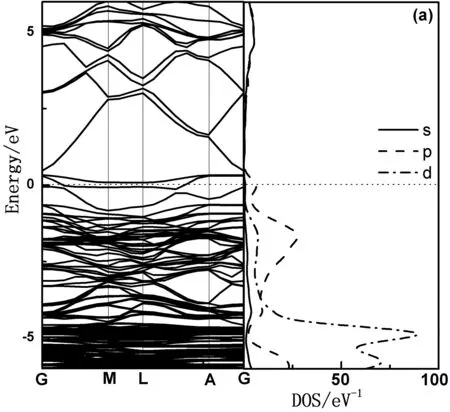
图3 电子结构分布图 (a) C单掺杂ZnO；(b) Cu单掺杂ZnOFig. 3 The distributions of electron structure (a) C-mono doped ZnO; (b) Cu-mono doped ZnO

当C、Cu共掺杂后，对比图3(a)-(b)以及图4(a)-(c)可知，共掺杂体系能级分裂明显，费米能级处能带结构更加弥散丰富，费米能级移入价带更深，p型化水平更高. 由图4(a)-(c)可看出，共掺杂体系价带主要分布在两部分. 下价带在-18 eV--10 eV附近，此部分主要由O的2s态和少量Zn的3d态贡献；另一部分分布在-6 eV-1 eV之间. -5 eV附近的能级主要来源于O的2p态、Zn的3d态、C的2p态以及Cu的3d态的强烈杂化耦合.随着激活原子Cu的掺杂及掺杂比例的提高，C-2Cu掺杂ZnO体系的总态密度值低于其他掺杂体系且峰值向低能量方向移动(如图4(b)所示). 表明该体系离域化更明显且有更好的电子迁移效应,这主要是因为掺杂了Cu以后C的2p态和Zn的3d态电子重叠加剧、轨道间吸引增强且Cu的3d态和C的2p态之间的强烈耦合效应使得C的p态电子向低能级移动. 然而，随着C元素掺杂比例的增加则会抵抗这种效应，电子迁移变弱.

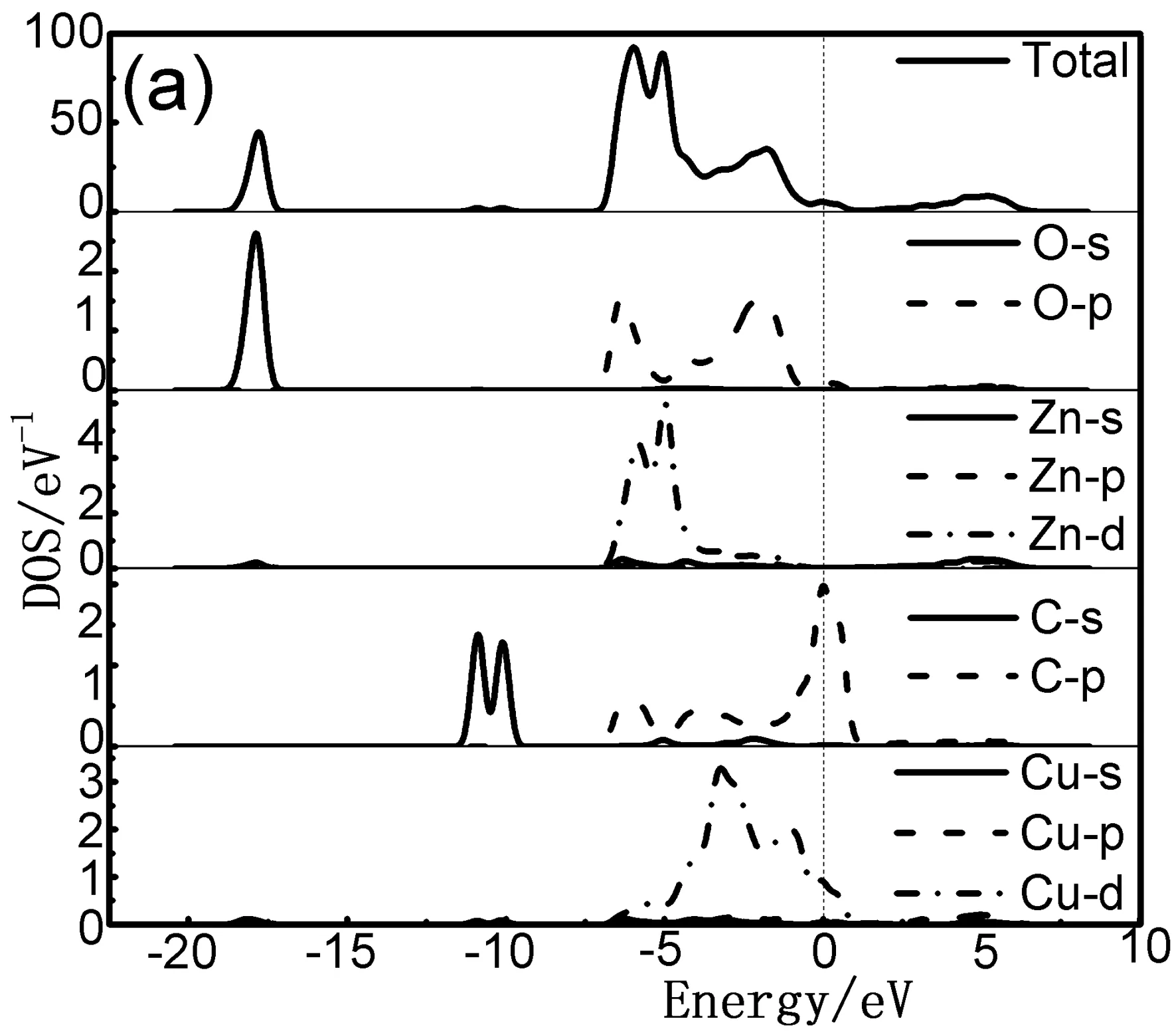
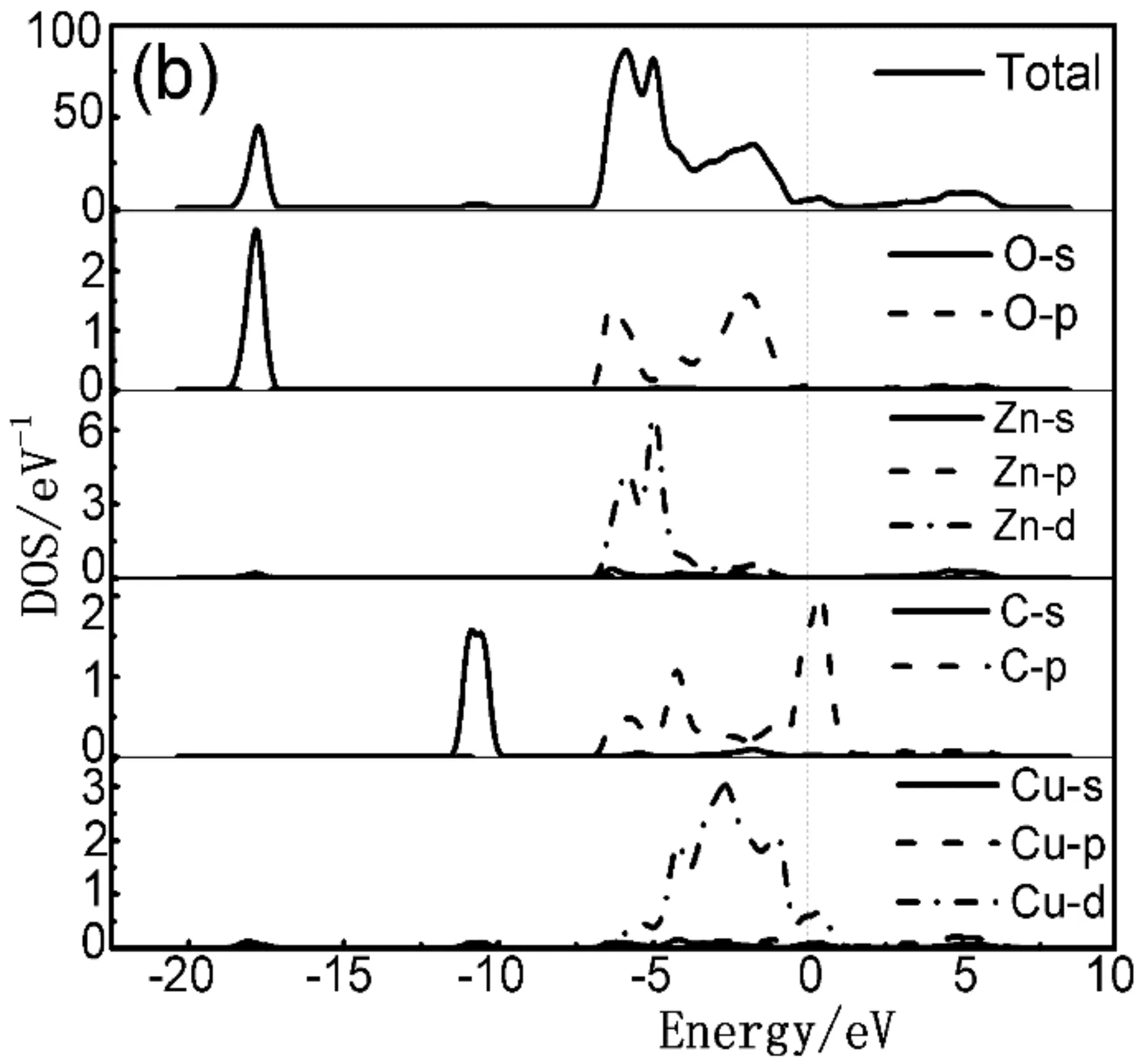
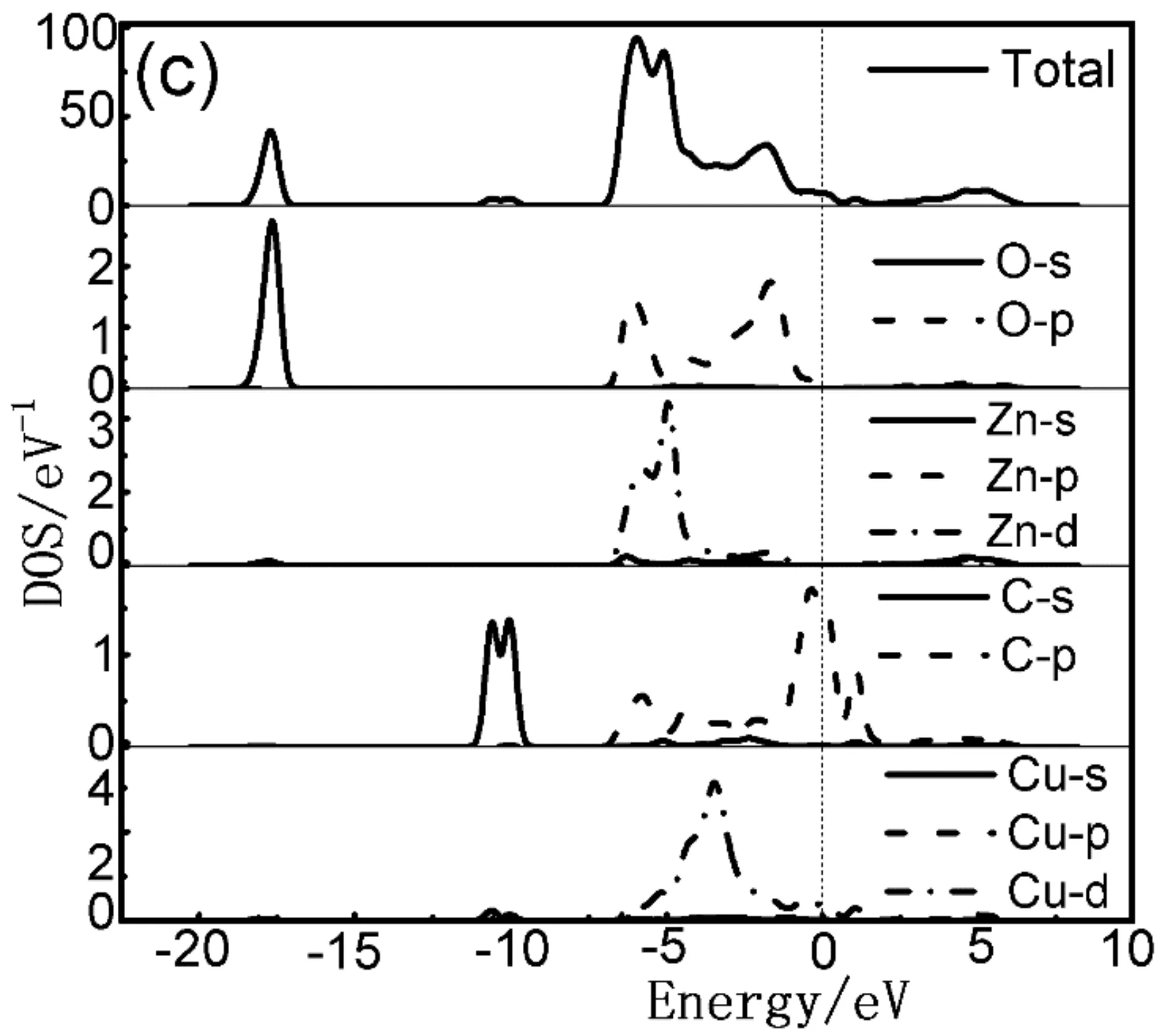
图4 共掺杂体系态密度图 (a) C-Cu掺杂ZnO；(b) C-2Cu掺杂ZnO；(c) 2C-Cu掺杂ZnOFig. 4 The densities of states (DOSs) of co-doped structure (a) C-Cu doped ZnO; (b) C-2Cu doped ZnO; (c) 2C-Cu doped ZnO

3.3 有效质量

为了更细致的研究ZnO各掺杂体系的导电性质，本文分别计算出了C单掺杂、Cu单掺杂以及C-Cu分别以1:1、1:2和2:1的比例共掺杂ZnO体系的空穴有效质量. 根据固体物理理论，空穴有效质量由以下公式[20]给出：

(1)

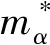
(2)

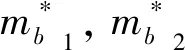
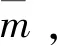
表2 各掺杂ZnO体系平均空穴有效质量

Table 2 The average effective hole masses of each doped ZnO system

有效质量C/m0Cu/m0C-Cu/m0C-2Cu/m02C-Cu/m0`m1.471.441.010.777.69

3.4 形成能分析

缺陷形成能Ef是反映和确定掺杂剂或缺陷溶解性能的重要物理因素. 掺杂体系形成能Ef的公式[22]为：

Ef=Eτ(defect)-Eτ(perfect)-∑iniμi,

(3)

式中，Eτ(defect)是掺杂体系的总能量，Eτ(perfect)是未掺杂晶体的总能量；ni代表超晶胞体系中掺入(ni>0)或移出(ni<0)的原子数量，μi为该原子所对应的化学势,取为掺杂元素基态的每个原子的能量. 由公式计算的形成能如表3所示. 表中计算结果表明：

表3 各掺杂ZnO体系的缺陷形成能

Table 3 The defect formation energies of each doped ZnO system

掺杂原子形成能/eVC2.308Cu-0.659C-Cu1.211C-2Cu0.5482C-Cu3.535

当Cu单掺杂时体系形成能最低，这与晶格结构的分析结果符合；C单掺杂形成能较高、固溶度低、不易掺杂,与Cu共掺后形成能明显降低更易于稳定掺杂；掺杂体系为2C-Cu时，形成能最大，而掺杂体系为C-2Cu时，形成能较小.

4 结 论

本文采用了基于密度泛函理论的第一性原理平面波超软赝势法，计算分析了C、Cu单掺杂，不同比例C-Cu共掺杂ZnO体系的几何结构、电子态密度、空穴有效质量和形成能. 结果表明：C、Cu单掺杂和不同比例C-Cu共掺杂ZnO体系均能获得p型导电性. 当C-Cu以1:2比例共掺时，杂质能级更加弥散，空穴有效质量最小，杂质形成能较低，容易获得p型化水平更高、电子迁移效应更好、掺杂更稳定的半导体新材料. 这为设计和制备更好的p型ZnO材料提供一定的理论借鉴价值.