二维激子极化激元凝聚中涡旋叠加态稳态及动力学特性研究

陈海军, 任 元, 王 华, 汤国志, 刘 通

(中国人民解放军战略支援部队航天工程大学, 北京 101416)

1 引 言

实验上实现了冷原子玻色爱因斯坦凝聚(BEC)以后, 与之相关的理论研究和实验研究层出不穷[1-4]. 实现冷原子BEC需要相当低的温度, 通常通过磁光阱和蒸发冷却技术来完成[5]. 低温下实现冷原子BEC, 给BEC的工程应用带来了限制. 近年来人们发现半导体微腔中的激子极化激元凝聚系统(exciton-polariton condensates)有望在室温下实现BEC[6], 给BEC的应用从实验室走向工程实践提供了可能. 激子极化激元BEC和冷原子BEC具有许多相同的性质, 例如在其中可以形成稳定的孤立子, 约瑟夫森振荡, 宏观自捕获和空间干涉等[7].

实现BEC以后, BEC超流特性的研究引起了足够重视, BEC中量子化涡旋的出现是BEC具有超流特性的直接证据[8]. 量子化涡旋的存在形式有单个涡旋, 涡旋阵列和正反涡旋叠加态.涡旋叠加态是由具有相同轨道角动量量子数的正反涡旋叠加形成涡旋叠加态. 2006年Liu M等人研究了单组分冷原子BEC中正反涡旋叠加态的基本性质, 并提出了一种产生正反涡旋叠加态的有效方案[9]. 2012年Thanvanthri S等人研究了基于原子BEC的正反涡旋叠加态在超稳物质波陀螺中的应用, 并首次提出了涡旋干涉陀螺的概念[10]. 2015年Padhi A N B等人研究了激子极化激元凝聚体系中单涡旋在旋转参考系中形成涡旋阵列中涡旋个数随系统参数的变化规律[11]. 2016年Dai W D等人进一步研究了扁平势和无序势中涡旋叠加态的稳态结构及其Sagnac效应, 理论阐明了涡旋干涉陀螺中Sagnac干涉相位, 轨道角动量量子数和半导体微腔旋转角速率三者之间的关系[12].

本文利用分步Crank-Nicolson方案的虚时和实时有限差分方法[13]求解耗散系统的Gross-Pitaevskii(GP)方程, 找出了谐振子势阱和高斯型势垒相结合的复合阱中的激子极化激元凝聚中正反涡旋叠加态的稳态结构, 并直观地验证这种稳态结构在半导体微腔旋转下的稳定性, 给出了稳定的涡旋叠加态和半导体微腔的旋转角速率之间的关系, 确定了涡旋叠加态在旋转参考系中具有Sagnac效应. 另外, 研究了泵浦光宽度和增益对系统中形成涡旋阵列动力学过程的影响.

本文的结构安排如下: 第二部分给出了描述耗散系统的无量纲化形式的GP方程, 系统的能量, 化学势, 角动量和自由能和数值计算方法. 第三部分讨论了正反涡旋叠加态的稳态结构. 第四部分给出了半导体微腔旋转下正反涡旋叠加态的稳定性及叠加态旋转角速率和半导体微腔旋转角速率之间的定量关系. 第五部分讨论了泵浦光宽度和增益对涡旋阵列形成动力学的影响.

2 理论模型和数值计算方法

2.1 GP方程和系统参数

(1)

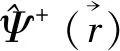
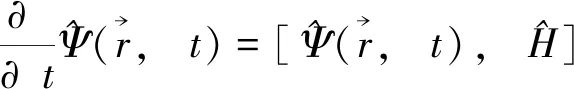
(2)

联合方程(1)和(2)得到

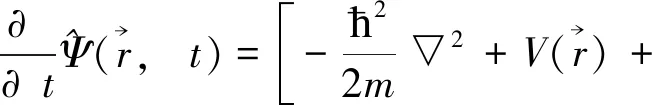
(3)

在零温极限下, 采取Bogoliubov近似, 把场算符用波函数替代, 得到描述玻色体系动力学行为的Gross-Pitaevskii方程.

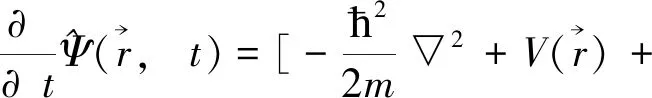
(4)

其中g=4πħ2a/m表示粒子之间的两体相互作用强度.

对于弱相互作用的激子极化激元体系仍然可以用方程(4)描述其动力学过程. 由于激子极化激元系统中存在泵浦和损耗, 是非平衡系统, 因此要在方程(4)的基础上加入耗散项和增益项.另外, 为了研究半导体微腔旋转时体系的动力学特性, 还要引入旋转项. 方程(4)是三维方程, 我们考虑的是准二维体系, 因此要在冻结z方向自由度的基础上对方程进行约化处理得到二维方程. 另外, 为了数值计算方便, 我们选取体系的特征长度, 时间和能量

t0=1/ω～ps

E0=ħω～0.66 meV

(5)

对方程进行无量纲化处理. 最终得到的无量纲化GP方程为

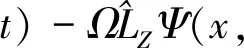
(6)

为了研究系统的稳态结构和涡旋演化动力学过程, 数值计算过程中可以根据系统参数的变化趋势来判断系统是否达到稳态, 包括系统能量, 耗散能和化学势.在单涡旋向涡旋阵列的演化过程中, 自由能的变化尤为重要, 它们的表达式分别是

▽Ψ|2+

(7)

2.2 数值计算方法

由于激子极化激元凝聚系统存在粒子数的增加和损耗, 而虚时演化方法每一步数值计算对波函数进行了归一化, 相当于忽略了粒子数的损耗和增加, 因此不能直接利用虚时演化方法求解激子极化激元系统的稳态解. 我们采用的方法是先忽略方程(6)中的虚数项, 利用虚时演化方法找出不存在泵浦, 损耗和增益的情况下, 系统的稳态解, 然后利用实时演化方法, 验证加上泵浦, 损耗和增益时, 稳态解能够稳定存在所对应的泵浦, 损耗和增益值, 这样就找出了特定参数下激子极化激元系统中稳定的涡旋叠加态.

谐振子系统的基态解形式是高斯型, 因此数值计算过程中, 我们选用如下形式的高斯型涡旋叠加态函数作为初始波函数.

[(x+iy)l1+(x-iy)l2]

(8)

w是初始波包的宽度,l1和l2是涡旋量子数, 根据其不同取值可以构造出单涡旋态和正反涡旋叠加态, 尤其当l1=l2=l时, 所形成的正反涡旋叠加态呈现对称的“花瓣”状, 花瓣的个数为2l.

3 涡旋叠加态的稳态结构

图1是虚时演化结果. 只存在谐振子势阱时, 系统的稳态解应为高斯型函数, 当给定正反涡旋叠加态时, 最终也会演化为高斯型. 为了阻止这种演化, 形成稳定的正反涡旋叠加态, 在谐振势阱中央加入一个高斯型势垒阻止这种演化, 表达式为

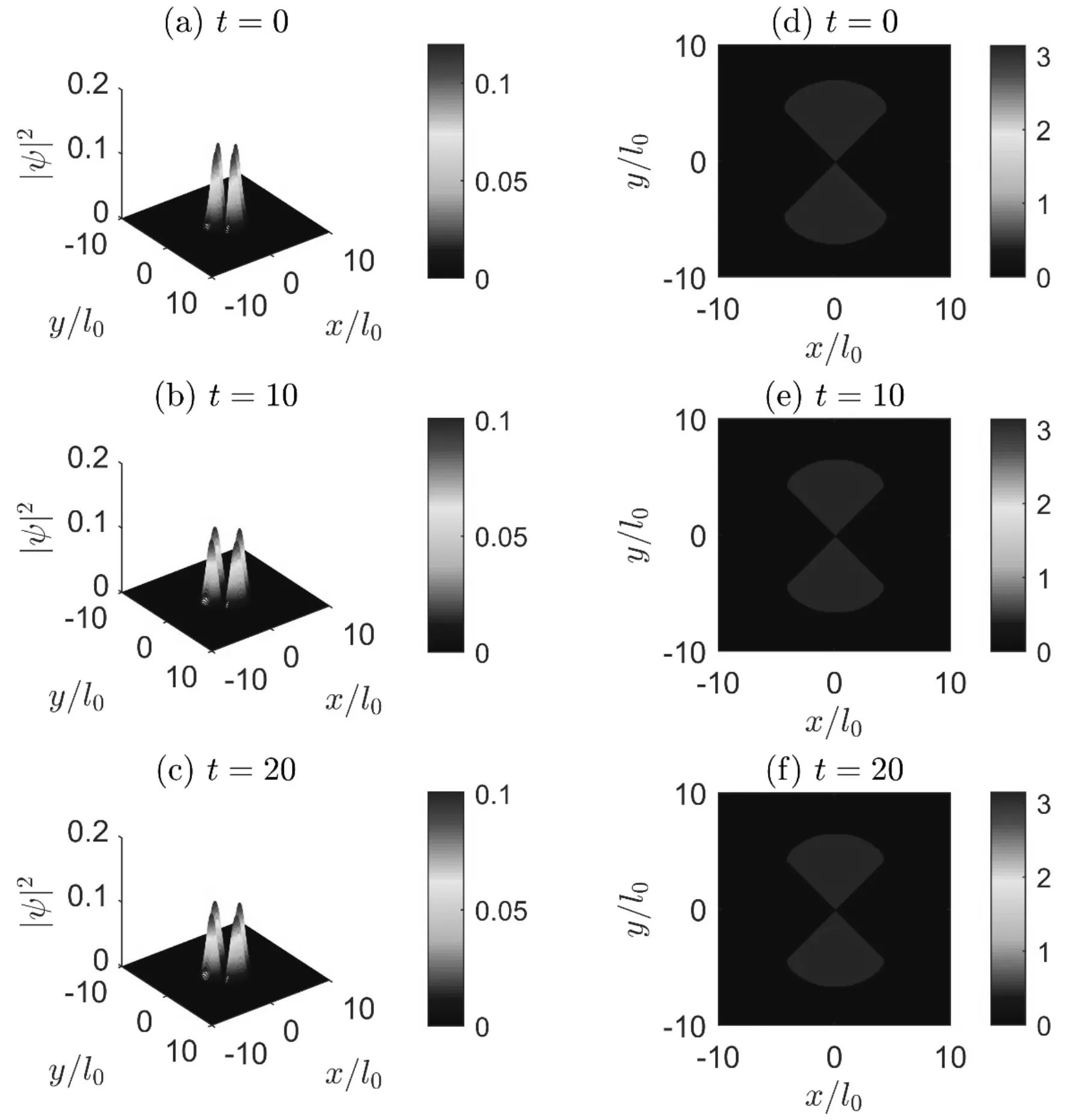
图1 虚时演化方法计算稳态结构的过程, l=2, g=1, wc=1.2, wb=1.2, b0=10.5Fig. 1 The process of calculating steady-state structure imaginary-time propagation method, l=2, g=1, wc=1.2, wb=1.2, b0=10.5

b0exp[-(x2+y2)/(2wb)]

b0和wb分别表示势垒的高度和宽度, 这样所形成的简谐势阱和势垒叠加的囚禁结构类似于文献[22]中提出的墨西哥帽子势阱.t=0时,m=2, 花瓣的个数为4, (a)给出初始时刻体系的密度分布|Ψ(x,y)|2(红的部分密度大, 蓝的部分密度小, 下同), 涡旋量子数是2, 呈现花瓣数为4的对称状态. 为了数值计算的稳定性, 非线性相互作用项g随时间逐渐增加. (b)给出非线性相互作用项达到预定值时系统的密度分布. (c)表示经过一定时间演化所形成的稳态结构, 判断系统达到稳态的标准是系统参数(能量, 化学势, 自由能)不随时间进行变化, 保证在一定的误差范围内波动. (d)(e)(f)是和上述密度分布所对应的相位分布. 可以看出, 给定初态后, 经过很短时间的

演化系统就行形成了稳态结构, 稳态结构和初态结构不同, 这是由于谐振子势阱和中心势垒所形成的环状囚禁区域, 使得粒子沿着圆环方向分布, 形成稳定的花瓣结构.

图1是无虚数项时用虚时演化方法的到的稳态结果, 保持所有参数取值不变, 当加上虚数项时(泵浦、损耗和增益), 这时虚时演化结果一般不再是系统的稳态结构.为了使无虚数项时的稳态结构在加上虚数项时仍然是体系的稳态结构, 必须使虚数部分ρ-γ-η|Ψ|2总体效应为0, 由此结论可以得出|Ψ|2=(ρ-γ)/η, 同时|Ψ|2还受制于方程(6)中其它部分的制约.我们的计算方案是给定损耗和饱和增益项, 然后根据系统参数(7)随时间演化趋势调整泵浦功率, 当泵浦功率取某一合适值时, 泵浦, 损耗和增益项互相平衡, 系统参数维持稳定状态不随时间变化, 此时的泵浦功率为临界泵浦功率.

在计算过程中, 粒子之间的两体相互作用强度g=1, 损耗和增益饱和项取η=γ=0.001, 泵浦光宽度wp=6. 图2第一行和第二行分别给出稳定正反涡旋叠加态结构的密度和相位分布.前三列表示无虚数项的情况; 后三列表示存在泵浦, 损耗和增益的情况, 对应的临界泵浦功率分别是,

p1=0.00115442,p2=0.00222305,

p3=0.00273581,

(9)

第一, 四列涡旋量子数l=2, 势垒宽度和高度分别是wb=1.2,b0=10.5; 第二, 四列m=3,wb=2.6,b0=400；第三, 六列m=4,wb=2.6,b0=1200.

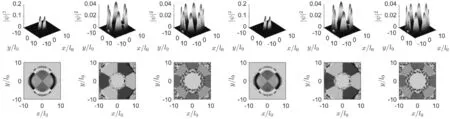
图2 l=2, 3, 4三种情况下有无GP方程中虚数项对应的稳态结构密度和相位分布Fig. 2 Steady-State structure density and phase distribution in GP equation without imaginary and imaginary items for l=2, 3, 4

可以看出随着涡旋量子数增加, 离心势能逐渐增加, 正反涡旋叠加态半径和能量随之增加;相同涡旋量子数条件下, 有无虚数项所得到稳态结果完全一致, 说明泵浦, 损耗和增益饱和三项只要达到平衡, 不会对稳定状态的结构有所影响;涡旋量子数越大, 需要的泵浦光强度越大, 势垒强度和宽度也随之增加.

4 旋转情况

4.1 涡旋叠加态的Sagnac效应验证

为了研究激子极化激元凝聚体系中的超流特性, 涡旋动力学是其中重要的研究内容. 我们考虑了正反涡旋叠加态(l=2)的旋转动力学特征. 由于正反涡旋叠加态的总角动量为0, 当体系旋转时, 正反涡旋会产生附加的相位差, 导致密度分布所形成的花瓣整体旋转.

图3给出了l=2的正反涡旋叠加态在半导体微腔角速率Ω=0.1ω时随时间演化的动力学过程, 第一, 二行分别表示不同时刻的密度分布和相位分布(a)-(f). 可以看出, 一方面, 当凝聚体随着体系一起旋转时, 初始给定的正反涡旋叠加态的密度和相位分布整体形状不随时间变化, 说明涡旋叠加态是长时间稳定的(计算时长为500); 另一方面, (g)图表示密度分布沿x轴的截面图随时间变化情况, 可以看出截面图随时间分布周期性地交替变化, 说明叠加态的转动是匀速的, 为了讨论旋转速度的具体大小, 我们考虑了1/4周期内的旋转情况, 从(h)图可以看出, 叠加态1/4周期大约是16 ps, 则时间周期是64, 根据T=2π/Ω=2π/0.1≈63, 和我们数值计算结果一致.

图3 l=2的稳定涡旋叠加态随时间的旋转过程Fig. 3 The rotational process of a stable vortex superposition state over time for l=2

4.2 涡旋叠加态的旋转角速率

为了进一步阐明涡旋叠加态的旋转角速率, 半导体微腔角速率和涡旋轨道角动量量子数三者之间的关系, 我们进一步在不同轨道角动量量子数与半导体微腔旋转速率的条件下进行对比计算, 结果如图4所示. 从图4(a)可知, 叠加态的转动周期Ti随着半导体微腔速度Ω的增加而减小, 且与涡旋轨道角动量l没有关系. 图4(b)进一步给出了叠加态旋转速率Ωi和Ω之间的关系, 可以看出, 在不同l取值下, Ωi和Ω始终相等. 以上分析表明, 叠加态BEC和惯性空间之间是相对稳定的.

事实上, 根据图3(g), 我们可以定义干涉图样变化频率为fd=1/△Td, 其中△Td表示在微腔角速率为Ω的条件下实现某一时刻涡旋密度分布与静态条件下的涡旋密度分布完全一致所用的最短时间. 图5给出了不同轨道角动量量子数下花瓣重合速度(涡旋密度变化速率)Ωd与微腔角速率Ω之间的关系. 从图5可以看出, 在给定l的条件下, 涡旋密度变化速率Ωd与微腔角速率Ω成正比例关系, 且其斜率满足关系Ωd/Ω=2l, 即在轨道角动量量子数为2,3,4的情况下, 斜率分别为4,6,8. 因此密度分布的相位变化是

Δφd=ΩdTd=2/ΩTd

(10)

图4 叠加态旋转周期和速率与微腔旋转角速率之间关系Fig. 4 Relationship between rotation period and rate of superposition state and the rotational angular rate of microcavity

文献[11]稳定情况下的密度分布为

[1+cos(2|l|φ)]|Ψ(|l|,ρ,z)|2

(11)

旋转相位Δφd后, 密度分布应为

[1+cos(2|l|φ+ΩdΔT))]|Ψ(|l|,ρ,z)|2

(12)

与文献[11]中的结论一致.

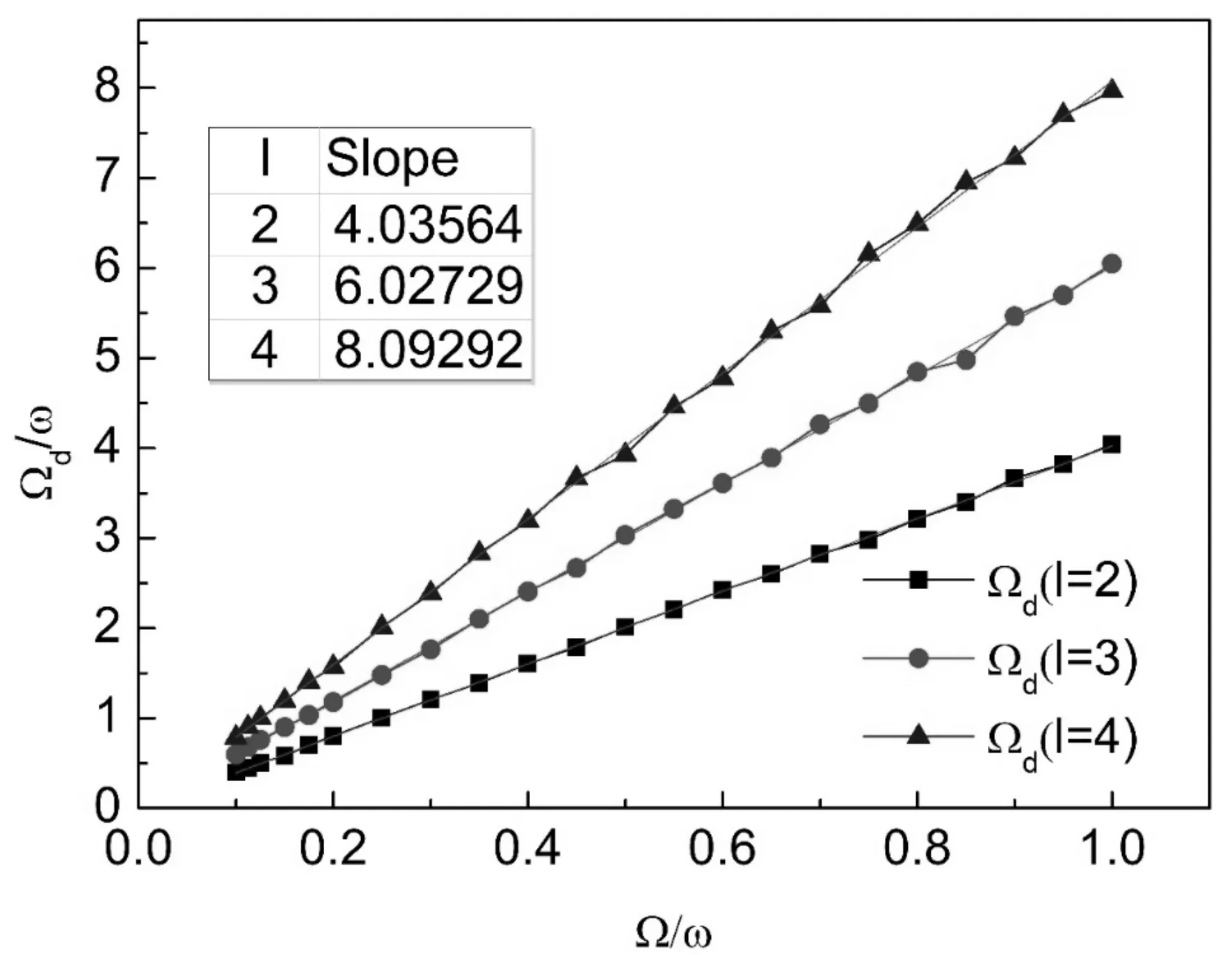
图5 密度变化频率随微腔角速率变化Fig. 5 Variation of density change frequency with the angular velocity of microcavity

5 单涡旋态的动力学演化过程

图6 旋转参考系中涡旋晶格随泵浦光宽度的变化, l=1, g=10, p=2, η=γ=1, wc=1.2Fig. 6 The change of vortex array in rotating reference system with the width of pumped light, l=1, g=10, p=2, η=γ=1, wc=1.2

单涡旋态的动力学演化过程如图6和7所示, 给出了复数项中高斯型泵浦光宽度wp和增益饱和项η对动力学演化过程的影响. 我们取Ω=0.95ω研究旋转带来的动力学过程, 根据超流的特性, 当体系的旋转速率超过某一临界值时, 体系中会出现三角形排列的涡旋晶格, 我们的计算结果也是如此.

图7 旋转参考系中涡旋晶格随增益饱和项的变化, l=1, g=1, p=2, γ=1, wp=5.5, wc=1.2Fig. 7 The change of vortex array with gain saturation in rotating reference system, l=1, g=1, p=2, γ=1, wp=5.5, wc=1.2

图6给出的是激光宽度对动力学过程的影响, 从上到下每一行对应的泵浦光宽度分别是wp=4.5, 5.0, 5.5, 6.0, 6.5, 7.0, 第一列对应t=500时的粒子密度分布, 第二列是和第一列对应的相位分布. 主要结果有: (1) 由于激子极化激元凝聚是激子和光子的耦合叠加态, 涡旋区域随着泵浦光宽度的增加而增加. (2) 涡旋是从凝聚体边缘逐渐进入中心, 进入时间随着激光宽度增加而提前,wp=4.5时在我们计算的时间范围内没有涡旋进入凝聚体,wp=7.0时在很短时间内就有涡旋进入凝聚体. (3) 涡旋阵列呈三角形排列, 涡旋个数随泵浦光宽度增加而增加. (4) 初始状态的中心涡旋随着时间演化会突然消失, 进而以小涡旋形式代替.

图7是动力学过程随饱和增益项η的变化, 从上到下每行对应的饱和增益项分别是η=0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 每一列的的含义和图6一致, 可以看出: (1) 涡旋从边缘进入凝聚体的时间随η的增加而提前, 并且涡旋个数随η增加而减少. (2) 涡旋区域大小没有明显变化. (3) 中心涡旋随着时间增加会分裂成小涡旋, 并偏离中央区域, 分裂时间没有明显规律, 图6当wp=4.5时, 在计算时间内没有涡旋进入凝聚体系, 中央涡旋也没有产生分裂, 图7中当η=1.3时, 虽然有涡旋较早进入凝聚体系, 但是在计算的时间内, 中央涡旋没有产生分裂. 从动力学过程中可以看出, 虽然能量, 化学势等物理参数不随时间变化, 但是最终的涡旋晶格状态是动态变化的.

6 结 论

通过虚时和实时演化方法求解耗散GP方程研究了谐振子势阱和高斯型势垒叠加形成的类墨西哥帽子势阱中正反涡旋叠加态的稳态结构, 旋转动力学过程以及泵浦光宽度和增益对单涡旋演化成涡旋阵列过程的影响. 由于耗散GP方程中包含泵浦, 损耗和增益饱和项, 不能直接利用虚时演化方法求解系统的稳态解, 可以利用虚实演化相结合的方法研究稳态结构和实时方法经过长时间演化研究系统的稳态结构和动力学过程.

在此复合势阱中可以形成不同轨道角动量量子数的稳定叠加态, 且其可以在旋转条件下保持稳定. 涡旋叠加态形成的干涉图样相对于惯性空间是稳定的, 且涡旋密度分布的变化速率正比于半导体微腔的旋转速率和角动量量子数, 这与基于Sagnac效应的理论分析结果一致. 单涡旋态在高速旋转情况下会形成涡旋晶格, 涡旋晶格是超流体的特征之一, 证明了激子极化激元凝聚具有超流性, 并且证明泵浦光宽度和增益饱和项对涡旋阵列结构有明显影响.