大尺寸核/层Co-Pd合金团簇稳定结构研究

吴 夏， 李小凡， 张少勇， 刘 涛， 徐义庆

(安庆师范大学化学化工学院 光电磁功能材料安徽省重点实验室 光电磁功能配合物和纳米配合物安徽省重点实验室，安庆 246011)

1 引 言

在材料化学与计算化学领域，金属纳米团簇的稳定结构及性质研究成为热点问题[1, 2]．与金属原子及其块体材料相比，金属纳米团簇具有更为特殊的物理和化学特性．从科技和经济视角来看，当制备由昂贵元素构成的表面活泼纳米粒子，且合金团簇的内核原子与环境无直接作用或者相互作用仅限于表面作用时，应避免使用纯的昂贵金属或稀有元素，可减小消耗．比如，Pd是一种昂贵的元素，其纳米团簇或纳米粒子被广泛用于反应的催化剂．核层结构中Pd位于外层的核层结构吸引了广泛的兴趣[3]．

相比于单一元素金属团簇，对二元团簇结构确定的计算难度要大很多，且关于Co-Pd二元团簇方面的理论计算也较少.例如，采用Sutton-Chen势函数，使用蒙特卡洛(Monte Carlo)算法及Basin hopping算法优化Co-Pd(N= 11-20)二元金属团簇稳定结构及能量[4]，大部分结构采取二十面体结构．此外，该函数还被用于研究13及19原子Pd-Co团簇的热熔性质[5]．基于Gupta势函数的遗传算法(GA)也被用于研究Co-Pd团簇结构[6,7]，密度泛函理论(DFT)[8]和广义梯度近似(GGA)算法计算Co-Pd的混合结构和核壳团簇结构性质[6,8]．Aguilera-Granja等研究了26原子的CoPd团簇的构型、电子结构、磁性和金属行为[9]．基于MgO(001)载体的34与38原子CoPd纳米团簇的结构及化学序列[10].

确定团簇稳定结构尤其是二元或更多元团簇稳定结构是一项艰巨的任务．早期开发的全局优化算法主要是为了解决单一原子类型团簇的结构优化，其中具有代表性的算法包括GA[11]、Basin-hopping(BH)算法[12]、快速退火算法(FAEA)[13]、自适应免疫优化算法(AIOA)[14]、动态格点搜索算法(DLS)[15]等．而在二元或多元团簇中，即使团簇拥有相同的结构类型，也存在着由于不同类型原子相对位置上的差异产生的homotop同分异构问题．因此，用于二元团簇结构优化的算法需同时解决构型异构及homotop异构难题．为此，常使用原子交换操作来解决homotop问题，并改进了GA、BH及AIOA算法用于二元团簇的结构优化[16-20].

本文采用基于内核构建的AIOA算法(称之为AIOA-IC算法)[20]优化原子总数为98和147的Co-Pd团簇最稳定结构，并使用多体Gupta势函数描述Co-Pd团簇原子间相互作用．结果显示98原子Co-Pd团簇包含了多种结构类型，并呈现出Co核/Pd层的结构特点．此外，还分析了键数、平均键长、序列参数、过剩能量值等性质．

2 计算方法

采取Gupta多体势函数来描述Co-Pd合金团簇中Co-Co、Co-Pd和Pd-Pd原子间相互作用．基于紧束缚二阶近似的Gupta势函数常被用于分析金属团簇稳定结构和溶化行为等性质[21-23]．对于原子总数为N的Co-Pd团簇，多体Gupta势函数形式描述为：

(1)

(2)

(3)

其中，Vr(i)和Vm(i)分别为斥力项和引力项，rij是原子i和j之间的距离．描述Co-Pd团簇原子间相互作用的Aij、ξij、pij及qij参数摘自Cleri和Rosato对块体材料结合能、晶格参数和独立弹性常数等实验值的拟合[21]，列于表1中.

表1 Co-Pd团簇Gupta势函数参数

Table 1 Potential parameters of Co-Pd clusters with the Gupta potential

组成Aij(eV)ξij(eV)pijqijr(0)ij(Å)Co-Co0.17571.8439.212.9752.500Pd-Pd0.17461.718010.8673.7422.7485Co-Pd0.175151.780510.03853.35852.62425

应用AIOA-IC算法优化大尺寸Co-Pd合金团簇的最稳定结构．其具体流程描述如下：1)随机产生Nlib个初始结构并组成初始基因库．研究显示合金团簇可能存在十面体、二十面体、面心立方(fcc)、六折叠、Leary四面体(LT)结构等结构类型，这里选用这些结构作为初始结构的内核，而多余的原子则随机地分散在内核的外围．然后，调用限制内存的类牛顿算法(LBFGS)对这些结构进行局部优化操作[24]，这些初始结构构成了初代(it= 0)基因库．2)执行免疫克隆操作，通过运用免疫选择程序从第it代基因库中选出Npop个体．个体被选择的概率由基因库中个体的适应值(势函数能量值)来确定．3)执行变异操作．该操作分为两个方面：针对团簇的几何异构体问题，采用50%的概率用于将个体中能量高的原子随机地移动到团簇的表面，以快速降低团簇的能量；对于homotop同分异构问题，使用剩余50%概率采用随机地选择一对异种类型的原子再交换其原子类型(原子交换)的方式．4)采取更新操作，将能量更低的新结构保留于基因库中．5)此时，it=it+ 1．当达到既定的循环次数Nloop时，即终止运行本次AIOA-IC算法．能量最低的团簇结构即为全局最优结构，否则，程序转到步骤2．本研究中，运行参数设置为Nlib= 20、Npop= 20及Nloop= 1500，程序运行次数为100次．

3 结果与讨论

3.1 ConPd98-n团簇最优结构

为研究原子总数为98及147的Co-Pd合金团簇稳定结构，使用AIOA方法对纯Co和Pd金属团簇作结构优化，Co98、Co147、Pd98及Pd147团簇的最优结构绘制于图1中．如图1所示，Co98是具有堆积缺陷的双面心立方结构，Pd98拥有十面体结构类型．Co147为完整的Mackay二十面体结构，Pd147是拥有反层的十面体结构．

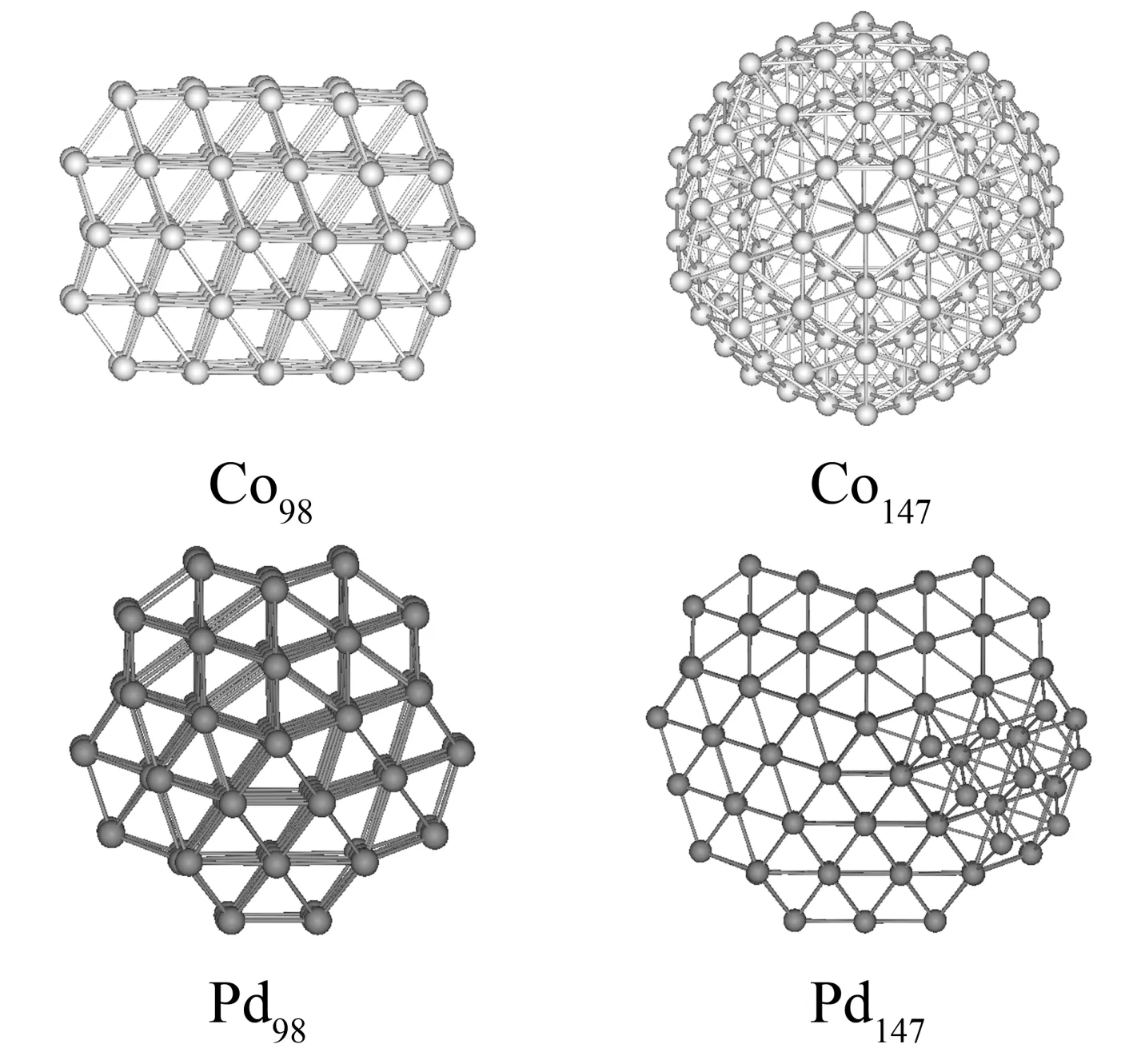
图1 双面心立方Co98、二十面体Co147、十面体Pd98与拥有反层十面体Pd147团簇的稳定结构Fig. 1 Geometrical structures of twin face centered cubic (fcc) Co98, complete Mackay icosahedral Co147, decahedral Pd98 and decahedron with anti-layer Pd147 clusters

图2和3绘制了由AIOA-IC算法优化得到的ConPd98-n(n= 1-98)团簇最稳定结构．如图所示，团簇结构可分为面心立方结构、Mackay二十面体、双二十面体、由双二十面体面面相连构成的结构和十面体结构．首先，Co1Pd97、Co2Pd96和Co3Pd95为面心立方结构．特别地，从Pd98到Co1Pd97，结构出现了原子重排现象，由十面体转变为面心立方结构．这种现象常出现于小尺寸合金团簇中，而在98原子Co-Pd团簇中也出现了这种现象．随着Co原子数目从4增加到24，除了Co16Pd82、Co17Pd81、Co22Pd76和Co24Pd74为由双二十面体面面相连构成的结构之外，其余均为基于Mackay二十面体的结构．ConPd98-n(n= 25-30)团簇为双二十面体结构．ConPd98-n(n= 31-54)团簇中，除了在n= 35、38、46、48、50、51与53处为双二十面体结构之外，其余均为基于Mackay二十面体的结构．随着Co原子数由55变化到85，团簇均为基于Mackay二十面体的结构．随后，当ConPd98-n(n= 86-97)时，团簇为十面体结构．而从Co97Pd1变化到Co98时，一个Pd原子被Co替换后，结构由十面体变为有堆积缺陷的面心立方结构，出现了原子重排现象．由此可见，98原子Co-Pd合金团簇中，绝大部分团簇采取二十面体的结构类型，部分采用十面体和面心立方结构类型．而最优结构中并未出现Leary四面体结构类型.

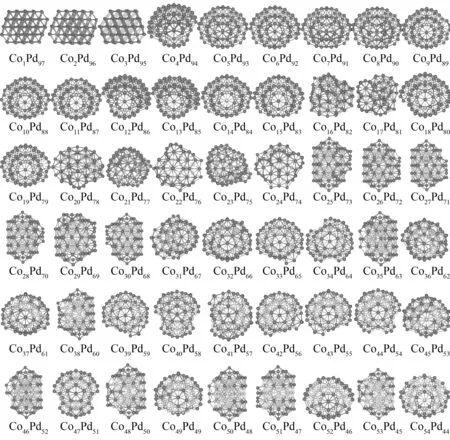
图2 随着Co原子数从1变化到54，ConPd98-n团簇结构变化规律，Co和Pd原子分别用浅色和深色表示Fig. 2 Variation of structres of ConPd98-n (n = 1-54) clusters, and Co and Pd atoms are represented by light and dark spheres, repectively.

3.2 键数分析

图4显示了ConPd98-n(n= 1-97)团簇中Co-Co、Co-Pd、Pd-Pd键数以及总键数．如图4所示，当n≤ 24时，总键数数目为427．在该尺寸范围内，主要为面心立方结构和基于Mackay二十面体的结构，如上所述．当n= 25-87时，大部分团簇组成的总键数为432．这此区间内，除了在n= 86和87时为十面体结构外，其余结构为双二十面体结构和Mackay二十面体结构．而随着n值从88增长到97，十面体Co-Pd团簇的总键数呈现出先增长后降低的趋势．此外，随着n值的增加，即Co原子数目的增加，Co-Co键数呈现不断上升趋势，Pd-Pd键数表现出不断减少的趋势，而Co-Pd键数由上升变化为下降．

图4 ConPd98-n (n = 1 - 97)团簇结构中Co-Co、Co-Pd、Pd-Pd键键数及总键数Fig. 4 Bond numbers of Co-Co, Co-Pd, and Pd-Pd and total number in ConPd98-n (n = 1-97) clusters.

3.3 序列参数及稳定性

序列参数(R)被用来表示Co-Pd团簇结构中Co和Pd原子的分布规律．Co和Pd原子到团簇结构中心的距离定义为R值，其形式表示为：

(4)

其中，xi、yi、zi为原子坐标值．可以根据R值的大小来判断Co和Pd原子到结构中心的距离．Co或Pd原子的R值偏大或偏小说明其倾向于分布在结构的表面或内层，而位于中间大小的R值则可以得出团簇趋于形成原子混合模式的结论．

图5显示了ConPd98-n(n= 1-98)团簇中Co和Pd的序列参数值．如图所示，对所有的团簇组成，RCo值大于RPd值．说明Co-Pd团簇中Co和Pd原子处于分离状态，即Pd原子趋于分布在团簇的表面，而Co原子位于结构的内层．图6绘制了ConPd98-n(n= 1-97)团簇过剩能量值变化．图中所有组分的过剩能量值为负值，说明Co和Pd具有一定的混合性，且在组成为Co35Pd63时原子混合得最为充分．

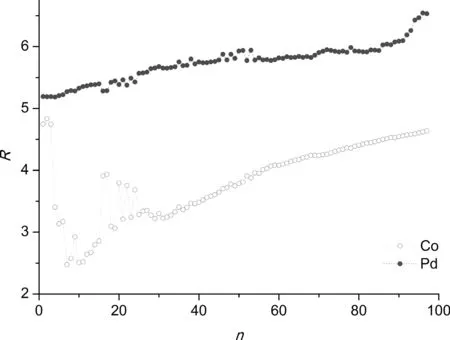
图5 ConPd98-n(n = 1-98)团簇的序列参数变化规律Fig. 5 Variations of the order parameters of ConPd98-n (n = 1-97) clusters

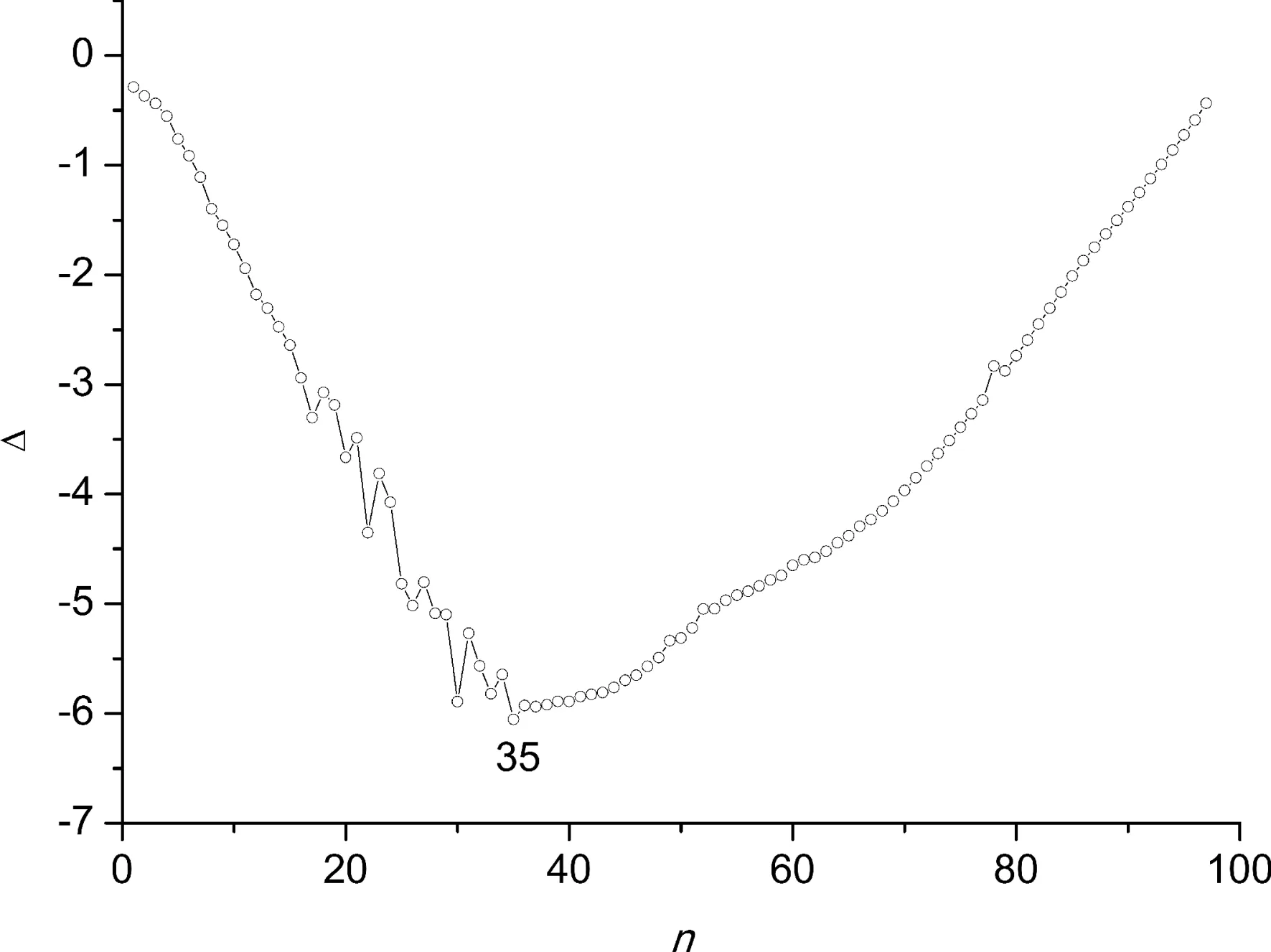
图6 ConPd98-n (n = 1-97) 团簇过剩能量值变化Fig. 6 Excess energies of ConPd98-n (n = 1-97) clusters

3.4 147原子二十面体结构

使用该方法优化了原子数目为147的Co-Pd团簇最稳定结构，结果显示这些团簇均为完整二十面体结构．图7中绘制了六个具有代表性的团簇结构．首先，Co13Pd134团簇的最内层(内核)被13个Co原子占据，Pd原子位于外层．Co55Pd92团簇的内核和次外层全部被55个Co原子占据．随着Co原子数目的增加，如Co92Pd55、Co98Pd49、Co127Pd20和Co135Pd12团簇所示，Co原子逐渐占据二十面体的次外层和最外层格点．Co135Pd12团簇最外层的12个顶点全部被Pd原子所占据．原子半径和表面能可用于解释Co和Pd原子的分布规律[25,26]．Co和Pd的原子半径分别为1.25 Å和1.37 Å，表面能分别为159 meV Å-2和125-131 meV Å-2．可见，Pd原子半径大，且表面能更小，易于生长于团簇的外层．

图7 典型的二十面体ConPd147-n团簇结构的直视图及截面图Fig. 7 Complete Mackay icosahedral structures and their sectional views of typical 147-atom Co-Pd clusters.

4 结 论

使用基于内核构建的自适应免疫优化算法确定由多体Gupta势函数描述原子间相互作用的Co-Pd团簇最稳定结构．对于98原子Co-Pd团簇，结构可分为面心立方结构、Mackay二十面体、双二十面体、由双二十面体面面相连构成的结构和十面体结构．序列参数显示Co原子位于内层，而Pd原子位于外层．原子半径和表面能进一步解释了Co和Pd原子的分布规律．原子数目为147的Co-Pd团簇均为完整二十面体结构．