CN+离子电子结构和跃迁性质的理论研究
2019-04-29徐建刚况昊南张云光
徐建刚, 况昊南, 窦 戈, 崔 洁, 张云光
(西安邮电大学理学院, 西安 710121)
1 引 言
分子离子是自然界中普遍存在的物质形态, 阳离子的电子结构和光谱性质是研究彗星尾部、恒星大气和星际空间中所发生的物理及化学变化的基础. CN+与CN-离子是天体物理和大气科学研究中的重要部分[1]. 在上个世纪中期, Douglas和Routly(1954)[2]首先在实验上对CN+离子的光谱进行了研究, 报道了两种1Σ-1Σ类型的波段. 自此开始, CN+离子的研究开始映入人们的眼帘, 越来越多的实验[3]和理论[4-17]研究被报道.
1970年, Lutz[3]报道了CN+离子的辐射光谱(1Π-1Π), 同时对a1Σ+、b1Π、c1Σ+、d1Π、f1Σ+等5个电子态的光谱数据进行了整理, 并且提出了CN+离子的基态假设, 分析了1Σ+的电子轨道 ((4σ)2(1π)4)以及3Π的电子轨道(4σ)2(1π)4(5σ), 但是仅凭简单的分子轨道理论很难准确的判断CN+离子的基态. 在此之后, Wu[4]通过对C-O离子键长的计算, 提出CN+离子基态为3Π的猜想. 1978年, Shimakura等[5]给出了完整的组态相互作用计算(CI), 使用了最小的Slater类型的轨道, 对于CN+离子的一些低能级电子态进行了研究. 他们发现电子态a1Σ+的能量相较于3Π电子态低0.63 eV, 但是考虑到计算值和实验值之间的差异, 他们并不能认定结论的可靠性, 1979年, Wu[6]运用SCF方法对CN+离子的势能曲线进行了报道, 并给出结论3Π的能量要低于a1Σ+电子态0.33±0.2 eV左右. 同年Hirst[7]提出了电子态a1Σ+和3Π的势能曲线十分接近, 但仍然无法从理论角度给出准确的定论, Murrel[8]等人通过极化CI方法也得出了相同的结论. 1982年, Roos[11]等人采用{6s4p2d}收缩基组, 通过完全活性空间自洽场方法(CASSCF)分别计算了a1Σ+,3Π,3Σ+电子态的势能曲线, CASSCF优化产生的波函数, 基态X1Σ+的能量分别低于3Π,3Σ+, 3600和13000cm-1, 自此确认X1Σ+为CN+离子的基态. 1994年, Hirst[12]对CN+离子的两个离解极限C+(2Pu)+N(4Su)和C+(2Pu)+N(4Du)的所有电子态的势能曲线进行了研究, 采用多组态参考相互作用方法(MRCI)方法计算了电子态的势能曲线, 并给出了部分电子态的永久偶极矩. 1995年, Peterson[13]对不同基组{cc-pV (D,T,Q,5) Z}水平下的X1Σ+,3Π电子态的光谱常数进行了计算与整理. 2002年, Polk等人运用MRCI方法结合AVQZ, AV5Z基组计算了X1Σ+,1Δ,c1Σ+三个电子态的势能曲线, 分别做出了三个电子态在对应振动能级下的偶极矩. 最近, 廖建文[16]等人采用MRCI结合aug-cc-pV5Z基组分别了计算了11Σ+, 21Σ+, 13Σ+, 13Π电子态的势能曲线, 利用MS势能函数拟合的得到了相应的解析函数表达式, 并在此基础上获得了各个电子态的振动和转动能级. 值得一提的是, 对于CN+离子电子态之间的跃迁性质的研究是很少的.
在本文中, 我们对CN+离子的两个解离极限C+(2Pu)+N(2Du)和C+(2Pu)+N(4Su)下的X1Σ+、a3∏、11Δ和A1∏四个电子态的势能曲线进行了研究, 并计算了对应的光谱数据, 永久偶极矩. 同时我们研究了单重态A1∏↔X1Σ+和11Δ↔A1∏之间的跃迁性质, 通过Level8.2[18]软件获得了对应跃迁的弗兰克-康登因子以及辐射寿命.
2 计算方法
本文利用Molpro 2015[19]程序包计算了CN+离子的基态(X1Σ+)以及激发态(a3∏,1Δ, A1∏)的势能曲线. 首先, 采用自旋限制的Hartree-Fork 方法来计算CN+基态X1Σ+的波函数及能量, 以此波函数作为初始波函数, 然后利用CASSCF[20,21]方法对得到的基态波函数进行优化, 最后, 以CASSCF方法优化得到的波函数作为参考, 对其进行多组态相互作用方法计算[22,23], 进而得到相应的势能曲线, 为了提高势能曲线的质量, 在此过程中还加入了Davidson修正[24-26]和三阶 Douglas-Kroll Hamiltonian 近似的标量相对论修正[27, 28]. 由于Molpro程序自身的限制, 计算中使用了其简并对称性C∞v群中的子群C2v,C2v点群中包含4个不可约表示, 分别为A1、B1、B2和A2, 其中C2v群与C∞v群的不可约表示有如下对应关系:Σ+=A1、∏=B1+B2、Δ=A1+A2和∑-=A2. 在计算时, 10个轨道被选为活性空间, 包括6个A1、2个B1和2个B2对称性的分子轨道.
为了得到CN+基态以及低激发态的势能曲线, 对C正离子、N原子均采用AV5Z-DK基组, 对CN+在核间距范围为0.6 Å到6.0 Å之间进行了计算, 步长为0.05 Å. 同时, 为了得到更加光滑的势能曲线, 我们在平衡核间距附近将步长缩短为0.02 Å. 基于得到的势能曲线, 使用Level8.2程序通过求解Schrödinger方程得到各个电子态的光谱常数, 包括平衡核间距Re、振动常数ωe、非谐性常数ωee、激发能Tc和平衡转动常数Bc. 利用上述方法计算得到的光谱常数和MRCI等级下的跃迁偶极矩, 借助Level8.2程序计算得到了A1∏↔X1Σ+和11Δ↔A1∏跃迁的弗兰克-康登因子和辐射寿命.
3 结果与讨论
3.1 光谱常数与势能曲线
采用多参考组态相互作用方法结合AV5Z-DK基组得到了CN+离子的基态以及低激发态的势能曲线, 并将曲线绘于图1中. 由图1可以看出CN+离子的X1Σ+,11Δ,A1∏三个电子态都具有相同的离解极限, 离解极限为C+(2Pu)+N(2Du), a3∏电子态对应的离解极限为C+(2Pu)+N(4Su). 基于得到的势能曲线, 利用Level 8.2[18]程序包计算了电子态的振动能级, 列于表 1中. 同时通过求解分子中核运动的薛定谔方程获得CN+离子的光谱数据, 列于表2中. 从表2中可以看出, 本文计算得到的光谱数据与实验值[3]吻合度很高, 值得一提的是a3∏和1Δ电子态的光谱常数并没有在实验上报道过, 所以为了验证数据的可靠性, 我们列举了已有的理论值[12,13,15,16]作为参考.

图1 X1Σ+、11Δ、A1∏和a3∏电子态的势能曲线Fig.1 Potential energy curves of the X1Σ+, 11Δ, A1∏ and a3∏ states
基于获得的势能曲线, 利用Level8.2程序包, 计算了CN+离子X1Σ+, 11Δ, A1∏和a3∏电子态的全部振动能级, 考虑到篇幅的限制, 本文只列举了各个电子态的前20个振动能级, 根据表 1, 基态X1Σ+的振动能级数位75, a3∏电子态的振动能级数位51, 这与廖建文等人[16]的报道相符, 对于A1∏, 11Δ计算获得的振动能级数分别位69, 66. 目前, 还没有针对这两个电子态的振动能级的实验研究和理论报道.
从表2中可以看出, 对于基态X1Σ+, 本文中的平衡核间距(1.1765 Å)与实验值[3]相差0.038 Å, 误差比为3.2%, 精度高于其他报道的理论值[12,13,15,16]. 同时我们计算出的谐振频率的值为2039.24cm-1, 略高于实验值, 误差为0.2%. 非谐振常数的值为16.31cm-1, 相较于实验值的误差为1%. 转动常数的值为1.8871cm-1与实验值完全相符, 这说明我们计算得到的光谱数据具有很高的可靠性. 激发能并没有相对应的实验值, 所以我们以理论值作为对比, 发现我们得出的离解能的值(7.440eV), 与Polk[15]等人计算的离解能(7.474eV)相差0.074eV, 与廖建文[16]计算的相差0.66eV, 可以看出与之前报道的理论值十分接近.
表1 CN+离子X1Σ+、11Δ、A1∏和a3∏电子态的振动能级(单位cm-1)
Table 1 Vibrational levels for the X1Σ+、11Δ、A1∏ and a3∏ states of CN+ion (in cm-1)

VX1Σ+a3∏A1∏11Δ01010.3621529.4358838.94617658.6313008.3483178.13310470.4018920.6124956.3694810.55412084.2520171.9936879.6036412.93213668.5521390.7148769.4197983.37815221.2922585.83510625.959522.59416742.8223752.56612449.7411030.5918236.2124905.03714253.7612505.7319696.9026022.64816066.8413948.1221126.1527125.38917903.7715356.4922524.7828207.001019608.0816731.0423891.7329261.031120815.3918069.6925227.0030296.861222102.9519372.2726530.5231312.001323265.0520637.7427801.9332303.931424470.8621865.1429041.5833274.671525565.5623053.1430249.3734224.891626715.9224200.6531424.9035155.121727773.4325306.4832568.2936065.221828843.9926369.4433680.1736954.401929893.5427388.4634760.0037823.552030890.2028362.3335808.1238674.03总能级数75516966
对于低激发态a3∏、11Δ, 本文计算得到的平衡核间距分别为1.2478 Å, 1.3755 Å, 与表中的其他理论值较为接近, 谐振频率的值分别为1687.69cm-1和1287.31 cm-1, 非谐振常数的值分别为15.23 cm-1和11.55 cm-1, 值得一提的是我们计算的a3∏谐振频率, 非谐振常数和转动常数与Peterson[13]计算得到的理论值相差较大, 差值为286.19 cm-1、2.03 cm-1和0.2048 cm-1但与其他计算的理论值吻合较好, 与Hirst的差值分别为5.22cm-1、0.02cm-1和0.0138cm-1, 与廖建文的差值分别为26.08 cm-1、0.98cm-1和0.0198cm-1, 所以我们的计算值更加合理.
对于第一激发态A1∏, 本文计算的激发能的值为8020.04 cm-1, 与实验值8141.41 cm-1[3], 相差121.37 cm-1, 但与Hirst[12]的理论值与实验值的差别相比(1981.13 cm-1), 很显然我们的计算值更加精确. 将计算得到的平衡核间距和谐振频率与实验值相比较, 发现我们的计算值均略小于实验值, 误差仅仅为1.6%, 1.3%. 对于非谐振常数和转动常数, 我们的计算值分别为14.69cm-1、1.6631 cm-1与实验数据符合的较好. 同时, 我们也计算了A1∏的离解能(6.346eV), 但没有找到相应的实验值与理论值. 总的来说, 本文计算的光谱数据与实验值和理论值吻合的较好. 说明采用 MRCI/ aug-cc-pV5Z 方法对CN+离子计算是准确可靠的, 可以为后续的研究提供保证.

表2 CN+离子X1Σ+、11Δ、A1∏和a3∏电子态的光谱数据
3.2 永久偶极矩与跃迁偶极矩
图2和图3分别作出了CN+离子永久偶极矩和跃迁偶极矩随着核间距的变化. 从图2 可以看出, 基态和低激发态的永久偶极矩曲线走势相同, 都是先逐渐减小, 然后快速的增加, 这是因为X1Σ+、11Δ、A1∏和a3∏电子态均与C++N离解极限相对应, 表现出相应的离子性质. 基态X1Σ+在平衡核间距处的偶极矩值0.4615a.u., 低激发态1Δ、a3∏和A1∏在各自平衡核间距处的偶极矩值分别为0.1197a.u.、0.6867a.u.和0.8082a.u. 将我们的计算数据与Hirst[12]首次报道的理论值相比较, 本文的结果与理论值几乎一致, 这保证了我们计算结果的合理性.
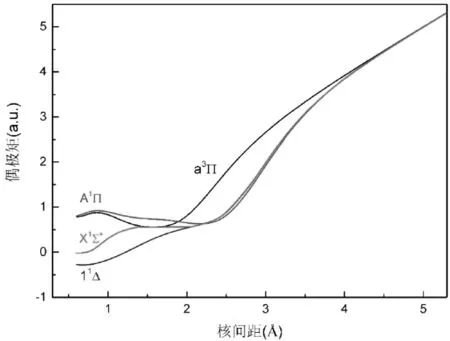
图2 X1Σ+, 11Δ,A1∏和a3∏电子态的永久偶极矩Fig.2 Permanent dipole moments of the X1Σ+, 11Δ,A1∏ and a3 states
跃迁偶极矩对于计算爱因斯坦因子是必不可少的. 根据图3可以发现A1∏↔X1Σ+跃迁的跃迁偶极矩随着核间距的增大而增大, 当核间距达到 1.05 Å 时, 跃迁偶极矩的值达到最大值将不再增加而是缓慢的减小. 最后, 当核间距在3.0 Å附近, 跃迁偶极矩趋向于 0, 这是由于原子范围内轨道禁止跃迁引起的. 对于11Δ↔A1∏跃迁, 跃迁偶极矩随着核间距的增大而减小, 在核间距达到1.1 Å 时, 达到最小值(-0.2585a.u.), 接着不再减小, 随着核间距的增大逐渐上升直至0.

图3 A1∏↔X1Σ+和11Δ↔A1∏跃迁的跃迁偶极矩Fig.3 Transition dipole moments of the A1∏↔X1Σ+ and 11Δ↔A1∏ transition
3.3 跃迁性质
FCF反映的是两个振动波函数的重叠程度, 表示电子态振动能级之间的跃迁几率. 我们运用修正后的势能曲线以及A1∏↔X1Σ+和11Δ↔A1∏跃迁的跃迁偶极矩, 借助于 Level 8.2 程序, 计算出在不同振动能级下的跃迁的FCF. 将振动量子数在0到4之间所有可能产生的 FCF 都画在图 4和图5中, 更加直观地展示了A1∏↔X1Σ+和11Δ↔A1∏跃迁的 FCF 分布. 同时对应跃迁的FCF以及辐射寿命τ被列在表3中.

图 4 CN+离子的前4个振动能级下X1Σ+↔A1∏跃迁的 FCFs 柱形图Fig.4 FCFs of CN+ for the lowest four vibrational levels of the X1Σ+↔A1∏ transition
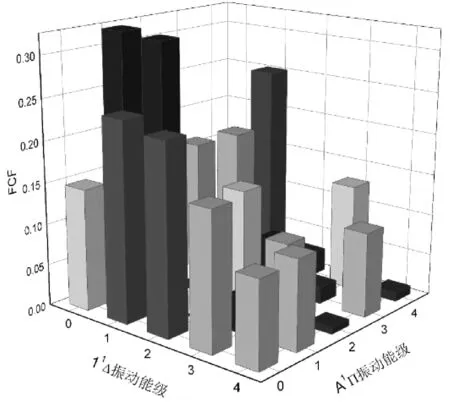
图 5 CN+离子的前4个振动能级下11Δ↔A1∏跃迁的 FCFs 柱形图Fig.5 FCFs of CN+ for the lowest four vibrational levels of the 11Δ↔A1∏ transition
考虑到制备超冷分子的可能性, 我们借助Level8.2[18]程序包计算了不同振动能级下的A1∏↔X1Σ+和11Δ↔A1∏跃迁的FCF, 并将对应的FCF列在表3中, 由表3可以看出A1∏(v′=0,1)↔X1Σ+(v=0)的FCF分别为0.3639, 0.3634, 11Δ(v′=0,1)↔A1∏(v=0)的分别为0.1473, 0.2400. 不幸的是, 很显然A1∏↔X1Σ+和11Δ↔A1∏跃迁在不同振动能级下的FCF都是很小的, 并不满足分子激光冷却的首要条件(具备高度对角化的FCF). 同时, 基于计算出的FCF和跃迁偶极矩(TDMs)结合以下公式[29, 30], 我们给出了跃迁的辐射寿命.
(1)
公式中, 爱因斯坦系数的单位为s-1, M(r)为单位为D的跃迁偶极函数,v为辐射频率, 单位为cm-1,S(J′,J″)为转动强度因子,Ψv′,J′和Ψv″,J″为归一化的径向波函数. 从表2中可以看出无论A1∏↔X1Σ+和11Δ↔A1∏都不具备足够短的辐射寿命(10-6-10-8), 这表示并不能提供足够的激光冷却循环速率来产生自发辐射力.
综上所述, 对于CN+离子的A1∏↔X1Σ+和11Δ↔A1∏单重态跃迁, 并不具备激光冷却的可能性.
4 结 论
采用多组态参考相互作用方法(MRCI), 结合AV5Z-DK基组计算得到CN+离子X1Σ+, 1Δ, A1∏和a3∏电子态的势能曲线, 考虑到数据的准确性, 在计算中考虑了Davidson修正, 核价相关修正、标量相对论效应和三阶Douglas-Kroll Hamiltonian近似的标量相对论修正. 基于获得的势能曲线, 利用Level8.2程序包求得了各电子态的振动能级, 同时拟合得到了对应电子态的光谱常数, 通过与实验值和现有的理论值的比较, 验证了计算结果的合理性. 在此基础上, 还对CN+离子电子态的永久偶极矩和跃迁偶极矩进行了研究.
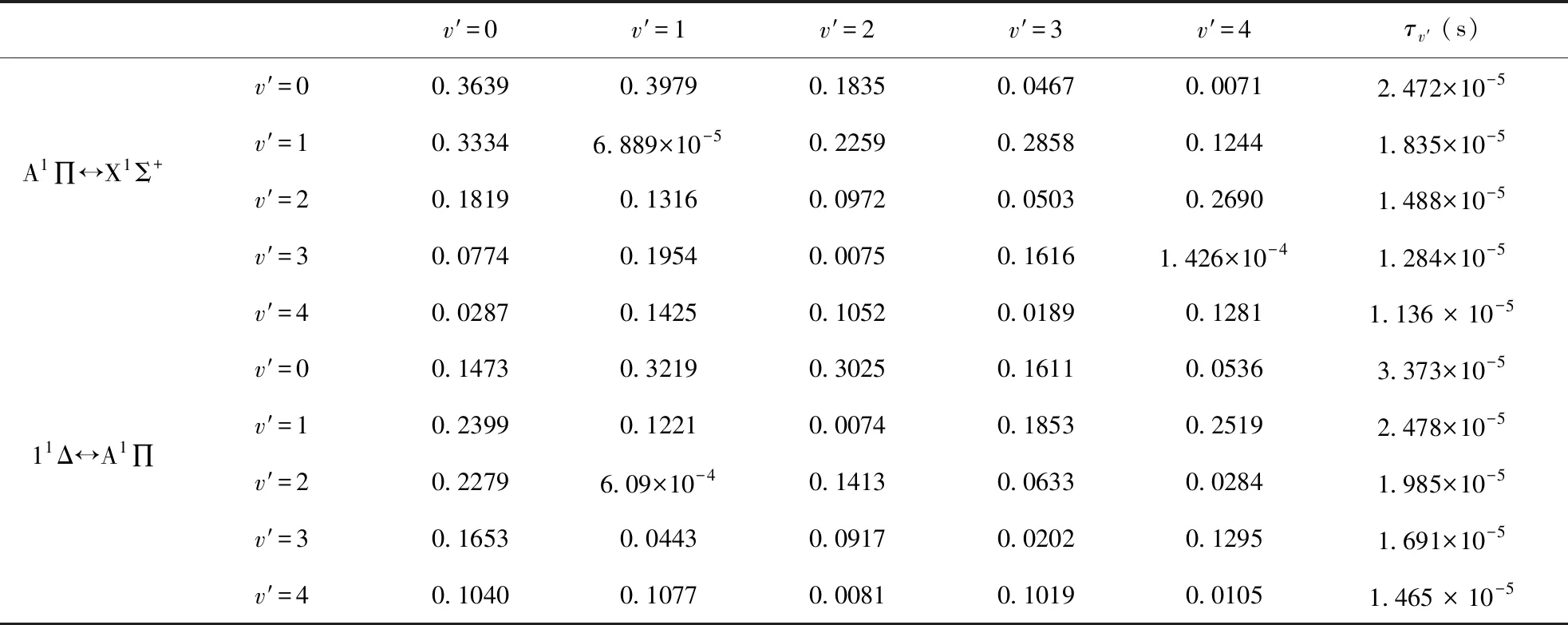
表3 A1∏↔X1Σ+和11Δ↔A1∏跃迁的FCF和辐射寿命τ
根据计算得到的永久偶极矩和跃迁偶极矩, 对A1∏↔X1Σ+, 11Δ↔A1∏跃迁的跃迁性质进行了分析, 通过对应跃迁在不同振动能级下的FCF及辐射寿命, 发现对于CN+离子的A1∏↔X1Σ+和11Δ↔A1∏单重态跃迁, 并不具备激光冷却的可行性.
