危害性矩阵分析方法关键问题研究

2019-04-29郝恒曹海斌张康杜一凡

海军航空大学学报 2019年1期

郝恒，曹海斌，张康，杜一凡

（中国船舶科学研究中心深海载人装备国家重点实验室，江苏无锡214082）

故障模式、影响及危害性分析（Failure Mode，Effect and Criticality Analysis，FMECA）是航空、航天、武器等装备可靠性设计过程中普遍采用的一种故障分析方法。FMECA包括故障模式及影响分析（FMEA）和危害性分析（CA）。

FMEA属于定性分析，目前已发展的比较完善，参照GJB/Z 1391[1]及相关教材[2-3]能够顺利开展并取得良好效果。

CA进行故障模式风险评价和排序，也已得到广泛应用，目前针对CA方法的文献[4-7]主要集中在采用模糊数学的方法进行危害性评价，而针对航空、航天、舰船等重大装备领域常用的危害性矩阵分析方法，可能由于技术保密等原因，现有的FMECA指导标准[1]、可靠性工程手册[8]和文献[9-10]关于危害性矩阵方法的内容只给出分析原理及流程，示例仅给出最终结果，缺乏斜率取值、纵横坐标划分、非单点故障情况等关键问题的处理过程，造成设计人员在进行装备故障模式危害性矩阵分析时缺乏指导文件，出现分析困难、甚至分析结果不合理等问题。同时，采用手工绘图的方式使得分析效率和精度都比较低。

针对以上危害性矩阵方法在使用中的困难，本文对矩阵斜率取值、坐标划分、单点与非单点故障处理、危害度与危害性等关键问题进行研究，推导出危害性定量计算式，并以某型军机升降舵操纵分系统为例，给出分析实例。

1 危害性矩阵分析方法

1.1 绘制危害性矩阵图

绘制方法[11]：横坐标一般按等距离表示严酷度等级，纵坐标为产品危害度Cr或故障模式危害度Cm,j或故障概率发生等级（定性分析时），见图1。首先，按Cr值或Cm,j值在纵坐标上查到对应的点，再在横坐标上选取代表其严酷度类型的区间，并在区间内标注产品或故障模式的位置（利用产品或故障模式代码标注），从而构成产品或故障模式的危害性矩阵图。在产品设计初期不能获取产品的故障数据时，一般绘制定性危害性矩阵，故障概率发生等级一般分为5个等级，即A、B、C、D、E。

图1 危害性矩阵图Fig.1 Criticality matrix

产品第j个故障模式危害度Cm,j计算公式为：[12]式（1）中：αj为故障模式频数比；βj为故障影响概率，是产品在某故障模式发生的条件下，其最终影响导致“初始约定层次”出现某严酷度等级的条件概率[13]；λp为被分析产品在其任务阶段内的故障率（1/h）；t为产品任务阶段的工作时间（h）。

当产品获得的故障数据为任务阶段某一故障模式的故障率λm,j或故障模式的发生概率Pm,j，故障模式危害度Cm,j还可以表示为：

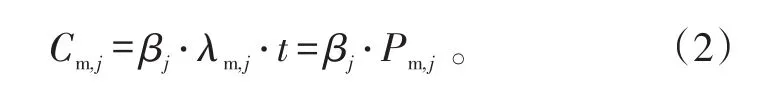
产品的危害度Cr是该产品在给定严酷度类别下的各种故障模式危害度Cm,j之和，即

式（3）中，N为该产品在相应严酷度类别下的故障模式总数。

应针对每一严酷度分别计算产品在该严酷度下的产品的危害度，记为Cr（Ⅰ）、Cr（Ⅱ）等，不同严酷度下的故障模式危害度Cm,j不能相加。

1.2 危害性矩阵图的应用

从图1标记的故障模式分布点向对角线（虚线OP）作垂线，以该垂线与对角线的交点到原点的距离作为度量故障模式（或产品）危害性的依据，距离越长，其危害性越大，越应尽快采取改进措施。在图1中，因O1距离比O2距离长，则故障模式M1比故障模式M2的危害性大。

2 危害性矩阵方法应用时的困难

目前，危害性矩阵应用时存在以下困难：

1）危害性矩阵图对角线斜率大小影响故障模式（或产品）危害性的分析结果，但现有资料没有给出对角线斜率的选取方法或建议值，使得绘制矩阵图时缺少指导依据和参考标准。

2）现有资料给出了矩阵图横坐标为严酷度、纵坐标为危害度，但没有给出坐标值标注方法或推荐的作图比例，给出的示例中危害度大多采用等比例标注，合理性有待验证。

3）危害性矩阵图需手工绘制，工作量很大，且精度比较低，故障模式较多时垂线绘制困难且难以分辨；产品设计状态的更新时，危害性矩阵图也应进行更新，多数情况下需重新绘制，效率比较低。

4）由于没有统一的绘图标准，不同系统的故障模式危害性由各系统设计师绘制在不同的矩阵图中，系统之间危害性大小难以比较。

5）危害性矩阵分析过程中非单点故障的处理、危害度计算所涉及相关参数的概念理解与取值等问题也存在一定难度，缺少详细解读资料。

3 危害性矩阵分析方法关键问题研究

本节对危害性矩阵斜率确定、纵横坐标划分、单点故障与非单点故障的处理、危害度和危害性定量计算等问题进行研究，用以解决危害性矩阵分析方法在应用时存在的困难。

3.1 对角线斜率与坐标划分

危害性矩阵对角线的斜率大小直接影响故障模式分布点向对角线所作垂线与对角线的交点位置。如图2所示，对角线斜率k=1时，故障模式M1的危害性大于故障模式M2的危害性，对角线斜率k=0.75时，故障模式M1的危害性显然又小于故障模式M2的危害性，所以危害性矩阵对角线斜率的取值直接影响危害性分析结果。

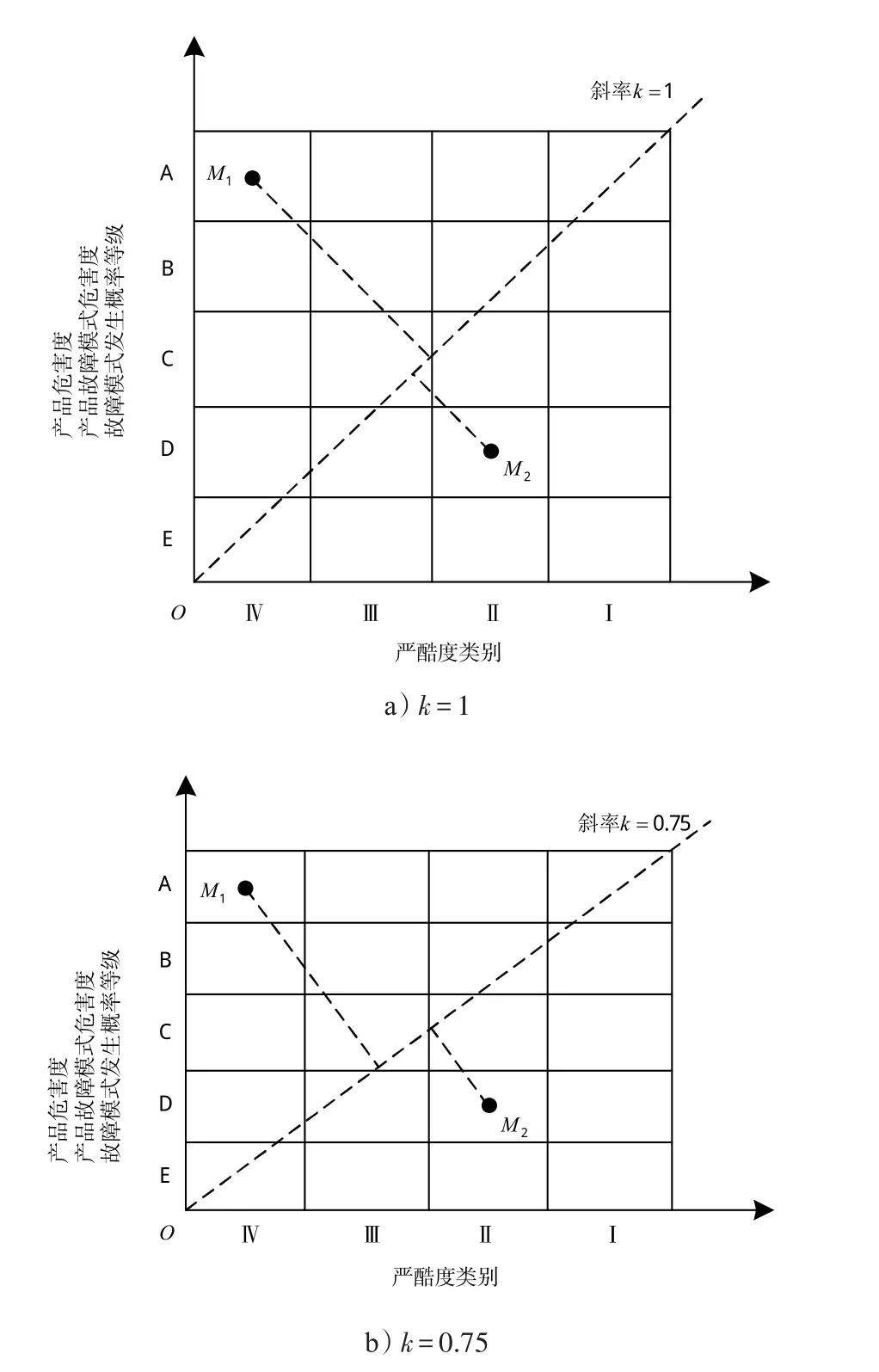
图2 不同斜率的危害性矩阵图Fig.2 Criticality matrix with different slope

危害性矩阵的坐标划分影响故障模式点在矩阵图中的位置，从而影响故障模式危害性分析结果。

危害性矩阵斜率与坐标划分是相互关联的，斜率一旦确定，可以通过调整坐标获得合理的分析结果，若先划分好坐标，也可以通过调整斜率值得到合理的分析结果。

本文采用先确定斜率再划分坐标的方法绘制危害性矩阵图。文献[11]进行某型飞机升降舵操纵分系统危害性分析时，危害性矩阵斜率为1，文献[14-15]虽没有明确指出危害性矩阵斜率值，但根据矩阵图可以观察出，其斜率值都在1附近。且斜率为1时便于绘图、所绘图形美观，故确定危害性矩阵斜率为1。

危害性矩阵横坐标划分明确，通常分为4类严酷度，等距离划分。纵坐标划分目前很多文献[3，8-9]采用等比例坐标，即纵坐标值大小与其距原点的距离成正比，如图3所示。这种纵坐标划分方式存在以下缺点。

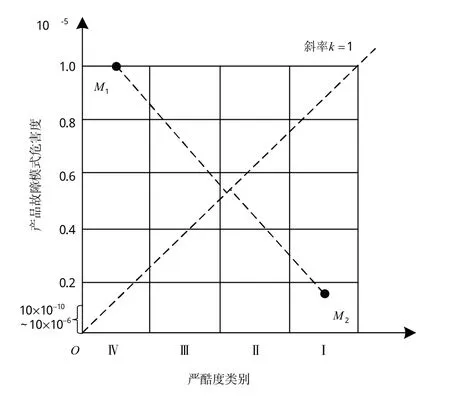
图3 等比例坐标划分的危害性矩阵图Fig.3 Criticality matrix with isometric coordinates

1）纵坐标等比例划分方式在航空、航天、舰船等特别重视安全性的领域缺乏合理性。图3中，危害度为1.0×10-5的Ⅳ类故障模式M1的危害性与危害度为0.15×10-5的Ⅰ类故障模式M2的危害性几乎相等。根据矩阵图，应对故障模式M1和M2的风险做出同时接受，或同时拒绝的结论。但在军用航空、航天和舰船领域，Ⅰ类故障模式可接受的危害度[16]一般小于1.0×10-6，Ⅳ类故障模式可接受的危害度[16]一般小于1.0×10-1，所以故障模式M1的风险是可以接受的，故障模式M2的风险是不可以接受的。由此可以看出，等比例划分纵坐标的方式在这些领域是不合适的。

2）复杂装备的故障模式危害度分散在1.0×10-10～0.1各个区间，图3纵坐标仅画出了0～1.0×10-5部分，若要等比例画出1.0×10-10～0.1的纵坐标，1.0×0-5～0.1部分会使纵轴变长1万倍，1.0×10-10～1.0×10-6部分则集中在图3纵轴1/2个坐标间距内，难以区分。

鉴于等比例坐标的缺点，推荐纵坐标采用对数坐标，文献[11]中绘制的危害性矩阵图纵坐标采用的便是对数坐标。

纵坐标采用对数坐标的危害性矩阵做法如下：纵轴等距分为n段，从原点向纵轴正方向，第1个坐标为10-x（10-x小于Ⅰ类故障模式最大可接受严酷度），后续坐标点坐标值依次为10-x+1、10-x+2、10-x+3、…。坐标间距及具体坐标值一般参考产品的严酷度定义和风险接受准则[17]来确定。以军品为例进行对数坐标标注，军用飞机、舰船和武器装备发生Ⅰ类故障模式的可接受危害度一般小于1.0×10-6，Ⅳ类故障模式的可接受危害度一般小于1.0×10-1。因此，认为危害度为10-6的Ⅰ类故障模式与10-1的Ⅳ类故障模式危害性相同，故在合适位置作出对角线的一条垂线，在垂线上找到Ⅰ类故障模式点M2和Ⅳ类故障模式点M1，M2对应的纵坐标值即为10-6，M1对应的纵坐标值即为10-1，10-1～10-6之间纵轴等分为5段，按照对数坐标标注。10-6坐标点与原点之间建议距离为2个坐标间隔，因为小于10-8的危害度已经很小，其危害性都属于可接受范围，可将故障模式点标注在10-8位置上。采用对数坐标系的军用产品危害性矩阵如图4所示。

图4 纵坐标为对数坐标系的危害性矩阵图Fig.4 Criticality matrix with logarithmic coordinates of Y-axis

3.2 单点故障与非单点故障分析

单点故障[18]与非单点故障在危害性分析时的区别在于危害度计算，具体又体现在故障影响概率βj的取值。

1）单点故障分析。有人认为单点故障的故障影响概率βj=1，即单点故障一旦发生就一定会造成系统故障，并导致的故障影响概率为100%。这种观点不完全正确，单点故障一旦发生就会导致系统故障是正确的，但系统故障导致的影响可能有多种，所以βj不一定为1。如飞机升降舵轴承滚珠掉出就会导致升降舵丧失操纵功能，但轻度影响为影响飞机操控，增大机组负担，最坏影响会导致飞机操纵失效，撞上障碍物，导致人员伤亡。因此，对于单点故障，仍然要仔细分析某一故障模式可能产生的多种影响，并根据统计经验或标准推荐值确定每一种最终故障影响的百分比，即βj。

2）非单点故障分析。非单点故障，即某个部件或设备存在备份设计，分析其故障影响时必须考虑备份设计的存在。当发生故障时，该故障模式对系统或产品造成的影响至少可以分成2种情况。第1种情况是故障模式发生后，备份设计正常启动，这种情况下对系统或产品造成的影响假设为E1，故障影响概率为β1；第2种情况是故障模式发生后，备份设计未能正常启动，这种情况下对系统或产品造成的影响假设为E2，故障影响概率为β2。显然E2的严酷度要高于或等于E1。假设备份设计未能正常启动概率P1，则β2=P1，β1=1-P1。

稍微复杂的情况为，存在备份设计的某部件发生故障后，在不考虑备份设计时，其故障影响就存在多种，假设为E1、E2，对应故障影响概率为P1、P2（P1+P2=1），备份设计未能正常启动概率P3，最终影响为以下3种：

1）故障模式发生后，备份设计未能正常启动，导致影响E1，故障影响概率β1=P1P3。

2）故障模式发生后，备份设计未能正常启动，导致影响E2，故障影响概率β2=P2P3。

3）故障模式发生后，备份设计正常启动，导致影响E3，故障影响概率β3=1-P3。

3.3 故障模式危害性定量计算式

鉴于第2节所述手工作图的缺点，推导故障模式危害性定量计算公式。

设危害性矩阵图对角线斜率为k，故障模式点坐标为M(xm,ym)，过点M做对角线的垂线，垂足为N(xn,yn)，如图5所示。故障模式M的危害性可以用垂足点N与原点O之间的距离表示，即

由数学知识分析可得，垂足N的坐标。

代入上式，得到：

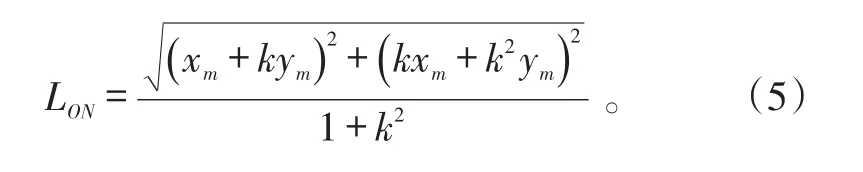
图5 故障模式危害性定量计算分析图Fig.5 Quantitative calculation chart of failure mode criticality

因此，危害性矩阵对角线斜率为k，故障模式点的坐标为(x,y)时的故障模式危害性为：

x、y并非直接采用严酷度等级和危害度数值，而需要对其进行坐标数值转化。转化时，可以借助绘制的危害性矩阵，参考以下几项原则：

1）转化后的坐标是等比例标注的，且横、纵坐标比例尺相同；

2）转化后的Ⅳ、Ⅲ、Ⅱ、Ⅰ类严酷度坐标值依次为s、2s、3s、4s，s可为任意正数；

3）设Ⅰ类故障最高可接受危害度为10-a，Ⅳ类故障最高可接受危害度为10-b，危害度10-b的Ⅰ类故障模式点在对角线上；

4）危害度为10-a的Ⅰ类故障模式与危害度为10-b的Ⅳ类故障模式危害性相等，即2点连线与对角线斜率垂直；

5）故障模式危害度Cm＜10-a-2时，故障模式危害度Cm可以视作10-a-2。

根据以上原则，可以列出以下坐标变化关系：

参数A和B满足方程：

求解可得：

整理后坐标变化关系为：

进行危害性定量计算时，首先，通过式（11）～（12）计算得到故障模式坐标转化后的坐标值(x,y)；最后，通过式（6）计算得到故障模式危害性数值。

3.4 危害度与危害性

由式（1）可以看出，危害度为产品故障率或故障概率与一系列系数的乘积，本质上还是一个概率量，表示产品发生故障并造成某种影响的可能性。而危害性是故障严酷度与故障发生可能性的综合度量，是故障带来的风险。实际工作中有些人会将危害度与危害性的概念混淆。

同一产品同一严酷度下的故障模式危害度可以相加，得到产品特定严酷度下的产品危害度，相加时不区分产品故障模式。通过产品危害度可以绘图或计算得到产品危害性，并对产品危害性进行排序，危害性大于某一规定数值的产品即可确定为装备的可靠性关键重要产品，以便在设计、生产、使用中进行控制。

文献[11]认为产品的危害性数值等于各部件、零件危害性数值相加，这不恰当。由式（6）、（11）～（12）可知，危害性与危害度之间存在数值关系，但不是简单的比例关系，因而危害性数值大小只表达危害性的相对关系，即危害性数值为20的故障模式的危害性大于危害性数值为10的故障模式危害性，但危害性并不是其2倍。

因此，产品的危害性数值不等于各零部件危害性数值相加，零部件危害性也不等于零部件各故障模式危害性相加。

产品的危害性应先计算得到产品危害度，再通过产品危害度计算得到产品危害性。

4 定量危害性矩阵分析示例

以某军机升降舵操纵分系统[1]为例，进行定量危害性矩阵分析。升降舵操纵分系统的功能是保证飞机的纵向操纵性，由安定面支承、轴承组件、扭力臂组件、操纵组件、配重组件和调整片组成。

该军机Ⅰ类故障模式可接受危害度为1.0×10-6，Ⅳ类故障模式可接受危害度为1.0×10-1，以对角线斜率k=1绘制危害性矩阵图，纵坐标采用对数坐标，危害性矩阵如图4所示。

危害性定量计算的坐标转化参数：坐标转化公式为：

故障模式危害性定量计算式为：

应用式（13）～（14），可以定量计算升降舵操纵分系统各故障模式的危害性。该军机升降舵操纵分系统定量危害性分析结果如表1所示，限于篇幅仅展示部分结果。

从分析结果可以看出，升降舵操纵分系统故障模式危害性数值全部集中在9～19范围内，手工绘图绘制难度较大，且有些值难以区分，甚至会出现排序相反的情况。而借助本文中的计算方法，则可以很容易地进行精确排序。

调整片电动效应机构不工作危害性最大，为18.803，轴承组件滚珠掉出危害性次之，为18.562，两者都可能造成Ⅰ类事故，危及飞机安全。根据“军机Ⅰ类故障模式可接受危害度为1.0×10-6”，可以计算得到可接受故障模式危害性值为17.677 8，即故障模式危害性值大于17.677 8的均不满足风险要求，应采取设计改进或使用补偿措施降低其故障模式危害性。

操纵组件摇臂间隙过大、连杆间隙过大和支架裂纹3个故障模式均为Ⅲ类严酷度，若将其危害性数值直接相加，则操纵组件Ⅲ类故障危害性高达25.111，而采用式（3）先计算产品危害度再计算产品危害性的方法，得到操纵组件Ⅲ类故障危害性只有9.408 6，验证了“产品危害性值由零部件危害性值或故障模式危害性值直接相加”的说法是不合适的。