制导火箭弹起控时间对规划弹道的影响

2019-04-29贾晓玲田晓丽范旭朱豪坤王春柳

海军航空大学学报 2019年1期

贾晓玲，田晓丽，范旭，朱豪坤，王春柳

（1.中北大学机电工程学院，太原030051；2.辽沈工业集团有限公司，沈阳110045）

制导火箭弹是一种介于普通弹箭和导弹之间的弹箭，是普通弹药与现代高新技术相结合的典范，具有射击精度高、成本较低的特点。目前，弹箭上的制导执行机构大体分为3类：阻力器、脉冲发动机、鸭舵。其中，鸭舵执行机构以其驱动灵活适应能力强的特点受到国内外科研工作者的青睐[1]。制导火箭弹在中制导阶段[2]结束后，弹箭需通过基准弹道预先确定的空间坐标并具有利于末制导控制阶段的速度矢量方向。但弹箭实际飞行弹道在发动机推力偏心、横风等扰动因素作用下会产生未知的弹道偏差，不能与预先设定的基准弹道重合[3]。因此，研究制导火箭弹中制导段弹道的规划问题十分必要。文献[4]概述了多种常见轨迹优化方法的算法、特点、应用以及未来的发展趋势；文献[5]研究了Gauss伪谱法在多级固体运载火箭上升段轨迹快速优化设计中的应用；文献[6]侧重对滑翔型制导炸弹的最大射程优化问题进行探讨；文献[7]研究了弹箭最大末速随射程的变化规律。但国内外对弹道规划影响因素方面的研究较少。本文建立了考虑飞行过程中弹箭能量损失大小的弹道规划问题最优控制模型，通过高斯伪谱法仿真验证，对影响中制导阶段制导火箭弹末速的因素进行研究。

1 火箭弹弹道规划计算模型的建立

1.1 状态方程

由于求解最优控制问题的过程中迭代次数较多，计算时间较长，故弹箭运动状态方程不应太复杂[2]，在不影响求解精度前提下作如下简化：

1）文中弹箭系尾翼式火箭弹，出炮口时转速极低，因而不考虑滚转的影响；

2）中制导阶段规划弹道的计算与火箭弹实时姿态无太大关系，相应简化；

3）不考虑地球曲率及自转对弹箭飞行过程的影响。

得到有控制点弹道方程为[1]：

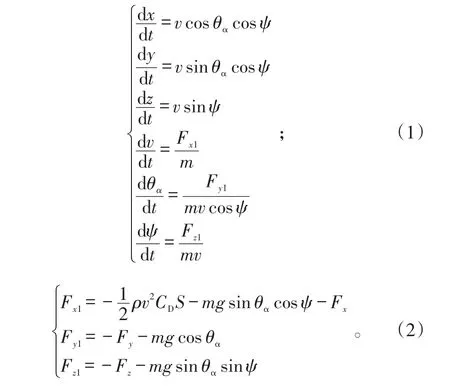
式

（1）、（2）中：x为射程；y为弹箭飞行高度；z为弹箭偏航距离；v为弹箭相对于空气的速度；θα为方向角；ψ为高低角；ρ为空气密度；m为弹箭质量；CD为攻角为零时的摩阻系数；S为弹箭参考面积；g为重力加速度；Fx为控制力附带的阻力增值；Fy为舵面偏转引起的纵向可控力；Fz为舵面偏转引起的侧向可控力。

由舵面产生的控制力F满足：式（3）中：Cδ为舵偏角修正系数；Q为动压；SW为舵翼面积。

飞行力学中常利用过载n评定弹箭的机动性[8]。将有控弹道方程（1）中由舵面产生的可控力F修改为过载n，两者满足：

从而得到如下弹箭运动状态方程：

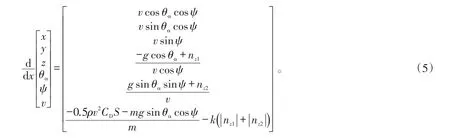
式（5）中，nz1、nz2分别为纵向过载和横向过载，即控制变量。

1.2 代价函数

弹箭在中制导阶段依靠主动段终点获得的能量飞向目标，并且部分机械能用于克服空气阻力作了功。为在末制导阶段开始时保留较大的弹箭末速，代价函数取为动能损失最小，即：

式（6）中：v0为弹箭中制导阶段起始速度；vf为中制导阶段末速度。

1.3 控制约束与边界条件

弹箭在空中飞行时，由舵面产生的过载存在其上限[1]。有：

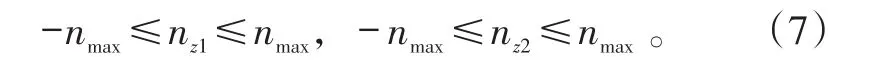
式中，nmax为舵面提供过载上限。

弹道优化问题的初始约束表示为：

式（8）中，下标为0的参量是弹道规划过程开始时给定的初始值，分别对应式（1）中各参量。

终值约束表示为：

式（9）中，下标为f的参量是弹道规划过程结束时的终端值，分别对应式（1）中各参量。

优化过程末速度v(tf)及所需时间tf无法预判，自由取值。

2 高斯伪谱法

高斯伪谱方法对于求解非线性最优控制问题具有良好的收敛性和较低的初值敏感度，且计算量低、精度高，受到众多国内外学者的推崇[5]。

2.1 时域变换

最优控制问题的系统运动时间区域为[t0,tf，t0]表示初始时刻，tf表示终端时刻，高斯伪谱法将时间区间进行无量纲化转换到[-1,1]区间，并对系统时间t作如下变换：

无量纲化变换后的变量可通过构造PK(τ)插值多项式近似：

式（11）的根即Legendre-Gauss（LG）点。记K阶LG点的集合为κ。Gauss伪谱法通过LG点和τ0=-1构造离散节点，记节点组成的集合为κ0，以K+1个拉格朗日插值多项式Li(τ)为基函数来近似状态变量内的时间因素，即：

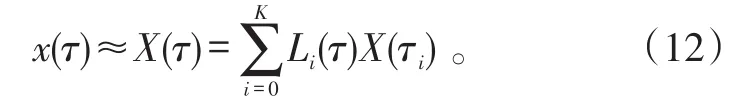
式（12）中：

2.2 终端状态约束离散

根据动力学方程有：

式(15)包含的积分因子可近似为高斯积分形式：

2.3 方程约束离散

状态量微分形式可通过对拉格朗日插值多项式求导近似得到，进而复杂的微分方程求解过程可近似为代数求解，即：

微分矩阵D由下式确定：

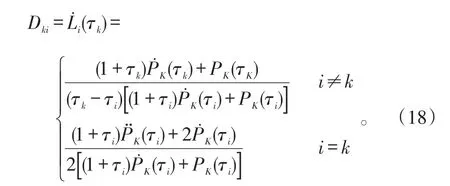
式（18）中：τk为集合κ中的点；τi属于集合κ0。

2.4 代价函数离散

对代价函数式（6）基于Gauss积分进行近似，得到的近似代价函数如下：

式（19）中：Φ为非积分项指标；g为积分项指标的被积分项。

2.5 优化求解模型建立

通过以上数学变换可将文中弹道规划问题描述为：首先，将系统运动时间区间[t0,tf]无量纲化；其次，确定离散点上的状态变量和控制变量；最后，解算出终端时刻，并使代价函数（19）最小。优化过程参量应满足初始状态约束和终端状态约束，分别为：

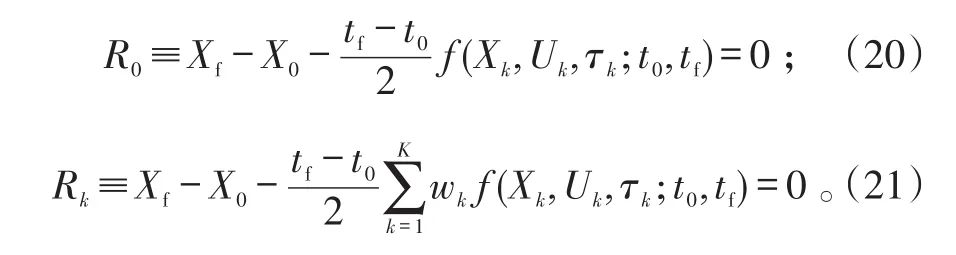
式（20）、（21）中，k=1,2,…,K。

边界条件和路径约束分别为：

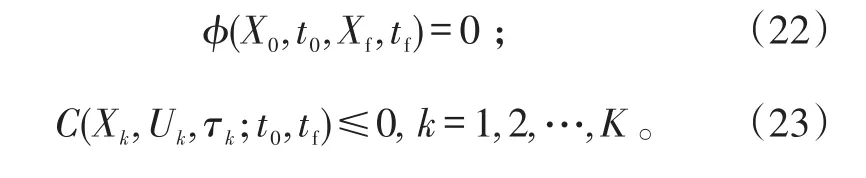
3 弹道仿真与分析

3.1 边界条件选取

某型制导火箭弹相关参数为：弹重m=57kg，参考面积S=0.047 m2，舵面积Sw=0.003 2 m2。动力飞行段在2 s左右，测量装置和计算装置对规划弹道初始数据的实时测算在4 s左右。因此，启动弹箭执行装置应在6 s之后[2]。依据在标准状态下计算6D弹道微分方程得到的理想弹道可知，火箭弹在大约37 s时到达弹道最大高度。弹道规划起控时刻及对应的弹道各项初始参数如表1、图1所示。

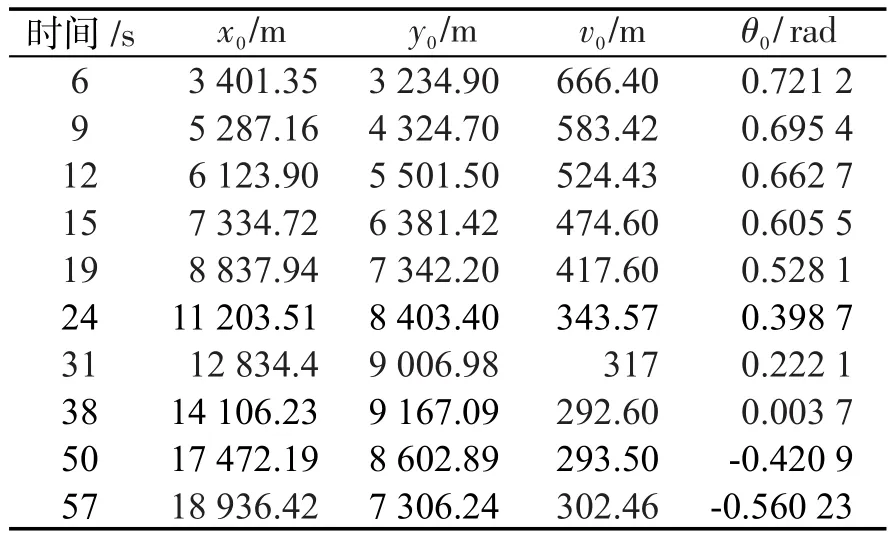
表1 弹道规划起控时刻及各项初始参数Tab.1 Start-up time and initial parameters of trajectory planning

图1 弹道规划起控时刻对应弹道位置Fig.1 Trajectory position corresponding to the control time of trajectory planning

弹道爬升段起控点设置较多，因为弹箭在此阶段运动历程尚短，弹箭机械能克服外界阻力损耗较少，故此阶段出现最佳起控点的概率较大。而弹箭运动至弹道下降段时，一方面总能量损耗渐大，另一方面弹箭相距目标位置点越来越近，弹道规划过程为满足终端约束条件，须要舵面提供较大的控制过载，从而间接增大了弹箭飞行阻力，减小弹箭抵达目标位置点时的速度。

弹道规划终端条件约束如表2所示。

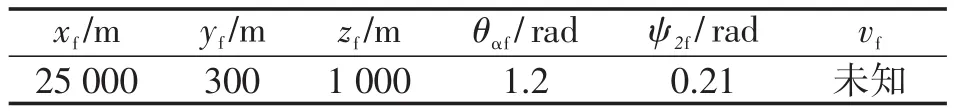
表2 终值条件Tab.2 Terminal numerical conditions

3.2 仿真结果分析

在仿真规划弹道中选取6 s起控（基准弹道初始阶段）、24 s起控（基准弹道中段）、57 s起控（基准弹道末阶段）这3条代表性的弹道进行分析，分别如图2～5所示。

图2 不同起控时间对应飞行距离曲线Fig.2 Flight distance curve corresponding to different start-up time

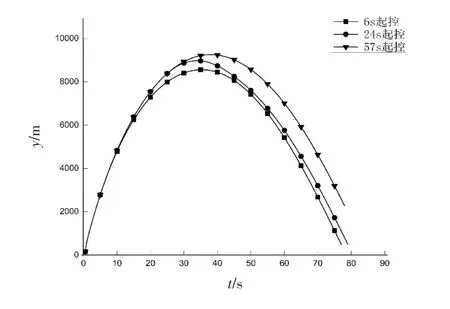
图3 不同起控时间对应弹道高度曲线Fig.3 Trajectory altitude curve corresponding to different start-up time

图4 不同起控时间对应偏航距离曲线Fig.4 Yaw distance curve corresponding to different start-up time

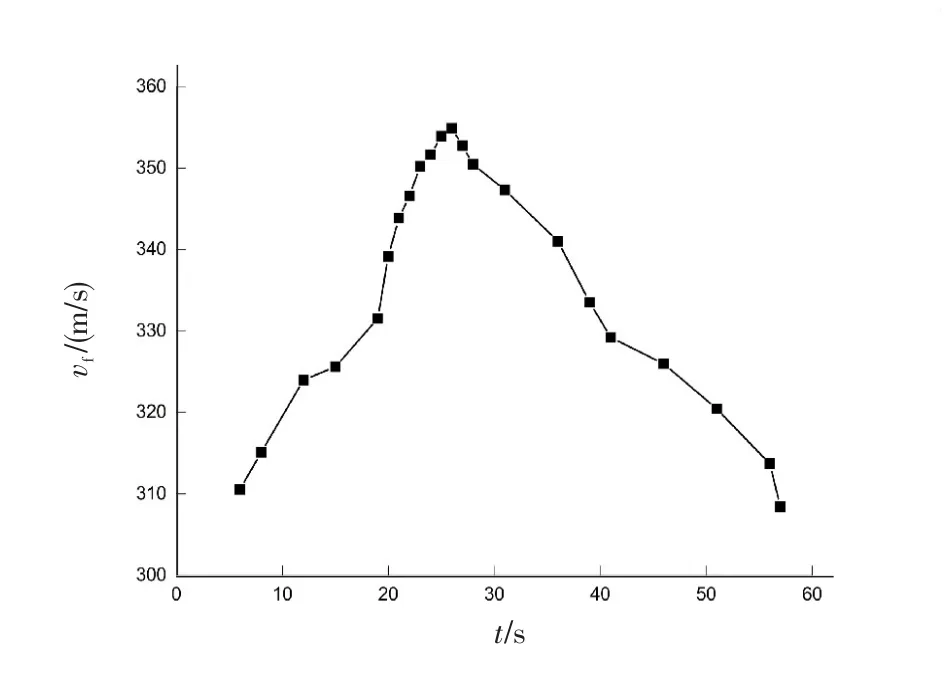
图5 不同起控时间对应规划弹道末速度Fig.5 Planned terminal trajectory velocity corresponding to different start-up time

分析图2可知，弹箭起控时间越早，到达规划弹道有效射程所需的时间越短；分析图3可知，弹箭起控时间过早对规划弹道目标高度影响较大，而在标准弹道顶点附近及之后起控对规划弹道目标高度几乎没有影响；分析图4可知，6 s起控时偏航弹道会发生较大曲折，原因是弹箭必须通过多余的位移和控制过载来同时达到规划弹道终点的三坐标分量终值；57 s起控时会出现无法到达预定目标位置的情况，原因是弹道规划时间太短，到达目标位置需要的控制过载量过大，已超出弹箭能提供的过载上限；而24 s起控时对应的对应的偏航弹道相对平滑，弹道斜率（即速度矢量）始终为正且维持在较小的变化范围内，说明此时起控控制过载变化较小，弹箭的飞行稳定性可以得到有效保证。

分析图5可知，弹道规划起始时刻在27 s左右时，弹箭到达预定目标位置点末速度最大，偏早或偏晚起控都会导致末速度有所削减，最多可使末速度减小11%左右。

在靶场试验中，用相控阵雷达对5发制导火箭弹在射程25km处的末速进行了测量，第1发作为基准弹道，末速为358.4 m/s，其余4发以仿真计算中末速最大对应的27 s为起控点，末速分别为347.9 m/s、350.2 m/s、349.2 m/s、356.7 m/s，误差范围在3%以内，验证了仿真计算的正确性。