飞行甲板多机滑行路径规划
2019-04-29贺少华颜世伟许景伟
贺少华,颜世伟,许景伟
(1.海军研究院,北京100161;2.海军试飞大队,辽宁兴城125100)
合理保障舰载机,对提高航母战斗力具有重要的意义[1]。舰载机起降任务规划是一类优化与决策问题。飞行甲板调运空间狭窄且调运任务种类繁多,各种时间、空间和资源约束条件复杂,再加上舰载机的起飞和回收方式与陆基飞机相比有所不同,使得任务规划问题存在特殊性,须要根据起降任务的特点建立相应的数学模型,设计优化指标和制定决策方案,保证舰载机安全高效地完成任务。另外,由于起降任务规划的复杂性,需要综合运用控制理论、飞行力学、运筹学、人工智能等学科的知识,才能在建立数学模型和设计优化算法的过程中准确地对具体问题进行描述和提炼。因此,研究舰载机起降任务规划问题是多学科知识的融合应用与创新,具有重大的科学意义。
关于舰载机起降任务规划的研究,现有的文献主要从任务分配和路径规划2个方面展开。本文仅针对路径规划进行研究。
分析对该问题研究的文献[2-18],可以概括为2个主要方面:一方面是舰载机路径规划的建模问题;另一方面是针对模型的算法设计问题。
考虑到舰载机形状的不规则性,文献[2]将布放于甲板其他位置的舰载机作为障碍物,采用凸壳算法,将要滑行的舰载机简化为一点,而将其他障碍物舰载机进行多边形扩充,建立障碍物多边形的缓冲区,在此基础上以判断舰载机所处的路径点是否位于障碍区域来建立碰撞检测模型。文献[3]根据作业任务的需要,将舰载机描述成展翼和收翼2种状态,分别用不同的凸五边形来表示。通过计算各多边形线段间的距离来判断是否发生碰撞。在对路径规划算法的改进上,文献[2]对舰载机舰面多路径动态规划问题采用聚类粒子群算法进行求解,仿真结果表明利用聚类粒子群优化算法所求解的结果比较精确,且在出现新障碍物时,能够快速进行动态规划,其计算时间也满足实际使用的需求。文献[3]利用智能机器人行为动力学的基本原理,将舰载机路径规划的总体行为分为奔向目标行为和避障行为,并对航向角的以上2种行为策略进行改进。在动态环境中的路径规划,2种基本行为模式随着环境的变化而变化且相互制约,最终实现路径规划任务。文献[4-5]在航母甲板环境下,以舰载机自身机动能力限制和任务需求为约束条件,研究舰载机在甲板上进行移动的路径规划问题,提出了问题的概念模型,建立了包含多种约束条件的数学模型,设计了满足目标点进入方向的路径搜索算法,得到了舰载机起飞舰面滑行可行路径。最后基于每架舰载机的不同任务,分别为其规划出滑行路径。该模型能体现了舰载机高效出动和安全运行的两方面要求,并建立了与实际甲板环境相符的数学模型,为研究舰载机机队在复杂任务下的规划问题提供了依据。
上述研究都集中在单舰载机滑行时如何规避障碍物到达目标点,而没有涉及机队出动时多舰载机滑行的情况。与单机滑行相比,多机滑行的情况要复杂得多,须考虑运动舰载机之间的避障、计算效率等一系列特殊的问题。研究此问题可优化舰载机起飞滑行的路径,并得到每个时刻舰载机在甲板上的状态,可以保证舰载机在接收到出动任务后在特定区域内以优化的滑行路径到达弹射器,从而安全高效地完成任务,为舰载机群综合指挥与实时决策提供科学的理论依据和技术基础。
1 多机滑行路径规划数学模型的建立
1.1 舰载机出动任务要求
机队中的每一架舰载机需要根据命令完成各自的起飞任务。起飞任务需要考虑的约束条件包括最大路径长度Dmax、运动速度v、目标点进入方向σ。其中,Dmax限制了滑行路径长度必须小于等于一个预先设置的最大距离,v限制了舰载机滑行速度,σ限制了舰载机以特定角度范围进入目标点,以保证其顺利完成起飞任务。
1.2 舰载机简化模型
考虑舰载机之间的碰撞时,不能将舰载机用一个质点来表示。由于在路径规划中涉及舰载机的艏向及偏航角的问题,需要得到舰载机的位置信息和艏向信息,考虑到舰载机在甲板上移动时机翼均为折叠翼,将舰载机实体模型简化为与其外形相似的一个左右对称的五边形,如图1所示。
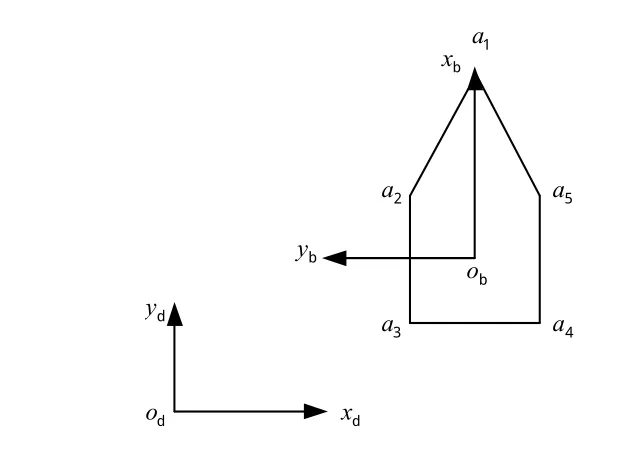
图1 舰载机简化模型Fig.1 Asimplified model of the aircraft
建立机体坐标系xbobyb,舰载机的位置信息即五边形的中心点ob的位置信息,五边形尖角部分代表舰载机的艏部,ob与a1连线的方向代表舰载机的艏向,a2与a5关于oba1对称,a3与a4关于oba1垂直对称。要确定甲板坐标系下舰载机在点ob的边界位置a1、a2、a3、a4、a5的值,只需要知道ob在甲板坐标系xbobyb下的位置(X,Y)和艏向γ(轴obyb顺时针方向转过γ即为轴obyb),根据机体坐标系到甲板坐标系的转换矩阵Lbd即可得到点(xb,yb)在甲板坐标系下的坐标(xb,yb)。
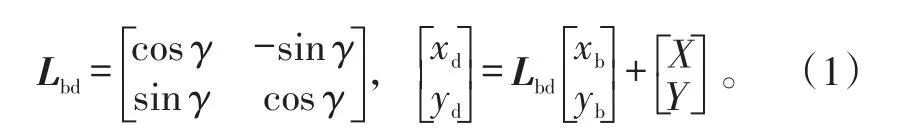
1.3 舰载机牵引系统地面运动建模
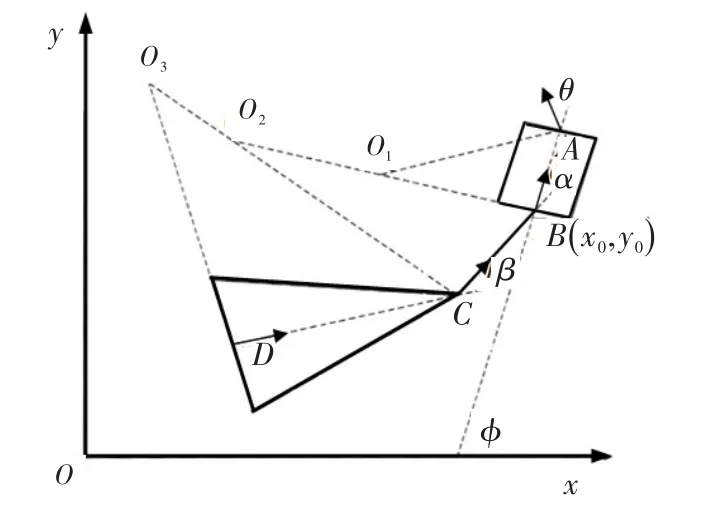
图2 舰载机牵引系统物理模型Fig.2 Physical model of carrier aircraft traction system
舰载机牵引系统是由牵引车、牵引杆以及舰载机3部分构成[13]。牵引杆与舰载机前轮转轴固连,并为了方便考虑,将牵引杆与牵引车的连接点设为牵引车后轮连线的中点。由于这里只考虑舰面上的运动,为平面运动,即单个物体有3个运动自由度,机构运动确定的充要条件是给定的独立运动参数等于机构的运动自由度数,牵引系统为五自由度系统,因而给定5个牵引系统的独立运动参数,即可获得整个牵引系统的位置姿态信息。为了得到具体的数学模型,将牵引系统进行几何简化[6],如图2所示。其在舰面坐标系上的位置坐标表示为(x0,y0),另外设牵引车轴线AB与x轴的夹角为φ,牵引车中轴线相对牵引杆的夹角为α,牵引杆相对舰载机轴线的夹角设为β,所有角度均以逆时针方向为正方向,这5个变量为牵引系统的状态变量,由这5个状态变量可以描述牵引系统任意时刻的位置姿态信息。牵引系统的运动是靠牵引车的前进和转向来完成,具体表现为速度的大小v和方向θ,这2个变量为牵引系统的控制变量。因此,舰载机牵引系统的运动学方程表示为:dzdt=f(z,u),z表示状态变量,即z=[x,y,φ,α,β]T,u表示控制变量,即u=[v,θ]T。分别在各个点对其对应的速度矢量做垂线,交点为o1、o2、o3,已知这3个点分别为牵引车、牵引杆和舰载机的瞬心,由此可得3个
图2中,矩形的4个角代表牵引车的4个车轮,A、B分别为前后车轮轴的中点,线段BC代表牵引杆,三角形代表飞机的起落架,其中,C为前起落架,D为后面2个起落架的中点。牵引车为主动运动物体,其中速度控制量由后轮提供,方向控制量由前轮提供,由于牵引车在转弯的过程中2个前轮的转向角度不一样。因此,将牵引车的方向控制量的改变定义为前轮轴中点A的速度方向,牵引车的速度即为B点的速度。设牵引车后轮轴线中点B作为牵引系统的基点,物体的角速度分别为:
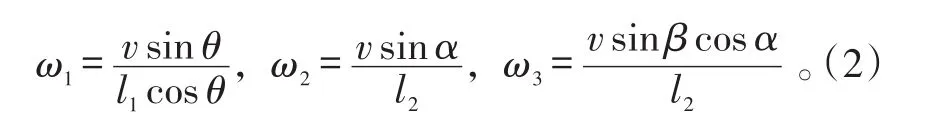
式(2)中:l1、l2、l3分别为牵引车前后轮轴的距离、牵引杆的长度以及舰载机前起落架到后起落架中点的距离。
舰载机牵引系统在前进和转弯过程中,需要考虑到整个系统的机动能力,主要表现为最大转弯角和最小转弯半径,如图3所示。
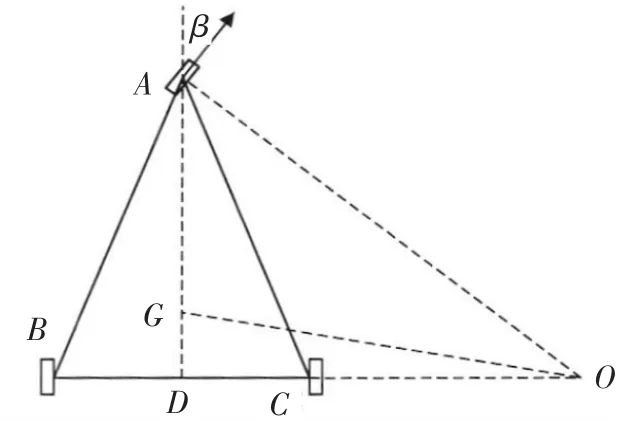
图3 舰载机转弯半径示意图Fig.3 Turning radius of carrier aircraft
以舰载机为例,三角形的3个点为舰载机的3个起落架,G点为舰载机的重心,β为舰载机前起落架偏转角,O点为舰载机的瞬心,根据其几何关系可以得到舰载机转弯半径OG关于前起落架偏转角β的表达式:即:,同时,舰载机起落架的偏转角和牵引车的偏转角有一个取值范围,表示为:βmin≤β≤βmax,θmin≤θ≤θmax,由此可得到最小转弯半径。

1.4 目标函数的建立
由弹射器工作模型和舰载机起飞间隔模型可知,每架舰载机需经过等待起动、滑行至目标点、准备起飞和等待尾涡影响消除、起飞这4个过程后才完成出动任务。设每架舰载机出动过程经历时间TA,以上4个过程经历的时间分别为T1A、T2A、T3A、T4A,TA=T1A+T2A+T3A+T4A,T3A=max(Tpre,Tvortex)表示舰载机在到达弹射器后,等待起飞的时间为准备时间和尾涡剩余影响时间中的最大值。除T4A是定值外,其余各项均与舰载机的滑行时间有关,都需优化的项目。以
由于舰载机的速度由后起落架提供,D点的速度方向为已知,因而为了简化,可将OD视为转弯半径,第一批舰载机的起动时刻为零时刻,为提高舰载机队出动率,建立优化指标:Ttotal为舰载机机队出动经历的时间,即为优化指标。
2 路径搜索算法的设计
在建立了舰载机机队出动问题的数学模型后,须要对目标函数进行优化,即对N架舰载机从停机位出发滑行到对应弹射器的路径分别进行优化。搜索算法的设计重点考虑路径节点的扩展,启发函数的选取和碰撞检测方法的进行。本文以A*搜索算法为基础,提出一种进行实时碰撞检测的方法。该方法不仅考虑了单机路径规划问题中的约束条件,而且在路径搜索每一步多次进行碰撞检测,从而有效地保证了各条路径的安全性。
2.1 节点扩展
A*算法[12]采用的代价函数为:f(x)=g(x)+h(x),其中,g(x)为从起始位置到当前节点x的真实代价,h(x)为启发式函数,表示从当前节点x到目标位置代价的估值。在A*算法进行节点扩展的每一步,总是选择使代价函数f(x)的值达到最小的备选节点作为下一个路径点。而在扩展节点时,同时将各类约束条件结合到搜索算法中能有效缩小搜索空间,提高搜索准确率,具体的方法已在以往研究文献中做了详细的介绍,本文将重点介绍满足目标点进入方向约束的节点扩展方法。舰载机准备弹射起飞时,要求机头对准弹射器跑道方向,从而保证其能够顺利完成起飞。如果当前节点x与目标点之间的距离d满足2lmin≤d≤3lmin(lmin为舰载机在开始改变前进方向前必须保持直行的最短距离)时,按照常规方法进行节点扩展来搜索除终点外的最后一个路径点,如图4所示,则很有可能由于所有备选节点均不能满足目标点进入方向的约束条件而导致搜索失败。因此,本文提出一种简捷办法来保证路径搜索的成功,使舰载机机头对准弹射器跑道方向,如图5所示。
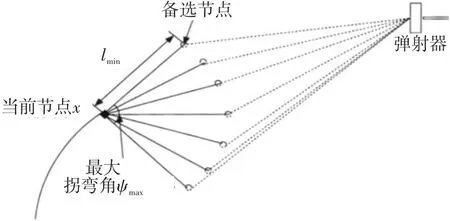
图4 按常规方法扩展节点示意图Fig.4 Extending node of conventional method
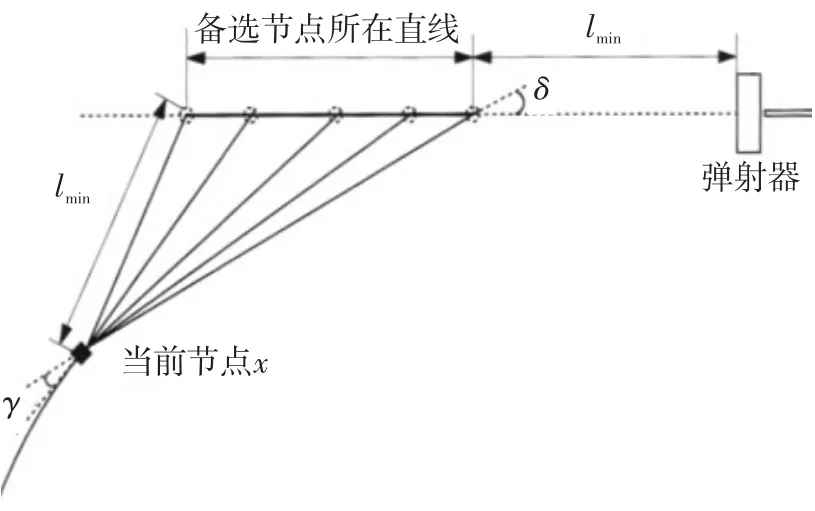
图5最后一个未知节点的扩展Fig.5 Extension of last unknown node
图5中,各备选节点均能满足最小路径段长度lmin和目标点进入方向的约束条件,只需检验其是否满足最大路径长度Dmax、避免碰撞条件、r≤ψmax和δ≤ψmax的约束条件,即可确定满足所有约束条件的备选节点,并根据各自代价函数值f(x)的大小来确定最后一个位置路径点。
2.2 启发函数的选取
启发函数h(x)的选取对于路径点的确定起到了至关重要的作用。本文根据甲板环境和任务要求,合理设计出具有动态权值的启发函数,根据舰载机距离目标点的远近来动态改变h(x)中各项的权重,使舰载机朝满足目标点进入方向的最短路径滑行。定义启发函数如下:
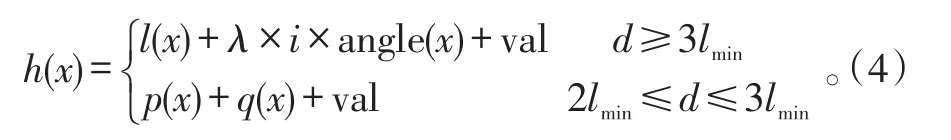
式(4)中:l(x)为各备选节点到目标点的距离;λ为权值常数;i为当前节点的序列号,即第几个路径点;angle(x)为各备选节点与目标点进入方向所在轴的夹角;val为违背量,当检测到备选节点与其他舰载机有碰撞时,则令val=∞,否则令val=0;p(x)为当前节点到各备选节点的距离;q(x)为各备选节点到目标点的距离。
以上启发函数h(x)的设计既考虑到舰载机以尽量短的距离到达对应弹射器,又兼顾了其进入目标点方向的约束条件,保证了优化路径的获得。
2.3 碰撞检测方法
碰撞检测主要通过在扩展节点时,检测备选节点所在位置舰载机是否与其他舰载机发生碰撞,即如果两个舰载机简化模型之间有重叠部分时,令启发函数h(x)中val=∞,即舍弃此备选节点,否则令val=0。具体碰撞检测过程如图6所示。
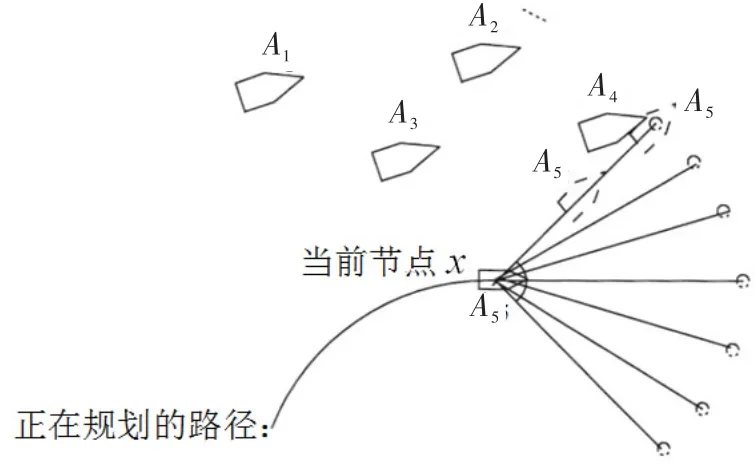
图6碰撞检测示意图Fig.6 Diagram of collision detection
图6中,A5正在进行节点扩展,A1、A2、A3、A4为甲板域中其他停放或运动的舰载机。对于A5,在各备选路径上均匀选取m个舰载机的位置,在图6中用虚线边界来表示,再用这m个位置分别与A1、A2、A3、A4进行碰撞检测,只有当备选路径段上的每一个检测位置均通过碰撞检测时,才令其启发函数h(x)中val=0,否则val=∞。以上碰撞检测方法能保证在进行节点扩展的每一步中,多次对备选路径进行碰撞检测,最大限度的避免了某些时刻因未进行碰撞检测而导致碰撞发生,提高了舰载机的运行安全。
3 算例
算例以美国“尼米兹”级航母为例,如图7所示。算例以8架(图8中的A1~A8)停靠在甲板指定站位舰载机的出动任务为例。同时,为计算便利起见,假设4号弹射器C4被占用,在此算例中不考虑。

图7 “尼米兹”级航母飞行甲板示意图Fig.7 Aircrafts on the flight deck of Nimitz class aircraft carrier
根据任务分配和时间排序仿真结论(任务分配和时间排序仿真不在本文讨论范围),可得到各弹射器上的最优起飞时序如图8所示。
由以上结果,采用本文提出的舰载机机队出行滑行路径规划算法,可以得到每架舰载机的滑行路径。图9~14为按照各舰载机的出动顺序展示的舰载机在甲板上的滑行路径。
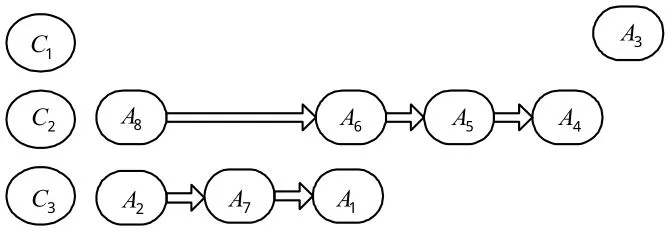
图8 各弹射器上的最优起飞时间序列Fig.8 Optimal sequence of aircrafts'launching on each catapult

图9 A2与A8滑行路径Fig.9 Taxiing path ofA2andA8

图10 A7滑行路径Fig.10 Taxiing path ofA7
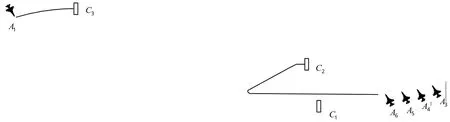
图11 A6与A1滑行路径Fig.11 Taxiing path ofA6andA1
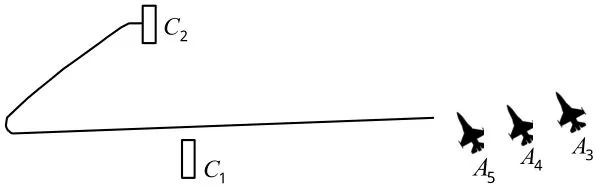
图12 A5滑行路径Fig.12 Taxiing path ofA5

图13 A4滑行路径Fig.13 Taxiing path ofA4
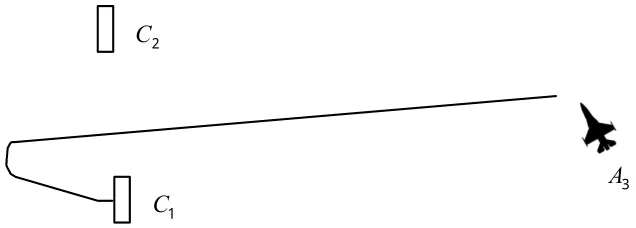
图14A3滑行路径Fig.14 Taxiing path ofA3
图9中,A8和A2是最先启动的2架舰载机,分别滑行到C2和C3起飞。而其他舰载机仍在停机位等待,待A8和A2起飞完成后才能起动。图10中,待A2起飞完成后,A7从停机位起动滑行到C3进行起飞。此时由于停放位置的限制,A3、A4、A5和A6仍需在停机位上等待,才能保证出动安全时从停机位起动。图11中,A6和A1分别从停机位起动,滑行到C2和C3进行起飞,A3、A4和A5仍需在停机位等待。图12和13中,A5和A4依次滑行到C2进行起飞,甲板上只剩下A3仍未启动。图14中,由于除A3外C1前没有其他舰载机,故C1此时是可用的。A3将滑行到C1起飞。
依据上述结果,给定已知的舰载机在甲板上的滑行速度、在弹射器上准备起飞的时间、起飞过程需消耗的时间,就能得到每个时刻各舰载机在甲板上的位置和移动方向。
4 结论
与单机滑行相比,飞行甲板多机滑行须要考虑运动舰载机之间的避障、计算效率等问题。本文建立了多机滑行路径规划数学模型,包括舰载机简化模型、舰载机牵引系统运动模型、舰载机碰撞检测模型,以及目标函数等。在设计基于A*的路径优化搜索算法,提出了一种简捷办法来保证路径搜索的成功,使舰载机机头对准弹射器跑道方向;启发函数既考虑舰载机以尽量短的距离到达对应弹射器,又兼顾其进入目标点方向的约束条件;碰撞检测不仅考虑单机路径规划中的约束条件,而且在节点扩展的每一步多次对备选路径进行碰撞检测。
针对舰载机队出动路径规划问题,本文提出的方法可优化舰载机队起飞滑行的路径,可以保证舰载机在接收到出动任务后在特定区域内以优化的滑行路径到达弹射器,给定已知的舰载机在甲板上的滑行速度、在弹射器上准备起飞的时间、起飞过程需消耗的时间,可得到每个时刻每架舰载机在甲板上的状态,为舰载机队综合指挥与实时决策提供科学依据,确保舰载机队安全高效地完成出动任务。
实际上,舰载机起降任务规划不仅需要考虑舰载机队在甲板的出动时序及路径规划问题,还需要考虑弹、油、气、液等舰面保障作业规划,这些保障作业与起降作业高度耦合,组成一个更复杂、庞大的作业系统。在本文研究的基础上,下一步需要开展考虑舰面保障作业的舰载机机队起降任务规划研究。
