舰载机无杆式牵引车纵向动力学分析

戚基艳,金嘉琦,邹姗姗

(沈阳工业大学 机械工程学院， 沈阳 110870)

舰载机调运是航母舰基保障的重要环节[1]，无杆式牵引车作为舰基保障的一种新型设备，在现代舰载机调运中被广泛使用[2]。无杆式牵引车能够更好地融合先进的设计技术，操纵稳定性、灵活性更高，是未来舰载机牵引车发展的趋势[3-6]。主要应用于中小型飞机的电力驱动牵引车[7]，很好地解决了噪声和环境污染问题，因为通过性好的优势，被舰载机调运广泛采用。目前国内外对无杆式牵引车的相关研究主要集中在整体结构参数和夹持——举升机构的设计仿真以及牵引运动的稳定性、平顺性、制动性等行驶可靠性方面为主[8-12]。对于舰载机无杆式牵引车系统纵向受力分析方面，没有基于复杂的海洋应用环境，建立通用的数学模型，没有考虑铰接点的耦合作用[13-15]；对于舰船上的牵引车研究主要以起飞和着舰动力学特性为主[16-17]，对于舰船上的牵引运动主要研究行驶的横向稳定性[10]。

本文通过建立舰载机无杆式牵引车坐标系，针对海洋环境的特殊性，考虑坐标转换的准确性，按照航向、纵摇、横摇建立船体三自由度耦合的牵引车纵向行驶动力学模型，并通过Matlab/Simulink建立考虑海洋环境的仿真模型。考虑实际运行的需要，通过设置不同的仿真运行条件，利用ADVISOR软件验证了模型的正确性。进一步分析了舰载机无杆式牵引系统纵向稳定匀速行驶的前提条件，为后续舰载机无杆式牵引车纵向稳定行驶的深入研究提供了方法和方向。

1 牵引车参数

本团队在前期已经完成了对轮毂电机驱动的舰载机无杆式牵引车的结构设计(如图1)，并进行了静力学与模态分析的研究[18]，为了便于描述，下文中提到的牵引车均指舰载机无杆式牵引车。采用轮毂电机作为驱动力，无驾驶室，不需要机械作为中间传递机构，简化了驱动系统，减少了动力损失和使用故障率，提高了整车的传动效率，减少对空间占用率，很好地解决了传统无杆式牵引车存在的诸多问题[7]。引入无人驾驶技术，采用无线遥控功能，减少操作人员的误操作和工作负担，改善了操作环境，提高了工作人员的利用率[8]。为了提高系统牵引运动转弯时的操控准确性，在对牵引车结构设计时，已将舰载机作用于牵引车部分的重量与两后驱动轮轴线中心点重合。自主设计的牵引车的性能参数如表1。

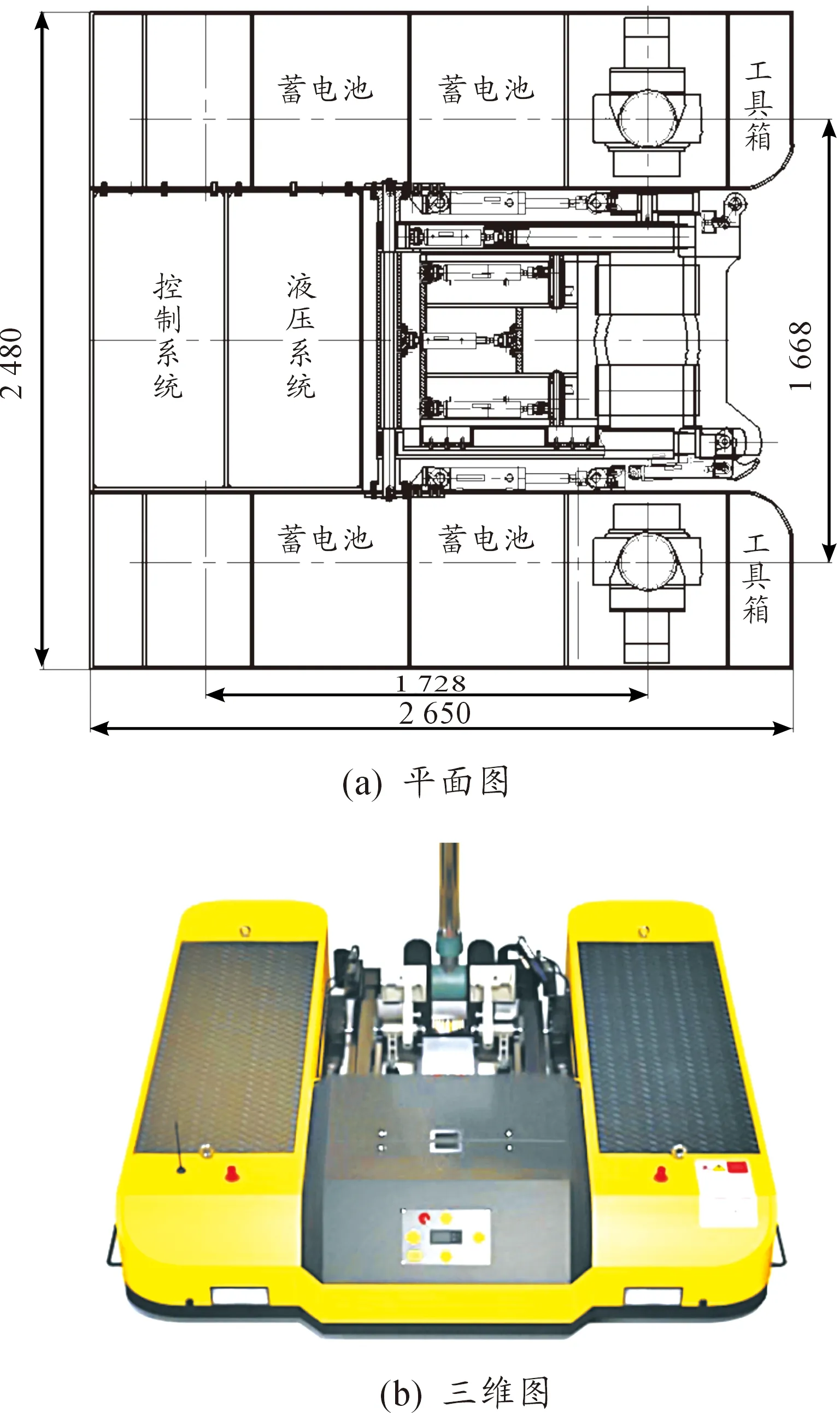
图1 自主设计的舰载机无杆式牵引车结构示意图

表1 牵引车的性能参数

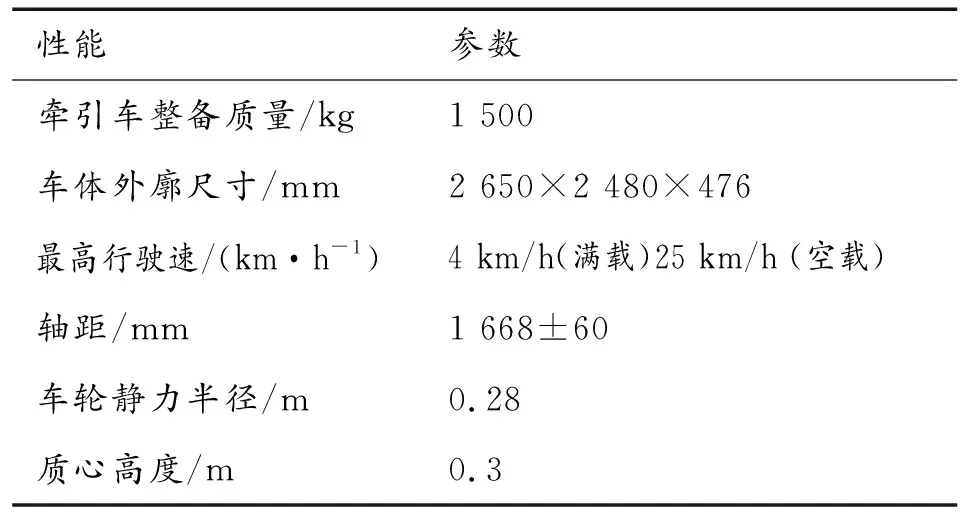
性能参数牵引车整备质量/kg1 500车体外廓尺寸/mm2 650×2 480×476最高行驶速/(km·h-1)4 km/h(满载)25 km/h (空载)轴距/mm1 668±60车轮静力半径/m0.28质心高度/m0.3

2 舰载机-牵引车系统坐标

由于舰载机牵引车的运动受海洋多自由度的耦合运动影响较大，因此必须建立牵引车坐标系和惯性坐标系之间的关系[7]。建立的系统动力学模型如图2所示，其中，牵引车坐标系参照国际汽车工程师协会制定的车辆标准坐标系，舰船运动坐标系采用由造船和轮机工程学会推荐的常用体系[19]。

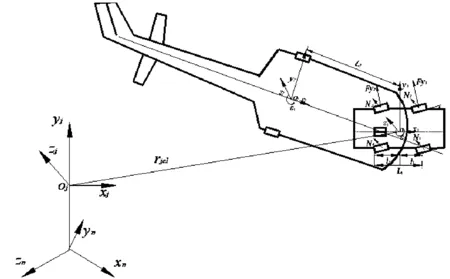
图2 舰载机无杆式牵引车牵引系统模型示意图

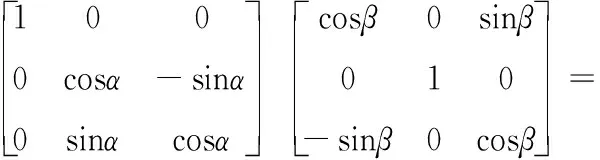
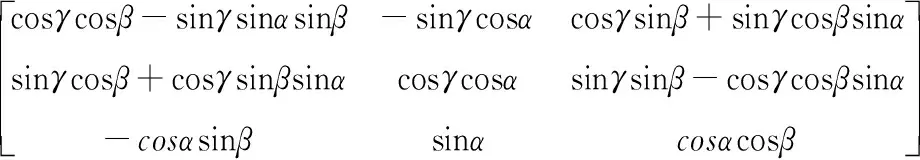
(1)

由于舰船甲板面比较平坦且轮毂电机驱动的牵引车没有像汽车悬架带来的平顺性影响，牵引系统行驶时其相对甲板的俯仰，侧倾以及垂向自由度影响较小，因此可以不考虑[22]。则船体坐标系到牵引车——舰载机连体坐标系的转换关系可以表示如下[23]:

(2)

式中：θi(i=1,2)为牵引车和舰载机的连体坐标系相对于船体坐标系的横摆角。

3 牵引车纵向动力学模型建立

牵引车和舰载机在自身坐标系下所受的纵向外力主要包括：滚动阻力、空气阻力、轮胎侧偏力、铰接点处作用力，重力在连体坐标系的分力[10]，借鉴汽车系统动力学，车轮的滚动阻力包括了轮胎侧偏力[20]。因此，根据汽车动力学方程[24]和建立的系统坐标系，可得出牵引车—舰载机系统的纵向动力需求平衡方程为：

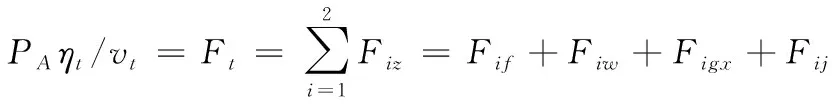
i=1,2

(3)

式中：Ft为牵引车所需的驱动力；Fiz代表牵引车和舰载机行驶过程中受到的阻力；Fif为牵引车和舰载机的滚动阻力；Figx表示重力在连体坐标系的纵向分力，根据海况的不同，该力作为阻碍和加速系统运动的力[10]，作用在牵引车和舰载机上，作用类似于汽车行驶方程式中的坡度阻力；Fiw为牵引车和舰载机的空气阻力，Fiq为舰载机和牵引车铰接点处的纵向外力；Fij为牵引车和舰载机的加速阻力。

3.1 滚动阻力分析

以牵引车为例，连体坐标系下所受的滚动阻力为[9,23]：

(4)

式中：F1f为牵引车在甲板上行驶的滚动阻力；f1为牵引车在甲板上的滚动阻力系数；Ni为牵引车自身不提供驱动力和制动力的前提下，牵引车各轮胎所受的支持力，根据对牵引车进行受力分析，可得：

(5)

式中：N1，N2，N3，N4为牵引车左、右前轮和左、右后轮的垂向受力；L1为牵引车轴距；l1、l2为牵引车前轴和后轴到质心的距离；l6为牵引车左右轮的轮距；h1、h2为牵引车质心和舰载机—牵引车系统的铰接点距地面的高度；qx、qy、qz为牵引车的重力在自身坐标系各坐标轴下的投影；F1qx为牵引车在铰接处点的所受的纵向力。

将(5)代入式(4)整理得:

F1f=f1(-qz)

(6)

牵引车所受重力在自身坐标系和惯性坐标系下的转换关系为：

(7)

因此，牵引车在惯性坐标系下的滚动阻力为：

F1f=cosαcosβp1f1

(8)

p1为牵引车在惯性坐标系下的重力。对于舰载机来说，前鼻轮被抬起，按照受力分析推导，模型需要的已知数据较多[10]，计算复杂，为了简化模型，对舰载机所受的支持力做如下假设：由于主要研究的是舰载机的垂向受力对纵向滚动阻力的影响，可认为舰载机是左右对称结构，借鉴汽车模型构建方法，在满足一定假设条件下，将舰载机和牵引车简化为“单轮车辆”模型[24]，则可认为二者所受的滚动阻力分析方法是一样的，可以根据式(8)计算飞机所受的滚动阻力。

3.2 加速阻力分析和空气阻力分析

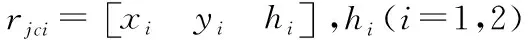
(9)

式中：δi(i=1,2))为牵引车和飞机的旋转质量转换系数[25]。

甲板上紊乱的气流对牵引车和舰载机会产生复杂的多方向作用力[26]，根据对牵引车在舰面上经常行驶的区域进行分析，忽略凸起建筑物对纵向气流的影响，牵引车在甲板上的纵向空气阻力可以表示为[10]：

(10)

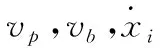
3.3 舰载机所需牵引力分析

将牵引车和舰载机作为分离体来考虑时，舰载机被牵引匀速行驶时，结合式(3)、式(8)、式(10)，可知此时舰载机的纵向受力为：

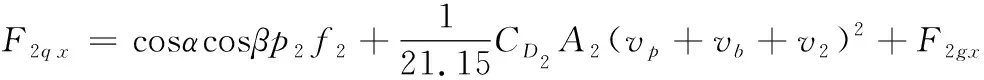
(11)

根据图2分析可知，铰接点处牵引车和舰载机的受力，有如下非线性关系[28]：

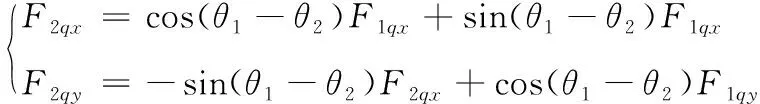
(12)

当Δθ=θ1-θ2的值很小时，根据式(12)可认为：

F2qx≈F1qx

(13)

根据式(7)可知，牵引车和舰载机的重力在连体坐标系的x轴方向的分力为：

Figx=(cosθi(cosγsinβ+sinγcosβsinα)+

sinθi(sinγsinβ-cosγcosβsinα))(-pi)

(14)

结合式(3)、式(14)，可以得出牵引车和舰载机分别所受的纵向外力动力学模型如式(15)所示，也可以进一步算出牵引车动力需求的功率[25]。

(15)

4 仿真模型搭建

设定牵引车和舰载机的纵向速度相等，牵引车和舰载机的相对横摆角的差Δθ很小可以忽略不计，牵引车参数如表1，舰载机的相关取值参考文献[29]，在Matlab/simulink中建立牵引车——舰载机系统纵向受力仿真模型并进行封装如图3所示。

图3 封装后纵向受力仿真模型示意图

其中框图1，2，3是输入参数系统，分别是牵引车参数，海况参数和舰载机参数，可以根据实际需要修改。由于海况复杂，考虑本文研究海况对牵引车纵向动力需求的总体影响和力的大小进行分析，假设航向不变的前提下，对代表海况的横摇，纵摇的角度进行适当简化。考虑到风速与海况一一对应[30]，采用波形输入，将横摇、纵摇角度和风速设为周期相同(4 s)，保证对应关系不会被破坏，仿真时长为20 s，按照中等海况下的舰船运动数据作为最大值[31]，递减设置数值，海况三维模拟数据输入如图4。

图4 模拟不同海况的三维数据图

对于纵向受力封装子系统模型组成部分与式(15)中各项对应，F1f、F1w、F1j、F1qx、F1gx、F2gx仿真模型依次如图5～图10。

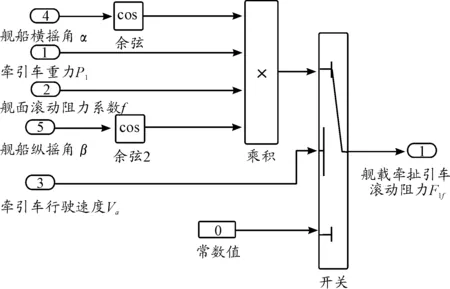
图5 滚动阻力仿真模型(F1f)示意图

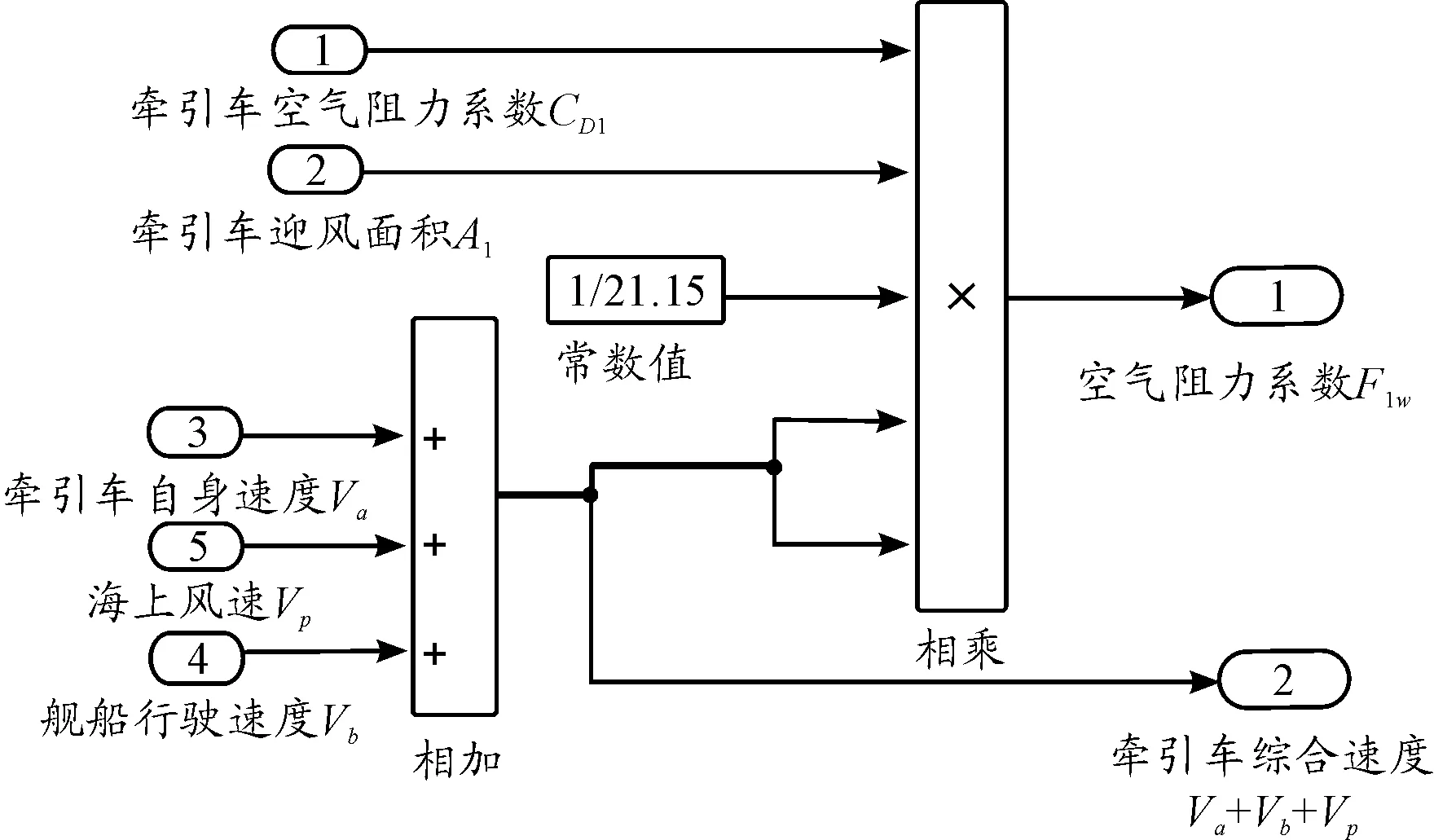
图6 空气阻力仿真模型 (F1w)示意图

图7 加速阻力仿真模型 (F1j)示意图

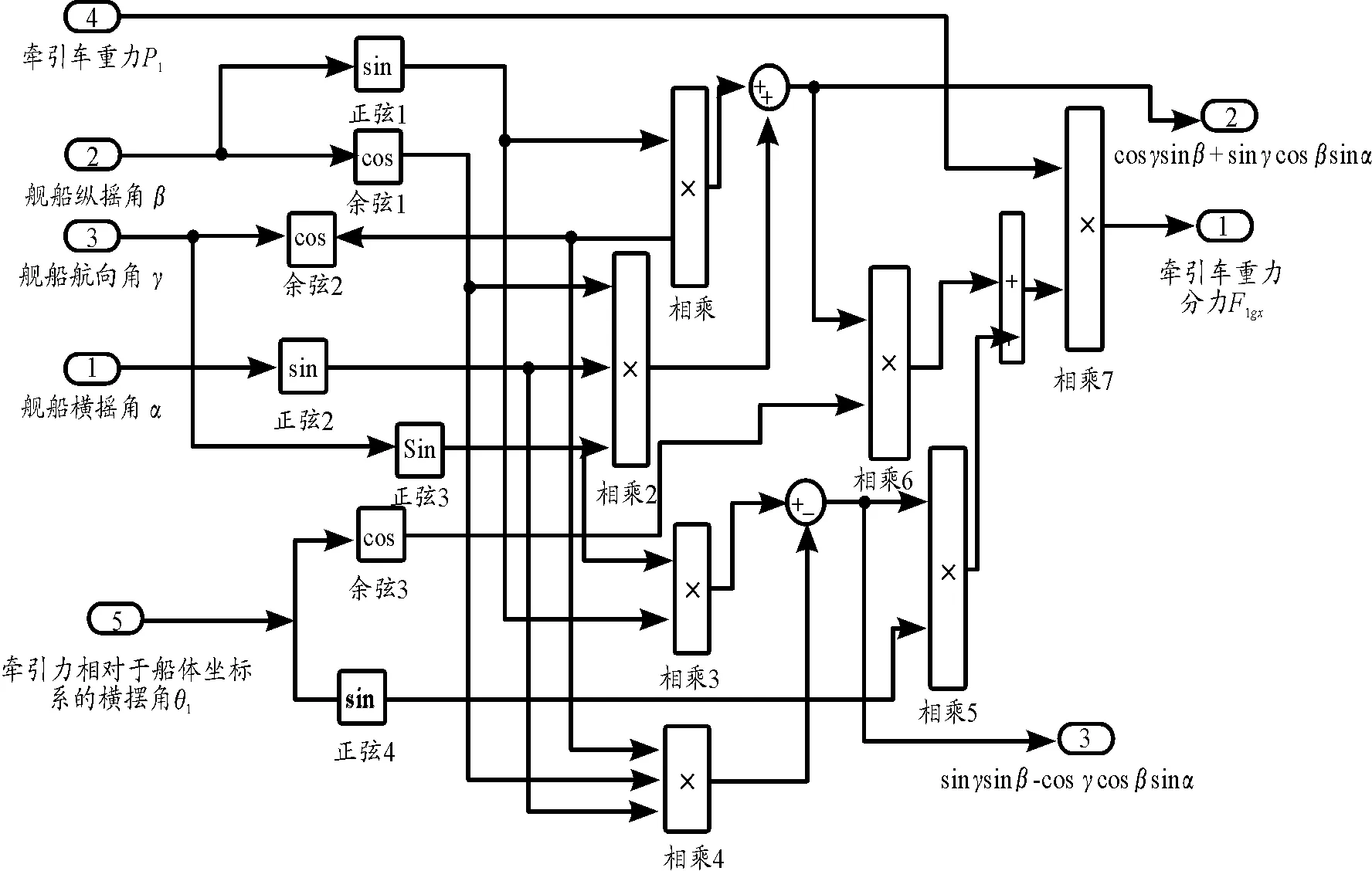
图8 牵引车所受重力在连体坐标系的x轴方向分力(F1gx)

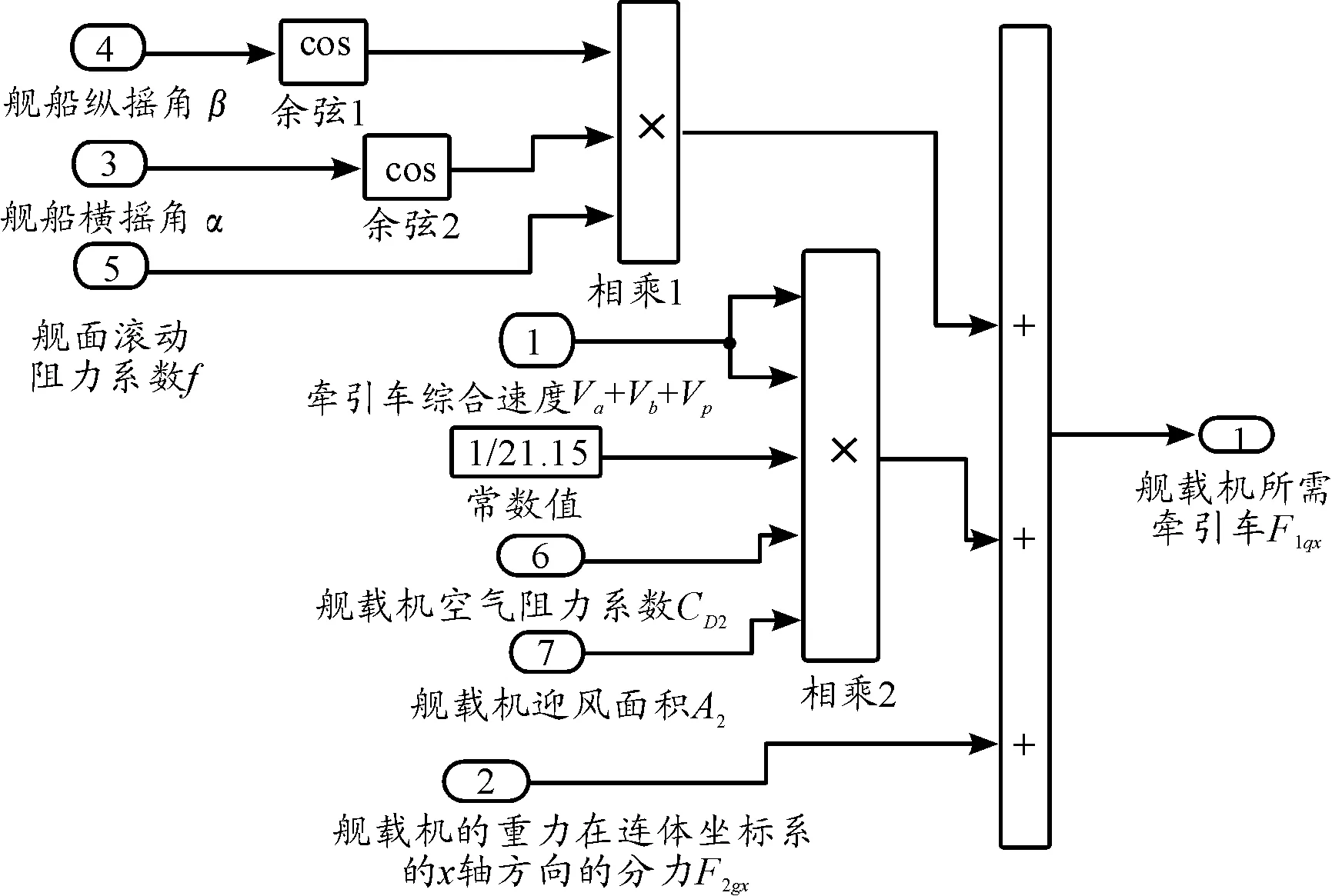
图9 舰载机所需牵引力 (F1qx)示意图

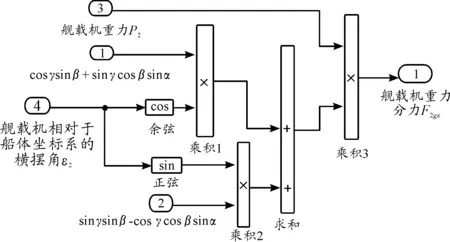
图10 舰载机所受重力在连体坐标系的x轴方向的分力(F2gx)示意图

通过仿真实验结果(图11)分析得到目标牵引车在中等海况下匀速行驶所受的最大阻力为31.36 kN，根据式(3)传递效率取0.95时，所需的功率为45.59 kW。

所设计的牵引车的全部动力均来自于装在牵引车轮毂内的电机，牵引车的纵向牵引力必须满足动力最大需求状态，即具有克服最大阻力的能力。因此，为了验证模型的正确性，将舰载机所需的牵引力等效为牵引车的载重，将相关参数导入到验证汽车动力性的软件ADVISOR中，参考轮毂电机驱动的汽车相关设置方法[32-33]将模型参数进行修改设置。牵引工作时，即满载时，在CYC_CONSTANT循环工况下，进行仿真，将运行速度设置为4 km/h (2.49mph)，时间与车速的关系矩阵修改为cyc_mph=[0 0;5 vel;45 vel;50 0;55 vel;95 vel;100 0;105 vel ;145 vel;150 0;155 vel;195 vel;200 0;205 vel;245 vel;255 vel;295 vel;300 vel ]。空载时，为了能够更好的体现牵引车的机动性和扩展使用功能[34]，选择CYC_BUSRTE循环工况，最高速度为29 km/h(18 mph)，一次循环内28次启停，满足空载设计最高速度和运行环境的要求。仿真结果如图12所示，通过对比循环工况需求车速与仿真实际运行速度结果可知，根据分析所得的纵向力计算的电机功率满足运行要求，所建立的牵引车纵向力仿真模型准确可靠。

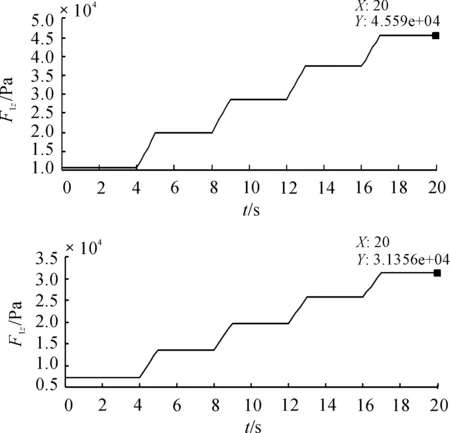
图11 纵向阻力与牵引车功率仿真结果

5 舰载机牵引车系统的纵向行驶稳定性讨论

舰船坐标系下，无杆式牵引车和舰载机位置(车速)之间的关系如图13，定义(xi，yi，θi) (i=1，2)为舰船坐标系中牵引车和舰载机的位形，牵引车牵引舰载机向前运行时，牵引车的系统运动学方程可以描述如式(16)：

(16)

其中：v1为牵引车在舰船坐标系下的移动速度，p(xi,yi)为牵引车驱动轮和舰载机主起落架轮轴中心点在舰船坐标系下的坐标；θi(i=1，2)为牵引车和舰载机的坐标系与舰船坐标系的夹角，φ表示牵引车前轮与牵引车坐标系横轴y的夹角，L1为牵引车前后轮轴之间的轴距，L2为舰载机主起落架轮轴到铰接点距离。

图12 实际车速与循环工况所需车速仿真结果

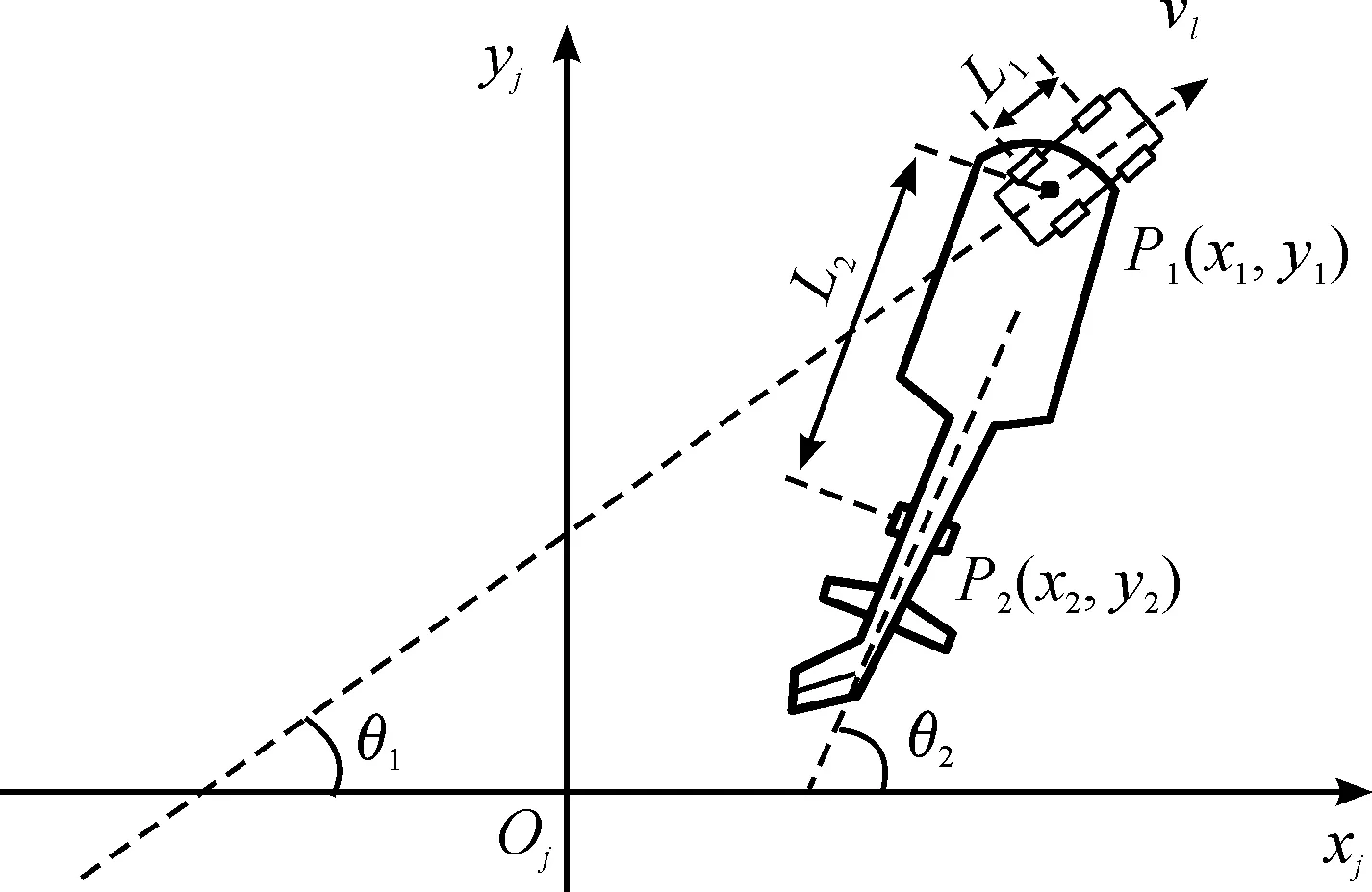
图13 舰船坐标系下的牵引系统模型示意图

根据图13分析，可知牵引车和舰载机之间几何关系为:

(17)

则舰载机在舰船坐标系下的行驶速度为：

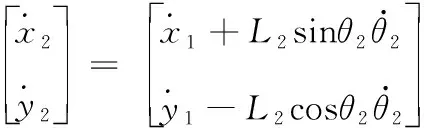
(18)

根据式(18)可知，保证牵引车和舰载机在舰船坐标系下等速行驶的前提条件是θ1=θ2或θ2=0。

进一步讨论，牵引车—舰载机系统纵向等速运行的稳定条件。牵引车和舰载机铰接点没有侧向移动情况下，铰接角Δθ产生摆动时的微分方程为：

(19)

其中:m2是舰载机质量；IZ2是舰载机的转动惯量；Cf是舰载机轮胎的侧偏刚度，这种运动是一种典型的有阻尼的衰减振动，参考文献[35]，该方程的稳定解为Δθ=0。

通过以上分析可得出：牵引车牵引舰载机纵向等速稳定运行条件为：θ1=θ2，如果不能保证这种状态，需要采用一定的控制器[29]，通过直接或间接控制铰接角的横摆位移来保证系统的稳定运行。

6 结论

结合汽车动力学验证软件ADVISOR，根据舰载无杆式牵引车实际运行环境，设置不同条件，仿真实验结果证明了所搭建模型的正确性。该模型可以通过输入不同的参数，分析不同参数的舰载机无杆式牵引车纵向受力情况。

通过分析目标牵引车位形方程和铰接角横摆运动学方程，给出舰载机无杆式牵引车纵向匀速稳定运行的条件是牵引车和舰载机与舰船横摆角相同(θ1=θ2)，否则需要控制器介入。