数学中也有实验和创造——以一节圆锥曲线的探究课为例

江苏省扬州中学 (225009)

姜卫东

1.引言

在一次校际交流活动中，笔者要到对方学校开设一节圆锥曲线的复习课.众所周知，传统的数学复习课，无非是这样的几个环节：知识点复习→例题精讲→课堂检测→课外作业.笔者决定打破这个俗套，来一次复习课的创新设计，让学生感受到数学中不仅有概念、公式、定理、证明与计算，更有大量的实验与创造！基于这样的思路，笔者设计了一节有关圆锥曲线复习的探究课.

2.课堂实录

2.1 创设情境 引入课题

图1

师：同学们都知道鲁班从野草的叶子联想到锯子.今天，我们就从圆想开去，看看能得到什么成果？首先，请同学们回忆一下，圆中有哪些性质？

生：直径所对的圆周角为直角.

师：如图1，在直角坐标系中，若AB为圆O的直径，则有∠APB=90°,∴kPA.kPB=-1(1).圆中还有哪些性质？

生：垂径定理.

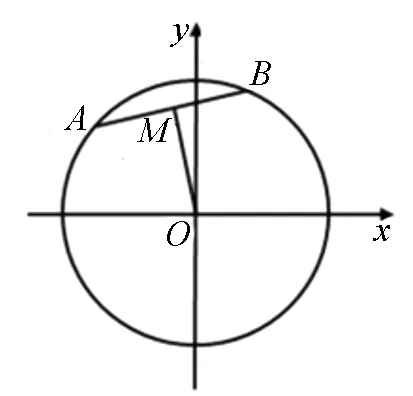
图2

师：对！如图2，在圆O中，若点M为弦AB的中点，则OM⊥AB,∴kOM·kAB=-1(2).

椭圆可以看成是将圆拉伸或压缩而得到，以上圆中的性质(1)与(2)在椭圆及双曲线中是否也成立呢？接下来，我们一起来开启探究之旅！

设计意图：圆是学生熟悉的几何图形，初中已研究过它的几何性质.在高中解析几何中，又通过解析法得到了圆的方程，并在此基础上研究了直线与圆、圆与圆的位置关系，学生对圆的相关知识已经非常了解，而且在伸压变换下，圆与椭圆可以进行互化，所以这两种曲线之间存在着一种必然的联系.因此，设计时从回忆圆的性质出发，让学生进行类比联想，猜测椭圆等圆锥曲线的类似性质.

2.2 问题引导 探究新知

图3

(学生经过短暂的思考，很快给出了答案)

生：从图形上直观判断，就发现PA与PB不垂直，这时kPA·kPB≠-1.

图4

生：应该是吧？

师：听大家的语气，好像还不太肯定.那么，下面我们就试着进行证明，请同学们自主探究.(学生经过一段时间的思索，有部分学生得出了结论，老师将一个学生的过程进行投影展示，并适当点评)

图5

(一石激起千层浪，学生一下子活跃起来，有的说是，有的说不是)

师：口说无凭，数学中讲究严谨性，要么进行严格论证，要么举反例进行否定.下面请同学们分小组进行合作学习与探究，然后请小组代表发言.

生：我们小组经过证明，发现结论仍然成立，理由如下：

师：前面，我们通过探究，发现创造了椭圆中的两个结论，它们之间又有什么联系？

生：在两种情况下，A、B这两个点都是关于原点O对称的！

师：对！实际上，说得更透彻一点，第一种情形可以看成是第二种情形的特例，而第二种情形才更具一般性.以上结论在椭圆中是成立的，我们再做一次思想实验，类比一下，这个结论在双曲线中是否也成立呢？请同学们自己写出问题及结论.

(提出问题比解决问题更重要！)

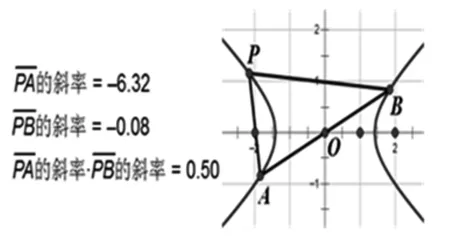
图6

师：这位同学提出的问题是否正确？我们来进行实验.如图6，在几何画板中，拖动点P，请同学们观察kPA·kPB值的变化情况.

师：根据前面的探究学习，椭圆与双曲线中kPA·kPB都是定值，但表现形式不同，能否将它们的形式统一起来？

(学生一下子找不到思路，老师适时进行点拨，引导学生圆锥曲线中有一个共同的重要的量，即离心率，从而启发学生将kPA·kPB向e转化)

(通过以上的讲解，学生惊讶地发现，这个定值居然是统一的.感叹之余，也让学生体悟到数学的统一美与简洁美！)

师：关键是看它的轨迹方程是什么？通过方程判断点P的轨迹是否为椭圆？如何求点P的轨迹方程？

师：下面我们再由圆中的垂径定理进行联想、类比和实验.先看椭圆中的情况.同学们，你会提出怎样的问题呢？

(学生直觉判断kOM·kAB应该是一个定值，但不知具体值为多少)

图7

师：还有其它的解法吗？

生：也可以假设直线AB的斜率为k,设出直线AB的方程，利用直线与椭圆的位置关系及中点坐标公式，求出中点M的坐标，进而表示出直线OM的斜率.

生：也可以直接设点A,B的坐标，求出中点M的坐标，表示出kAB·kOM，并利用A,B两点在椭圆上对所得式子进行化简.

师：同学们，能否利用前面已经得到的结论来解决这个问题呢？

图8

师：太好了！根据这位同学的回答，我们发现上面讨论的两个问题，在本质上是完全一致的！

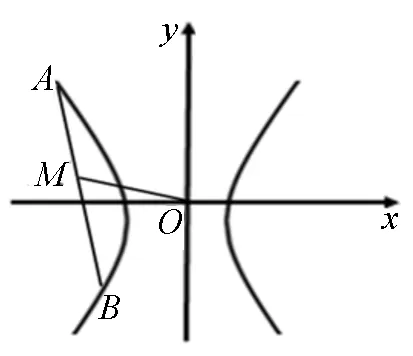
图9

师：在椭圆与双曲线中的结论表面上形式不同，能否将它们统一起来？

(由于类似的问题在前面已探究过，所以学生不难找到答案)

生：这两个结论可以统一写成kAB·kOM=e2-1.

设计意图：通过伸压变换，将圆变化为椭圆后，此时圆中的两个重要的性质，即“直径所对的圆周角为直角”和“垂径定理”，在椭圆中已经不再成立！那么，又会是什么性质呢？为此，教师组织学生进行实验，先通过几何画板等软件进行动态演示，然后再进行思想实验，即大胆猜测，最后给出严格的证明.让学生经历一次“再发现，再创造”的过程，这是第一次实验与创造.在得到椭圆中的相关结论后，又进行第二次实验与创造！即大胆地将椭圆中的结论类推到双曲线中，通过实验与尝试证明，最终发现这些结论在双曲线中也是正确的.不仅如此，在椭圆与双曲线中的结论可以完成统一起来，可用同一个表达式来表示！接下来，又进行第三次实验与创造，那就是探究上面得到的统一结论的逆命题是否成立；通过求解动点的轨迹方程，利用方程研究曲线的性质，得到它的逆命题也是成立的！实质上，这就是椭圆与双曲线的第三定义.课上到这里，师生并未停下探究的步伐，又进行了第四次实验与创造，通过对证明过程的辨析，发现椭圆与双曲线中得到的这两个性质在本质上又是完全一致的！

3.教后反思

(1)在学生头脑中根植一种观念.在学生的头脑中，一直存在着一种偏见和误解，那就是只有物理、化学等自然科学中才存在实验和创造，在数学学科和数学课堂中，无非就是各种定义、法则、公式或定理等等，好像与实验、创造无关.事实当然并非如此，数学中结论的得来不是空穴来风、从天而降，它是通过实验、创造而来.这里的实验不仅包含操作类实验，也包含人的思想实验，这两种实验相互结合，产生数学中的发现和创造.

(2)教会学生一种探究数学的方法.新课程理念要求从传统的接受式教学向探究式教学转变.如何进行探究式教学?方法众多，本节课向学生提供了一种探究数学的模板，即实验→猜测→验证→创造.其中数学实验使学生提出问题、“发现数学”、“创造数学”成为可能.学生可以通过专门的数学软件进行具体的操作演示，发现其中蕴含的数学规律，再通过理性思维进行数学的抽象概括，形成数学的判断及结论.当然，这些判断及结论也不一定正确，还需要进行确认证明.这就是一条探究数学的有效路径，也是让学生从“懂数学”到真正“会数学”的根本转变，更是让学生学会“数学地思维”的必由之路.

(3)培育学生核心素养的有效路径.在本节课中，先通过对圆中的有关性质类比联想，借助合情推理，猜测椭圆中的相关结论，然后进行数学实验，直观感知数学结论的可行性，最后通过逻辑推理确定它的真实性.在这个过程中，学生的直观想象与逻辑推理得到有效的提升.同时，在整个探究教学的过程中，从图形中观察的几何性质上升为数学结论，以及从椭圆推广到双曲线等，无一不需要学生进行数学抽象与数学建构，它们的综合作用也正是培养学生理性精神、培育学生数学核心素养的有效路径.

(4)几点改进.这节数学探究课是笔者进行的一次尝试，目的在于使学生认识到数学中也有实验和创造.但在具体实施教学的过程中，尽管学生对这种教学形式感到新颖，但笔者也发现学生对这种探究教学的模式还不太适应，对于如何进行数学实验？如何进行数学创造？学生有时会感到无所适从，不知从哪里入手？实验与创造的过程中有哪些环节？要注意哪些问题等？因此，要真正让学生适应这种教学模式，真正掌握并学会使用“实验→猜测→证明→创造”这种思维模式，还需在今后的教学中进一步强化！