一道高考染色问题的创新解法及推广
2019-04-28江西省宜丰中学336300
江西省宜丰中学 (336300)
晏伟峰 曹宇淇
在高考题及全国数学联赛中常遇到不同的染色问题,许多染色问题的模型得以建立并得到了具体的求解公式.而在平时的教学过程中,像2010年天津理科卷第10题这种类型的染色问题,学生由于不能正确地选好分类标准和优化分类顺序,尽管教学多遍效果甚微.在竞赛中也碰到过类似的问题,为了更好将此类染色问题模型化,构造转化为熟悉的数学问题,我们进行了方法的创新及推广,欢迎大家指正.
例(2010·天津10)如图1,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法共( ).
A.288种B.264种
C.240种D.168种
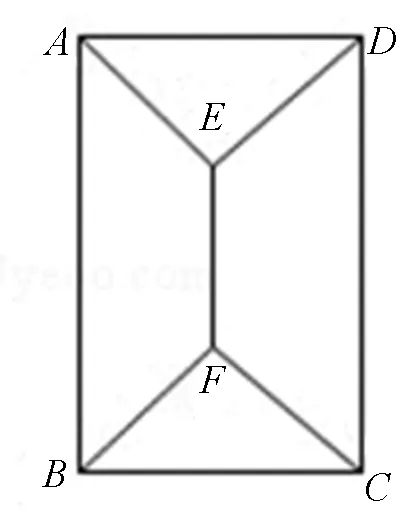
图1
分析:由题意知图中每条线段的两个端点涂不同颜色,可以根据所涂颜色的种类来分类:
当B,D,E,F用四种颜色,B,D,E,F用三种颜色,B,D,E,F用两种颜色,分别写出涂色的方法,根据分类计数原理得到结果.有老师给出过这题的五种证法,但均不能模型化这类染色问题,下面仅给出高考标答中的解析.
解:∵图中每条线段的两个端点涂不同颜色,可以根据所涂颜色的种类来分类:



根据分类计数原理知共有24+192+48=264种不同的涂色方法.
点评:本题主要考查排列组合的基础知识与分类讨论思想,属于难题.天津卷中的排列、组合问题有几年处于压轴题的位置,且均考查了分类讨论思想及排列、组合的基本方法,要加强分类讨论思想的训练.
创新方法二:在文献[1]中我们知道伯努利信封装错问题中n封信全装错的解法为
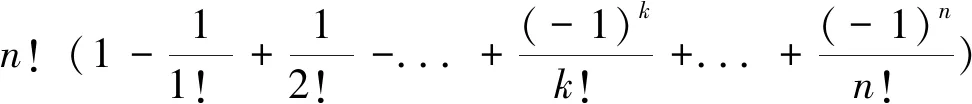
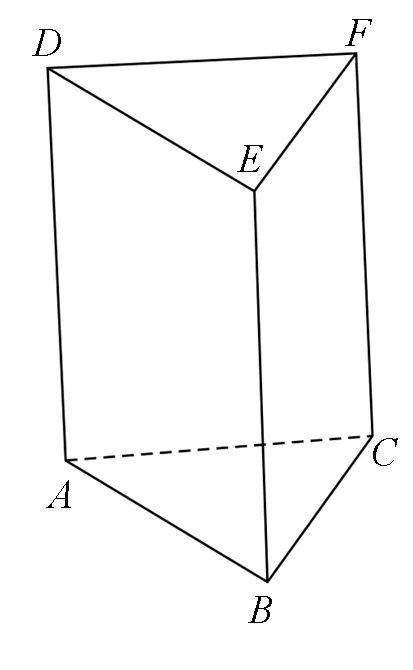
图2

图3
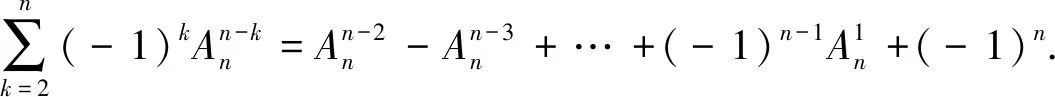
变题用五种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法共 种.
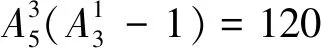
方法三:上述问题1中公式还不太完美,能不能有一种公式适合n≥3种颜色的情况?我们知道信封装错问题的计算公式证明可以用容斥原理,因此我们直接用容斥原理可以推得更好的公式如下:

本文从高中数学中的分类讨论思想和构造转化思想入手,借助容斥原理及信封装错模型,很好的将高考数学中的热点题材中的一类特殊染色问题模型化.
