基于供应链回购契约的两阶段订货策略研究

董兴林，齐 欣 DONG Xinglin,QI Xin

（山东科技大学 经济管理学院，山东 青岛 266590）

0 引 言

随着技术进步和消费者偏好的变化，一些产品价格会随时间的推移而不断下降[1]。由于市场需求具有动态不确定性，因此，零售商要制定恰当的订货策略以最大化自身利益引起人们的广泛关注。官振中、李晓力[2]在供应商供货有次品的背景下，建立了易逝品需求是随机的且受价格影响的最优订货策略，以期获得最大利润。徐贤浩、陈雯等[3]基于需求预测理论，以短生命周期产品为研究对象建立了三种订货策略模型。徐永锋[4]从信用支付角度研究易逝品订货策略，通过对零售商与批发商的利润分析，建立供应链总利润函数，并对不同参数取值下的最优订货策略进行分类讨论。

供应链回购契约是运营管理领域较为广泛应用的一种协调机制，它允许零售商在销售期结束时将没有卖出的产品以一个低于批发价的价格退还给供应商，从而使市场需求不确定性而引起的风险由供应商和零售商共同承担，平衡两者的边际收益以实现供应链协调。国内外学者对于回购契约影响供应链决策的研究较多。Taylor[5]指出回购契约可以刺激零售商提高销售努力，但没有考虑对零售商利润的影响。李娟[6]等讨论了二次销售及回购契约下策略型消费者的行为对供应链整体库存的影响。张新鑫[7]等、代建生[8]等考虑带风险偏好的回购契约对供应链系统的影响，并分析了不同回购契约及不同促销效应下供应链成员的协作关系。胡觉亮等[9]讨论了二级服装供应链的回购契约收益模型，研究了回购契约的不同参数对供应链利润的影响，并进一步讨论了多阶段定价的订货问题模型。

通过研究发现，大部分学者只讨论回购契约或者从需求理论、价格理论出发研究产品的订货策略。事实上，由于策略型消费者的存在，零售商会进行分阶段销售，供应商则会对销售期末的产品进行回收。鉴于此，本文针对一个供应商、一个零售商和顾客群所组成的供应链系统，基于回购契约考虑两阶段销售市场的情况，建立关于供应链利润的分散决策模型和集中决策模型，为供应商的库存和零售商的订货提供指导建议。

1 符号说明与基本假设

考虑由单一供应商G与单一零售商L、顾客群K组成的供应链系统。供应商与零售商的决策存在分散决策和集中决策两种情况，顾客群K存在策略型消费者，存在心理价格。零售商销售的产品与供应商供应的产品是同一产品，所面临的需求是相互独立的，销售的产品具有阶段性，并且是单期的。供应链成员的具体关系如图1所示：

1.1 符号说明

c：单位产品生产成本；a：单位产品批发价格；b：单位产品回购价；P1：第一阶段产品单位销售价格；P2：第二阶段产品单位销售价格；r：消费者对产品的估价；α：销售季末单位残值；Q：订购量；Xi：第i阶段的需求量；∏：期望利润；y：第一阶段结束时的库存量。

图1 供应链成员关系图

1.2 基本假设

（1）订货初期零售商与供货商签订回购契约，即供应商以价格b对季末未销售的产品进行回购，分担风险。假设该供应链符合一般性，即α≤c≤a≤p，α≤b≤a。市场需求X是随机变量，并服从（0,d）的均匀分布，d为市场需求量的最大饱和量。F（x）和f（x）分别表示随机需求的分布函数和概率密度函数，其中F（x）连续可微，即F（x）=0。

（2）假设顾客群存在策略型消费者，消费对产品的估价为r。由于其对产品估价的差异，他们在价格P下的购买决策会有所不同，其中估价高的消费者愿意提前在第一阶段购买，相反估价低的消费者则更倾向于延迟到第二阶段购买，因此设β为第二阶段消费者购买比例。第一阶段购买产品的消费者得到效用为U1=r-P1，第二阶段购买产品的消费者得到效用为U2=β（ r-δ），若U1≥U2，那么消费者就会选择在第一阶段购买产品。本文通过判断消费者的购买效用来讨论顾客的购买阶段，具体如表1所示。

表1 顾客购买阶段分析表

（3）在分散决策中，零售商和供应商分别独立决策，决策目标为利润最大化；在集中决策中，将零售商和供应商考虑为一个整体进行决策，决策目标为供应链的利润。由于存在回购契约，不考虑季末缺货的情景，即d≥Q。本文中下标s代表供应商，r代表零售商，sc代表供应链。

2 模型构建

本文基于回购契约，站在零售商的角度研究订货量与利润之间的关系。零售商根据销售情况决定是否降价，以及何时降价，以期通过两阶段模型确定最优订货量，扩大市场占有率，进而增加企业利润，两阶段模型的具体流程如图2所示。

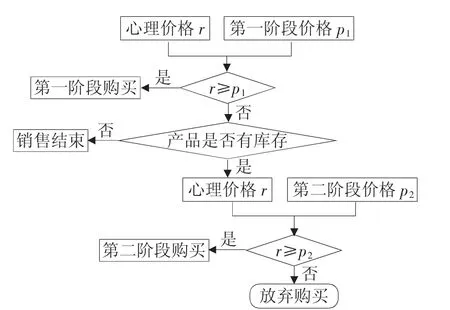
图2 两阶段模型流程图

根据图2可知，供应商、零售商以及整体供应链的利润模型为：

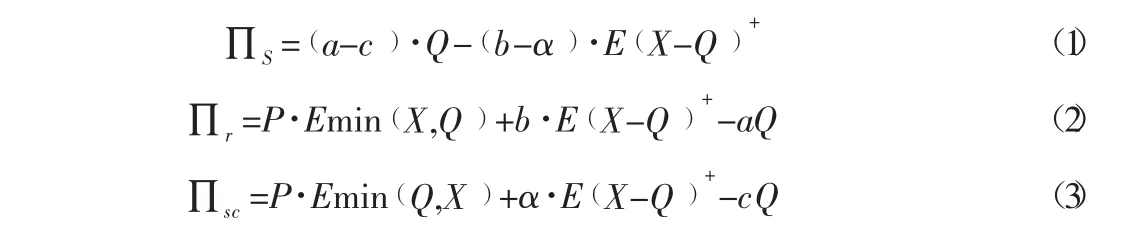
其中，（X-Q ）+表示未能出售的产品数量，且该数量只取大于零的结果；min（ X,Q ）表示市场实际需求量与订货量相比较，取较小的结果。因此，供应商的利润为产品批发价减去生产成本与季末未售出产品的回购价与残余价值之差；零售商的利润为实际需求量与订货量较小部分的收入加上未售出产品的回购收入减去产品批发价格；供应链的利润则为实际需求量与订货量较小部分的收入减去产品生产成本加上未售出产品的残余价值。

3 模型求解

3.1 集中决策模型求解

供应链协调就是以整条供应链利益为最优目标，进行集中决策。在集中决策模型中，供应商和零售商联合决策最优订货量，从而使得供应链利润最大化。根据公式（3）可知，供应链整体利润与汽车的订购量显著相关，因此，供应链的总期望利润本质上是由零售商的订货量决定的。在回购担保模式下，使得供应链整体利润最大化的最优订货量存在且唯一。

化简式 （3） 得：

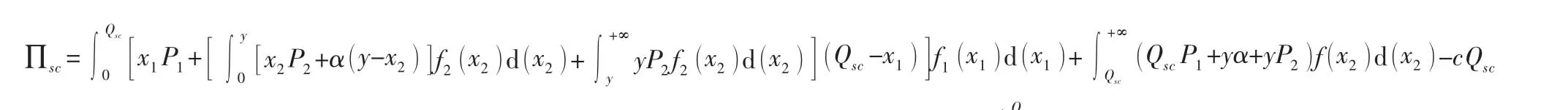
∏sc对Qsc一阶求导，并使一阶导数为0，可得：

因此，在回购担保模式下，集中决策的供应链总利润是关于订购量的凹函数，存在最小订货量，使得供应链利润最大化，即：

据所得结果可知，最优订货量与第二阶段产品价格、供应链的生产成本、市场需求量及销售期末未售出产品的残值相关。且供应链的生产成本越高，最优订货量就越低，供应链整体利润就越低；销售期末未售出产品残值越大，最优订货量越低，供应链的回购损失越低，收益就变得越大。

3.2 分散决策模型求解

在分散决策下，供应商和销售商只追求自身利润的最大化来进行决策，而不顾供应链的总利润是否最大化。供应商以批发价格a将产品批发给销售商，销售商分别以价格P1和P2在销售的两个阶段进行销售。销售商决定最优的订购量，使自身的利润能够最大化。

化简式（2）可得销售商的期望利润为：

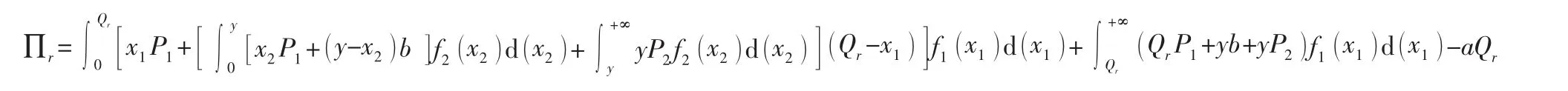
∏r对Qr一阶求导，并使一阶导数为0，可得：

因此，在回购担保模式下，分散决策的销售商总期望利润是关于订购量的凹函数，存在最小订货量，使得销售商利润最大化，即：

通过上述结果可以得出，销售商的最优订货量同产品价格、批发价格、市场需求量和回购价格之间有着密不可分的关系。产品的批发价格越高，零售商的最优订货量越小；回购价格越高，零售商的销售积极度下降，使得最优订货量下降。

化简式（1）可得供应商的期望利润为：

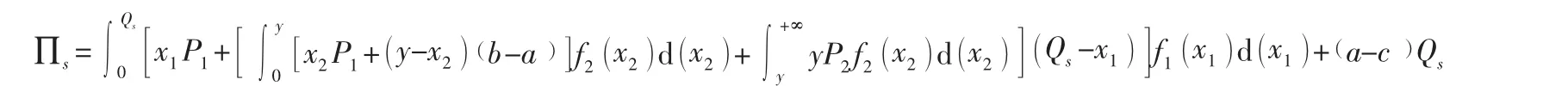
∏s对Qs一阶求导，并使一阶导数为0，可得：

因此，在回购担保模式下，分散决策的销售商总期望利润是关于订购量的凹函数，存在最小订货量，使得销售商利润最大化，即：

通过上述结果可以得出，最优订货量与产品批发价格、生产价格、回购价格、销售季末产品残值和市场需求量相关。产品的批发价格越高，最优订货量越小；回购价格越高，最优订货量越小，残值越高，最优订货量越小。

4 结论

本文研究了策略消费者异质情形下销售商的订货模型，将两阶段销售与回购契约相结合，分别考虑集中决策、分散决策的不同订货量情况。研究发现：批发价格和回购价格降低，可能导致零售商与供应商的订购量下降，进而使得利润减少；销售期末未售出产品残值越大，最优订货量越低，供应链的回购损失越低，收益就会变得越大。企业在销售产品时应加大宣传力度，尽最大程度地降低消费者放弃购买指数；同时要考虑批发价格和回购价格对零售商利润和供应商利润之间的冲突，尽最大程度地协调两者利益。供应商与零售商签订回购契约时一般都会预测此次销售的放弃购买指数，并签订一系列销售补偿措施，激励零售商的销售努力。本文仅考虑了两阶段销售情况，但是现实中商品的销售价格变动往往更加复杂，整个销售期内可能会出现多次降价的情况。因此，多阶段订货情况也是今后的研究方向。