构造函数在导数中的应用

■甘肃省白银市第一中学 胡贵平

构造函数是解导数问题的基本方法，怎样根据初等函数的导数公式和导数的基本运算法则，合理地构造出辅助函数，借助函数的性质，解决抽象函数的导数问题呢?下面举例说明。

类型一：f(x)+xf'(x)构造函数F(x)=xf(x)

例1(2018年甘肃兰州一诊)已知函数y=f(x)是定义域R上的偶函数，且当x＞0时，不等式f(x)+x·f'(x)＜0成立，若a=30.2f(30.2)，b=(logπ2)f(logπ2)，c=，则a，c，b之间的大小关系为( )。

A.a＞c＞b B.c＞a＞b

C.c＞b＞a D.b＞a＞c

解：记函数g(x)=xf(x)，则g'(x)=f(x)+xf'(x)，因为当x＞0时，不等式f(x)+x·f'(x)＜0成立，所以x＞0，g'(x)＜0，所以g(x)在(0，+∞)上单调递减，又因为函数y=f(x)是定义域R上的偶函数，所以函数g(x)=xf(x)为奇函数，且在R上单调递减，因为1＜30.2＜2，0＜logπ2＜1，log2=-2，所以-2＜logπ2＜30.2，所以c＞b＞a，故选C。

变式：nf(x)+xf'(x)构造函数F(x)=xnf(x)。

F(x)=xnf(x)，则F'(x)=nxn-1f(x)+xnf'(x)=xn-1[nf(x)+xf'(x)]。

例2(2009年天津文12)设函数f(x)在R上的导函数为f'(x)，且2f(x)+xf'(x)＞x2，下面的不等式在R内恒成立的是( )。

A.f(x)＞0 B.f(x)＜0

C.f(x)＞x D.f(x)＜x

解：由已知，首先令x=0得f(x)＞0，排除B，D。

令g(x)=x2f(x)，则g'(x)=x[2f(x)+xf'(x)]。

综上，f(x)＞0。故选A。

类型二：xf'(x)-f(x)构造函数F(x)

例3(2015年全国新课标Ⅱ卷理12)设函数f'(x)是奇函数f(x)(x∈R)的导函数，f(-1)=0，当x＞0时，xf'(x)-f(x)＜0，则使得f(x)＞0成立的x的取值范围是( )。

A.(-∞，-1)∪(0，1)

B.(-1，0)∪(1，+∞)

C.(-∞，-1)∪(-1，0)

D.(0，1)∪(1，+∞)

解：记函数g(x)=，则g'(x)=因为当x＞0时，xf'(x)-f(x)＜0，故当x＞0时，g'(x)＜0，所以g(x)在(0，+∞)上单调递减。又因为函数f(x)(x∈R)是奇函数，故函数g(x)是偶函数，所以g(x)在(-∞，0)上单调递减，且g(-1)=g(1)=0。当0＜x＜1时，g(x)＞0，则f(x)＞0;当x＜-1时，g(x)＜0，则f(x)＞0。综上所述，使得f(x)＞0成立的x的取值范围是(-∞，-1)∪(0，1)，故选A。

变式：xf'(x)-nf(x)构造函数F(x)

例4(2017年安徽省蚌埠二中等四校联考)定义在区间(0，+∞)上的函数f(x)满足:2f(x)＜xf'(x)＜3f(x)对x∈(0，+∞)恒成立，其中f'(x)为f(x)的导函数，则( )。

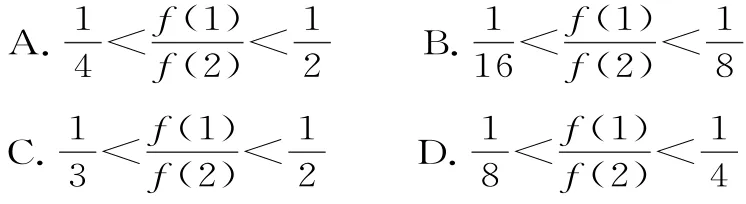
类型三：f'(x)+f(x)构造函数F(x)=f(x)ex

例5设f(x)是R上的可导函数，且f'(x)≥-f(x)，f(0)=1，f(2)=。则f(1)的值为____。

解：由f'(x)≥-f(x)得f'(x)+f(x)≥0，所 以 exf'(x)+exf(x)≥0，即[exf(x)]'≥0。设函数F(x)=exf(x)，则此时有1=F(2)≥F(0)=1，故F(x)=exf(x)=1，f(1)=。

变式：f'(x)+nf(x)构造函数F(x)=enxf(x)。

F(x)=enxf(x)，F'(x)=f'(x)enx+nenxf(x)=enx[f'(x)+nf(x)]。

例6已知函数f(x)满足:f(x)+2f'(x)＞0，那么下列不等式成立的是( )。

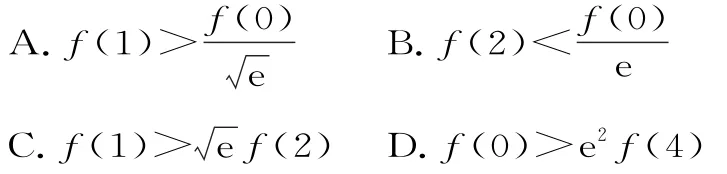
解：设F(x)=f(x)。

因为f(x)+2f'(x)＞0，所以F'(x)＞0，则F(x)在定义域上单调递增，所以F(1)＞F(0)，则，故答案为A。

类型四：f'(x)-f(x)构造函数F(x)=

例7(2017年南昌市三模)已知函数f'(x)是函数f(x)的导函数，f(1)=，对任意实数x，都有f(x)-f'(x)＞0，则不等式f(x)＜ex-2的解集为( )。

A.(-∞，e) B.(1，+∞)

C.(1，e) D.(e，+∞)

解：令 g(x)=，则g'(x)=

对任意实数x，都有f(x)-f'(x)＞0，所以g'(x)＜0，从而g(x)为R上的减函数。，即g(x)＜g(1)。因为g(x)为R上的减函数，所以x＞1，所以不等式f(x)＜ex-2的解集为(1，+∞)。故选B。

变式：f'(x)-nf(x)构造函数F(x)=

例8若定义在R上的函数f(x)满足f'(x)-2f(x)＞0，f(0)=1，则不等式f(x)＞e2x的解集为____。

解：令 g(x)=则g'(x)=

函数f(x)满足f'(x)-2f(x)＞0，所以g'(x)＞0，所以g(x)在R上单调递增，又f(0)=1，所以g(0)=1，不等式f(x)＞e2x可化为＞1，即g(x)＞g(0)，所以x＞0。故不等式f(x)＞e2x的解集为｛x x＞0｝。

类型五：f'(x)sinx +f(x)cosx构造函数F(x)=f(x)sinx

例9(2018届高三福建省德化永安漳平三校联考)定义在（ 0 ，）上的函数f(x)，f'(x)是它的导函数，且恒有cosx·f(x)+f'(x)sinx＞0成立，则( )。

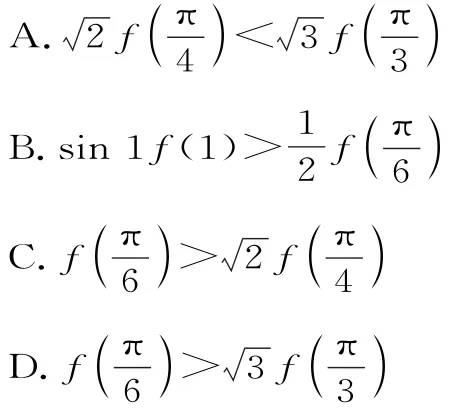
解：令g(x)=f(x)sin则g'(x)=cosxf(x)+f'(x)sinx＞0，从而g(x)在（ 0 ，）上单调递增，所以g(1)＞故选B。

类型六：f'(x)sinx-f(x)cosx构造

函数F(x)=

例10定义在（0 ，）上的函数f(x)，f'(x)是它的导函数，且恒有f(x)＞f'(x)·tanx成立，则( )。

解：因为x∈ （0 ，），所以sinx＞0，cosx＞0。由f(x)＞f'(x)tanx，得f(x)·cosx-f'(x)sinx＞0。

类型七：f'(x)cosx-f(x)sinx构造函数F(x)=f(x)cosx

若令F(x)=f(x)cosx，则F'(x)=f'(x)cosx-f(x)sinx。

例11设函数f'(x)是定义在(0，2π)上的函数f(x)的导函数，f(x)=f(2πx)。当 0＜x＜π 时，f(x)sinxf'(x)cosx＜0，若a=，b=0，c=，则a，b，c之间的大小关系为( )。

A.a＜b＜c B.b＜c＜a

C.c＜b＜a D.c＜a＜b

解：令g(x)=f(x)cosx，则g'(x)=f'(x)cosx-f(x)sinx＞0，所以函数g(x)在(0，π)上单调递增，因为f(x)=f(2πx)，所以g(x)=g(2π-x)，即g(x)的图像关于x=π对称，所以，所以a＜b＜c，故选A。

类型八：f'(x)cosx+f(x)sinx构造函数

例12(2018年湖南十校联考)已知函数y=f(x)对于任意的f'(x)cosx +f(x)sin x=1+lnx，其中f'(x)是函数f(x)的导函数，则下列不等式成立的是( )。

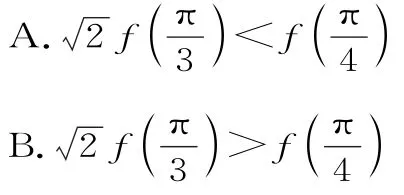
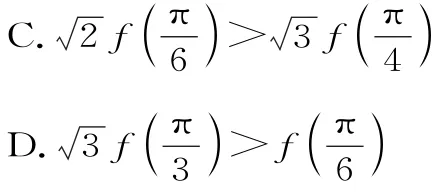
解：令则g'(x)=