定积分知识导学

■江苏省太仓高级中学 徐彩娥

定积分既是一个基本概念，又是一种基本思想。定积分的思想即“化整为零→近似代替→积零为整→取极限”。定积分这种“和的极限”的思想，在高等数学、物理、工程技术和其他的知识领域以及在人们生产实践活动中具有重要的意义，很多问题的数学结构与定积分中求“和的极限”的数学结构是一样的。教材通过对曲边梯形的面积、变速直线运动的路程等实际问题的研究，运用极限方法，经历分割整体、局部线性化、以直代曲、化无限为有限、变连续为离散等过程，使定积分的概念逐步发展建立起来。可以说，定积分最重要的功能是为我们研究某些问题提供一种思想方法(或思维模式)，即用有限的过程处理无限的问题，用离散逼近连续，以直代曲，局部线性化等。定积分的概念及微积分基本定理，不仅是数学史上，而且是科学思想史上的重要里程碑。定积分思想，是人类智慧的宝贵结晶，已成为人类文明中的财富。

让我们一起来学习定积分吧!

一、要点导学

1.相关术语

它表示函数f(x)与x轴，x=a，x=b围成的面积(x轴上方为正，x轴下方为负)和，所以只有当f(x)图像在区间[a，b]内完全位于x轴上方时，f(x)dx才表示面积。|f(x)|dx可表示函数f(x)与x轴，x=a，x=b围成的面积的总和，但是在求定积分时，需要拆掉绝对值，分段求解。

3.定积分的求法

(1)微积分基本定理:如果f(x)是区间[a，b]上的连续函数，并且F'(x)=f(x)，那

说明:使用微积分基本定理，关键是能够找到以f(x)为导函数的原函数F(x)。

所以常见的初等函数的导函数公式要熟记于心:

若f(x)=c，则f'(x)=0;

若f(x)=xα，则f'(x)=αxα-1;

若f(x)=sinx，则f'(x)=cos

x;

若f(x)=cosx，则f'(x)=-sin

x;

若f(x)=ax，则f'(x)=axlna;

若f(x)=ex，则f'(x)=ex;

若f(x)=logax ，则f'(x)=

①寻找原函数通常可以“先猜再调”，先根据导函数的形式猜出原函数的类型，再调整系数。例如导函数为f(x)=x3，则判断属于幂函数类型，其原函数应含x4，但(x4)'=4x3，而f(x)=x3，所以原函数应为F(x)=x4+c(c为常数)。

②如果只是求原函数，则要在表达式后面加上常数c，例如导函数为f(x)=2x，则原函数为F(x)=x2+c，但在使用微积分基本定理时，会发现计算F(b)-F(a)时会消去c，所以求定积分时，F(x)不需加上常数。

(2)利用定积分的几何含义:若被积函数找不到原函数，但定积分所对应的曲边梯形面积易于求解，则可通过求曲边梯形的面积求定积分。但要注意曲边梯形若位于x轴的下方，则面积与所求定积分互为相反数。

4.定积分的运算性质

作用:求定积分时可将f(x)的系数放在定积分外面，不参与定积分的求解，从而降低f(x)的复杂程度。

作用:可将被积函数拆成几个初等函数的和，从而便于寻找原函数并求出定积分，例如

作用:当被积函数含绝对值，或者是分段函数时，可利用此公式将所求定积分按区间进行拆分，分别求解。

5.利用定积分求曲边梯形面积的步骤

(1)通过作图确定所求面积的区域;

(2)确定围成区域中上，下曲线对应的函数f(x)，g(x);

(3)若x∈[a，b]时，始终有f(x)≥g(x)，则面积为

二、题型攻略

题型1 利用微积分基本定理求定积分

点评：一个函数的导数是唯一的，而其原函数则有无穷多个，这些原函数之间都相差一个常数，在利用微积分基本定理求定积分时，只需找到被积函数的一个原函数即可，并且一般使用不含常数的原函数，这样有利于计算。当被积函数无法直接找到原函数时，往往可以进行化简。

题型2 利用几何意义求定积分

例2已知函数f(x)=(x)dx=( )。

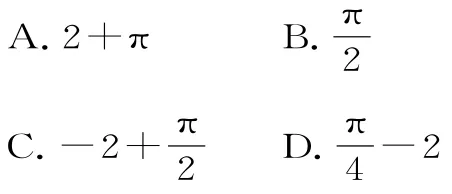
解 析：-2。

点评：(1)若被积函数在不同区间解析式不同时，则要考虑将定积分按不同区间进行拆分；

跟踪训练2(|x|+sinx)dx=____。

解析：。根据定积分的几何意义可知，函数y=|x|在[-1，1]上的图像与x轴，直线x=-1，x=1围成的曲边图形的面积为1。y=sinx为奇函数，根据定积分的几何意义知sinxdx=0。

题型3 已知定积分求参数的值

例3已知曲线y=x3与直线y=kx(k＞0)在第一象限内围成的封闭图形的面积为4，则k=。

图1

解析：联立方程可得解得x=0或x=。先根据题意画出图形，如图1所示，直线y=kx与曲线y=x3所围成图形的面积S=解得k=4，故答案为4。

点评：本题考查了曲线围成图形的面积，着重考查了定积分的几何意义和定积分计算公式等知识，属于基础题。用定积分求平面图形的面积的步骤：(1)根据已知条件，画出平面图形的草图；(2)根据图形特点，恰当选取计算公式；(3)解方程组求出每两条曲线的交点，以确定积分的上限、下限；(4)具体计算定积分，求出图形的面积。

跟踪训练3若18，则a=____。

解 析：+sinx）dx==18，解得a=3。

题型4 利用定积分求曲边图形的面积

例4已知函数f(x)=ex-1，直线l1:x=1，l2:y=et-1(t为常数，且0≤t≤1)，直线l1，l2，y轴与函数f(x)的图像围成的封闭图形如图2中阴影所示，当t变化时，阴影部分面积的最小值为____。

图2

解析：f(x)与直线l2的交点为:f(x)=et-1⇒ex-1=et-1，解得x=t。

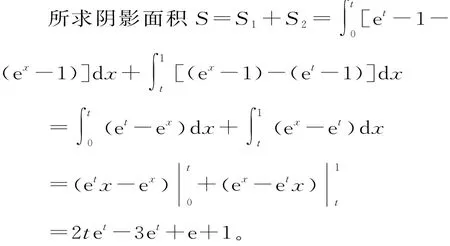
设S(t)=2tet-3et+e+1，则S'(t)=2tet-et=et(2t-1)。

min（-1）2。

点评：(1)本题是一道定积分与导数综合的题目，处理时要理解定积分和导数所起到的作用：定积分用于处理面积，而需要求函数最值时，可用导数解出单调性，从而求出最值。了解每个工具的作用才能在需要时选择正确的方法。

(2)对于含参数的定积分，首先要确定被积函数的自变量(可观察“d”后面的字母)，然后将参数视为一个常量参与运算即可，所得的结果通常是含参数的表达式。

跟踪训练4直线l过抛物线C:x2=4y的焦点且与y轴垂直，则直线l与抛物线C所围成的图形的面积等于____。

解析：抛物线C:x2=4y的焦点为(0，1)，故直线l的方程为y=1。

当y=1时，x=±2。