基于复杂网络的磁流变橡胶磁致压缩力学性能研究
2019-04-26柳彬游世辉赵树勋曾宪任
柳彬,游世辉,赵树勋,曾宪任
基于复杂网络的磁流变橡胶磁致压缩力学性能研究
柳彬,游世辉,赵树勋,曾宪任
(湘潭大学 土木工程与力学学院,湖南 湘潭 411105)
基于磁流变橡胶在机车的主动减振及降噪领域中的重要作用,引入复杂网络理论和方法来研究磁流变橡胶的磁致压缩力学性能。通过建立磁流变橡胶的RVE模型,利用多物理场耦合有限元软件研究磁流变橡胶的静态磁致压缩力学性能;计算磁流变橡胶的磁性颗粒复杂网络特征参数;探索磁流变橡胶磁性颗粒复杂网络的特征参数与磁流变橡胶磁致压缩模量之间的关系;与实例研究结果进行对比,验证结论的准确性。研究结果表明:磁流变橡胶的磁致压缩模量与其磁性颗粒网络的特征参数有关,其磁致压缩模量的峰值是由磁性颗粒的复杂网络分形特征参数决定的。
磁流变橡胶;复杂网络;磁致压缩模量;数值模拟;实验研究
磁流变橡胶(MR rubber)是由铁磁颗粒嵌入橡胶基体中制成的磁流变材料。相较于传统的橡胶材料,磁流变橡胶兼具了磁性颗粒和橡胶材料的优点,并且其力学和磁学性能可随外加磁场的强度变化而改变,因此广泛地应用于高速列车、铁路斜拉索桥、汽车和舰船等的主动减振及降噪等工程领域方面[1−2]。丁志华等[3]研究设计的磁流变橡胶空气弹簧可实时调节高度和刚度的问题,提高各类机车的减振性能,该设计已获得国家发明专利[4]。段富贵等[5−6]研究的磁流变橡胶的吸声与隔声性能可应用于吸声板和隔声板。近年来,磁流变橡胶的理论实验研究[7−9]已经相当成熟,在数值模拟方面,Lokander等[10]研究磁场强度和颗粒对磁流变橡胶的磁流变效应的影响,以及磁场对磁流变橡胶阻尼的影响。段富贵等[5−6]分别研究磁流变橡胶的吸声和隔声性能。Watts等[11−12]发表了研究复杂网络的特性的方法,掀起了复杂网络的研究热潮。Silva等[13]把网络理论运用到复合材料电导系数与网络障碍之间的关系中,论证了复杂网络可以应用于材料科学。Roberto等[14]研究了颗粒状材料接触网络的分形维数与力阈值的函数关系。段富贵等[5−6]将复杂网络应用到多孔橡胶材料的吸声与隔声性能与复杂网络参数的关联性的研究中。随着计算机技术的进步,现阶段可通过核磁共振成像技术或CT扫描技术获得磁流变橡胶细观结构。在细观尺度上,磁流变橡胶中的磁性颗粒形成磁弹耦合结构网络,并与基体的分子链网络相互作用,在整体上形成互相关联的结构网络系统。当在结构网络系统上施加耦合场时,系统会产生细观和宏观的磁弹性耦合和粘弹性效应,以及细观和宏观之间的相互作用的结构网络系统的演化[15]。在此基础上,本文提出引入复杂网络理论来描述细观尺度上的磁性颗粒结构网络系统,进而来描述磁流变橡胶的磁性颗粒网络与磁致力学性能之间的关联性。
1 复杂网络理论基础
复杂网络的研究基础是图论,即它是一个有着复杂拓扑结构特征的图。复杂网络特征的主要度量参数包括度分布,集聚系数、平均路径长度和分形维数。网络的度分布反映了整个网络拓扑的重要信息,它是指网络中任一个节点所具有的与其他节点相连接的边的数目,节点度分布用函数()来表示。网络的集聚系数[13]表示节点与k个相邻节点连接的紧密程度,可用公式表达为
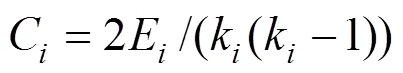
将2个节点连接起来的最短边数即为节点的距离,那么网络的平均路径长度则为任意2个节点之间的距离的平均值。分形维数是对复杂网络分形定量表征的重要参数,本文的磁性颗粒复杂网络分形维数采用LIU[16]提出的改进沙箱算法计算。
现阶段,能够描述接近真实世界特性的复杂网络模型主要为小世界网络和无标度网络模型[17]。在本文中磁性颗粒间作用并没有方向性,故选取构造无向无权网络模型。利用大型复杂网络分析软件Pajek对每个磁性颗粒随机编号,如图1所示,将每个磁性颗粒等效成一个节点,根据3-正则图的对偶图和邻近原则构造磁性颗粒复杂网络模型如图2所示。本文中复杂网络平均度、簇聚系数和平均最短路径的值,都是采用Pajek软件计算的。
为了便于计算机处理,网络图也可用矩阵表示。邻接矩阵是表示顶点之间相邻关系的矩阵,邻接矩阵可分为有向和无向邻接矩阵。对于本文中的无向网络而言,邻接矩阵一定是对称的,且主对角线一定为0,则图2的邻接矩阵的表示如式(2)。将邻接矩阵导入到MATLAB中根据改进的沙箱算法进一步计算出复杂网络的分形维数。

图1 磁性颗粒分布示意图
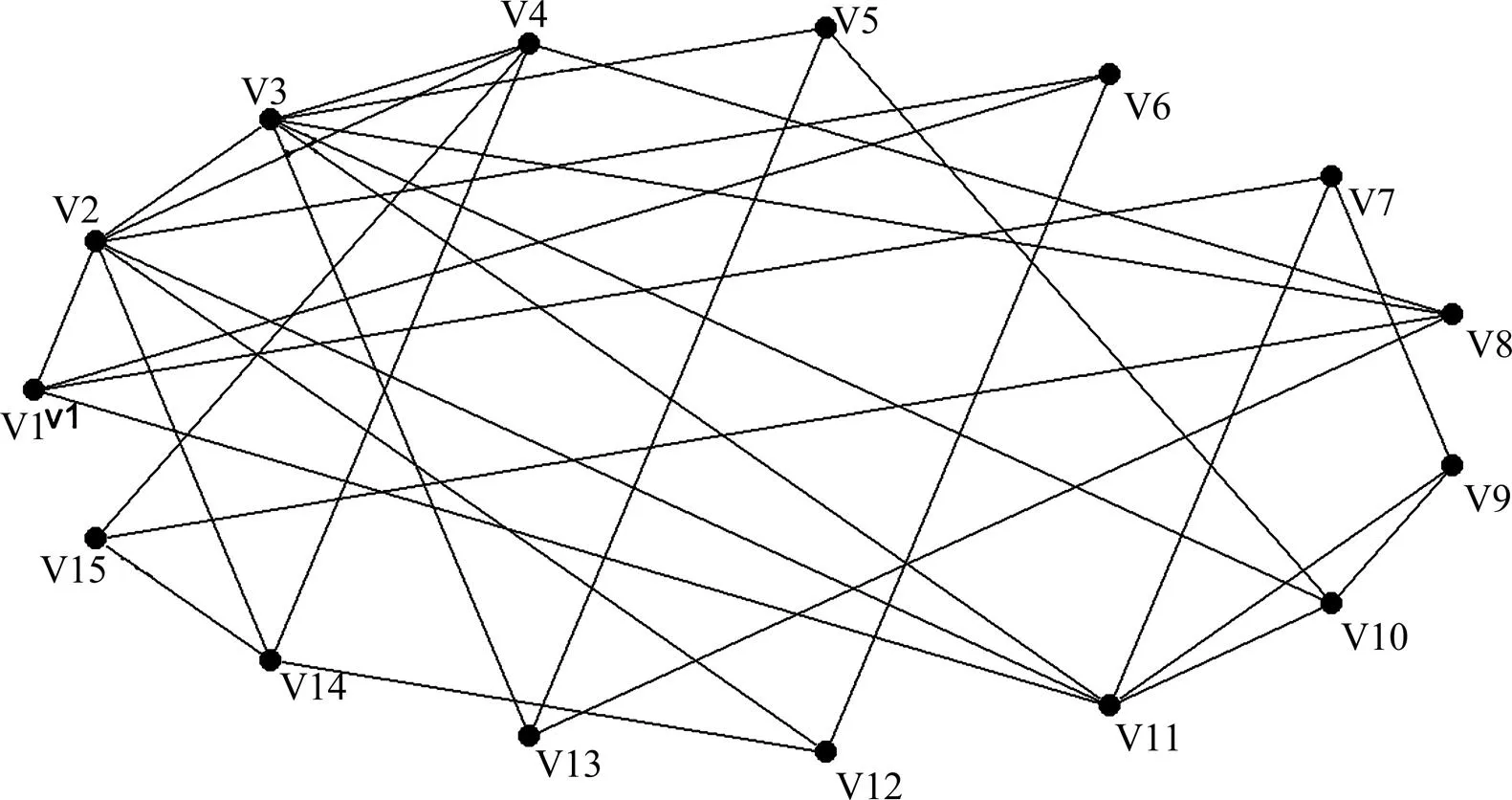
图2 磁性颗粒复杂网络模型

2 磁流变橡胶的磁致压缩力学性能研究
对于耦合场作用下的磁流变橡胶的数值模拟,需利用大型多物理场耦合软件COMSOL构建磁流变橡胶RVE模型,并施加周期性边界条件,设定耦合场的方向和强度如图3所示。该模型尺寸为20 μm×20 μm,颗粒直径介于3~5 μm。在磁性颗粒的边界用Maxwell应力张量施加磁场力,图4显示了磁场条件下磁流变橡胶RVE模型在压缩条件下的应力变形。
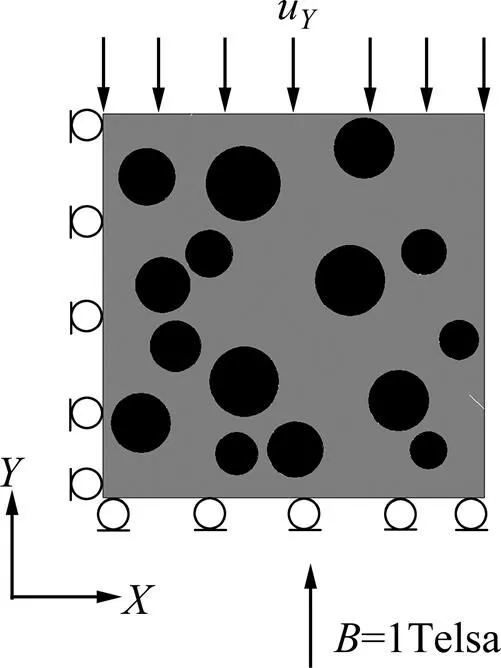
图3 磁流变橡胶压缩RVE模型
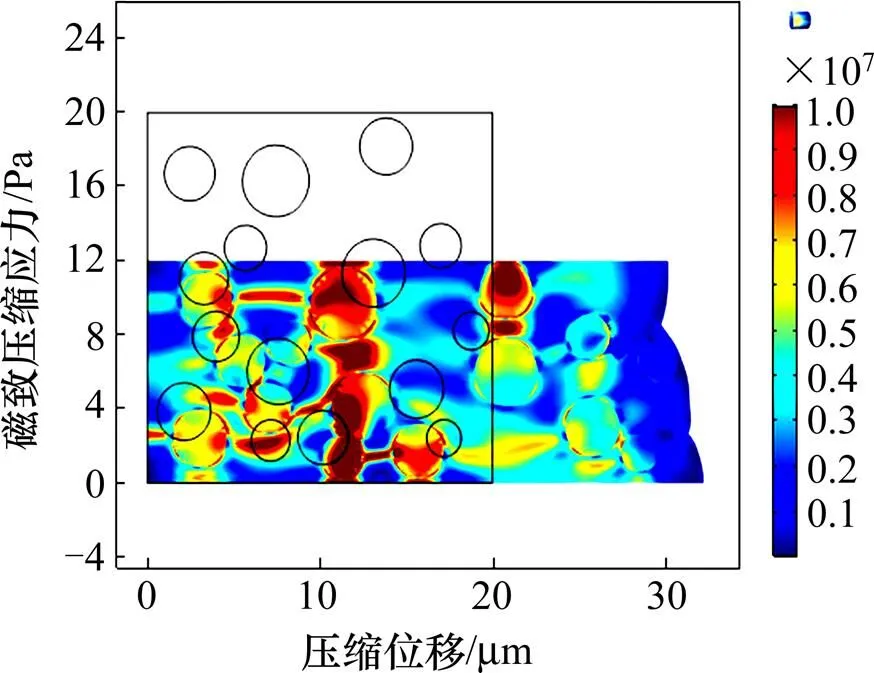
图4 各向同性磁流变橡胶压缩变形
图5显示了压缩条件下的磁性颗粒组分对磁流变橡胶的磁致力学性能的影响。磁流变橡胶的磁致压缩应力随体积分数的增加而增加。而磁性颗粒体积分数20%以上的磁致压缩应力值变化较明显。图6所示的磁流变橡胶磁致压缩模量与应变曲线关系是由将图5的曲线的斜率转换成的,随着磁性颗粒体积分数的增加,磁流变橡胶的磁致压缩模量逐渐增大。当磁性颗粒体积分数增至25%时,磁性颗粒组分对磁流变橡胶的磁致压缩模量的影响较为 显著。
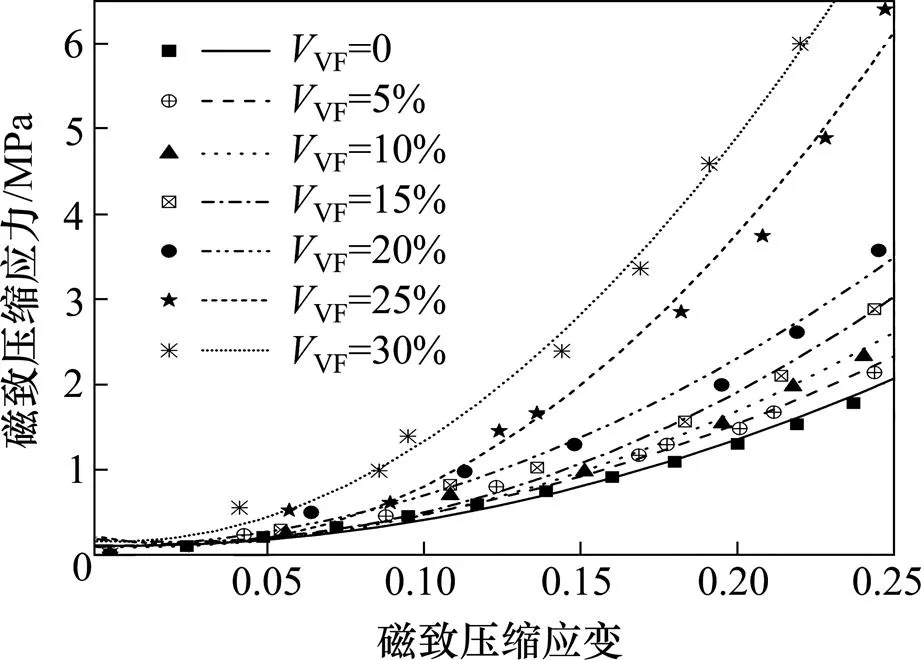
图5 磁流变橡胶的磁致压缩应力-应变曲线
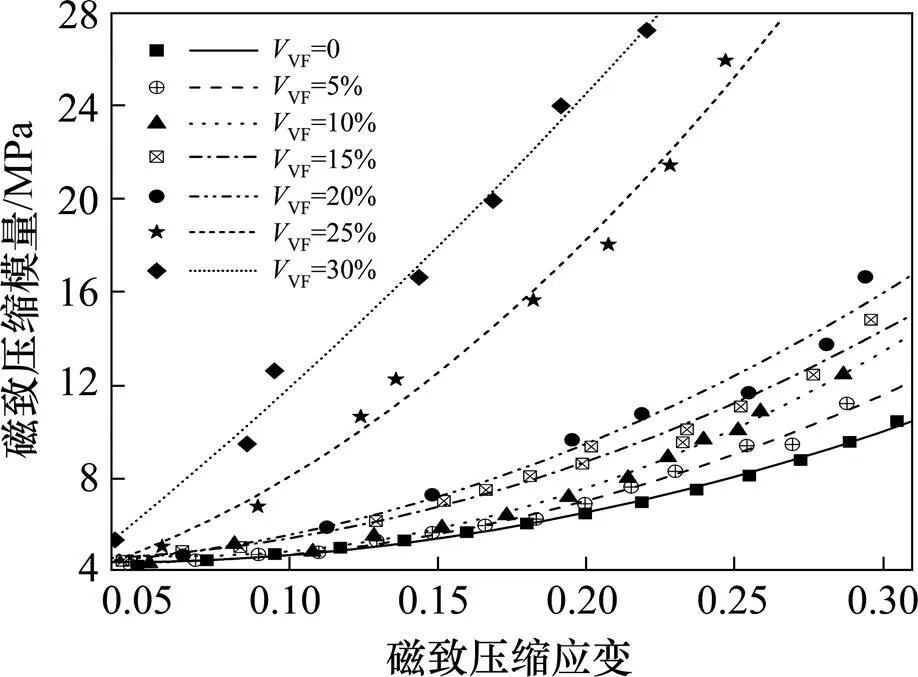
图6 磁流变橡胶磁致压缩模量-应变曲线
磁致压缩模量的影响因素众多,本文除了研究磁性颗粒组分对磁流变橡胶的磁致压缩模量的影响外,还将探讨磁场强度对压缩条件下磁流变橡胶磁致模量的影响。
图7显示了磁场强度对磁流变橡胶磁致压缩力学性能的影响。结果表明磁流变橡胶的磁致压缩应力随外部磁场强度增大而增加。而磁场强度对磁流变橡胶压缩模量的影响如图8所示。在小变形条件下,磁流变橡胶磁性颗粒体积分数小于10%时,外部磁场对磁流变橡胶磁致压缩模量几乎没有影响。当磁流变橡胶磁性颗粒体积比大于15%时,磁场强度对磁流变橡胶磁致压缩模量的影响逐步增大。以上数值模拟结果已在文献[18]与实验数据对比 研究。
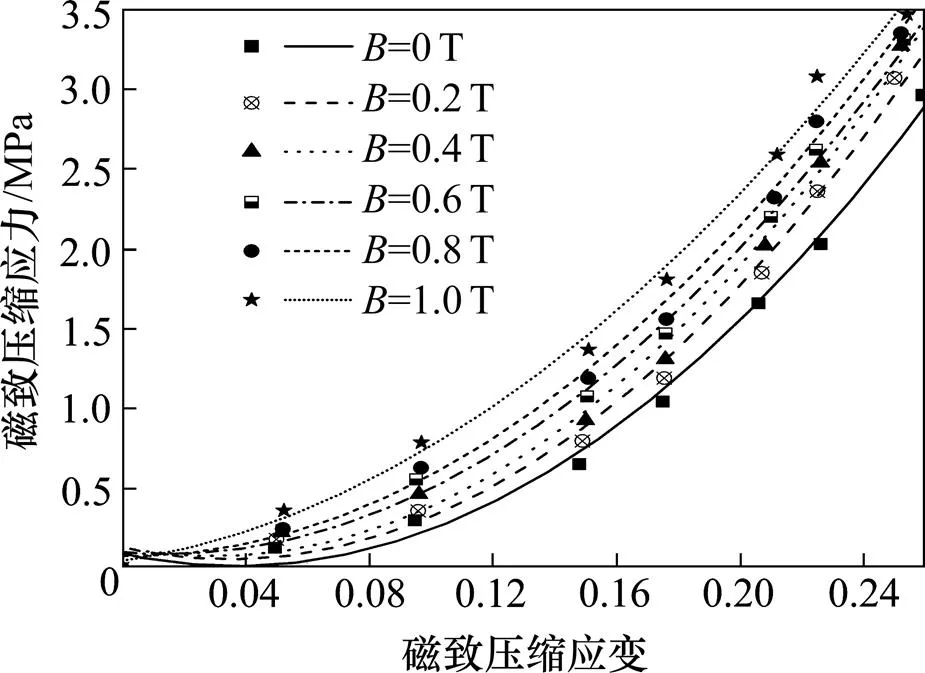
图7 磁流变橡胶磁致压缩应力-应变曲线

图8 磁流变橡胶的磁致压缩模量-颗粒体积分数曲线(%)
3 磁流变橡胶磁性颗粒复杂网络特性
在复杂网络系统上施加耦合场时,网络系统会产生细观和宏观的磁弹性耦合效应,而复杂网络就承担起构建宏观力学性能与细观拓扑结构特性的桥梁。本节利用复杂网络的特征参数来构建细观网络结构特征与宏观磁流变橡胶的磁性颗粒体积分数的基本规律。
研究结果如图9~12所示。图9显示了各向同性磁流变橡胶磁性颗粒网络的度值分布情况,从图中可以看出磁性颗粒网络的平均度值随磁性颗粒体积分数的增大而增大,最后趋近于平稳。而磁性颗粒网络集聚系数的分布情况图10所示,磁性颗粒网络的集聚系数随体积分数的增大而减小,最终趋近于平稳。图11中的磁性颗粒网络平均最短路径值则随体积分数的增大而增大,曲线接近线性关系。磁流变橡胶磁性颗粒网络的分形维数随磁性颗粒体积分数的增长先迅速增加,而后在某个区域上下波动,有接近平稳的趋势,如图12所示。

图9 磁流变橡胶磁性颗粒网络的平均度-体积分数(100%)

图10 磁流变橡胶颗粒网络的集聚系数-体积分数(100%)
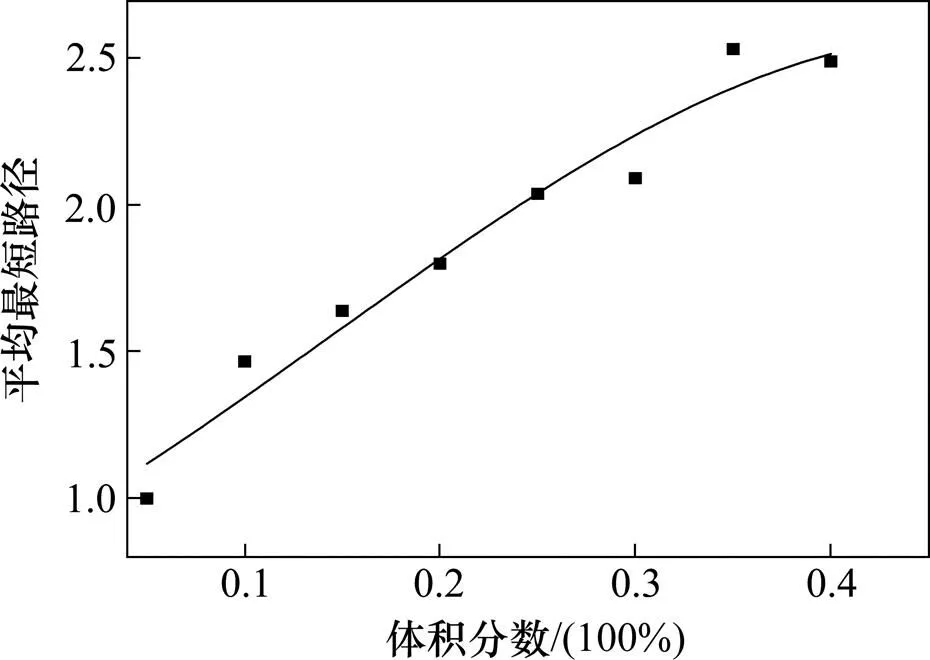
图11 磁流变橡胶颗粒网络的平均最短路径-体积分数(100%)
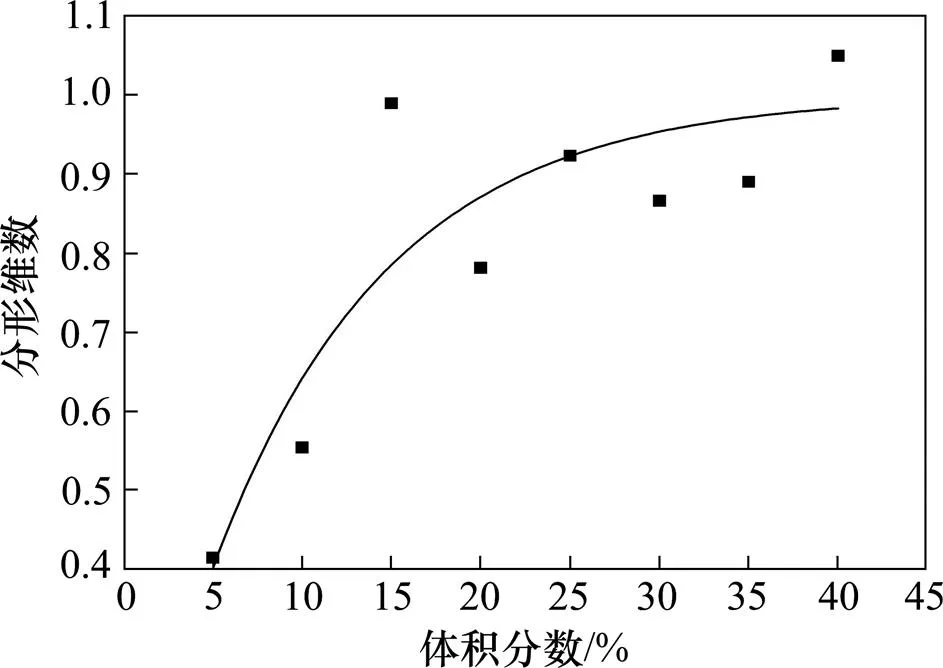
图12 磁性颗粒体积分数(%)-磁性颗粒网络分形维数曲线
4 磁流变橡胶的磁致力学性能与磁性颗粒网络特征分析
本文分别研究磁流变橡胶的磁致压缩模量、磁流变橡胶的磁性颗粒复杂网络参数与磁性颗粒组分关系,本节则研究磁流变橡胶的磁致力学性能与磁性颗粒复杂网络参数的关联性。
分别将图9~12与图8进行转换,得到压缩条件下磁流变橡胶的磁致力学参数与磁性颗粒复杂网络参数的关系曲线,结果如图13~16所示。图13中磁流变橡胶的磁致压缩模量值随磁性颗粒网络平均度的增加而增大;当磁性颗粒网络的平均度大于3时,磁致压缩模量的变化开始明显。图14中磁流变橡胶磁致压缩模量随磁性颗粒网络平均集聚系数的增加而逐渐减小;当平均集聚系数大于0.8时,磁致压缩模量几乎不随平均集聚系数而变化。图15显示了磁流变橡胶磁性颗粒网络的平均最短路径长度与磁致压缩模量之间的关系,总体上,磁流变橡胶的压缩模量值随平均最短路径长度的增加而增大;但当平均最短路径长度小于1.5时,磁流变弹性体的磁致压缩模量几乎不受外部磁场的影响。在图16中,磁流变橡胶的磁致压缩模量随磁性颗粒网络的分形维数增加而先增大后减小;磁流变橡胶磁致压缩模量的峰值处的分形维数对应的磁性颗粒体积分数介于25%~30%之间,与现有实验研究[9]结果吻合。

图13 磁性颗粒网络的平均度-磁致压缩模量曲线
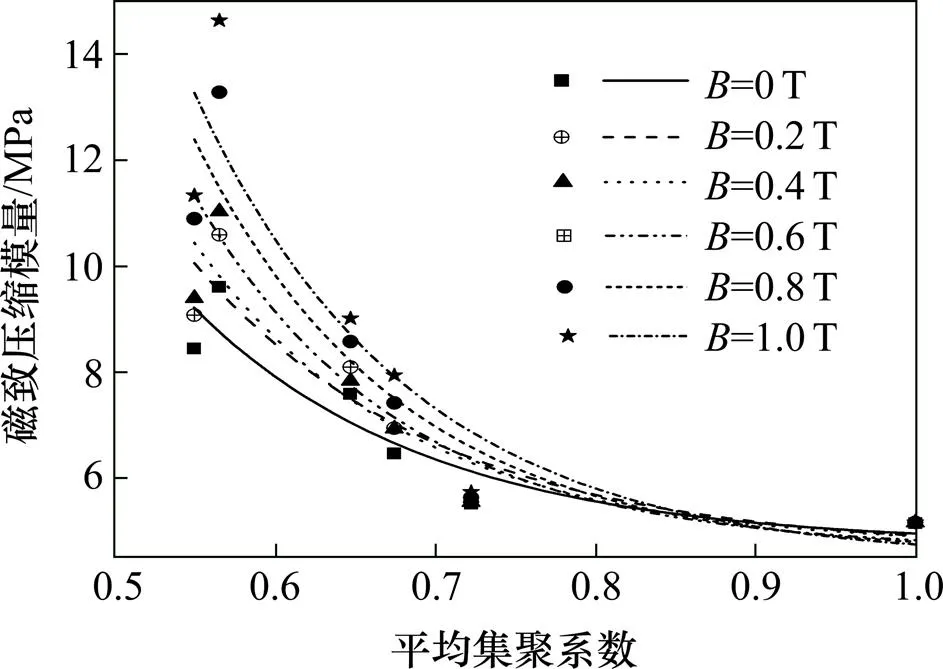
图14 磁性颗粒网络的平均集聚系数-磁致缩模量曲线
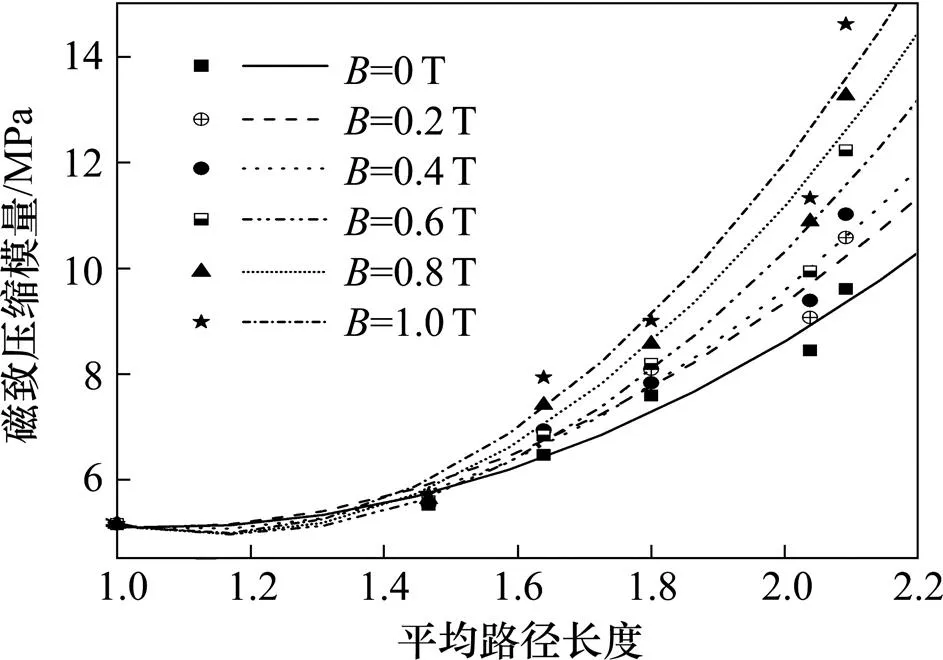
图15 磁性颗粒网络的平均路径长度-磁致压缩模量曲线
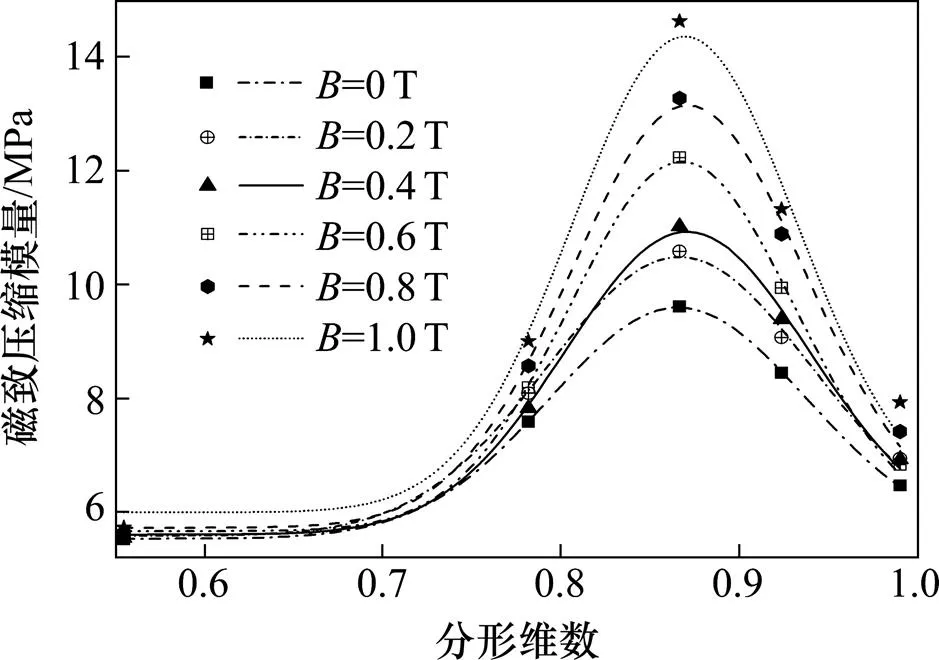
图16 磁性颗粒网络分形维数-磁致压缩模量曲线
5 磁流变橡胶的实验研究
实验制备磁流变橡胶所用的球形羟基铁粉颗粒的平均尺寸为3~5 μm,电镜照片见图17。在制备磁流变橡胶时,先干燥羟基铁粉,然后逐步将羰基铁粉与硅油混合确保铁磁颗粒分布均匀且不粘连,再加入到橡胶中搅拌均匀。将均质的铁粉橡胶混合物倒入平面模具中开模,脱气。再在液压机中固化。以同样的方法制备球形羟基铁粉体积比为5%~30%的磁流变橡胶样品。用扫描电子显微镜SEM和光学显微镜检查实验制备样品的SEM表面如图18所示。

图17 羰基铁粉的SEM形貌
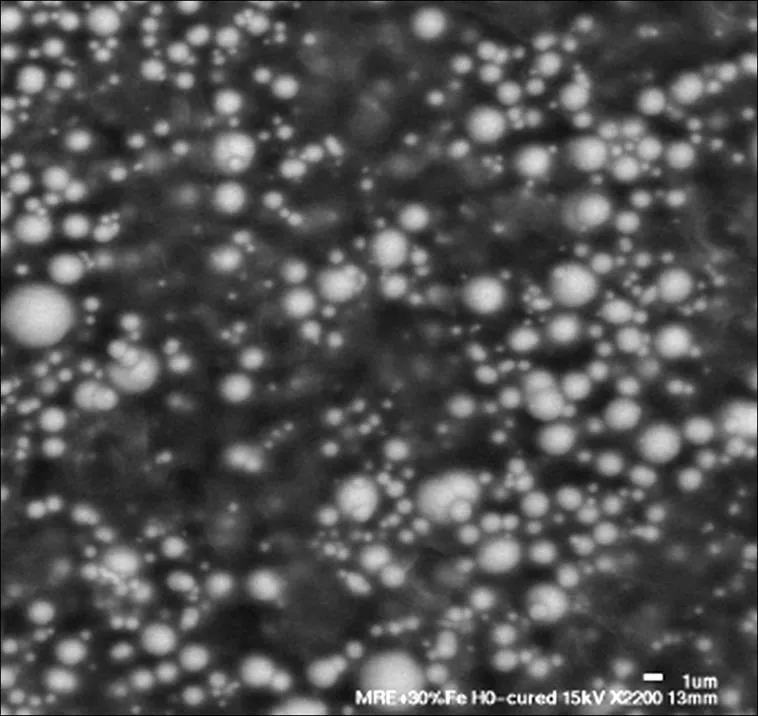
图18 各向同性磁流变橡胶样本断裂表面SEM形貌
准备羟基铁粉体积比为30%的磁流变橡胶材料样本进行压缩测试,用于压缩测试的磁流变橡胶样本如图19。磁流变橡胶的静态压缩测试结果以及实验与数值模拟结果对比可参考文献[18],本章直接研究实验制备磁流变橡胶的复杂网络特性。在计算实验制备磁流变橡胶的复杂特性之前,需将样本SEM图像通过图形图像转换技术[19]转换成可直接导入有限元软件中计算的矢量图,在转换中,排除相交的磁性颗粒,只选取最上层的磁性颗粒,得到磁流变橡胶矢量图如图20所示。任意选取20 μm× 20 μm细观局部结构图如图21。
在计算实验制备的磁流变橡胶样本的复杂网络特性时,需要借助Pajek构建接近真实的复杂网络模型,并对磁性颗粒的复杂网络参数进行处理。将实验制备的磁流变橡胶的磁性颗粒复杂网络参数与数值模拟结果对比可得到图22~25。对于复杂网络的4个参数:平均度、平均集聚系数、平均最短路径和分形维数,虽然数值模拟结果与实验数据有细微的差别,但各参数与体积分数曲线的发展趋势是一致的,验证了数值模拟结果的正确性。

图19 磁敏橡胶压缩测试样本

图20 各向同性磁流变橡胶样本二维矢量图

图21 磁流变橡胶样本局部细观图

图22 平均度与颗粒体积分数(%)的模拟与实验数据对比

图23 平均集聚系数与颗粒体积分数(%)的模拟与实验数据对比
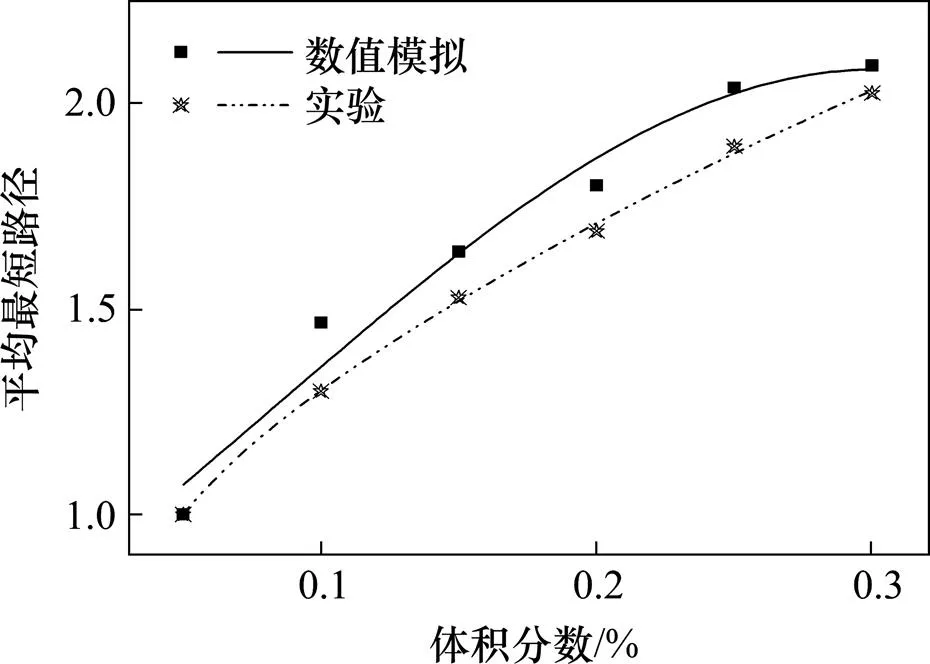
图24 平均最短路径与颗粒体积分数(%)的模拟与实验数据对比

图25 分形维数与颗粒体积分数(%)的模拟与实验数据对比
6 结论
1) 磁流变橡胶的磁致压缩模量可以通过磁性颗粒复杂网络特征参数来定性描述。通过磁流变橡胶的细观结构特征,估算磁流变橡胶的宏观力学性能。
2) 磁流变橡胶的磁致压缩模量的峰值只与磁性颗粒网络的分形维数有关,而与磁场强度大小无关。即可通过磁流变橡胶的复杂网络分形维数确定磁性颗粒的最佳体积比。本文中的磁性颗粒最佳体积比介于25%~30%之间,与已有的研究结果相 吻合。
[1] 刘少谦. 磁流变橡胶减振器的设计与研究[D]. 厦门: 华侨大学, 2008. LIU Shaoqian. Design and research of magnetorheological rubber shock absorber[D]. Xiamen: Huaqiao University, 2008.
[2] 孙航, 高秀云, 陈大鹏. 基于碳纳米管加强的磁流变橡胶支座在连续梁桥减隔震中的应用分析[EB/OL]. http:// www.paper.edu.cn/releasepaper/content/201401[2014−01 −26]. SUN Hang, GAO Xiuyun, CHEN Dapeng. Application analysis of magnetorheological rubber support based on carbon nanotubes in seismic reduction of continuous beam bridges[EB/OL]. http://www.paper.edu.cn/release epaper/content/201401[2014−01−26].
[3] 丁志华, 游世辉. 磁流变弹性体橡胶空气弹簧的结构设计[J]. 机械设计与制造, 2008(10): 17−18. DING Zhihua, YOU Shihui. Structural design of magnetorheological elastomeric rubber air spring[J]. Mechanical Design & Manufacture, 2008(10): 17−18.
[4] 游世辉, 肖静, 冯云华, 等. 一种磁流变液压橡胶弹簧: 中国, 201010508586.4[P]. 2014−12−10. YOU Shihui, XIAO Jing, FENG Yunhua, et al. A magnetorheological hydraulic rubber spring: China, 201010508586.4[P]. 2014−12−10.
[5] 段富贵. 磁流变橡胶材料隔声性能数值模拟[D]. 湘潭:湘潭大学, 2017. DUAN Fugui. Numerical simulation of sound insulation performance of magnetorheological rubber material[D]. Xiangtan: Xiangtan University, 2017.
[6] 杨罡星. 磁流变橡胶材料吸声性能数值模拟[D]. 湘潭:湘潭大学, 2017. YANG Gangxing. Numerical simulation of sound absorption properties of magnetorheological rubber materials[D]. Xiangtan: Xiangtan University, 2017.
[7] 孙友谊. 磁流变橡胶材料的研究现状[R]. 国家自然基金委员会、扬州大学、北京市新型高分子材料制备加工成型重点实验室、中国化工学会橡胶专业委员会, 2016: 1. SUN Youyi. Research status of magnetorheological rubber materials[R]. National Natural Science Foundation of China, Yangzhou University, Beijing Key Laboratory of New Polymer Material Preparation, Processing and Molding, China Rubber Industry Committee, 2016: 1.
[8] 游世辉. 磁敏橡胶力学性能的研究与应用[D]. 广州: 华南理工大学, 2008. YOU Shihui. Research and application of mechanical properties of magnetic resin[D]. Guangzhou: South China University of Technology, 2008.
[9] Ioan Bicaa, Eugen M Anitas, Madalin Bunoiuc, et al. Hybrid magnetorheological elastomer: Influence of magnetic field and compression pressure on its electrical conductivity[J]. Journal of Industrial and Engineering Chemistry, 2014, 20(6): 3994−3999.
[10] Lokander M, Stenberg B. Improving the magnet- orheological effect in isotropic magnetorheological rubber materials[J]. Polymer Testing, 2003, 22(6): 677− 680.
[11] Watts D J, Strogatz S H. Collective dynamics of small world networks[J]. Nature, 1998(393): 440−442.
[12] Barabási A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999(286): 509−512.
[13] Silva J, Simoes R, Lanceros-Mendez S, et al. Applying complex network theory to the understanding of high-aspect-ratio carbon-filled composites[J]. Euro Physics Letters, 2011, 93(3): 37005.
[14] Roberto Arévalo, Iker Zuriguel, Diego Maza. Topological properties of the contact network of granular materials[J]. International Journal of Bifurcation & Chaos, 2009, 19(2): 695−702.
[15] 张波. 复杂网络的构建及演化方式研究[D]. 长春: 吉林大学, 2014. ZHANG Bo. Research on the construction and evolution of complex networks[D]. Changchun: Jilin University, 2014.
[16] LIU J L, YU Z G, Anh V. Determination of multifractal dimensions of complex networks by means of the sandbox algorithm[J]. Chaos, 2015, 25(2): 392−395.
[17] 孙玺菁, 司守奎. 复杂网络算法与应用[M]. 北京: 国防工业出版社, 2015. SUN Xijing, SI Shoukui. Complex network algorithm and application[M]. Beijing: Defense Industry Press, 2015.
[18] 柳彬, 游世辉, 赵树勋, 等. 基于Digimat中RVE模型的磁流变弹性体的磁致压缩力学性能的数值模拟[J].功能材料, 2018, 49(2): 67−75. LIU Bin, YOU Shihui, ZHAO Shuxun, et al. Simulation of magnetic field induced compressive mechanical properties of magneto-rheological elastomers based on RVE model in Digimat[J]. Functional Materials, 2018, 49(2): 67−75.
[19] 宋欢. 基于图形图像转换的磁流变弹性体拉伸力学性能的数值模拟[D]. 湘潭: 湘潭大学, 2017. SONG Huan. Numerical simulation of tensile mechanical properties of magnetorheological elastomer based on graphical image transformation[D]. Xiangtan: Xiangtan University, 2017.
Research on magneto-rheological rubber compression mechanical properties based on complex network
LIU Bin, YOU Shihui, ZHAO Shuxun, ZENG Xianren
(College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China)
Magneto-rheological rubber plays an important role in the field of active vibration and noise reduction of locomotives. This paper aims to introduce complex network theory and methods to study the magneto-induced compression mechanical properties of magneto-rheological rubber. By establishing the RVE model of magneto-rheological rubber, the static magneto-induced compressive mechanical properties of magneto- rheological rubber were simulated using COMSOL multiphysics software. And the topological structure and fractal characteristics of the complex network of magnetic particles were studied. Finally, the association of the magneto-induced compression mechanical properties and complex network parameters was explored. And the results of the simulation study were compared with the experimental study data to verify the accuracy of the conclusions. The results show that the magneto-induced modulus of magneto-rheological rubber is related to the characteristic parameters of the magnetic particles network, and the peak value of magneto-induced modulus is determined by the fractal characteristic parameters.
magneto-rheological rubber; complex network; magneto-induced compressive modulus; numerical simulation; experimental study
10.19713/j.cnki.43−1423/u.2019.04.027
TB381
A
1672 − 7029(2019)04 − 1041 − 09
2018−05−27
国家自然科学基金资助项目(51375416);湖南省教育厅创新平台开放基金资助项目(15K131)
游世辉(1962−),男,江西萍乡人,教授,博士,从事工程中的力学问题与计算研究;E−mail:shihuiyou@hotmail.com
(编辑 蒋学东)
