铁路桥上减振CRTS-Ⅲ型无砟轨道振动响应及车辆平稳性分析
2019-04-26宋瑞刘林芽徐斌曾开华
宋瑞,刘林芽,徐斌,曾开华
铁路桥上减振CRTS-Ⅲ型无砟轨道振动响应及车辆平稳性分析
宋瑞1, 2,刘林芽2,徐斌1,曾开华1
(1. 南昌工程学院 土木与建筑工程学院,江西 南昌 330029; 2. 华东交通大学 铁路环境振动与噪声教育部工程研究中心,江西 南昌 330013)
为了研究桥上减振CRTS-Ⅲ型无砟轨道对车体系统和轨道系统振动影响,分析车辆的平稳性指标,基于车辆、轨道系统二维模型,利用动柔度法分别计算车辆、轨道系统的动柔度,建立频率域的车辆-轨道-桥梁耦合模型;计算车辆及轨道系统的振动加速度并分析其规律,计算不同轨道系统下车辆的平顺性指标。研究结果表明:与常规CRTS-Ⅲ型轨道相比,采用橡胶减振垫刚度为0.018 N/m3的减振轨道系统下峰值轮轨力减小,车轮、转向架振动加速度分别降低13.6%和52.6%,车体在1~20 Hz范围内振动变化不大;钢轨、轨道板的振动加速度增大1.69和2.68倍,桥梁的振动加速度减少69.9%;车辆的平顺性指标分别为2.70和2.61,车辆平稳性指标降低4%。与常规CRTS-Ⅲ型无砟轨道相比,减振CRTS-Ⅲ型无砟轨道下车辆系统各构件的振动加速度有不同程度的降低,轨道系统中,钢轨和轨道的振动加速度增大,桥梁振动加速度降低。车辆的平稳性指标降低,乘客的舒适性有一定程度提高。
铁路桥梁;减振CRTS-Ⅲ型轨道;振动;平顺性
随着我国高速铁路的快速发展,无砟轨道技术已广泛应用于我国的高速铁路中。其中常用的CRTS-Ⅰ型和CRTS-Ⅱ型轨道系统是我国在充分吸收日本和德国技术的基础上开发的,不具备完全自主知识产权。CRTS-Ⅲ型轨道系统是我国具有完全自主知识产权的无砟轨道系统,主要由钢轨、扣件、混凝土轨道板、自密实混凝土、土工布、底座等结构部件组成,目前已广泛应用于郑徐、京沈、商合杭等16条高速铁路,是我国高铁“走出去”采用的主要轨道形式。与常规CRTS-Ⅲ型轨道系统相比,减振CRTS-Ⅲ型轨道系统是在自密实混凝土和底座板板间采用橡胶减振垫层隔离,具有隔振效果好,成本低等特点。我国最早在成灌快速铁路开展了一系列关于减振垫的研究。赵才友等[1]对铺设橡胶减振垫区段和未铺设减振区段的路基段和桥梁段进行仿真计算和现场实测,结果表明采用减振垫能有效降低桥梁结构和地面的振动加速度,但轨道板和钢轨的振动加速度有一定的增大。辛涛等[2]采用谐响应分析方法,探讨减振垫设置在不同位置时对钢轨、轨道板和路基导纳的影响,采用车辆-轨道耦合方法,分析列车高速通过时轨道系统的动力影响。任娟娟等[3]以减振CRTS-Ⅲ型轨道为研究对象,建立二维轨道频域分析模型研究其频域内振动传递特性,分析隔振效率并提出合适的轨道结构参数。周毅[4]分析10~1 000 MPa/m范围内不同减振垫刚度条件下钢轨、轨道板、桥梁的加速度和位移,确定了扣件和减振垫层的合理刚度范围。ZHAO等[5]针对成灌快速铁路铺设减振垫区段和未铺设区段的列车车内振动、噪声,轨道系统中的钢轨、轨道板、桥梁振动以及空间结构噪声开展系统对比测试研究,得到了很多重要结论。对于CRTS-Ⅱ型轨道系统,轨道板和桥梁之间用CA砂浆填充,而对于常规型CRTS-Ⅲ型轨道系统,轨道板和桥梁之间用自密实混凝土填充,其弹性模量较CA砂浆大很多,常规型CRTS-Ⅲ轨道系统弹性波反射系数较小,其下部结构振动问题比较突出。采用减振CRTS-Ⅲ型轨道系统的目的主要是通过在自密实混凝土和桥梁之间增设一个橡胶减振垫,降低轨道系统下部结构比如桥梁、地面等构件的振动,减少桥梁结构噪声和地面振动对沿线居民的影响。大量的仿真及现场测试研究证明,采用减振垫能够有效的降低桥梁结构振动。采用减振型轨道系统对下部结构有较多的研究,但针对车辆系统的振动影响研究不多,因此有必要进一步研究加设减振垫后车辆系统的动力性能。乘客的舒适性与车辆的振动直接相关,而评价舒适性的一个重要指标就是车辆的平稳性,减振CRTS-Ⅲ型轨道系统作为一种新型的轨道系统,研究在该系统上的车辆运行平稳性非常必要。对于车辆的平稳性,学者们开展了系列研究[6−10],大都是根据我国现有规范进行平稳性评价。现有的研究重点关注车辆参数的改变对平稳性的影响,Ha等[11]提出一种使用磁流变(MR)流体阻尼器来提高铁路车辆乘坐质量的半主动悬架系统,仿真结果表明,采用半主动控制MR阻尼器的铁路车辆车身的乘坐质量是可行的。 Berta等[12]评估铁路车辆悬架的弹性特性对车辆平稳性的影响。车身垂直刚度对车辆乘坐质量的影响,ZHOU等[13]建立包括车身柔性效应和所有垂直刚性模式的铁路客车垂直模型,利用模型和协方差方法对车体平稳性进行研究。Jason等[14]通过采用惰性装置的被动悬架来提高单级悬挂的双轴轨道车辆的乘坐质量的可能性。本文以减振CRTS-Ⅲ型轨道系统为研究对象,以常规CRTS-Ⅲ型轨道系统为参照,基于车辆、轨道和桥梁二维模型,利用动柔度法分别计算车辆和轨道(包含桥梁)的动柔度,建立频率域的车辆−轨道−桥梁耦合模型,计算车轮、转向架、车体以及钢轨、轨道板、桥梁的振动加速度并分析其规律。采用平稳性理论分析减振CRTS-Ⅲ型轨道系统下车辆的平 稳性。
1 轨道系统振动预测模型
以CRH3高速列车与客运专线高架箱梁为例,建立车辆−轨道−桥梁垂向耦合振动分析模型如图1所示。车辆考虑为10自由度的多刚体系统,钢轨、桥梁分别用无限长的Timoshenko梁和简支的Euler梁模拟,扣件系统和桥梁支座采用线性弹性阻尼单元模拟,轮轨接触关系采用线性化的Hertz弹性接触理论。
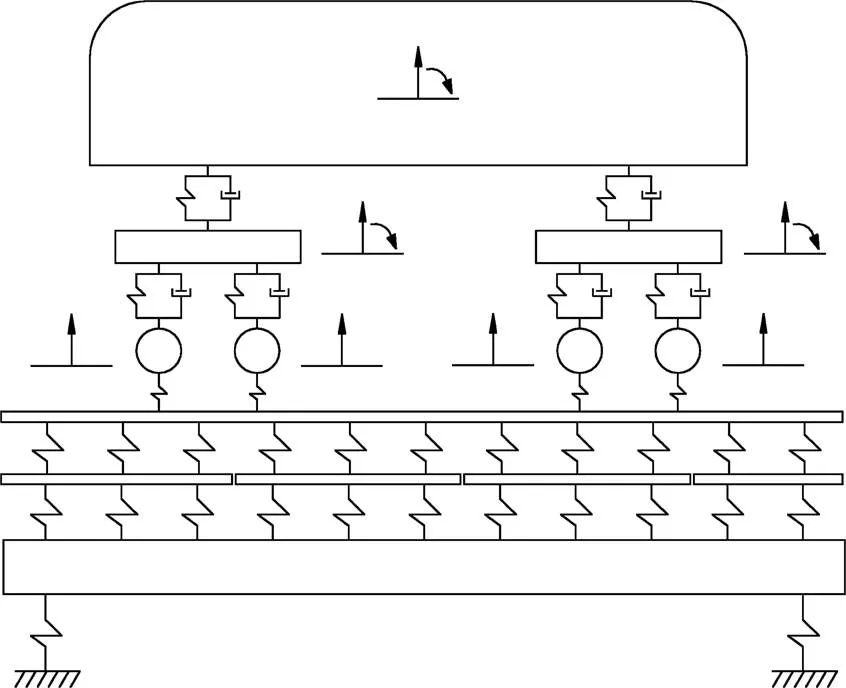
图1 车轨桥系统模型示意图
单节车辆模型的振动微分方程为
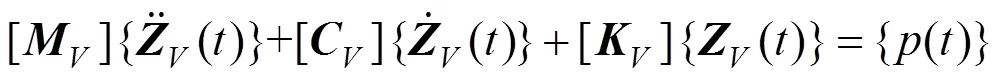
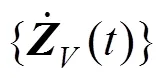
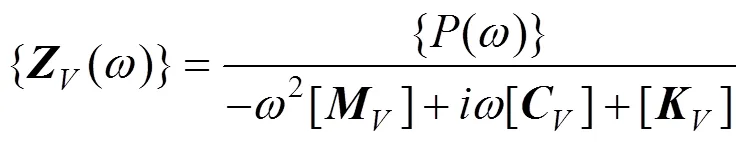
钢轨被视为无限长Timoshenko梁,其动柔度函数为
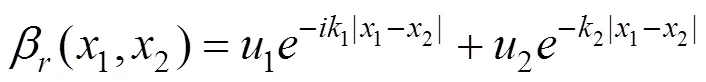
β(1,2)表示在钢轨上2处施加单位谐荷载在1处引起的位移。一跨桥梁上有若干个轨道板,其动柔度可以表示为
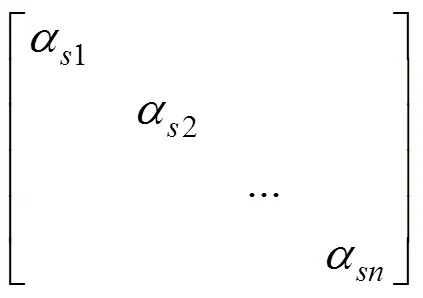
其中:1为一块轨道板的两端自由Euler梁动柔度,可采用模态叠加法计算,其动柔度可表示为
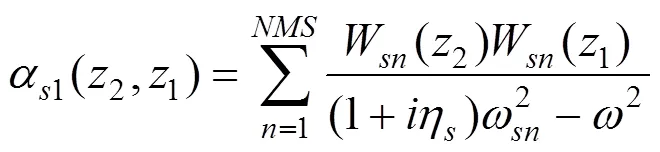
其中:W为Euler梁的第阶振型函数,则轨道板的运动方程可表示为
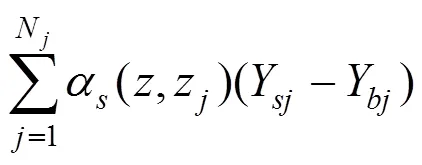
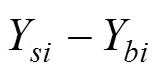
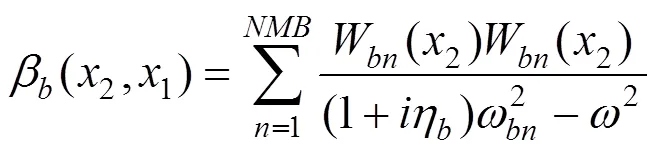
式中:W为简支梁的第阶振型函数;为简支梁第阶振型的固有频域;为简支梁的计算模态数;为激振的圆频率。利用动柔度的定义和叠加原理,箱梁在频域内的振动位移为
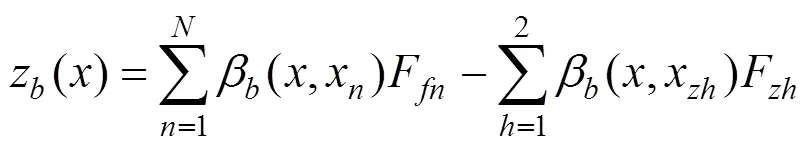
式中:F为第个桥梁支座施加到桥梁上x处的支座反力。综合式(3),(6)和(8)可以写成矩阵形式
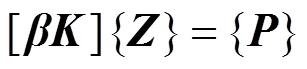
式中:[]主要由钢轨、轨道板、桥梁结构的动柔度乘以复刚度形成;[]由待求解的钢轨、轨道板、桥梁结构的位移组成;{}为荷载矩阵。
由于车轮模型轴距和定距的存在,不同轮轨接触点之间的激励出现时间滞后关系,图1模型中4个轮轨接触点的不平顺可表示为
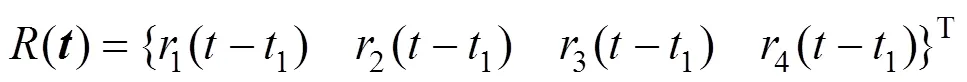
式中:假定1=0,则2=2l/,3=2l/,4=2(l+ l)/为车轮之间的时间差。其中,为车速,l和l分别为车轮轴距和定距之半。
假设时域的轨道不平顺为()=()e,则可得
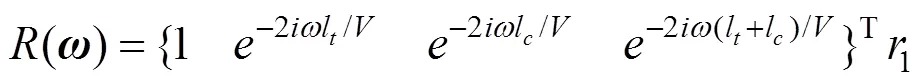
综合前述分析,利用频域轮轨相互作用模型并采用线性Hertz接触弹簧将车辆和轨道桥梁子系统进行耦合。以不平顺作为系统振动的激励源,假定车轮与轨道桥梁的相对位置不变,不平顺则以一定速度在车轮与钢轨之间移动,以此形成相对位移激励。则动态轮轨作用力可表示为
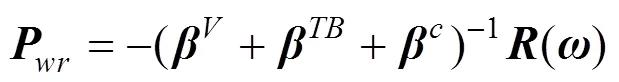
将求出的轮轨作用力代入式(2)和式(9),即可求出车辆系统、轨道系统结构频率域动力响应。
2 工程概况
2.1 轨道结构参数
选取高速铁路32 m双线预应力混凝土简支箱梁,桥梁标准跨径32 m,计算跨径31.5 m,桥梁中心线处梁高3.05 m,梁底宽5.5 m梁顶宽13.4 m。箱梁、轨道板采用C50混凝土。分别采用常规CRTS- Ⅲ型板式无砟轨道和减振CRTS-Ⅲ型板式无砟轨道模拟,其中常规CRTS-Ⅲ型板式无砟轨道系统从上往下结构依次为钢轨、轨道板、自密实混凝土、土工布、底座板和桥梁,而减振型CRTS-Ⅲ型板式无砟轨道系统从上往下依次为钢轨、轨道板、自密实混凝土、橡胶减振垫、底座板和桥梁,即采用在自密实混凝土和底座板之间增加一层橡胶减振垫。钢轨采用60 kg/m类型,扣件采用WJ-8型扣件系统。车辆以和谐号CRH3型动车为例,其参数如表1所示。轨道桥梁的结构参数如表2所示[15]。
2.2 车轮轨道不平顺
ISO3095:2005提供了具有较好平顺性的车轮轨道不平顺谱,其不平顺幅值主要与波长有关,用式(13)表示为[16]:
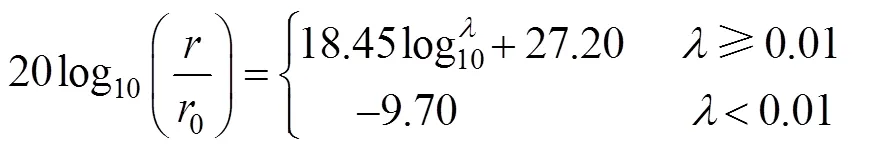

表1 CRH3型动车的计算参数
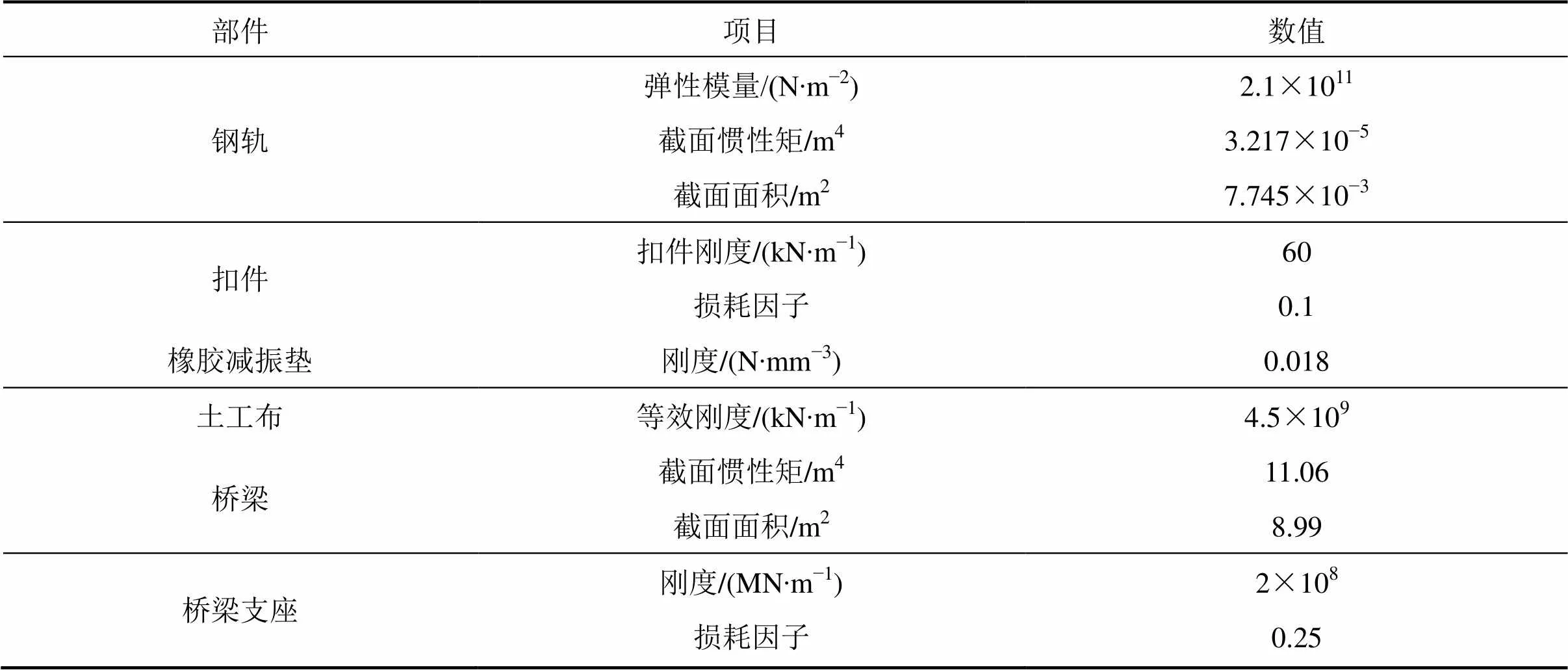
表2 轨道桥梁的计算参数
3 车辆轨道系统振动分析
3.1 轮轨力分析
轮轨力的大小和峰值频率对车辆系统和轨道系统的响应有直接关联,因此首先需分析研究频域轮轨力。利用上述公式采用MATALB编辑程序,其中车辆的运行速度为200 km/h,计算频域轮轨力。图2为常规型、减振型轨道系统下车轮1和车轮2的频域轮轨力曲线,其中轮1指远离跨中的车轮,轮2指靠近跨中的车轮。从图2可以看出,常规型轨道系统下车轮1和2的峰值频率分别为40 Hz和44 Hz,而减振型轨道系统的峰值频率分别为72 Hz和65 Hz。产生这一现象的原因是车辆−钢轨−轨道板−桥梁系统可以被假定为一个简单的质量−弹簧系统,轮轨力峰值频率对应系统共振频率。改变轨道系统的结构参数,也相应地改变了系统的共振频率,进而导致轮轨力的峰值频率发生偏移。在同一轨道系统条件下,车轮1和车轮2的轮轨力峰值差别不大。而在不同轨道系统下的轮轨力,减振型轨道系统较常规型CRTS-轨道系统轮轨力峰值分别降低23%和25%,采用减振垫后轮轨力有所降低。
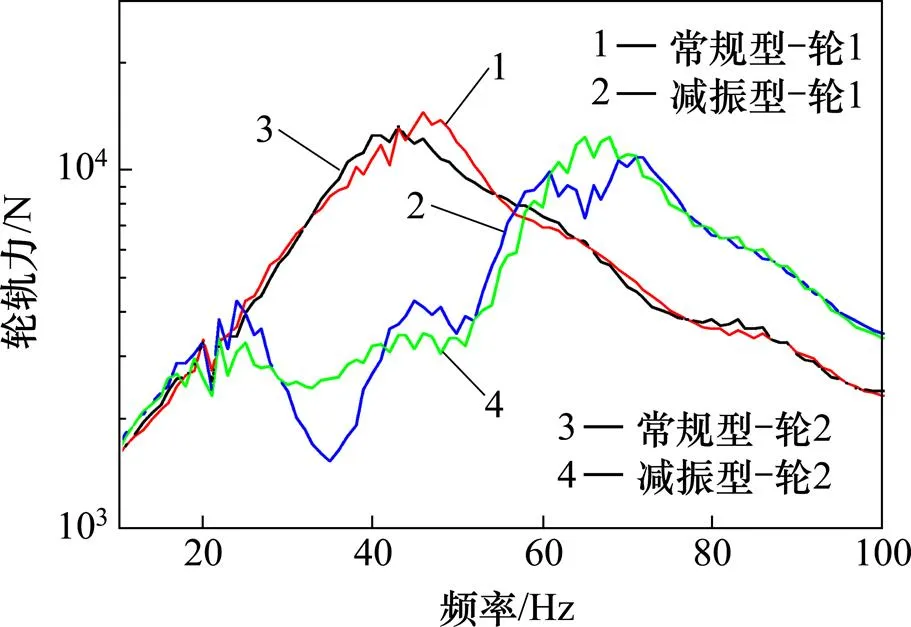
图2 频域轮轨力
3.2 轨道系统振动分析
选取钢轨、轨道板以及桥梁3个垂向振动加速度动力学指标进行分析。振动点选取三者跨中对应部位,计算结果见图3~5及表3所示。
1) 图3为常规型、减振型轨道系统条件下钢轨的频率−加速度曲线。从图中可以看出,常规型轨道系统条件下的峰值频率主要在44 Hz和85 Hz,而减振型轨道系统条件下钢轨的最大峰值频率为65 Hz,常规型轨道系统下45 Hz和减振型轨道系统下65Hz位置处的峰值由于轮轨力峰值频率导致。常规轨道系统加设减振垫后会削弱44 Hz和80 Hz位置处的加速度峰值,而在轮轨力峰值频率位置其加速度迅速变大,其加速度峰值约为常规型加速度峰值的1.69倍;
2) 轨道板的垂向振动加速度与钢轨具有相似的规律,常规型下轨道板在44 Hz和85 Hz位置处的峰值比较明显,减振型轨道板的振动加速度在65 Hz位置最大,在44 Hz和85 Hz位置处其加速度峰值有一定的削弱,减振型轨道板其最大加速度峰值为常规型轨道板的2.68倍,减振型的轨道板垂向振动加速度大大高于常规型的轨道板;
3) 由于常规型的混凝土与底座之间采用土工布隔离,而减振型是在自密实混凝土与底座之间采用橡胶垫隔离,橡胶具有较好隔离振动能量传递的特性。从图8可以看出,减振型轨道系统下桥梁在44 Hz和85 Hz位置处的加速度削减明显,但是在65Hz位置其加速度并没有放大,减振垫将65 Hz的轮轨力过滤,有效隔离了振动能量向桥梁构件传递。采用减振型轨道系统的桥梁的振动加速度峰值较常规型轨道系统条件下桥梁加速度峰值降低69.9%,加速度平均值降低60.4%,这与文献[1]中实测的桥面振动加速度平均值降低63.6%相近似。
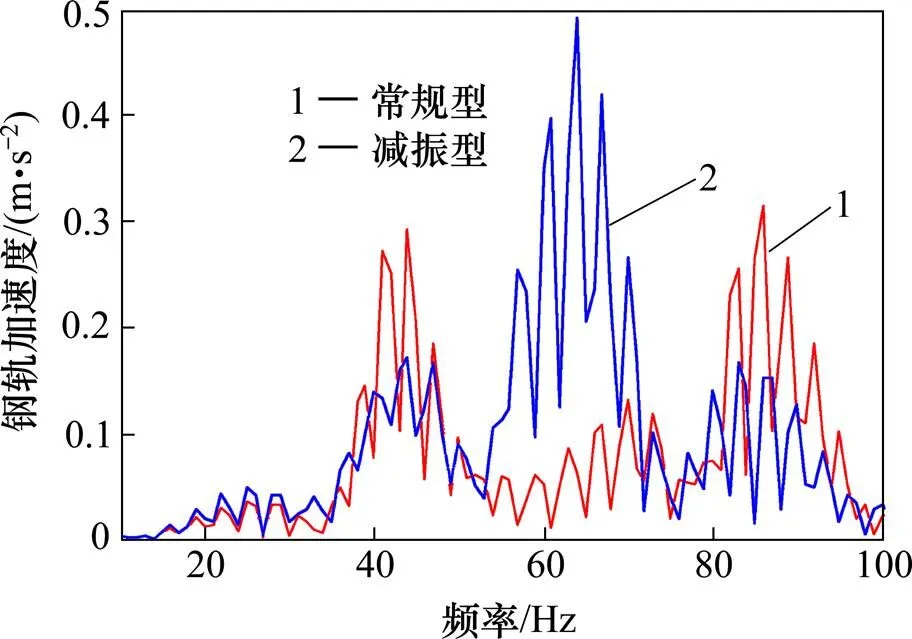
图3 钢轨垂向振动加速度
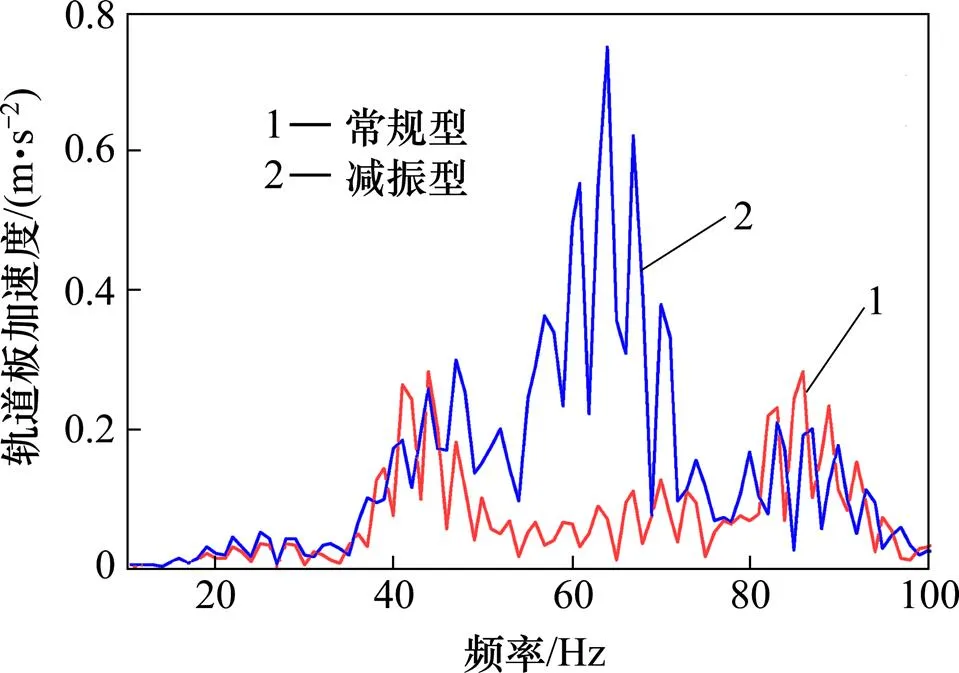
图4 轨道板垂向振动加速度
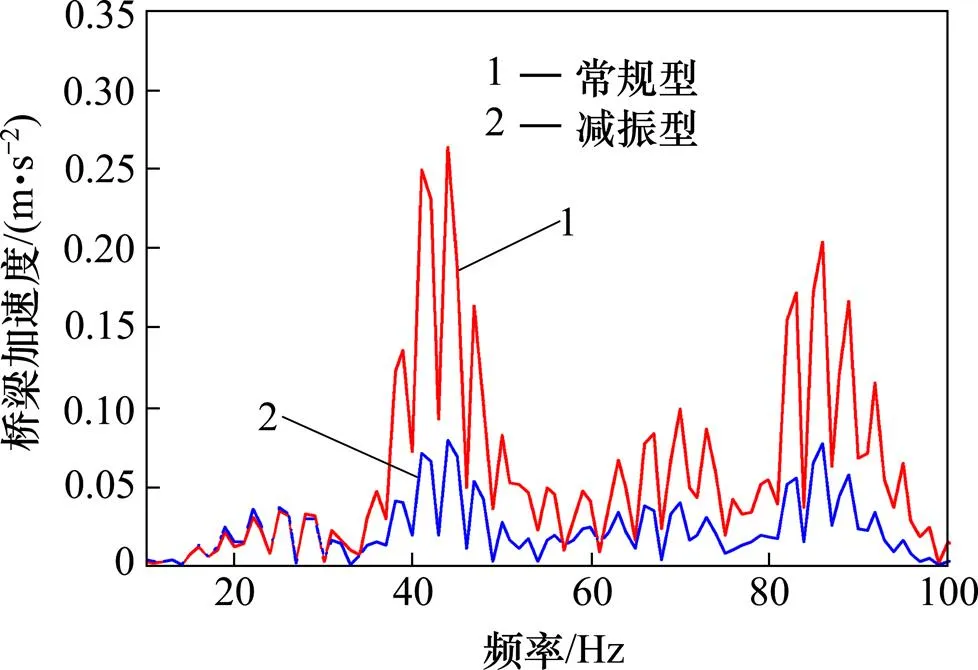
图5 桥梁垂向振动加速度
3.3 车辆系统振动分析
选取车轮、转向架、车体3个垂向振动加速度动力学指标进行分析。其中车轮取靠近跨中的车轮,计算结果见图6~8及表3所示。
1) 由于车轮直接承受轮轨力的作用,其加速度峰值频率与轮轨力峰值频率吻合较好,在43 Hz和65 Hz附近存在最大加速度。常规型轨道系统下轮轨力较减振型轨道系统下轮轨力更大,其对应的车轮加速度峰值分别为5.01 m/s2和4.32 m/s2,减振型轨道系统下车轮振动加速度降低13.6%。
2) 采用减振型轨道系统导致转向架峰值频率向高频方向偏移,其最大峰值频率由45 Hz偏移至65 Hz。常规型、减振型轨道条件下的转向架垂向加速度峰值分别为1.14 m/s2和0.54 m/s2,转向架垂向加速度降低52.6%,采用减振型轨道板能有效的降低转向架的垂向加速度。相对于车轮的加速度降低值,转向架的降低值远大于车轮,这是由于一系弹簧的隔离作用导致的。
3) 车体垂向加速度大小和对应的峰值频率直接关系到乘客的舒适性,从图8可以看出,常规型轨道板条件下的峰值频率主要集中在20 Hz和45 Hz,减振型轨道系统下轨道板的峰值频率在23 Hz,峰值频率向高频方向有轻微偏移。由于车体一系和二系弹簧的过滤作用,导致常规型轨道系统条件下车体在20 Hz和45 Hz其加速度峰值大小几乎相当,而减振型轨道系统条件下车体在23 Hz频率附近具有最大的加速度。
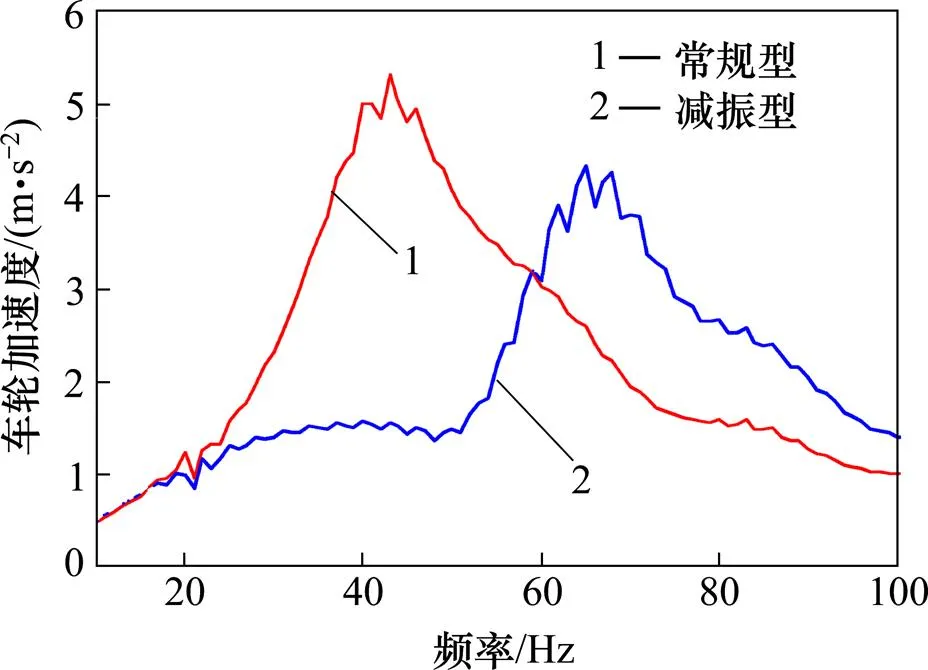
图6 车轮垂向振动加速度
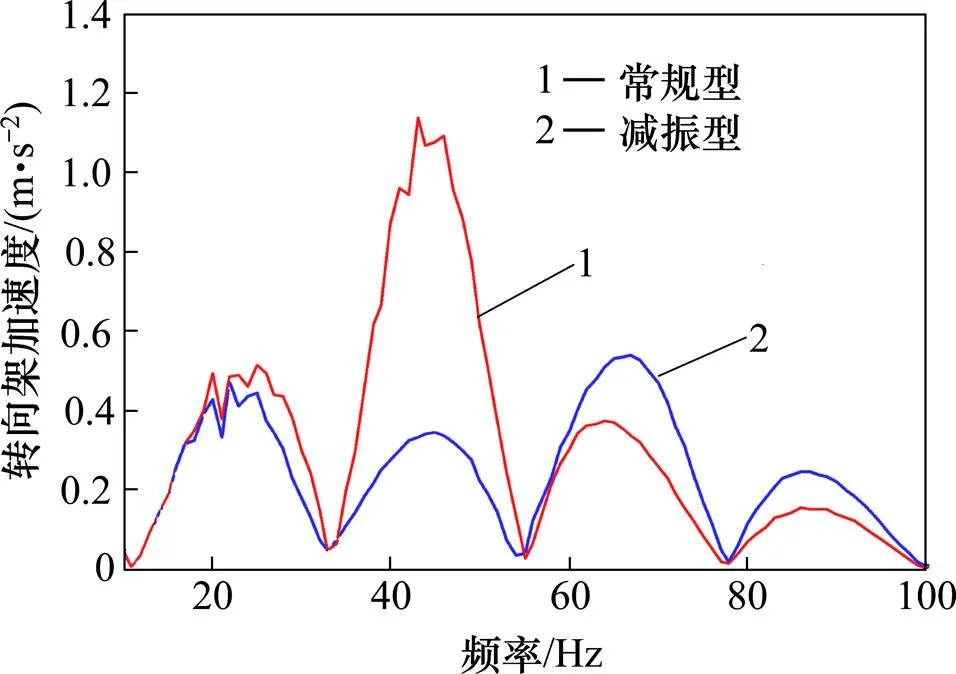
图7 转向架垂向振动加速度
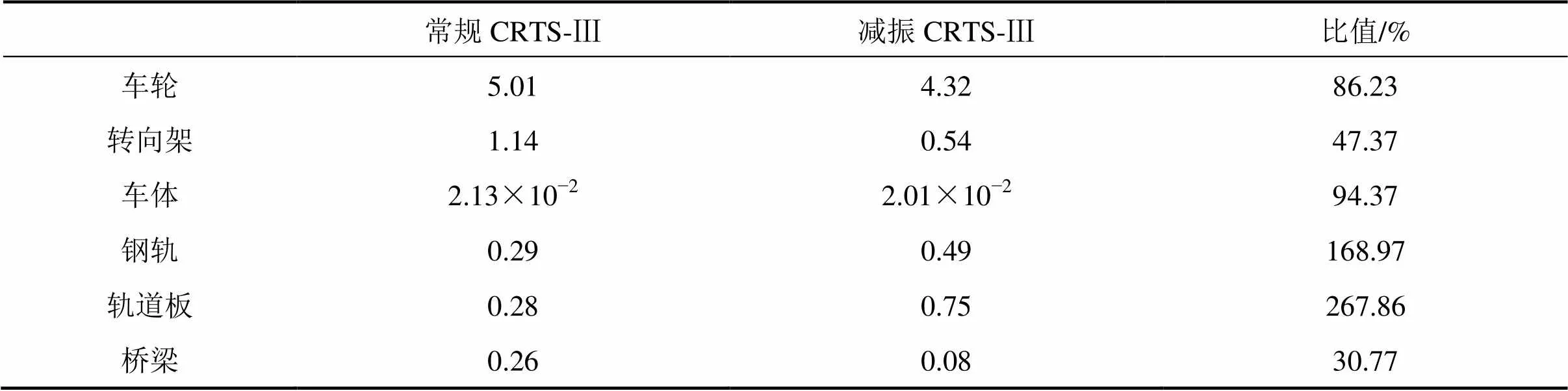
表3 不同轨道系统最大加速度
4 车辆平稳性评价
图8为1~100 Hz频域范围内车体加速度曲线,反映车体的加速度的瞬时幅值和频率关系,但是不能直接反映车体平稳性,因此有必要对车辆的平稳性进行研究。列车系统的平顺性指标是反映车体的振动性能和乘坐舒适性的综合指标。现有评价车辆平稳性的规范主要是《铁道车辆动力学性能评定和试验鉴定规范》(GB5599-85),由于本文只计算竖向振动,因此只对竖向平稳性进行评价,根据规范,客车运行平稳性指标按以下公式计算。
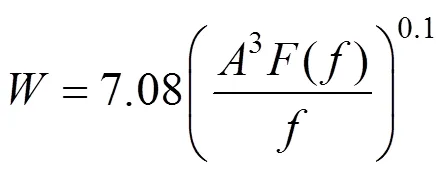
其中:为振动加速度;()为与振动频率相关的修正系数,其取值与频率范围有关如表4所示。
图8 车体垂向振动加速度
Fig. 8 Vertical vibration acceleration of vehicle body

表4 频率修正系数
平稳性指标适用于单一频率的等幅振动,而实际上车辆的振动幅值大小不一,车体的振动需要按频率分组,统计出每个频率中不同加速度的平稳性指标中。因此,总平稳性性指标采用下式计算[17],即
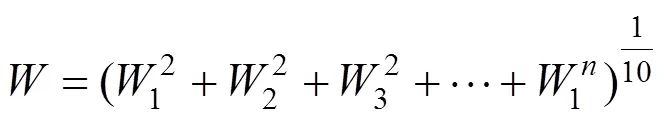
其中:1,2,…W为按频率分解进行频谱分析,根据每段频率范围内的加速度幅值计算得到的各自平稳性指标,经过频率加权得到车辆平稳性指标。根据计算得到的平稳性指标,采用表5对车辆的平稳性等级进行评判。

表5 平稳性评定
根据图8中得到的车辆振动加速度频率曲线,利用式(14)~(15)分别计算得到常规型和减振型轨道系统下车辆的平稳性值分别为2.70和2.61,根据表5的数值进行平稳性评定,2种轨道系统条件下车辆的平稳性为良好。减振轨道系统条件下的平稳性指标较常规型的平稳性指标降低4%,这与文献[5]中实测的竖向平稳性指标降低6%近似吻合,表明采用减振型轨道系统平稳性略有提高,乘客的舒适性也略有提高。结合图8分析,2种不同轨道系统条件下,车辆在1~20 Hz范围内振动加速度幅值变化不大,而在30~50 Hz范围内具有较大不同。从表4计算公式可以看出,频率修正系数随频率呈现先增大后减小的趋势,在5.9 Hz处频率修正系数最大,最大值达到11.31(11.49),而在20 Hz其频率修正系数迅速的降低为1,表明平稳性指标受车辆前20 Hz频率范围的振动幅值影响最大。从图8可以看出,在20 Hz范围内,不同轨道系统的车辆振动幅值变化不大,这也导致车辆的频平稳性变化较小,其值仅仅降低了4%,因此,在改变轨道系统对人的舒适度方面略有提高。
5 结论
1) 采用橡胶减振垫刚度为0.018 N/m3的减振轨道系统,钢轨和轨道板的振动加速度峰值增大2.6和1.3倍,桥梁的振动峰值加速度降低69.9%。采用减振轨道系统增大了减振垫上层的钢轨和轨道板的振动加速度,降低了减振垫下层的桥梁的振动加速度。
2) 采用橡胶减振垫刚度为0.018 N/m3的减振轨道系统,车轮和转向架的振动加速度峰值较常规型分别降低13.6%和52.6%。车体在1~20 Hz范围内振动加速度幅值变化不大,35~50 Hz范围内降低明显。
3) 2种轨道系统条件下的车辆竖向平稳性指标分别为2.70和2.61。减振型轨道系统条件下的竖向平稳性指标较常规型的平稳性指标降低4%,乘客的舒适性略有提高。
本文仿真模型仅仅考虑竖向振动,未考虑车辆的横向振动,因此不能对车辆横向的平稳性进行分析。由于乘客的舒适性不光取决于竖向振动,横向振动也是一个重要的评价指标。下一步将进一步完善车辆轨道耦合模型,使减振CRTIS-Ⅲ轨道系统下车体的平稳性得到更准确的判断。
[1] 赵才友, 王平. 桥上无作轨道橡胶减振垫减振性能试验研究[J]. 中国铁道科学, 2013, 34(4): 8−13. ZHAO Caiyou, WANG Ping. Experimental study on the vibration damping rubber absorbers for ballastless tracks performance of on viaduct[J]. China Railway Science, 2013, 34(4): 8−13.
[2] 辛涛, 张琦, 高亮, 等. 高速铁路CRTS Ⅲ型板式无砟轨道减振垫层动力影响及结构优化[J]. 中国铁道科学, 2016, 37(5): 1−7. XIN Tao, ZHANG Qi, GAO Liang, et al. Dynamic effects and structure optimization of damping layers of CRTS Ⅲ slab ballastless track for high speed railway[J]. China Railway Science, 2016, 37(5): 1−7.
[3] 任娟娟, 赵华卫, 李潇, 等. 减振CRTS Ⅲ型板式无砟轨道结构谐响应分析[J]. 铁道工程学报, 2016, 210(3): 44−50. REN Juanjuan, ZHAO Huawei, LI Xiao, et al. Analysis of harmonic response of CRTS III prefabricated slab track with anti-vibration structure[J]. Journal of Railway Engineering Society, 2016, 210(3): 44−50.
[4] 周毅. CRTS Ⅲ型板式轨道减振特性研究[D]. 成都: 西南交通大学, 2011. ZHOU Yi. Research on vibration-reduction performance of CRTSⅢ slab ballastless track[D]. Chengdu: Southwest Jiaotong University, 2011.
[5] ZHAO Caiyou, WANG Ping. Effect of elastic rubber mats on the reduction of vibration and noise in high-speed elevated railway systems[J]. Proc ImechE Part F: J Rail and Rapid Transit, 2018, 32(1): 1−15.
[6] 刘宏友, 曾京. 列车系统运行平稳性研究[J]. 中国铁道科学, 20 04, 25(5): 22−27. LIU Hongyou, ZENG Jing. Study on ride comfort of train system[J]. China Railway Science, 2004, 25(5): 22−27.
[7] 向俊, 曾庆元. 京通线烟囱沟桥上列车走行安全性、舒适性及平稳性分析[J]. 土木工程学报, 2005(7): 65−70.XIANG Jun, ZENG Qingyuan. Safety, comfort and smoothness analyses of trains running on The Yanconggou Bridge in the Jingtiong rail road[J]. China Civil Engineering Journal, 2005(7): 65−70.
[8] 罗仁, 曾京, 戴焕云. 列车系统建模及运行平稳性分析[J]. 中国铁道科学, 2006, 27(1): 72−77. LUO Ren, ZENG Jing, DAI Huanyun. Modeling and ride quality analysis of railway train system[J]. China Railway Science, 2006, 27(1): 72−77.
[9] 张小华, 孙德华, 张晚晴, 等. QY-2型减振扣件对列车运行平稳性影响的测试与分析[J]. 噪声与振动控制, 2017, 37(1): 86−88. ZHANG Xiaohua, SUN Dehua, ZHANG Wanqing, et al. Measurement and analysis of the influence of QY-2 damper fastener on train running stability[J]. Noise and Vibration Control, 2017, 37(1): 86−88.
[10] 马思群, 王猛, 王晓杰, 等. 高速列车平稳性与乘坐舒适度测试及评价[J]. 大连交通大学学报, 2015, 36(增1): 66−68. MA Siqun, WANG Meng, WANG Xiaojie, et al. Evaluation and measurement of high speed train by ride comfort and ride index[J]. Journal of Dalian Jiaotong University, 2015, 36(Suppl 1): 66−68.
[11] Ha Sung Hoon, Choi J Seung-Bok, Lee Kyu-Seob, et al. Ride quality evaluation of railway vehicle suspension system featured by magnetorheological fluid damper[J]. Advanced Science Letters, 2012, 12(1): 209−213.
[12] Berta Suarez, Jose Manuel Mera,Maria Luisa Martinez, et al. Assessment of the influence of the elastic properties of rail vehicle suspensions on safety, ride quality and track fatigue[J]. Vehicle System Dynamics, 2013, 51(2): 280−300.
[13] ZHOU J, Goodall R, REN L, et al. Influences of car body vertical flexibility on ride quality of passenger railway vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2014, 223(5): 461−471.
[14] Jason Zheng Jiang, Alejandra Z, Matamoros Sanchez, et al. Passive suspensions for ride quality improvement of two-axle railway vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2013, 229(3): 315−329.
[15] 石广田, 杨建近, 杨新文, 等. 基于动柔度法的车-线-桥垂向耦合振动分析[J]. 中南大学学报(自然科学版), 2017, 48(4): 1119−1126. SHI Guantian, YANG Jianjin, YANG Xinwen, et al. Vertical vehicle-track-bridge coupling vibration based on dynamic flexibility method[J]. Journal of Central South University (Science and Technology), 2017, 48(4): 1119− 1126.
[16] ZHANG Xun, LI Xiaozhen, HAO Hong, et al. A case study of interior low-frequency noise from box-shaped bridge girders induced by running trains: Its mechanism, prediction and countermeasures[J]. Journal of Sound and Vibration, 2016, 367: 129−144.
[17] 雷晓燕. 高速铁路轨道动力学−模型、算法与应用[M].北京: 科学出版社, 2015: 229. LEI Xiaoyan. High speed railway track dynamics: model, algorithm and application[M]. Beijing: Sicence Press, 2015: 229.
Vibration and ride quality analysis of CRTS-III ballastless track with anti-vibration structure on railway bridge
SONG Rui1, 2, LIU Linya2, XU Bing1, ZENG Kaihua1
(1. College of Civil Engineering and Architecture, Nanchang Institute of Technology, Nanchang 330029, China; 2. Engineering Research Center of Railway Environment Vibration and Noise Ministry of Education, East China Jiaotong University, Nanchang 330013, China)
In order to study the vibration effect of the vibration attenuation CRTS- III ballastless track system on the car body system and the track system, and to analyze the vehicle stability index, based on the two dimensional model of vehicle and track system, the dynamic flexibility of vehicle and track system was calculated by the dynamic flexibility method, and the vehicle and track coupling model of the frequency domain was established, and the vehicle and the rail were calculated. Vibration acceleration of the track system was analyzed, and its ride quality was calculated. The results show that compared with the conventional CRTS-III type track, the peak wheel-rail force of the damping rail system with the vibration-absorbing pad stiffness of 0.018 N/m3is reduced, and the vibration acceleration of the wheel and bogie is reduced by 13.6% and 52.6% respectively. The vibration of the car body in the 1~20 Hz range is not significant; the vibration acceleration of rails and track plates increases by 1.69 and 2.68 times, the vibration acceleration of the bridge decreases by 69.9%; the ride comfort indexes of vehicles are 2.70 and 2.61, respectively. The stability index decreases by 4%. Comparing with the conventional CRTS-III ballastless track system, the vibration acceleration of each subsystem of the vehicle is reduced in varying degrees under the condition of vibration damping CRTS-III ballastless track system. Vibration acceleration of rail and track increases and the vibration acceleration of the bridge decreases. The ride quality index of vehicles is reduced, and the comfort of passengers is improved to a certain extent.
railway bridge; vibration attenuation CRTS- III type track system; vibration; ride quality
10.19713/j.cnki.43−1423/u.2019.04.001
U213.2+44
A
1672 − 7029(2019)04 − 0835 − 08
2018−05−16
江西省教育厅科技项目(GJJ170984);国家自然科学基金资助项目(51578238,51569016,51769016)
刘林芽(1973−),男,江西樟树人,教授,博士,从事铁路环境振动与噪声研究;E−mail:lly1949@163.com
(编辑 阳丽霞)
