有轨电车嵌入式轨道路基结构动应力分布规律
2019-04-26冯青松孙魁雷晓燕罗锟刘庆杰
冯青松,孙魁,雷晓燕,罗锟,刘庆杰
有轨电车嵌入式轨道路基结构动应力分布规律
冯青松,孙魁,雷晓燕,罗锟,刘庆杰
(华东交通大学 铁路环境振动与噪声教育部工程研究中心,江西 南昌 330013)
为分析列车荷载作用下有轨电车嵌入式轨道路基结构动应力分布规律,建立现代有轨电车车辆动力学模型和三维精细化的非线性轨道-路基-地基动力学计算模型,获得在不平顺谱激励下的动态轮轨垂向力,研究列车荷载作用下嵌入式轨道路基结构中动应力沿横向、垂向和纵向的分布规律。研究结果表明:在移动列车荷载作用下,轨道路基结构中的动应力沿横向都呈现驼峰形,且应力极值均出现在钢轨下方;同时在距轨道中心线约1.5 m处,基床表层竖向动应力约等于0,表明路基面宽度取为4 m是合理的;当取自重应力的20%作为参考标准时,列车荷载在路基中的影响深度为0.75 m;当列车速度为70 km/h时,路基基床表层动应力纵向影响范围约为8.8 m;在对轨道结构进行设计时,建议采用单轴双轮加载,而对路基结构进行设计时,建议使用双轴四轮进行加载。
有轨电车;嵌入式轨道;动应力;分布规律;影响深度
与传统公交相比,现代有轨电车具有运量大、美观、环保和节能等特点,能够在很大程度上缓解城市交通拥堵问题,因此其逐渐成为一种新型的城市轨道交通方式[1−2]。国内外学者针对轨道路基结构中动应力分布情况开展了大量的研究。薛富春等[3]以高速铁路为研究对象,采用有限元软件Abaqus建立精细化三维轨道−路基−地基有限元模型,研究了轨道和路基结构中动应力沿纵向、横向和深度方向的分布情况;宋小林等[4]采用Ansys软件建立CRTSⅡ型板式无砟轨道路基计算模型,分析了不同速度的移动荷载作用下轨道和路基中动应力沿横向和深度的分布规律;肖世伟等[5]采用FLAC3D软件建立重载铁路有砟轨道路基有限元分析模型,研究了道砟和路基的结构参数对路基动力响应的影响;Costa等[6]在考虑土体非线性的基础之上,研究了路基结构的动应力特性和临界速度;CAI等[7−8]采用Boit理论模拟下部路基结构,研究了列车荷载作用下路基动应力分布规律;BIAN等[9]采用实尺模型试验的方法,研究了列车荷载作用下轨道和路基结构的振动和动应力特性,并基于试验数据提出了路基动应力估算公式。综上所述,轨道路基动应力问题一直受到广大学者的关注。但嵌入式轨道结构采用高分子复合材料取代了传统扣件,即钢轨由离散点支承变为了连续支承,这可能将会对轨道和路基中的动应力分布规律产生一定的影响。同时,由于现代有轨电车兴起时间仍较短,在轨道路基结构设计过程中,常常参考高铁和地铁设计规范,但有轨电车车辆型式、轴重和运行速度都与高铁和地铁有较大的区别,且关于有轨电车轨道路基中动应力的研究较少,因此,十分有必要对有轨电车嵌入式轨道路基中的动应力分布规律进行研究。本文分别采用多体动力学软件Simpack和大型通用有限元软件Ansys建立有轨电车车辆模型和嵌入式轨道路基地基三维精细化模型,将通过车辆模型获取的动态轮轨垂向力施加在轨道路基地基模型上,研究列车动荷载作用下有轨电车轨道路基结构中的动应力分布规律。
1 数值分析模型
1.1 计算模型与参数
现代有轨电车嵌入式无砟轨道路基结构主要由60R2槽型轨、高分子填充材料、道床板、素混凝土支承层和下部路基组成,如图1所示。
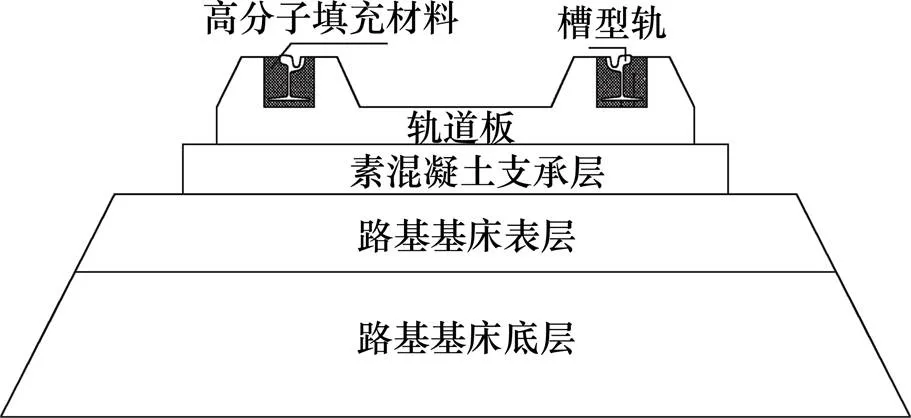
图1 有轨电车嵌入式轨道路基结构
承轨槽中的聚氨酯高分子填充材料是一种高度非线性材料,其真实本构关系很难正确模拟,同时考虑到高分子填充材料主要起到传递荷载的作用,因此本文将其本构简化为线弹性本构关系,采用SOLID45实体单元模拟。根据本文所依托实际工程,高分子填充材料的弹性模量取为5 MPa。
钢轨、轨道板和素混凝土支承层均采用SOLID45实体单元模拟,具体计算参数如表1所示。

表1 轨道结构计算参数
路基基床表层和底层采用Drucker-Prager理想弹塑性本构模型进行模拟,其弹性模量根据压实指标K30换算而来,泊松比统一取为0.3。路基面宽度为4 m,基床表层厚度0.4 m,黏聚力为32 kPa,内摩擦角为75°,基床底层厚度为0.6 m,黏聚力为26 kPa,内摩擦角为25°。
为了消除由于模型的边界效应所带来的计算误差,建立5 m×6 m长的有限元模型,以中间一块轨道板长度范围内的轨道路基结构为研究对象,分析有轨电车嵌入式无砟轨道结构中动应力分布规律。由于路基下部的地基对于整个轨道路基结构的受力和变形都有较大的影响,因此,在模型中考虑了地基。图2即为建立的有轨电车嵌入式无砟轨道−路基系统有限元模型。
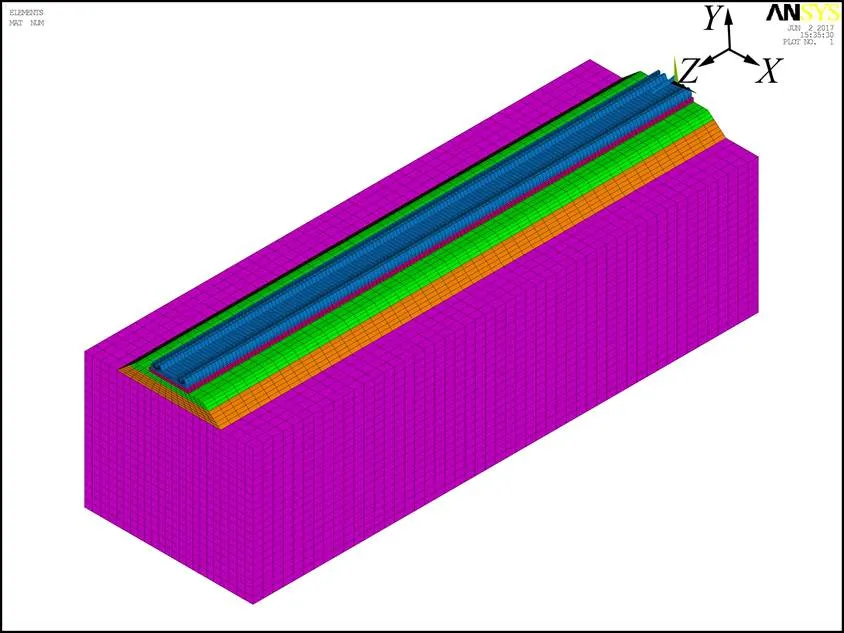
图2 有轨电车无砟轨道-路基系统有限元模型
1.2 车辆模型
广州市海珠环岛有轨电车车辆为世界首列超级电容100%低地板有轨电车,车辆长度约36 m,最大载客量为368人,最高运行速度为70 km/h。
全车由4个模块组成,其中2节车为1组,整列车共2组,每节车体的中部正下方都设有转向架。车体与车体间通过铰接装置使4节车的地板面贯通。现代低地板有轨电车单节车辆模型之间通过6个铰接实现整车模型的建立,每节车辆之间上、下铰接各1个,并全部设置在车体间的中间位置,上部铰接为转动铰,下部铰接为固定铰,如图3所示。
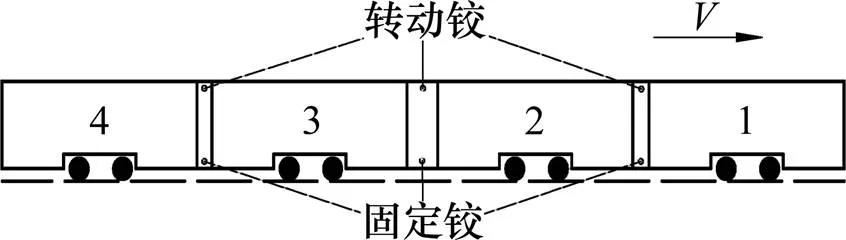
图3 列车编组和铰接方式示意图
为了正确模拟有轨电车车轮与槽型钢轨之间相互作用关系,分别根据槽型钢轨和车轮的实际几何尺寸定义钢轨型面车轮踏面文件。同时,轮轨垂向力通过赫兹接触理论进行计算。整车共有80个自由度,车辆动力学模型如图4所示。车辆模型参数如表2所示。
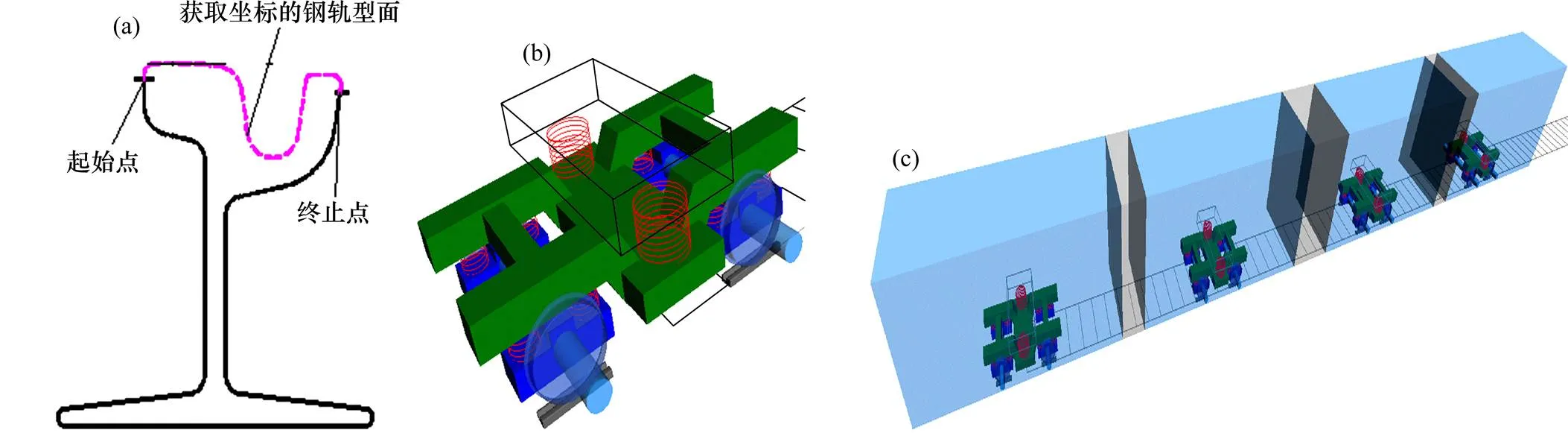
(a) 槽型钢轨型面;(b) 转向架模型;(c) 整车模型
鉴于国内暂无城市轨道交通不平顺谱的相关规定,因此本文选择美国5级不平顺谱作为输入激励。同时由于本文主要研究有轨电车嵌入式轨道路基结构在垂向荷载作用下的应力分布规律,这里仅列出轨道高低不平顺功率谱密度计算公式,如式(1)所示。
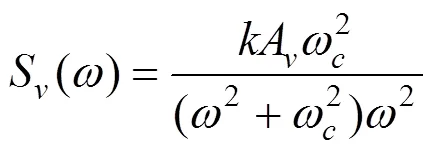
式中:S()为轨道不平顺功率谱密度,cm2/(rad∙m);为空间频率,rad/m;为截断频率,rad/m,取为0.824 5;A为粗糙度系数,cm2/(rad∙m),取为0.209 5;一般取0.25。
通过Simpack仿真分析,计算得到速度为70 km/h时的有轨电车动态轮轨力,同样只提取轮轨垂向作用力时程,如图5所示。
表2 有轨电车车辆模型参数
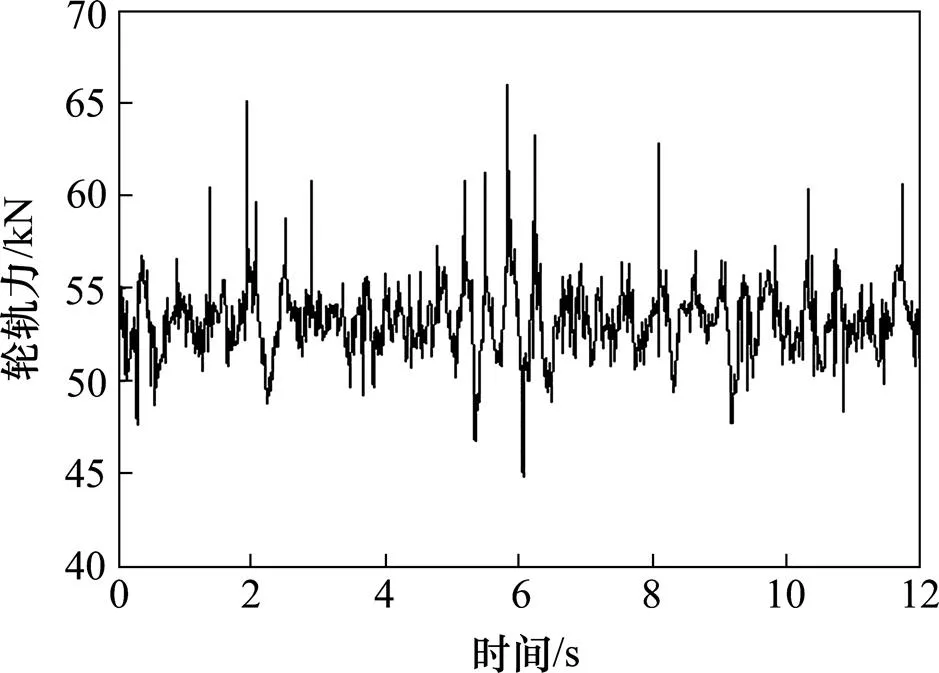
图5 轮轨垂向力时程曲线
1.3 边界条件
用有限域来模拟地基的无限域,势必会在边界处发生应力波的透射和反射,为避免边界处应力波的反射对计算结果的影响,采用一致黏弹性人工边界[10]。
在地基底面施加固定边界条件,同时约束其4个侧面的水平向位移,路基各侧面不施加约束。
2 计算结果与分析
2.1 竖向动应力沿横向的分布规律
图6为轨道板、支承层、基床表层和基床底层的底部竖向动应力横向分布规律曲线。
从图6可以看出,在列车荷载作用下,不同结构层的竖向应力幅值均位于钢轨正下方的位置,在2股钢轨之间,应力水平基本保持一致,轨道板、支承层、基床表层和基床底层竖向应力的横向分布曲线呈驼峰形。
从图6(a)可以看出,由于列车荷载直接作用在槽型钢轨上,从而使得钢轨产生较大的弯曲变形,轨道板也相应地产生较大的变形,故在钢轨正下方轨道板的竖向应力达到最大值,为121.5 kPa。而轨道板中间部分由于没有直接承受列车荷载且距离荷载较远,故竖向应力几乎为0。
同时,从图6(b)中可以发现,素混凝土支承的竖向应力的分布规律基本与轨道板相同,其竖向应力最大值依然位于钢轨正下方,为39.2 kPa。在距轨道中心线两侧0.5 m范围内,支承层竖向应力水平保持一致,约为钢轨正下方处竖向应力值的66.7%。在距轨道中心线0.5~0.72 m范围内,支承层竖向应力逐渐增至最大值。随距轨道中心线距离的进一步增加,支承层的竖向应力又逐渐减小,这主要是由于距离荷载的横向距离逐渐增大和支承层上方的轨道在荷载作用下发生翘曲变形造成的。
对比分析图6(c)和6(d)可知,列车荷载在嵌入轨道路基结构中所产生的动应力在经过轨道板和素混凝土支承层的扩散和衰减作用之后,到达路基基床结构的动应力已经得到了很大程度的衰减,故基床结构的动应力横向分布较轨道板和支承层要更加均匀。基床表层和底层的竖向应力幅值依然位于钢轨正下方,分别为8.1 kPa和3.2 kPa,基床底层相对于基床表层而言其竖向应力幅值减少了60.4%。同时可以发现,在距轨道中心线约1.5 m处,基床表层竖向动应力约等于0,说明路基面宽度取为4 m是合理的。
综上所述,随着距荷载作用点的垂向距离的增加,轨道路基结构各层的竖向应力均逐渐减小,横向分布情况也越均匀。与文献[3]中计算结果对比可知,钢轨支承方式的改变对轨道路基中的垂向动应力分布规律影响较小。
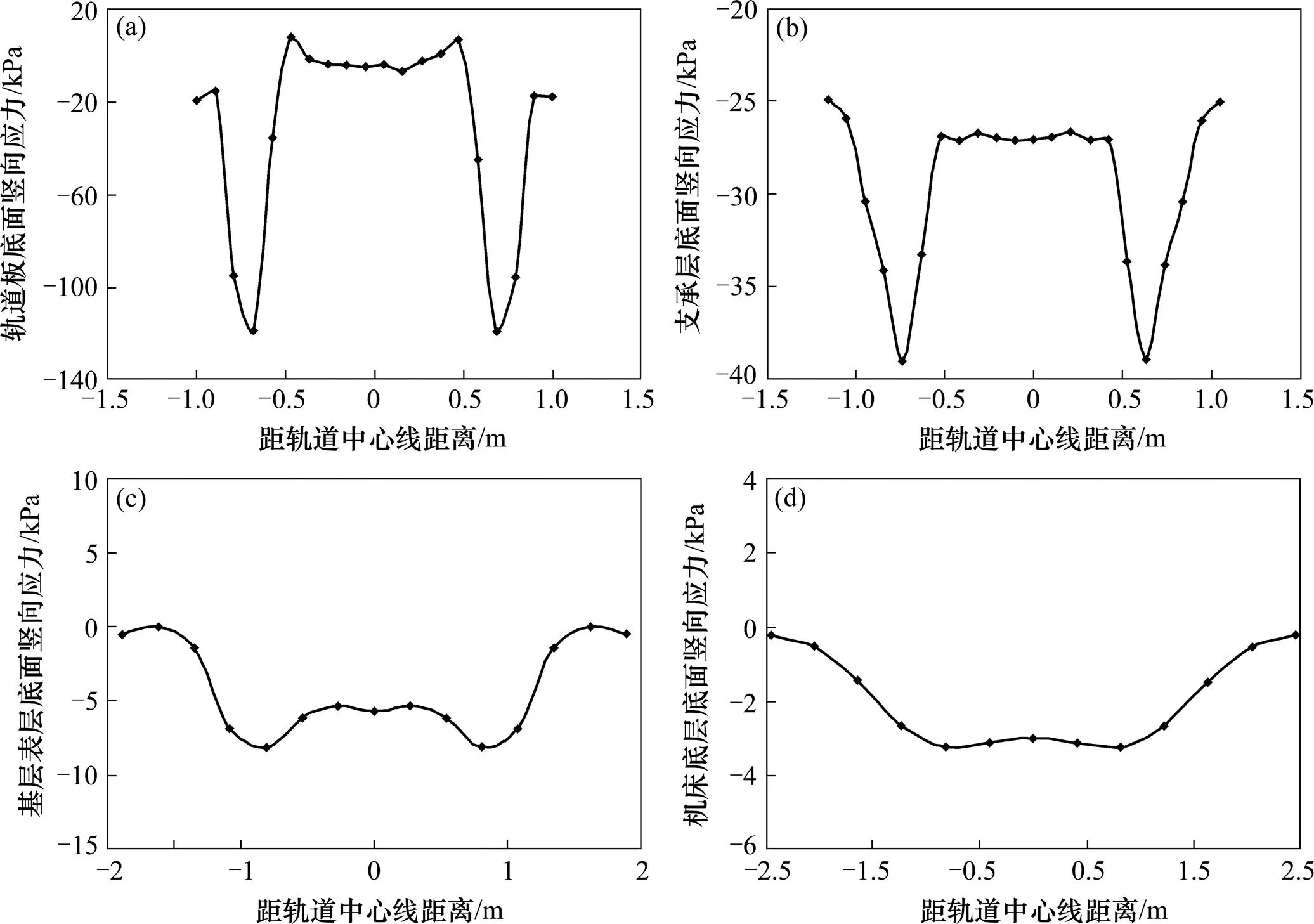
(a) 轨道板底面;(b) 支承层底面;(c) 基床表层底面;(d) 基床底层底面
2.2 路基动应力沿深度的分布规律
路基基床的结构分基床表层和基床底层这2个部分,对于列车的安全正常运营有着十分重要的影响。基床总厚度通常是通过列车动应力的影响深度来确定的,国内Ⅱ级以上铁路一般依据列车荷载产生的动应力是路基自重应力的20%或10%来确定基床厚度。考虑到新型有轨电车的轴重一般不大于12.5 t,路基基床填料较好,且压实度要求高,因此采用动应力与自重应力之比20%为确定基床厚度的标准。为了消除边界效应的影响,当导向轮对所对应的轮轨力运行到模型中部时,提取模型中部路基基床不同深度处的动应力,同时假设轨道结构和路基的平均容重为20 kN/m3,则基床中的动应力沿深度的衰减规律如图7所示。
根据实测结果,当有轨电车速度为60 km/h时,路基顶面最大动应力为10.5 kPa[11]。从图7可以看出,路基基床表面的最大动应力为13.2 kPa,本文计算结果偏大的主要原因是本文列车运行速度为70 km/h且采用轨道结构形式差异较大,因此可以验证本文计算结果的可靠性。
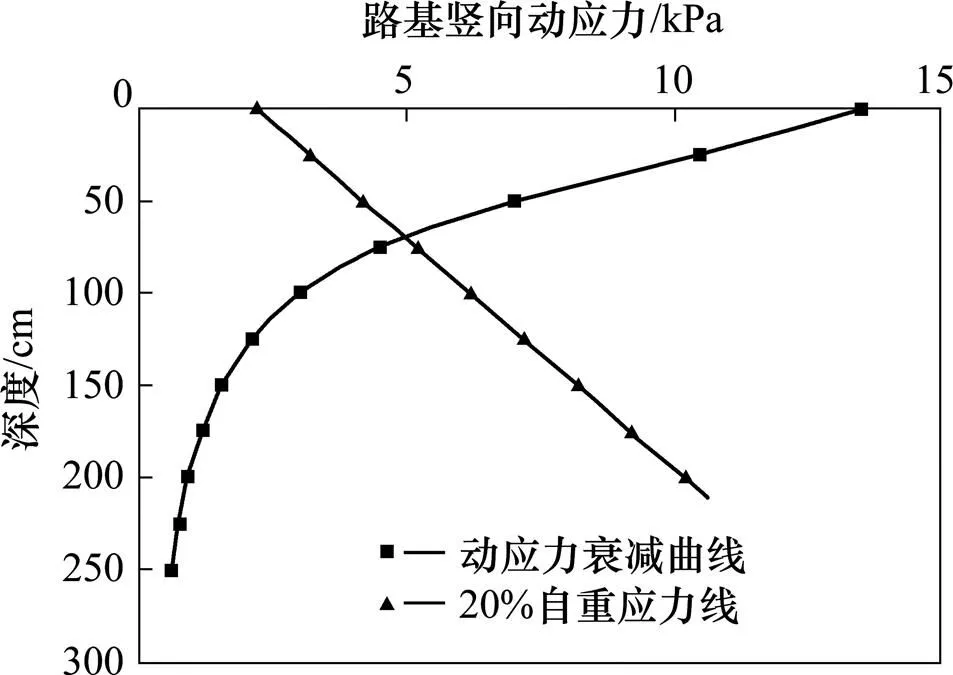
图7 路基竖向动应力深度分布曲线
列车荷载所产生的应力波在传播的过程中,由于阻尼作用路基土体要吸收能量,因此动应力随着路基深度的增加而逐渐减小。在基床表层范围内(0~0.4 m),路基竖向动应力快速衰减,当动应力传递到基床表层底部时,最大动应力仅为8.1 kPa,约为基床表层表面动应力的61.3%。在基床底层范围内(0.4~1.0 m),路基竖向动应力衰减速度较慢,基床底层底面的动应力值为3.2 kPa,约为基床底层表面动应力的41.3%。同时,从图中可以发现,本文计算所得路基竖向应力衰减曲线与20%自重应力曲线相交于距基床表层表面约为0.75 m处,即有轨电车的列车荷载影响深度约为距基床表层表面0.75 m。
2.3 竖向动应力沿纵向的影响范围
轨道板表面、支承层表面和路基基床表层表面的竖向动应力时程曲线如图8所示。
图8(a)为轨道板表面竖向动应力时程曲线,该曲线较好地反映了4节编组的有轨电车运行过程,且该曲线具有8个应力峰值,正好与有轨电车车辆的轮对数相同,说明嵌入式无砟轨道的轨道板所承受的竖向动应力的一次加载卸载过程由单个轮对作用完成。
图8(b)为支承层表面竖向动应力时程曲线,从该曲线中同样可以清晰地辨别出4节编组的有轨电车的走形痕迹。同时该曲线也具有8个应力峰值,说明支承层所承受的竖向动应力的一次加载卸载过程和轨道板相同。
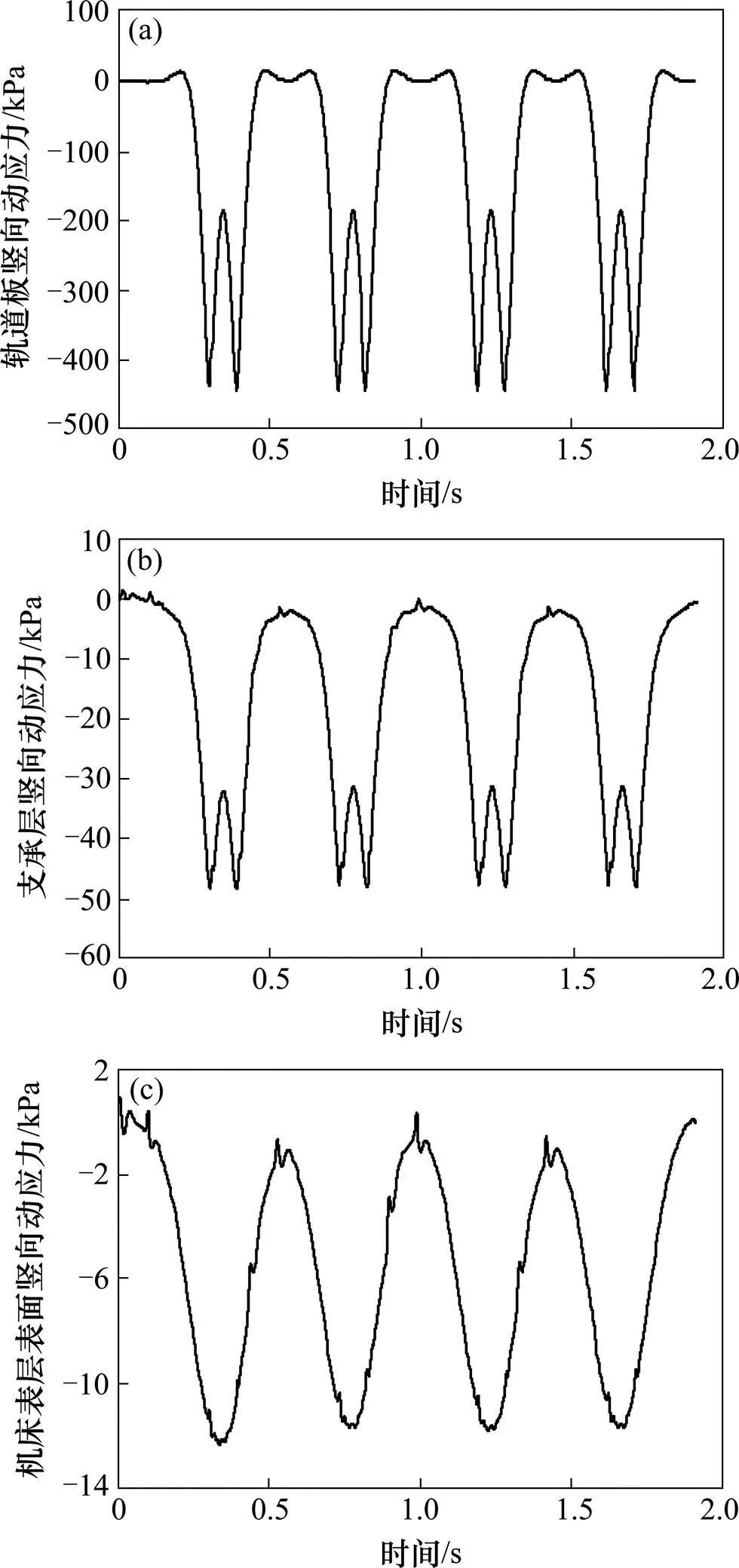
(a) 轨道板表面竖向动应力时程曲线;(b) 支承层表面竖向动应力时程曲线;(c) 基床表层表面竖向动应力时程曲线
图8(c)为路基基床表层表面的竖向动应力时程曲线,该曲线具有4个应力峰值,正好与有轨电车车辆的转向架个数相同,即该曲线已经不能够分辨出轮对的走形痕迹,同时也说明路基基床表层表面所承受的竖向动应力的一次加载卸载过程由1个转向架的2个轮对共同作用完成。
通过上述分析,可以将轨道板、支承层和路基基床表层的竖向动应力曲线分为2类:1) 第1类为在1个应力的加载卸载过程中,完全由单个轮对作用完成,如轨道板和支承层竖向应力曲线;2) 第2类为在1个完整的应力加载卸载过程中,由1个转向架的2个轮对共同作用完成,即出现叠加现象,如路基基床表层竖向应力曲线。
对于第2类曲线,当转向架的前轮对距测点距离为时,传感器开始记录荷载,当转向架的后轮对远离测点距离为时,由于应力完全卸载,故传感器监测不到动应力数据。则列车荷载在路基基床表面的纵向分布长度计算公式为:
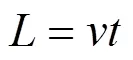
式中:为路基基床表层动应力的纵向影响距离,m;为列车运行速度,m/s;为动应力时程曲线一次完全加载卸载过程所用时间,s。针对于本文所分析的工况,路基基床表层动应力纵向影响范围约为8.8 m。
因此,在对轨道结构进行受力分析时,由于列车荷载所产生的动应力不会发生叠加效应,因此只采用单轴双轮加载即可;而对于路基结构进行受力分析时,由于列车荷载所产生的动应力会在基床结构中产生叠加效应,因此需要使用双轴四轮进行加载。
3 结论
1) 动应力沿轨道路基结构横向都呈现驼峰形,且应力极值均出现在钢轨下方;随着距荷载作用点垂向距离的增加,轨道路基结构各层的竖向应力均逐渐减小;随着深度的增加,动应力的横向分布情况也越均匀。同时在距轨道中心线约1.5 m处,基床表层竖向动应力约等于0,说明路基面宽度取为4 m是合理的。
2) 动应力随着路基深度的增加逐渐减小,在基床表层范围内衰减速度较快,在基床底层范围内衰减速度相对较慢。当取自重应力的20%作为参考标准时,列车荷载在路基中的影响深度为0.75 m。
3) 轨道板和支承层的一次完整应力加载卸载过程由单个轮对作用完成,该应力时程曲线为第1类;而基床表层的一次完整应力加载卸载过程由1个转向架的2个轮对共同作用完成,该应力时程曲线为第2类。路基基床表层动应力的纵向影响范围约为8.8 m。
4) 在对轨道结构进行受力分析时,建议采用单轴双轮加载;而对于路基结构进行受力分析时,建议使用双轴四轮进行加载。
[1] 吴其刚. 现代有轨电车系统发展的重难点及对策研究[J]. 铁道工程学报, 2013, 30(12): 89−92. WU Qigang. Researchon the emphasis and difficulties of modern tramcar system development and its countermeasures[J]. Journal of Railway Engineering Society, 2013, 30(12): 89−92.
[2] LING L, HAN J, XIAO X, et al. Dynamic behavior of an embedded rail track coupled with a tram vehicle[J]. Journal of Vibration & Control, 2016.
[3] 薛富春, 张建民. 移动荷载作用下高速铁路路基动应力的空间分布[J]. 铁道学报, 2016, 38(1): 86−91.XUE Fuchun, ZHANG Jianmin. Spatial distribution of dynamic stresses in embankment of high-speed railway under moving loads[J]. Journal of the China Railway Society, 2016, 38(1): 86−91.
[4] 宋小林, 翟婉明. 高速移动荷载作用下CRTSⅡ型板式无砟轨道基础结构动应力分布规律[J]. 中国铁道科学, 2012, 33(4): 1−7. SONG Xiaoling, ZHAI Wanming. Dynamic stress distribution of the infrastructure of CRTS II slab ballastless track under high speed moving load[J]. China Railway Science, 2012, 33(4): 1−7.
[5] 肖世伟, 雷长顺. 重载铁路路基荷载特征和路基动力响应分析[J]. 铁道工程学报, 2014(4): 51−56. XIAO Shiwei, LEI Changshun. Loading characteristics and dynamic response analysis of subgrade for heavy haul railway[J]. Journal of Railway Engineering Society, 2014(4): 51−56.
[6] Costa P A, Colaço A, Rui C, et al. Critical speed of railway tracks. Detailed and simplified approaches[J]. Transportation Geotechnics, 2015, 2(3): 30−46.
[7] CAI Y, CHEN Y, CAO Z, et al. Dynamic responses of a saturated poroelastic half-space generated by a moving truck on the uneven pavement[J]. Soil Dynamics & Earthquake Engineering, 2015, 69: 172−181.
[8] SUN H, CAI Y, XU C. Three-dimensional simulation of track on poroelastic half-space vibrations due to a moving point load[J]. Soil Dynamics & Earthquake Engineering, 2010, 30(10): 958−967.
[9] BIAN X, JIANG H, CHENG C, et al. Full-scale model testing on a ballastless high-speed railway under simulated train moving loads[J]. Soil Dynamics & Earthquake Engineering, 2014, 66: 368−384.
[10] 刘晶波, 谷音, 杜义欣. 一致黏弹性人工边界及黏弹性边界单元[J]. 岩土工程学报, 2006, 28(9): 1070−1075.LIU Jingbo, GU Yin, DU Yixin. Consistent viscous-spring artificial boundaries and viscous-spring boundary element[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1070−1075.
[11] 邵康, 苏谦, 黄俊杰, 等. 现代有轨电车路基沉降与动应力测试研究[J]. 铁道标准设计, 2017, 61(8): 47−50.SHAO Kang, SU Qian, HUANG Junjie, et al. Study on subgrade settlement and dynamic test of modern tram[J]. Railway Standard Design, 2017, 61(8): 47−50.
Study on dynamic stress distribution law of embedded track subgrade of tram
FENG Qingsong, SUN Kui, LEI Xiaoyan, LUO Kun, LIU Qingjie
(Engineering Research Center of Railway Environmental Vibration and Noise, Ministry of Education, East China Jiaotong University, Nanchang 330013, China)
In order to analyze the dynamic stress distribution law of the embedded track subgrade of tram under the train load, the dynamic model of the modern tram vehicle and a three-dimensional precisely nonlinear track-subgrade-foundation dynamic calculation model were established, and the vertical force of dynamic wheel rail under the irregularity spectrum excitation was obtained. The distribution law of dynamic stress along the transverse, vertical and longitudinal direction of the embedded track subgrade structure under the train load was studied. The results show that under the moving train load, the dynamic stress in the track subgrade exhibits hump shape along the transverse direction and the stress extremum appears below the rail. Secondly, When it is about 1.5 m from the center line of the track, the vertical dynamic stress on the surface of the subgrade is about 0, indicating that the width of the subgrade surface is reasonable for 4 m. Thirdly, When the 20% of self weight stress is taken as the reference standard, the impact depth of the train load in the subgrade is 0.75 m. Finally, When the train speed is 70 km/h, the longitudinal influence range of dynamic stress on the surface of subgrade bed is about 8.8 m.
tram; embedded track; dynamic stress; distribution law; influence depth
10.19713/j.cnki.43−1423/u.2019.04.007
U213.2
A
1672 − 7029(2019)04 − 0885 − 07
2018−05−13
国家自然科学基金资助项目(51668020,51368020)
冯青松(1978−),男,山西榆社人,教授,博士,从事铁路环境振动与噪声和轨道路基动力学研究;E−mail:fqshdjtdx@aliyun.com
(编辑 涂鹏)
