扣件胶垫频变动力性能对钢轨垂向振动特性影响分析
2019-04-26王绍华韦凯杨敏婕胡小刚
王绍华,韦凯,杨敏婕,胡小刚
扣件胶垫频变动力性能对钢轨垂向振动特性影响分析
王绍华1, 2,韦凯1, 2,杨敏婕1, 2,胡小刚1, 2
(1. 西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都 610031; 2. 西南交通大学 土木工程学院,四川 成都 610031)
利用配有温度箱的万能力学试验机,结合温频等效原理与WLF方程的分数阶Zener模型,测试与表征Vossloh300钢轨扣件弹性垫板随频率非线性变化的黏弹性动力性能,并基于有限元方法研究考虑胶垫频变特性对钢轨垂向振动及传递衰减的影响规律。研究结果表明:在双对数坐标系下,扣件胶垫刚度和阻尼系数与频率近似呈线性正相关和负相关。胶垫阻尼频变主要增强中低频范围内的钢轨垂向振动,并能激发出钢轨1阶垂向共振频率;胶垫刚度频变能更准确预测钢轨1阶垂向共振频率;而胶垫频变特性对钢轨pinned-pinned共振频率无影响。考虑胶垫频变特性后,在1阶垂向共振频率以下,钢轨振动在激振点附近快速衰减,超过该频率钢轨振动主要沿钢轨纵向衰减。
扣件胶垫;频变特性;钢轨振动;位移导纳;衰减率
近年来,我国铁路线网和城市轨道交通建设发展如火如荼,但其带来的振动和噪声问题也日渐突出。在减振垫轨道系统结构振动中,扣件弹性胶垫的刚度和阻尼对钢轨振动的影响较大[1−2],而弹性胶垫的动力行为往往随荷载频率呈现非线性变化,体现出动态黏弹性力学特征[3]。在以往轨道动力学研究中大多将扣件弹性胶垫视为定量弹簧−阻尼系统,难以准确描述实际环境下扣件弹性垫板频变动态黏弹性能对钢轨振动特性的影响。显然,为了能够科学地评价钢轨的振动特性,首先需要建立能准确反映轨道系统动力性能的模型。研究发现,钢轨是产生铁路及城市轨道振动噪声的主要振动源,钢轨振动与许多轨道病害产生原因密切相关,如钢轨波磨等[4]。Grassie[5]早期研究得到钢轨导纳主要受轨道系统本身固有特性的影响,因此钢轨的振动特性可以通过获得足够宽激振频率范围内钢轨导纳来分析。在以往对钢轨振动特性研究中,Thompson等[6−8]通过研究发现扣件弹性胶垫刚度对钢轨导纳共振频率影响较大,提出了钢轨导纳主要受截止频率附近轨下垫板阻尼的影响较大。刘洪瑞等[9−11]利用有限元软件分析扣件刚度与阻尼离散取值分别对钢轨导纳的影响,并提出合理的取值范围。而WEI等[12]通过试验得到扣件弹性胶垫刚度和损耗因子都具有频率依赖性。在以往研究分析钢轨振动特性时只分别考虑扣件胶垫刚度或阻尼单一变量的影响,而实际胶垫刚度和阻尼频变特性是相互作用的,未同时考虑扣件胶垫刚度和阻尼的频变特性会不可避免影响对钢轨振动特性的预测精度。鉴于此,本文以Vossloh300扣件弹性垫板为对象,试验测试并理论表征其频率依赖性黏弹性动态性能;以整体道床轨道为例,采用ANSYS大型有限元软件,建立钢轨−扣件系统力学模型,并考虑扣件胶垫非线性频变动力特性,通过计算钢轨跨中受单位简谐激励下在不同拾振点的频率响应,进而准确分析研究扣件胶垫频变性能对钢轨垂向振动及传递衰减的影响规律。
1 扣件胶垫频变力学特性试验
本文将中国高速铁路常用的Vossloh300扣件胶垫作为测试对象,研究其频率依赖性动态性能。由于现有试验条件无法直接测得胶垫的宽频特性,利用温频等效原理,通过配备温度控制范围为−60~20℃(增量为5 ℃)的万能试验机测试大振幅准静态载荷激励(即预压值45 kN,加载幅值30 kN,加载速度30 kN/s,加载频率0.3 Hz)下扣件胶垫的动态性能。并基于以上试验数据,采用Williams-Landel- Ferry(WLF)公式[13]和分数阶Zener模型[14−16]分别预测和表示试验胶垫的宽频动态特性。
1.1 试验设备及结果
在通用万能试验机中,最大载荷为110 kN,试验荷载精度为0.5 kN,测得的位移精度为0.01 mm。温度控制箱可以设定温度范围为−70~120 ℃。试验中钢轨采用短钢轨,往下依次为加载钢板、支承钢板和砂布等配件。
试验按照我国高速铁路扣件系统规范[18]取10次测试结果平均值为最终值,如图1所示,扣件胶垫的动态力−位移曲线大致呈椭圆形,说明其动态力学行为基本上与线性黏弹性材料类似。在线性黏弹性材料的椭圆形滞回曲线中,椭圆横向的斜率为复刚度,外力和相应的压缩位移之间的相位差的切线值为损耗因子。
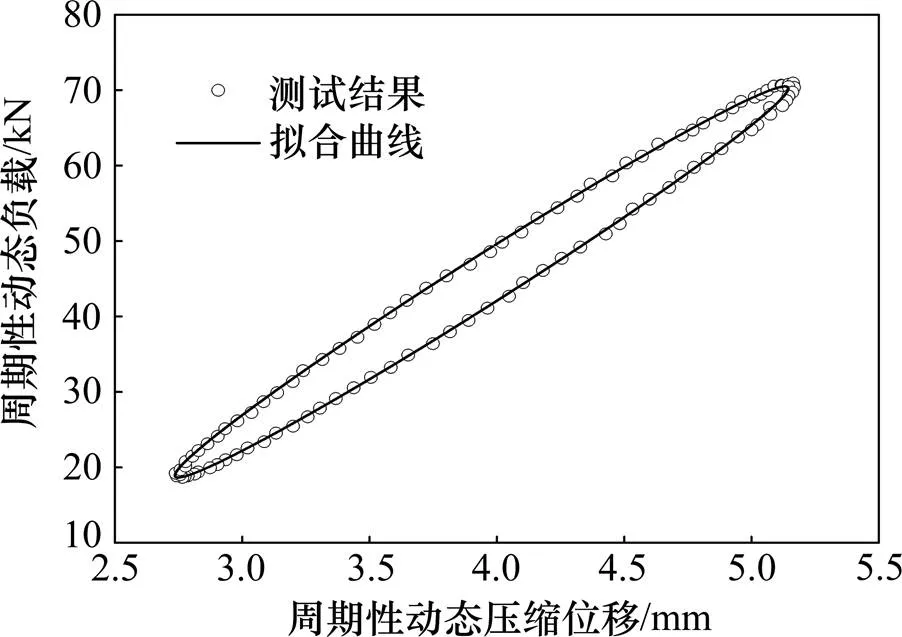
图1 胶垫20 ℃时测试结果和拟合曲线
1.2 温频等效原理及预测结果
根据图3所示,容易得到试验胶垫的储能刚度和损耗因子。随着−45℃以下温度的降低,测试胶垫的储能刚度急剧增加,且损耗因数在−45 ℃时达到最高。因此,Vossloh300胶垫的玻璃转变温度[13]约为−45 ℃。
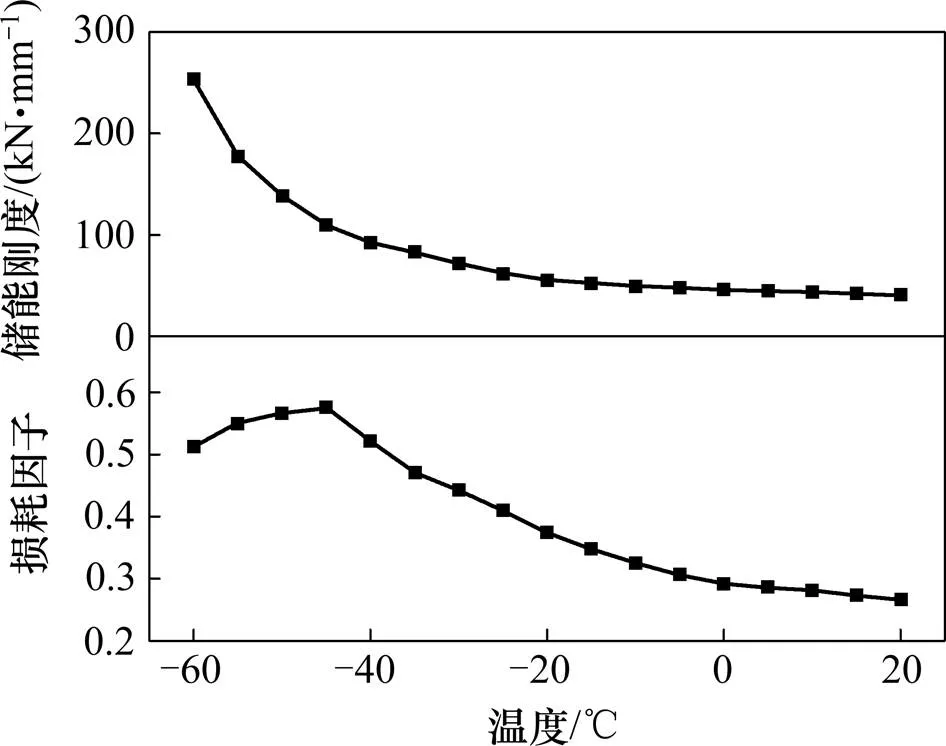
图2 扣件胶垫不同温度下的储能刚度和损耗因子
对于密度为的高分子材料,在频率和开尔文温度下储能刚度′(,)和损耗刚度″(,)可以转化为归一化频率()和参考温度0下储能刚度′[(),0]和损耗刚度″[(),0],转化公式如式(1)~(2)所示。
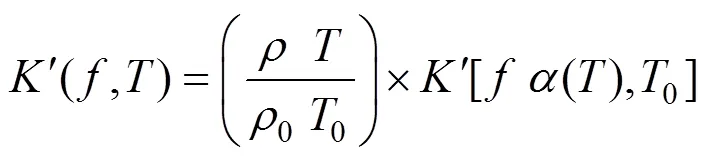
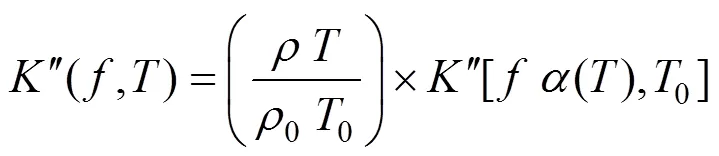
一般来说,温度对高分子材料动态特性的影响远大于频率的影响,动态测量也可以在很宽的温度范围内轻松实现。因此,归化频率()远高于测试频率。换算系数()可以用WLF公式[13]计算,参见式(3)。
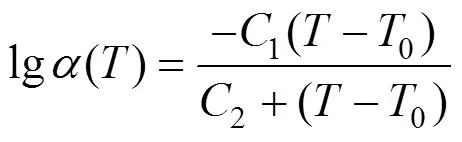
式(3)中:1和2分别为17.44 K和51.6 K,与参考温度0和所用高聚物材料的类型有关,本文参考温度0取玻璃化转变温度。
基于在特定频率和各种低温下的周期性动态测试,WLF公式用于预测Vossloh300轨下胶垫在20℃时在0.1~10 000 Hz范围内的动态特性,如图3所示。
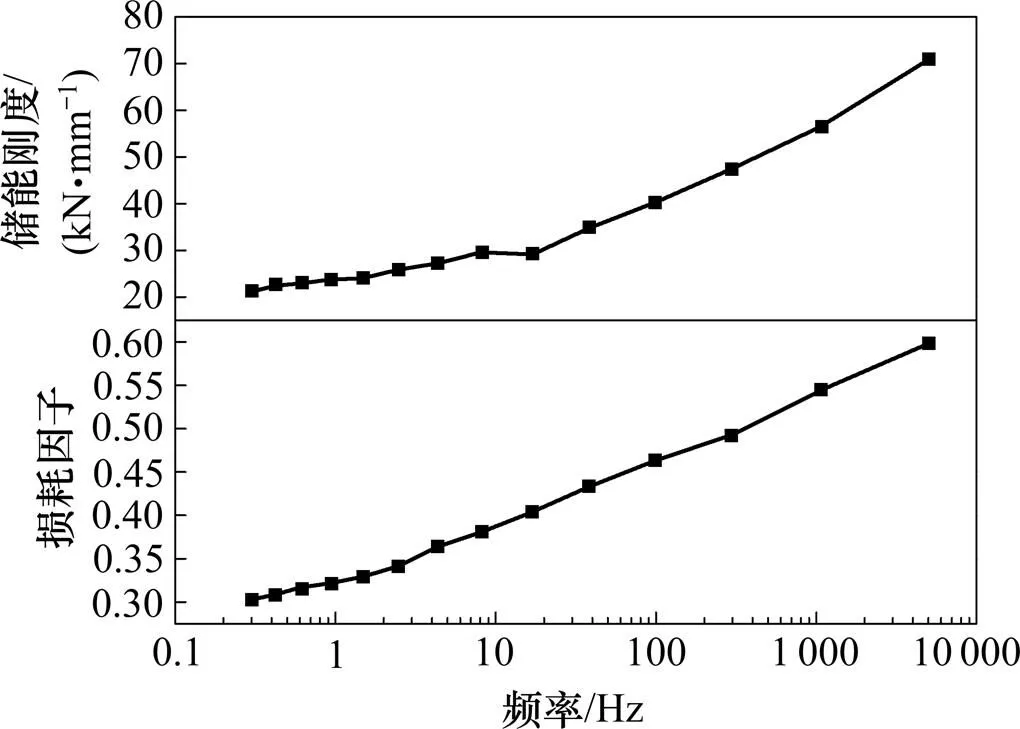
图3 胶垫20℃时宽频范围内的储能刚度和损耗因子
1.3 分数阶Zener模型理论表征结果
通常,线性黏弹性材料的动态力学性能可以用各种分数阶本构模型表示,如分数阶Kelvin-Voigt模型,分数阶Zener模型等[14−16]。分数阶Zener模型能更好地模拟胶垫等橡胶材料动态频率特性,因此在本节中,使用四参数分数阶Zener模型[14, 16]来表示测试胶垫的频变特性,如图4所示。
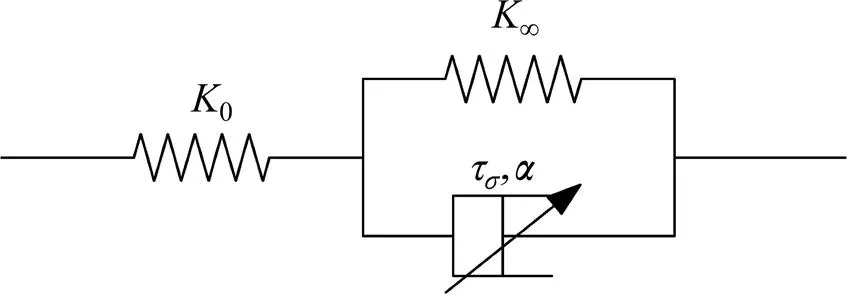
图4 分数阶Zener模型
分数阶Zener模型的时域本构方程为:
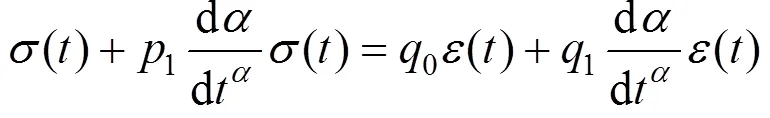
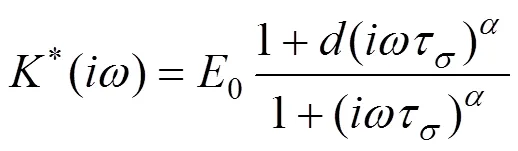
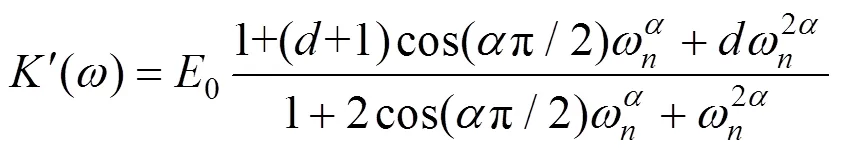
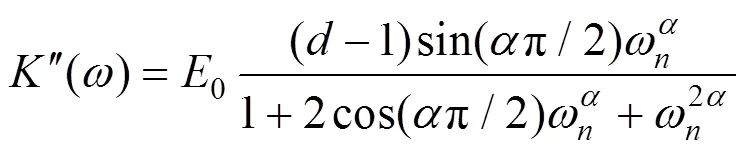
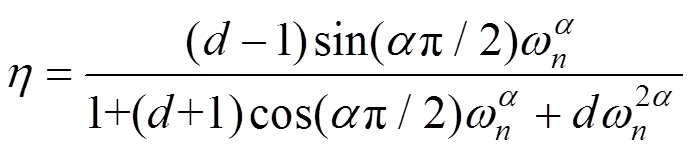
通过最小二乘法,扣件胶垫在20 ℃时在0.1~10 000 Hz范围内的储能刚度和损耗因子基本上可以与分数阶Zener模型拟合(见图5)。表1中列出了20 ℃下大振幅准静态载荷激励加载工况时分数阶Zener模型中的参数。
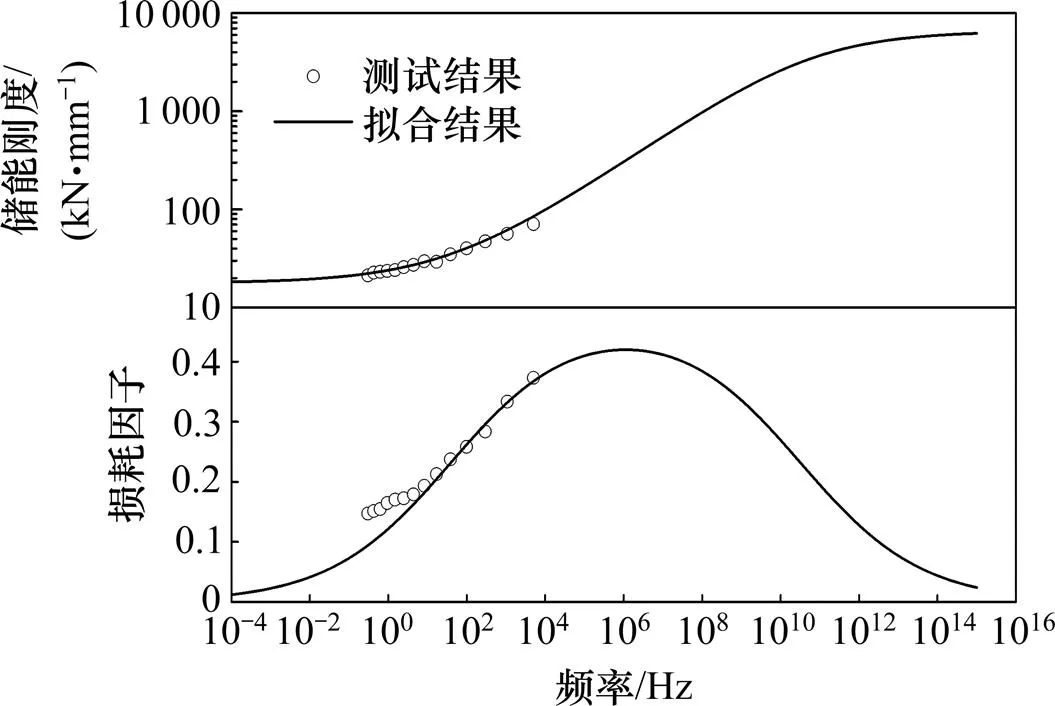
图5 胶垫参数测试结果与拟合结果对比

表1 分数阶Zener模型的参数
根据文献[17],在任一激振频率下,应用分数阶Zener模型在频域中计算得到的储能刚度和损耗因子可以通过式(9)~(10)转化为随频率变化的胶垫刚度和阻尼值。
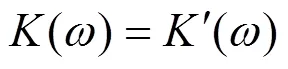
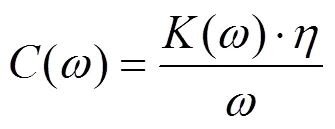
通过计算得到Vossloh300胶垫20 ℃时在1~3 000 Hz范围内刚度和阻尼系数如图7所示。可以看到,在该范围内胶垫刚度和阻尼在双对数坐标系下与频率呈近似线性关系,在激振频率增加10倍时分别平均增加36%和降低81%。
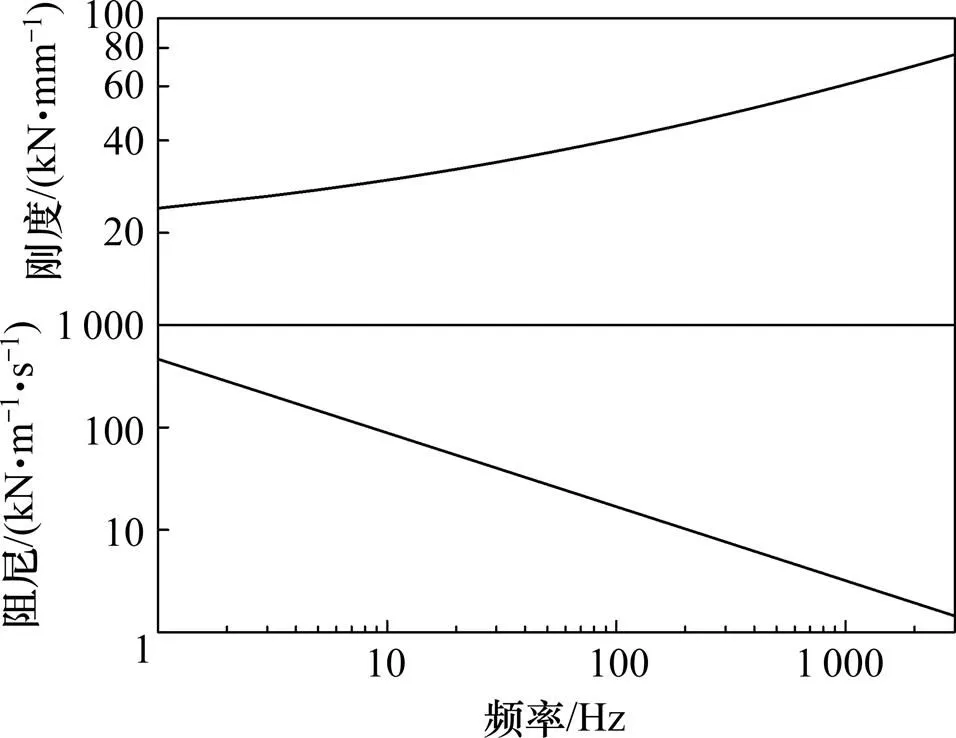
图6 胶垫1~3 000 Hz的刚度和阻尼系数
2 钢轨导纳和衰减率的模型及求解方法
2.1 钢轨垂向位移导纳求解方法
通常,系统的振动特性可以通过获得足够宽激振频率范围内导纳来反映。位移导纳是传导位移的能力,本节采用完全法进行频率响应分析,通过复数代数算法求解一系列耦合的矩阵方程,计算单位力激励下轨道结构的频率响应。轨道系统动力学方程如下:
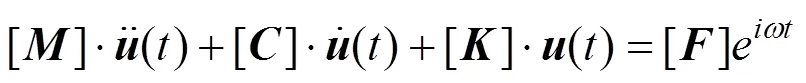
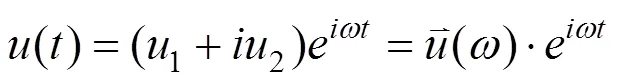
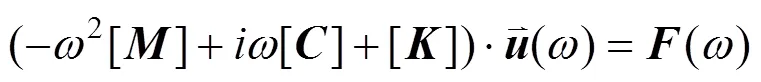
当结构受单位荷载作用时,得到轨道结构的位移导纳求解方程,如式(13)。
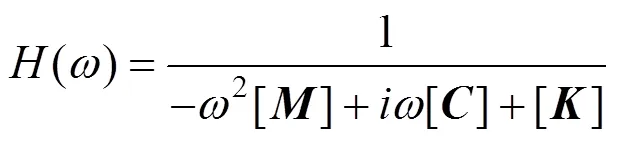
本文采用整体道床无砟轨道,该轨道系统由钢轨、扣件(包括轨下胶垫)、混凝土无砟道床板及混凝土底座等组成。考虑到轨下基础质量很大,且道床板与混凝土底座之间几乎没有弹性,轨道的弹性主要由轨下胶垫提供,因此轨道系统振动主要表现为钢轨振动,在将钢轨视为离散点支承的Timoshenko梁,如图7所示。
图7 整体道床无砟轨道力学模型
Fig. 7 Mechanical model of ballastless track on monolithic track bed
在ANSYS软件中,用Beam188梁单元建立钢轨模型,为减小边界效应,钢轨长度必须足够长,本文采用200跨扣件间距长度进行计算,且确保计算精度,将每跨钢轨划分为30个子单元[11],扣件及轨下胶垫采用弹簧阻尼单元Combin14模拟,轨道系统力学模型参数如表2所示, 其中Vossloh300胶垫常量刚度及阻尼系数为20 ℃时4 Hz下刚度和阻尼取值[18],通过在有限元模型中对钢轨跨中施加单位垂向简谐力激励,求得钢轨激励点和不同拾振点的频率响应。

表2 轨道动力学参数
2.2 钢轨垂向振动衰减率求解
振动衰减率作为结构振动性能的重要判据,反映了振动在结构中的传递规律及其对结构本身的影响,通过计算钢轨振动衰减率来衡量轨道的动力性能。为研究频域内钢轨振动沿纵向的衰减特性,可由计算得到激振点和拾振点的频率响应函数代入式(14)计算确定,拾振点的位置分布是关于扣件间距的函数,拾振点的个数和位置按标准规定的原则选取[19],拾振点位置布置如图8所示。
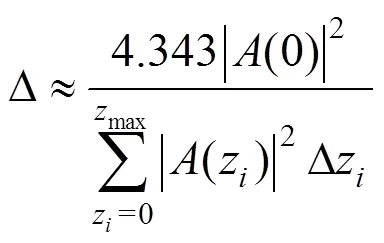
其中:Δ为dB/m为单位的钢轨振动衰减率;Δz为第个拾振点与第+1个拾振点之间的距离;(z)为沿钢轨纵向在z位置的频率响应函数,本文采用位移导纳。
图8 拾振点位置布置
Fig. 8 Pickup point placement
3 扣件胶垫频变特性对钢轨垂向振动特性的影响分析
本节主要讨论扣件胶垫刚度与阻尼频变对钢轨垂向振动特性的影响,各工况如表3所示。其中频变工况为在有限元软件中扫频读取图6所示胶垫各频率点下的刚度和阻尼值,再计算各对应频率点下距跨中激励点不同位置的钢轨垂向位移导纳。

表3 各工况下扣件胶垫动力学参数取值
3.1 钢轨垂向振动位移导纳分析
本节计算了4种工况下1~3 000 Hz范围内钢轨垂向振动位移导纳,结果如图9所示。
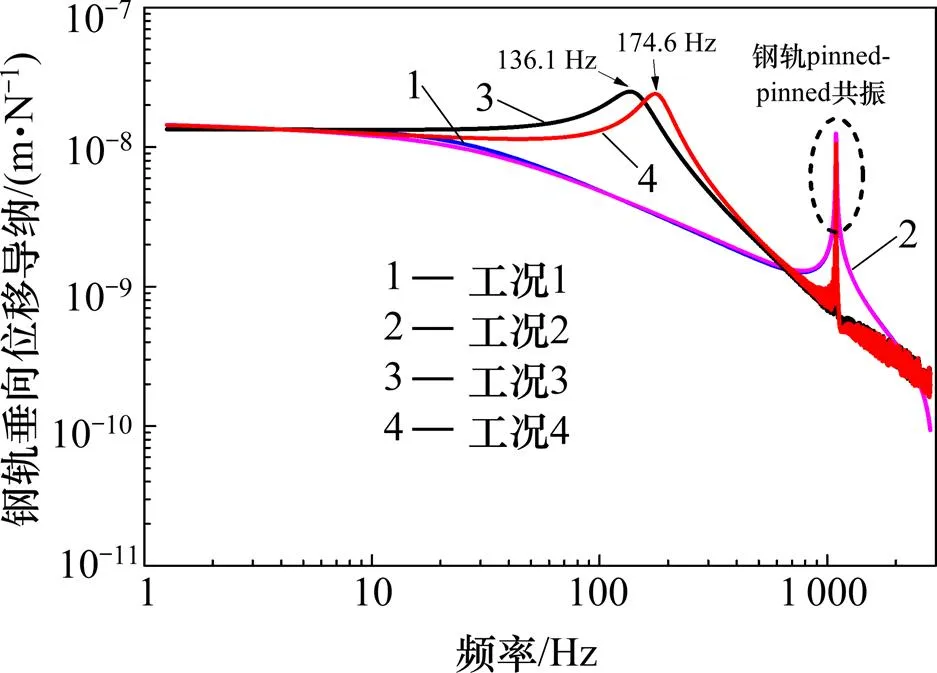
图9 各工况下钢轨垂向位移导纳对比
由图9可知,本文模型中钢轨1阶垂向共振频率点为174.6 Hz。同时根据文献[20]利用有限元模态分析方法考虑胶垫频变特性求解钢轨−扣件系统垂向敏感共振频率,如图10所示,得到钢轨−扣件系统1阶垂向共振频率为174.5 Hz,验证了本节有限元模型的可靠性。
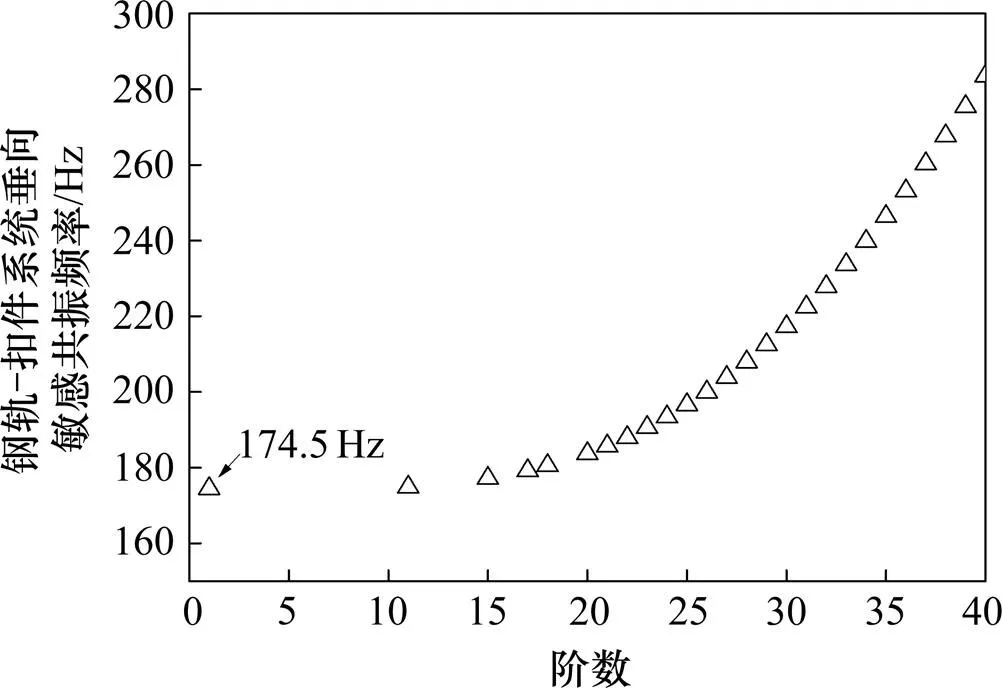
图10 钢轨-扣件系统垂向敏感共振频率
从图9中对比工况1,2和3发现,胶垫刚度频变在50 Hz以下对钢轨垂向振动有略微影响,其影响可以忽略;而胶垫阻尼频变对钢轨垂向位移导纳幅值影响显著,这是因为常量阻尼工况下胶垫阻尼值较大,钢轨−扣件系统共振难以被激起,而实际情况中扣件胶垫阻尼值随频率增大而减小,在钢轨pinned-pinned共振附近及以上中高频范围内钢轨振动出现上下振荡。通过分析工况3和4发现,当在考虑胶垫阻尼频变的基础上分析胶垫刚度频变特性的影响时,发现钢轨−扣件系统在400 Hz以下范围的频带振动向更高频移动,其钢轨1阶垂向共振频率增加了38.5 Hz,这说明钢轨−扣件系统共振主要受胶垫频变阻尼的影响。而对钢轨pinned- pinned振动来说,各工况下钢轨pinned-pinned共振频率基本一致,说明考虑扣件胶垫刚度及阻尼变化均对钢轨pinned-pinned共振频率几乎没有影响。
3.2 钢轨垂向振动传递衰减特性分析
本节主要分析扣件胶垫频变条件下钢轨纵向传递衰减特性以及4种工况下钢轨振动衰减率影响规律研究,结果如图11~12所示。
由图11所示,随着钢轨振动纵向传播距离的增加,考虑胶垫刚度与阻尼频变特性后,在钢轨1阶垂向共振频率以下,钢轨振动衰减较高且稳定,此时钢轨振动在激振点附近快速衰减。衰减率曲线在钢轨1阶垂向共振频率附近出现拐点,由6.7 dB/m迅速减小为3.6 dB/m,并在中高频范围内衰减趋于平缓并以一定的幅度振荡;当距激励点单侧辐射长度为30 m左右时,中高频衰减率均值为0.15 dB/m,且随着纵向距离的增加钢轨振动衰减程度变化很小。
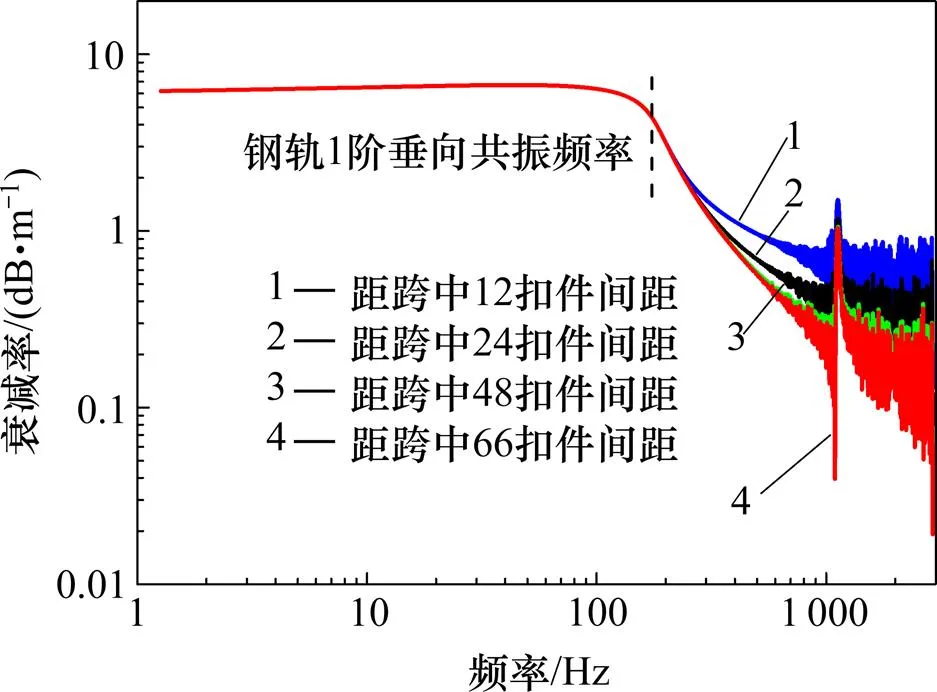
图11 钢轨振动纵向衰减率变化图
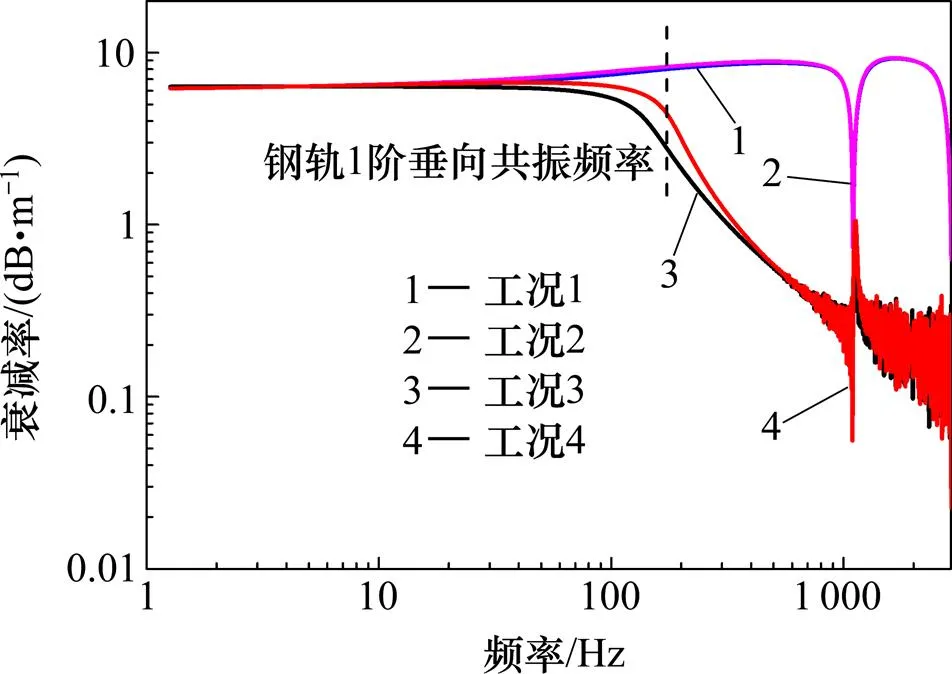
图12 各工况下钢轨振动衰减率对比图
图12所示为选取4种工况下距跨中激励点纵向48个扣件间距拾振点的衰减率分析。不考虑胶垫频变特性情况下,除钢轨pinned-pinned共振附近外,衰减率在其他频带始终保持较高值。考虑扣件胶垫阻尼频变特性,衰减率在钢轨1阶垂向共振频率附近迅速降低,并且主要对中高频范围内钢轨振动衰减影响较大。单独考虑胶垫刚度频变对衰减率影响较小,但在扣件胶垫阻尼频变基础上可以发现,扣件胶垫频变刚度使共振频率附近的高衰减率的频带变宽且幅值略微增大,对中高频振动衰减的影响较小。4种工况下衰减率在钢轨pinned- pinned共振附近均出现峰谷段。
4 结论
1) 当激振频率增加10倍时,Vossloh300扣件胶垫的刚度和阻尼在双对数坐标系下分别近似线性增加36%和降低81%。说明扣件胶垫等高分子材料具有明显的频变特性,在实际环境中胶垫的刚度和阻尼取值并非定量。
2) 胶垫阻尼频变主要增大10~650 Hz范围内的钢轨垂向振动,并加剧钢轨pinned-pinned共振频率附近及以上的钢轨中高频振动响应;在此基础上考虑胶垫刚度频变能更准确预测钢轨1阶垂向共振频率为174.6 Hz,对比不考虑胶垫频变工况增大了38.5 Hz。因此,不考虑胶垫频变特性会降低对钢轨垂向振动特性的预测精度,但扣件胶垫频变特性对钢轨pinned-pinned共振频率几乎没有影响。
3) 在钢轨1阶垂向共振频率以下低频范围内,钢轨振动衰减率保持较高稳定值,且高衰减频率范围主要受胶垫刚度频变的影响;高于该频率,扣件阻尼频变使钢轨振动衰减率迅速降低,但在钢轨pinned-pinned共振频率以上衰减率变化较慢;当距激励点单侧辐射长度为30 m左右时,随着纵向距离的增加钢轨振动中高频衰减程度变化很小。说明考虑胶垫频变特性后,低频范围内钢轨振动在激振点附近快速衰减,而钢轨中高频振动主要沿钢轨纵向衰减。
[1] Vincent N, Thompson D J. Track dynamic behaviour at high frequencies. Part 2: Experimental results and comparisons with theory[J]. Vehicle System Dynamics, 1995, 24(Suppl 1):100-114.
[2] 韦凯, 周昌盛, 王平, 等. 扣件胶垫刚度的温变性对轮轨耦合随机频响特征的影响[J]. 铁道学报, 2016, 38(1): 111−116. WEI Kai, ZHOU Changsheng, WANG Ping, et al. Influence of temperature-dependent stiffness of rail pads on the frequency-domain random vibration of vehicle-track coupled system[J]. Journal of the China Railway Society, 2016, 38(1): 111−116.
[3] Fenander Å. Frequency dependent stiffness and damping of railpads[J]. Proceedings of the Institution of Mechanical Engineers—Part F, 1997, 211(1): 51−62.
[4] 谷永磊, 赵国堂, 王衡禹, 等. 轨道振动特性对高速铁路钢轨波磨的影响[J]. 中国铁道科学, 2016, 37(4): 42−47. GU Yonglei, ZHAO Guotang, WANG Hengyu, et al. Effect of track vibration characteristics on rail corrugation of high speed railway[J]. China Railway Science, 2016, 37(4): 42−47.
[5] Grassie S L. The dynamic response of railway track to high frequency vertical excitation[J]. Journal of Mechanical Engineering Science, 1982, 24(2): 97−102.
[6] Thompson D J, Jones C J C, WU T X, et al. The influence of the non-linear stiffness behaviour of rail pads on the track component of rolling noise[J]. Proceedings of the Institution of Mechanical Engineers Part F: Journal of Rail & Rapid Transit, 1999, 213(4): 233−241.
[7] Ryue J, Thompson D J, White P R, et al. Decay rates of propagating waves in railway tracks at high frequencies[J]. Journal of Sound & Vibration, 2009, 320(4): 955−976.
[8] Thompson D J. Railway noise and vibration: mechanisms, modeling and means of control[M]. UK: Elsevier, 2009.
[9] 刘洪瑞, 邹锦华, 王荣辉. 轨道交通橡胶浮置板式轨道结构动力设计参数研究[J]. 铁道科学与工程学报, 2009, 6(2): 5−11. LIU Hongrui, ZOU Jinhua, WANG Ronghui. Dynamic design parameters of rubber floating slab track structure for urban mass transit[J]. Journal of Railway Science and Engineering, 2009, 6(2): 5−11.
[10] 方锐, 肖新标, 房建英, 等. 轨道结构参数对钢轨和轨枕振动特性的影响[J]. 铁道学报, 2011, 33(3): 71−76. FANG Rui, XIAO Xinbiao, FANG Jianying, et al. Effect of structure parameters of railway track dynamic behavior of rail and sleeper[J]. Journal of the China Railway Society, 2011, 33(3): 71−76.
[11] 孙方遒, 谷爱军, 刘维宁. 钢轨长实体模型在不同频段的振动及传递特性分析[J]. 铁道学报, 2013, 35(2): 81−86. SUN Fangxuan, GU Aijun, LIU Weining. Study on vibration and transmission characteristics of long solid rail models under different frequencies[J]. Journal of the China Railway Society, 2013, 35(2): 81−86.
[12] WEI Kai, YANG Qilu, DOU Yinling, et al. Experimental investigation into temperature-and frequency-dependent dynamic properties of high-speed rail pads[J]. Construction & Building Materials, 2017, 151: 848−858.
[13] Doolittle A K. Studies in Newtonian Flow. II. The dependence of the viscosity of liquids on free-space[J]. Journal of Applied Physics, 1951, 22(12):1471−1475.
[14] Kim T H, Pinkham J T, Heninger S J, et al. A theoretical basis for the application of fractional calculus to viscoelasticity[J]. Journal of Rheology, 2000, 27(2): 115− 198.
[15] Pritz T. Five-parameter fractional derivative model for polymeric damping materials[J]. Journal of Sound & Vibration, 2003, 265(5): 935−952.
[16] 赵永玲, 侯之超. 基于分数导数的橡胶材料两种黏弹性本构模型[J]. 清华大学学报(自然科学版), 2013, 53(3): 378−383. ZHAO Yongling, HOU Zhichao. Two viscoelastic constitutive models of rubber materials using fractional derivations[J]. Journal of Tsinghua University (Science and Technology), 2013, 53(3): 378−383.
[17] Maes J, Sol H, Guillaume P. Measurements of the dynamic railpad properties[J]. Journal of Sound and Vibration, 2006, 293: 557−565.
[18] TB/T 3395.1—2015, 高速铁路扣件第一部分: 通用技术条件[S]. TB/T 3395.1—2015, Fastening systems for high-speed railway Part 1: General requirement[S].
[19] 孙晓静, 张厚贵, 刘维宁, 等. 轨道系统钢轨振动衰减率动力测试研究[J]. 铁道工程学报, 2015, 32(7): 34− 39. SUN Xiaojing, ZHANG Hougui, LIU Weining, et al. Test research on the characterizing the dynamic damping behavior of track structure[J]. Journal of Railway Engineering Society, 2015, 32(7): 34−39.
[20] 韦凯, 张攀, 梁迎春, 等. 扣件胶垫刚度频变的钢轨垂向自振特征分析[J]. 铁道学报, 2016, 38(6): 79−85. WEI Kai, ZHANG Pan, LIANG Yingchun, et al. Study on vertical natural vibrations of steel rail considering frequency-dependent stiffness of rail rads[J].Journal of the China Railway Society, 2016, 38(6):79−85.
Influence of frequency-dependent dynamic properties of rail pad on vertical vibration characteristics of rail
WANG Shaohua1, 2, WEI Kai1, 2, YANG Minjie1, 2, HU Xiaogang1, 2
(1. MOE Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)
In this paper, the frequency-dependent dynamic properties of the rail pad of the Vossloh 300 fastener were tested by universal mechanic machine and temperature box, which characterized by the temperature- frequency equivalent principle and the fractional-order Zener model of the WLF equation. Then the influence of the frequency-dependent properties of the rail pad on the vertical vibration and transmission attenuation of the rail was analyzed based on the finite element method. The results show that: In the double logarithmic coordinate system, the stiffness and damping coefficient of the rail pad are linearly positively or negatively correlated with the frequency. The frequency-dependent damping of the rail pad mainly enforces the vertical vibration of the rail in the middle and low frequency range, which excites the first-order vertical resonance frequency of the rail. The frequency-dependent stiffness of the pad can predict the first-order vertical resonant frequency of the rail more accurately. The pinned-pinned resonance frequency of the rail is not affected by the frequency change characteristics of the pad. Considering the frequency-dependent dynamic properties of the rail pad, the rail vibration below the first-order resonance frequency of rail could reduce near the excitation point, while high frequency vibration of rail will not attenuate rapidly and spread along the rail in a long distance.
rail pad; frequency-dependent dynamic properties; rail vibration; displacement admittance; decay rate
10.19713/j.cnki.43−1423/u.2019.04.008
U211.3
A
1672 − 7029(2019)04 − 0892 − 08
2018−05−29
国家自然科学基金资助项目(51608460,51578468)
韦凯(1980−),男,山西临汾人,研究员,博士,从事轨道系统动力学及环境振动噪声问题研究;E−mail:wei_mike@163.com
(编辑 涂鹏)
