汽车撞击与爆炸复合作用下H型钢柱损伤效应分析

田 力，毛祖杰



汽车撞击与爆炸复合作用下H型钢柱损伤效应分析

田 力1, 2，毛祖杰1

(1. 天津大学建筑工程学院，天津 300072；2. 滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300072)

为研究H型钢柱在汽车撞击与爆炸复合作用下的抗冲撞与抗爆性能，本文基于非线性分析有限元软件ANSYS/LS-DYNA，通过建立汽车先撞击钢柱后爆炸的全过程模型来模拟汽车撞击与爆炸的复合作用对H型钢柱的损伤破坏．本文对比分析了汽车撞击单独作用、爆炸荷载单独作用与二者复合作用3种工况下H型钢柱动态响应的差异性．同时，采用参数化分析方法，探究H型钢柱在汽车撞击与爆炸复合作用下，轴压比、长细比、钢材强度和截面类型等因素对于钢柱损伤效应的影响．结果表明：汽车撞击偏转致使前翼缘两侧位移差异显著，质心偏移一侧明显高于另一侧；爆炸冲击造成前翼缘两侧位移较为对称，整体位移相对较大．冲击波因汽车的阻挡作用发生反射与绕流现象，致使钢柱因爆炸产生的动力响应减弱．为保证H型钢柱的抗冲撞与抗爆性能，应限制其轴向压力值，若钢材强度选用Q390，则轴压比宜控制在0.4以内．若原选用钢材强度较小，适当提高强度可提升钢柱抗冲撞与抗爆性能，但不能盲目提高．改变长细比对钢柱的抗冲撞与抗爆性能影响较小．在保持柱高与总用钢量一致的前提下，圆形空心型截面钢柱的抗冲撞与抗爆性能最优，H型截面钢柱次之，方形空心型截面钢柱最差且与前两者差距较大．本文研究成果可为后续钢柱抗冲撞与抗爆防护措施的研究提供理论基础．

汽车撞击；爆炸；复合作用；钢柱；损伤效应

近年来，随着我国经济和近现代工业化的发展，工业产品的运输愈加频繁，其中不乏一些危险化学品和易燃易爆品的运输，而且，近些年危险品运输车辆的爆炸事故也是时有发生．由于钢结构具有刚度大、自重较轻、综合经济指标好等特点而被广泛应用于民用与工业建筑．在钢结构抗冲撞与抗爆设计和防护措施研究中，由于钢柱是钢结构的重要竖向承重体系，是保证结构整体稳定的重要构件，因此对其进行抗冲撞与抗爆研究是至关重要的．也可借此研究为后续钢柱抗冲撞与抗爆防护措施研究提供理论基础.

由于载有易燃易爆品汽车先撞击后爆炸整个过程的复杂性，对于这种复合作用下钢柱损伤效应分析的研究鲜见报道．已有的研究主要是针对汽车撞击荷载或者爆炸荷载中的某一单独作用进行分析研究的．尹越等[1]采用 ABAQUS 建立有限元模型，对车辆撞击钢结构人行天桥钢柱进行分析，通过位移等效分析，得到了小型车辆和大型车辆撞击等效静力荷载的计算公式；丁阳等[2]通过位移、剩余竖向承载力和钢柱最大剪力指标，研究了爆炸荷载作用下钢柱的损伤评估和失效分析；李月强等[3]对简支钢柱承受爆炸荷载时的动力响应进行模拟，研究分析SDOF模型的适用范围；张秀华等[4]分析了焊接工字形钢梁在爆炸荷载作用下破坏模式及影响动力响应的主要因素；杨涛春等[5]通过数值计算和试验数据相结合，总结了爆炸荷载对于不同翼缘钢柱的水平及竖向分布形式，并给出工字形钢柱上爆炸作用的确定方法．

本文将通过非线性有限元软件ANSYS/LS-DYNA模拟汽车撞击与爆炸复合作用对于H型钢柱的损伤破坏．对比分析汽车撞击单独作用、爆炸荷载单独作用与二者复合作用3种工况下钢柱的动态响应与损伤效应的差异性．通过参数化分析方法，探究汽车撞击与爆炸复合作用下轴压比、长细比、钢材强度和截面类型等因素对H型钢柱损伤效应的影响．

1 有限元模型及数值分析方法

1.1 模型简介

为研究H型钢柱在汽车撞击与爆炸二者复合作用下的动态响应与损伤破坏，本文借助有限元软件ANSYS/LSDYNA建立了汽车撞击与爆炸全过程模型，整体模型详见图1．钢柱柱高为3000mm，截面尺寸为300mm×300mm×10mm×15mm×13mm(××1×2×)[6]，钢柱截面形式见图2．

为使模拟结果更接近实际工况，本文在钢柱模型两端各建立了柱头与柱脚[7]，高度均为200mm．柱脚的边界条件设置为固定端，柱头的边界条件仅约束水平方向上的位移．对于实际工况中柱所承受的竖向荷载，通过在柱顶面施加均布面荷载来模拟．本文第4.1节中较为详细地说明了轴向极限稳定承载力p以及轴压比合理范围内的最大值0.4的确定．汽车模型选用的是美国“国家碰撞分析中心”提供的有限元模型，该汽车模型的有效性已经经过了试验的对比验证[8]，汽车有限元模型如图1所示．炸药采用正方体硝酸铵油炸药，边长为476mm，爆心距刚性地面1000mm，质量为100kg，采用中心起爆方式．通过载有炸药的汽车先撞击钢柱再爆炸来模拟汽车撞击与爆炸的复合作用．刚性地面采用关键字*RIGID_WALL_ PLANER来模拟．

由于汽车爆炸位置大致位于汽车中心，考虑时间效率，借鉴文献[9]的做法，将空气域的尺寸取为3204mm×2170mm×3000mm，对空气设定无反射透射边界，空气单元采用渐变式网格尺寸，最小网格尺寸为29.75mm．在有限元全过程计算模型中，钢柱、炸药、空气均采用实体单元Solid164模拟．汽车采用实体单元Solid164、壳单元Solid163和梁单元Solid161模拟．

炸药单元网格尺寸为29.75mm，钢柱最小单元网格尺寸为2.8mm．炸药和空气总单元数约为47×104，钢柱总单元数约为6×104．对钢柱和汽车采用Language算法，炸药和空气采用ALE算法．

图1 全过程计算模型

H—腹板宽度；B—翼缘宽度；t1—腹板厚度；t2—翼缘厚度； r—圆角半径

1.2 数值分析方法

为更加精确有效地模拟汽车先撞击后爆炸的全过程，本文基于ANSYS/LSDYNA中的完全重启动技术，采用全过程分阶段分析方法．全过程共分为4个阶段，分别为竖向荷载施加稳定阶段、汽车撞击阶段、炸药爆炸阶段与自由响应阶段．

在第1阶段(竖向荷载施加稳定阶段)，在施加重力荷载与柱顶均布面荷载后，使柱静置自主达到稳定状态．

在第2阶段(汽车撞击阶段)，运用完全重启动技术继承第1阶段末钢柱的应力与应变．将汽车与钢柱间的接触设置为点面接触，汽车自身以及汽车与刚性地面间采用自动单面接触．接触刚度缩放因子设置为1.0．

在第3阶段(炸药爆炸阶段)，运用完全重启动技术继承第2阶段末钢柱的应力与应变．采用罚函数的流固耦合算法模拟炸药爆炸后冲击波的传播以及对汽车和钢柱的破坏作用．时间步长缩放因子设置为0.67．

在第4阶段(自由响应阶段)，运用完全重启动技术继承第3阶段末钢柱的应力与应变．由于至此阶段，汽车撞击作用与爆炸冲击波作用基本已完全结束，为节省计算时间，本阶段仅计算钢柱的自由响应.

1.3 材料本构模型及参数

空气采用*MAT_NULL模型及*EOS_LINEAR_POLYNOMIAL状态方程描述，其状态方程表达式为

表1 空气的材料参数

Tab.1 Materialpropertiesof air

铵油(ANFO)炸药采用*MAT_HIGH_ EXPLOSIVE_BURN模型及JWL状态方程描述，其状态方程表达式为

钢柱材料采用JOHNSON_COOK本构模型，该模型因其物理意义明确、易于试验拟合、通用性强等特点而被广泛用于金属在大变形、高应变率和高温情况下的材料本构模型，其表达式为

在数值模拟时，考虑到大变形可能会导致单元畸变，故引入了失效准则．JOHNSON_COOK本构模型的失效准则可表示为

表2 炸药的材料参数

Tab.2 Materialpropertiesof ANFO

表3 钢材的材料参数

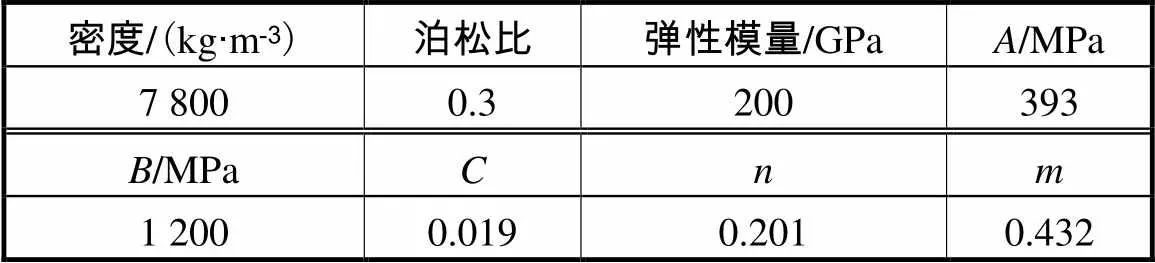
Tab.3 Materialpropertiesof steel

2 有限元模型有效性验证

本文希望通过模拟和对比已有试验的方式来说明文中所采用的耦合算法、接触类型和材料模型的合理性．但截至目前国内外都鲜有钢柱在汽车撞击与爆炸荷载二者复合作用下的破坏试验，故本文采取分别对钢柱落锤撞击试验、钢柱爆炸试验进行数值模拟验证的方式，来间接说明计算模型的合理性．

2.1 钢柱落锤撞击试验验证

崔娟玲等[10]研究了两种不同边界约束条件下的热轧 H 型钢柱侧向冲击试验，获得了试件的破坏形态和残余变形量．

试验梁的截面尺寸HW100×100×6×8．材料为Q235-B，高度为1.5m，具体尺寸如图3所示．在H型钢柱两端均焊接端板，且在下端板处设置了2个三角形加劲肋．落锤总重为150.04kg．本节对试验中落锤高度为2m的工况进行了数值模拟分析．

图3 试件GM-2尺寸

本节中以试验前后钢柱高度中部位置上翼缘外边缘的位移变形值作为试件的局部残余变形量，以试验前后钢柱高度中部位置的中轴线相对位置变化作为试件的整体残余变形量．根据文献[10]可知，落锤高度为2m的试件GM-2的局部残余变形量、整体残余变形量分别为4.85mm、4.76mm．由图4可知数值模拟的局部残余变形量为5.00mm、整体残余变形量为4.68mm．通过对比钢柱落锤试验和数值模拟的结果可以发现，局部残余变形量数值模拟误差为3.09%、整体残余变形量数值模拟误差为1.68%，、两参数的数值模拟与试验结果较为吻合．图5为试件GM-2试验与模拟冲击力时程曲线对比，由图可知试件GM-2的数值模拟冲击力峰值为404.69kN，冲击时间为15.49ms．根据文献[10]可知，试件GM-2的冲击力峰值为422.48kN，冲击时间为14.64ms，故冲击力峰值模拟误差为4.21%，冲击时间模拟误差为5.81%．而且，GM-2数值模拟冲击力时程曲线与试验曲线较为吻合，变化趋势基本一致．图6为试件GM-2试验与模拟落锤冲击后变形对比图，由图可知试验与模拟冲击后钢柱变形模式和趋势都较为吻合．因此，本文采用的钢柱数值模型能较好地模拟钢柱承受的撞击作用．

图4 试件GM-2残余变形量时程曲线

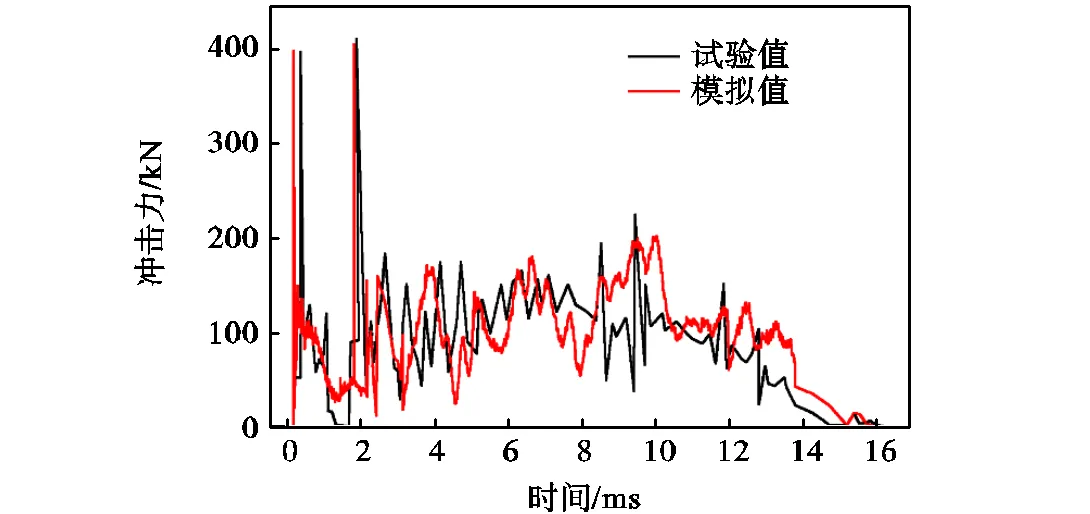
图5 试件GM-2试验与模拟冲击力时程曲线对比

图6 试件GM-2试验与模拟冲击后变形对比

2.2 钢柱爆炸试验验证

Nassr等[11]对钢柱在爆炸作用下的动态响应进行了试验研究．本节对试验中的典型工况4进行数值模拟对比验证．

试验工况4中，钢柱截面为W150×24，柱高2413mm，两端各焊接24.5mm厚钢板，如图7所示．钢柱试件边界条件为一端铰支，另一端辊支，如图8所示．炸药总质量250kg，由10包25kg铵油炸药组成，并放置成棱柱状，炸药到钢柱距离为7m．建模方法、接触类型、耦合算法及材料模型等均采用本文第1节中的设置．如图9所示，数值模拟钢柱跨中挠度曲线与试验挠度曲线变化趋势大致相近，且于＝6ms时，跨中最大挠度值为110.46mm，与文献[11]中试验4的钢柱跨中最大挠度值109.35mm相差1.02%．因此，本文采用的钢柱数值模型能较好地模拟钢柱承受的爆炸荷载作用．

图7 试件尺寸示意

图8 试验装置整体示意

图9 试验与模拟的钢柱跨中位移时程曲线对比

3 汽车撞击作用和爆炸作用及两者复合作用对钢柱损伤效应的比较

本文对4种典型工况进行了数值模拟，如表4所示，以探究钢柱分别在汽车撞击单独作用、爆炸单独作用和二者复合作用下，H型钢柱动态响应和损伤效应的异同．

表4 数值模拟工况

Tab.4 Numericalsimulation conditions

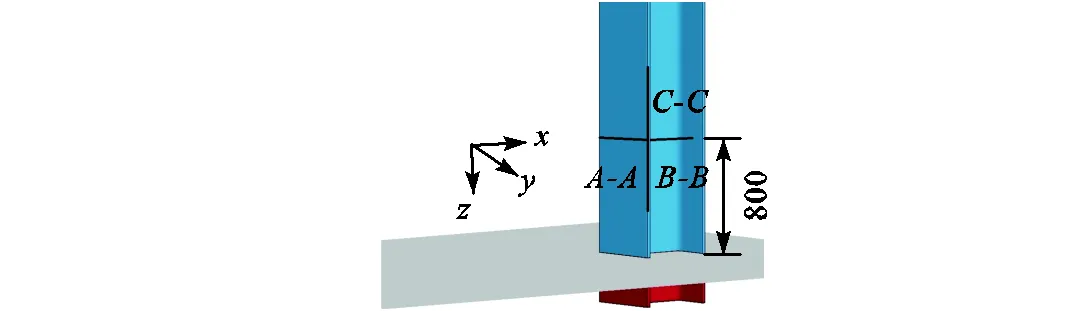
图10 截面A-A、B-B和C-C位置示意

3.1 复合载荷损伤效应分析

由表5可知，对于炸药起爆后冲击波抵达钢柱时间以及超压峰值时间，Model-2和Model-3十分接近；对于超压峰值的大小，Model-3较Model-2略有提高，这是由于爆炸冲击波经过后挡风玻璃、车身和前挡风玻璃这条相对封闭的传播通道时会产生冲击波局部增强效应．

表5 数值模拟工况对比

Tab.5 Comparisonof numerical simulation conditions

分析图11可知，爆炸单独作用下钢柱获得的动能整体大于复合荷载作用下获得的动能，这是由于在汽车撞击与爆炸复合荷载作用下，汽车位于爆炸冲击波传播路径上，且汽车为体积较大的壳体结构．在爆炸冲击波的传播过程中冲击波会与汽车发生相互作用，冲击波会因此发生反射和绕流等现象，且会为此消耗部分冲击波能量，以导致传递至钢柱的动能减少.

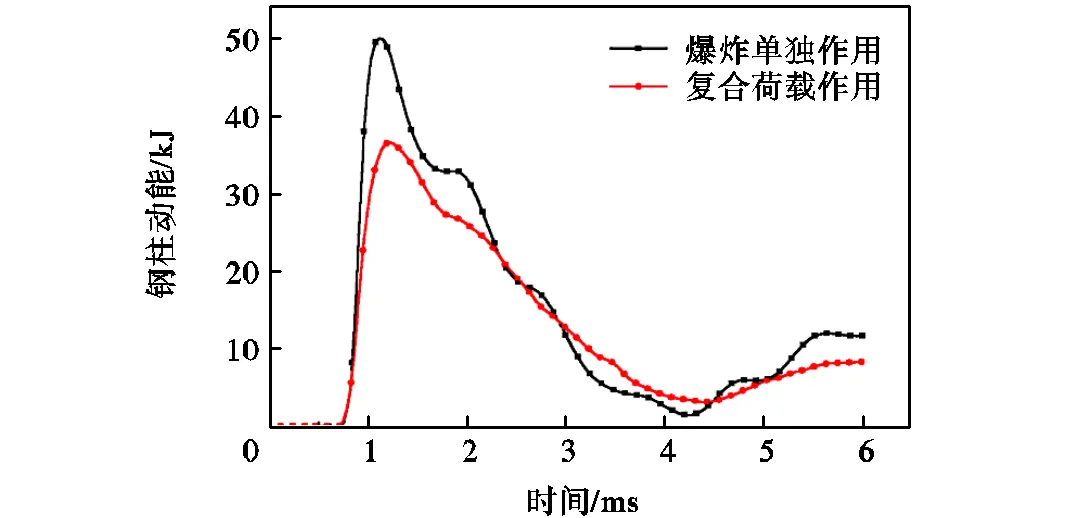
图11 爆炸单独作用与复合荷载作用下钢柱动能时程曲线

3.2 位移响应对比分析

结合钢柱峰值位移(见图12)与塑性应变云图(图13)可知：Model-1中汽车撞击产生的峰值位移整体相对较小，由于车身底部一侧有一个大体积油箱，导致汽车质心偏离其几何中心，从而汽车撞击钢柱过程中会发生单侧偏转，质心偏移一侧的钢柱前翼缘峰值位移明显大于另一侧．Model-2中爆炸冲击波作用造成的钢柱前翼缘峰值位移整体相对较大，且峰值位移曲线相对于Model-1中汽车撞击产生的峰值位移曲线更为平滑；Model-3中汽车偏转一侧的钢柱前翼缘复合作用峰值位移曲线明显大于汽车撞击、爆炸单独作用下的峰值位移曲线；而另一侧前翼缘由于汽车撞击对复合作用峰值位移贡献很小，且由于汽车对于爆炸冲击波的传播有绕流与耗能作用，故该侧复合作用下的峰值位移曲线略小于爆炸冲击波单独作用下的峰值位移曲线．正因为存在汽车的绕流与耗能作用，复合作用峰值位移曲线整体小于Model-4中汽车、爆炸冲击波单独作用下的峰值位移的线性叠加．

图12 前翼缘截面A-A处x方向峰值位移

（a）汽车撞击单独作用（b）爆炸单独作用（c）复合荷载作用

4 汽车撞击与爆炸复合作用下H型钢柱损伤效应的参数化分析

4.1 轴压比

钢柱作为钢结构的重要竖向承重体系，是保证结构整体稳定的重要构件，因此，竖向承载能力在钢柱的性能中尤为重要．轴压比是柱的轴向压力与轴向极限稳定承载力p的比值．本节选取轴压比为0.2、0.3、0.4、0.5、0.6、0.7这6种工况，分析在相同汽车撞击与爆炸复合作用下的钢柱损伤效应，以研究轴向压力对钢柱抗冲撞与抗爆性能的影响．为明确钢柱的轴向极限稳定承载力p，本文建立钢柱竖向承载力数值模型．柱脚设置为固定端，柱头仅约束水平方向的位移，并在柱顶面缓慢施加均布面荷载．可根据柱顶节点的竖向位移变化来明确钢柱的极限破坏状态，由图14可知，当竖向荷载为8000kN时，柱顶竖向位移急剧增加，此时即为钢柱的极限破坏状态．从而即可间接确定钢柱的轴向极限竖向承载力为p＝8000kN．

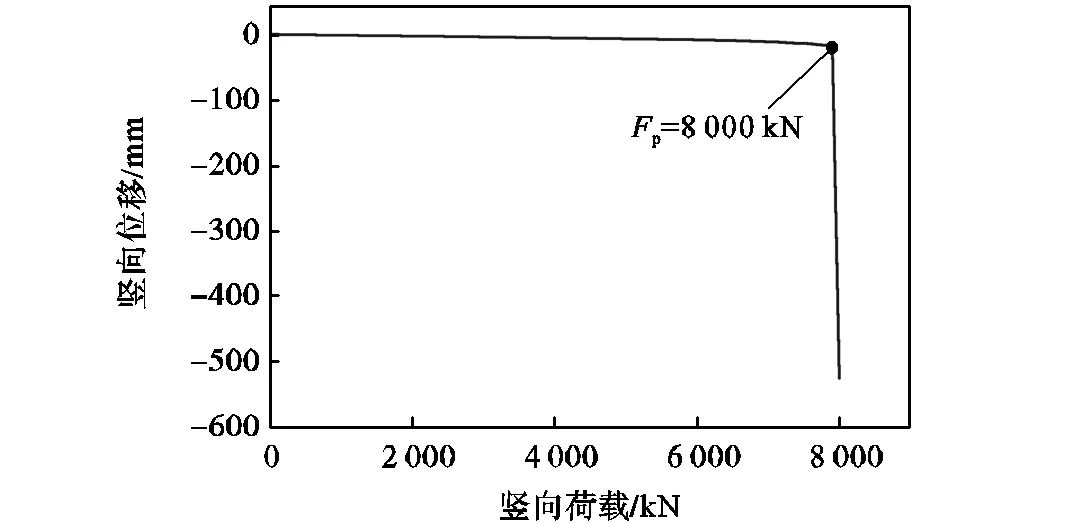
图14 柱顶节点的竖向位移时程曲线

图15反映的是不同轴压比下，在相同汽车撞击与爆炸复合作用下不同钢柱的塑性应变云图对比.分析图15可知，当轴压比控制在0.4以内时，钢柱的翼缘在复合荷载作用下，局部发生较明显的弯曲变形，但腹板仍未出现明显的屈曲变形，说明其仍具备一定的继续承载能力．而当轴压比为0.5、0.6和0.7时，翼缘和腹板均已发生明显的屈曲变形，已不具备继续承载的能力．

图15 不同轴压比下钢柱塑性应变云图对比

图16显示的是不同轴压比下钢柱前翼缘截面-处方向和截面-处方向、腹板截面处方向的峰值位移．由图中可知：前翼缘截面处方向、截面处方向和腹板截面处方向的峰值位移随着轴压比的增加呈非线性增长．当钢柱轴压比不大于0.4时，前翼缘截面处、截面处和腹板截面处的变形位移包络图曲线较为接近．而轴压比为0.5时，截面处峰值位移较轴压比为0.4时增加了30.08%，截面处峰值位移较轴压比为0.4时增加了28.17%，截面处峰值位移较轴压比为0.4时增加了28.91%；而轴压比为0.6时，截面处峰值位移较轴压比为0.4时增加了66.22%，截面处峰值位移较轴压比为0.4时增加了83.43%，截面处峰值位移较轴压比为0.4时增加了66.02%．因此，轴压比大于0.4时，前翼缘截面处方向和截面处方向、腹板截面处方向的峰值位移随着轴压比的增加而急剧增长，且增速也随之增快．因此，在抗冲撞与抗爆设计中，应控制钢柱轴向压力设计值的大小．钢材强度等级为Q390时，轴压比宜控制在0.4以内．

4.2 长细比

为探究在汽车撞击与爆炸复合荷载作用下，不同长细比对钢柱损伤效应的影响，本节在保持截面类型和截面尺寸相同的情况下，钢材强度为Q390，为更明显体现不同长细比的钢柱的变形差异，轴向压力取0.4p＝3200kN，并通过改变钢柱柱高来改变长细比．本节分别选用柱高为2.7m(长细比20.61)、3.0m(长细比22.90)、3.3m(长细比25.19)、3.6m(长细比27.48)、3.9m(长细比29.77)、4.2m(长细比32.06)和4.5m(长细比34.35)这7种工况进行数值模拟．图17为7种不同柱高的钢柱截面处和截面处方向、截面处方向的峰值位移．

图16 不同轴压比下钢柱前翼缘和腹板峰值位移

从图17可知，在复合荷载作用下，不同长细比的钢柱截面处方向和截面处方向的位移包络图轮廓基本接近，变化幅度很小．在汽车撞击与炸药起爆高度附近(距地1000mm)，截面处方向的位移包络图轮廓也较为接近．而在钢柱较高位置处，各钢柱同一高度的处方向峰值位移差异较为明显，例如在2.7m高度处的峰值位移，长细比25.19的钢柱较长细比22.90的钢柱增长了60.9%，长细比27.48的钢柱较长细比25.19的钢柱增长了45.6%，长细比29.77的钢柱较长细比27.48的钢柱增长了18.2%，长细比32.06的钢柱较长细比29.77的钢柱增长了5.4%，长细比34.35的钢柱较长细比32.06的钢柱增长了14.4%．因此，可得出如下结论：对于汽车撞击与爆炸作用等短时间冲击荷载，集中作用区域的钢柱局部破坏现象较为明显，但长细比的改变对其影响较小．而在钢柱的较高位置，与集中作用区域有一定距离处，各钢柱同一高度处的截面处方向峰值位移随着长细比的增大而增大，位移增速也随之呈变缓趋势，故应尽量选用长细比较小的钢柱．

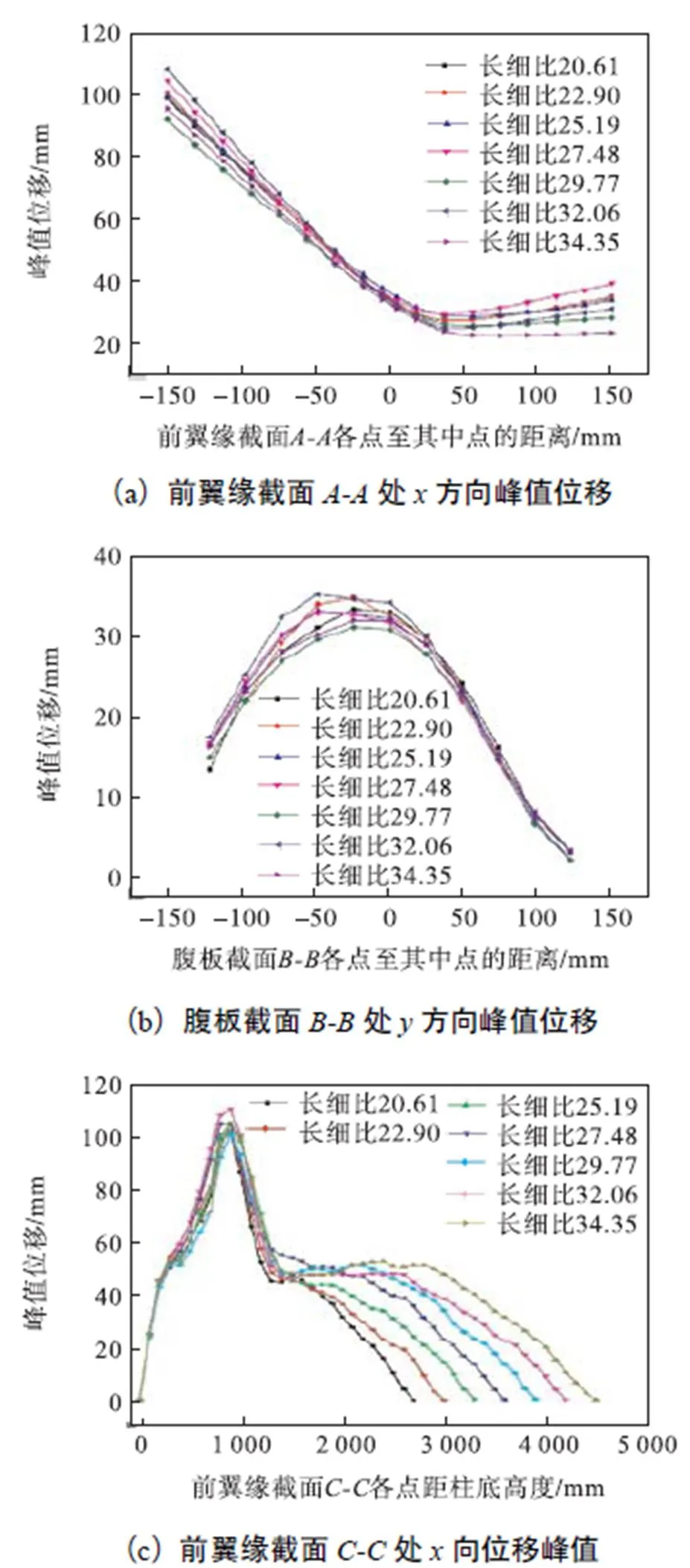
图17 不同柱高下钢柱前翼缘和腹板峰值位移

4.3 钢材强度

钢材强度是钢柱竖向承载力的重要影响因素.为探究在汽车撞击与爆炸复合作用下钢材强度对钢柱损伤效应的影响．保持钢柱截面类型和尺寸完全相同，柱高均为3m，为更明显体现不同钢材强度的钢柱的变形差异，轴向压力取0.4p＝3200kN．本节分别模拟了钢材强度为Q235、Q345、Q390、Q420和Q460这5种情况下的钢柱损伤模型．

由图18可知，H型钢柱截面处和处向峰值位移和截面处向峰值位移当钢材强度由Q235提高到Q345，H型钢柱该3项峰值位移均大幅减小．而Q345、Q390、Q420、Q460等钢材强度的截面处、处和处的峰值位移均较为接近，随着钢材强度的增大，峰值位移的增幅较小．从上述分析可知，H型钢柱在汽车撞击与爆炸复合作用下，如果原先选用的钢材强度较小，峰值位移较大，适当提高强度能有效减小位移幅值．但由于低强度钢材的应变率效应更为敏感[12]，故一味地提高钢材强度并不能达到持续有效地减小变形幅值的效果.因此，在钢柱抗冲撞抗爆设计中，为提高钢柱抗汽车撞击与爆炸复合作用的能力，若原选用钢材强度较小，可适当提高钢柱钢材的强度，但不能盲目提高钢材强度．

图18 不同钢材强度下钢柱前翼缘和腹板峰值位移

4.4 截面类型

为探究不同的截面类型对钢柱的抗汽车撞击与爆炸复合作用能力的影响，在保持钢柱高度相同、截面面积相同，即总用钢量相同的情况下，本节选取H型钢柱、方形空心型钢柱和圆形空心型钢柱进行数值模拟分析．钢材强度均为Q390，轴压比为0.4，即轴向压力为3200kN，柱高均为3m．

图19是不同截面类型钢柱在汽车撞击与爆炸复合作用下的塑性应变云图对比．由图中可知：H型钢柱迎爆面有明显的塑性变形，且前翼缘表面有一定的撞击凹陷和局部屈曲变形．H型钢柱背爆面局部区域也有较明显的塑性变形．方形空心型钢柱迎爆面有较为严重的塑性变形，且表面有明显的撞击凹痕和较大区域的屈曲变形．方形空心型钢柱背爆面与侧爆面也发生较明显的塑性变形且局部发生屈曲．圆形空心型钢柱迎爆面仅在柱底局部有较明显的塑性变形，且柱身并无明显撞击凹陷．圆形空心型钢柱背爆面几乎没有明显的塑性变形．

图19 不同截面类型钢柱塑性应变云图对比

图20为不同截面类型钢柱中点(位置参见图19)方向位移时程曲线．由图可知，圆形空心型钢柱点水平向残余位移最小，H型钢柱水平向残余位移较小，方形空心型钢柱发生了很大的水平位移，且水平位移增长速度明显大于H型和圆形空心型钢柱．虽然最后水平位移部分回弹，但最后很快就趋于稳定，说明方形空心型钢柱发生的位移大部分是属于塑性变形．

图21为柱顶节点(位置参见图1)的方向(竖向)峰值位移时程曲线，由图可知，圆形空心型截面与H型截面钢柱柱顶节点的竖向位移均较小，且竖向位移经过部分回弹后趋于平稳，说明两者并未发生屈曲失稳破坏．方形空心型截面钢柱柱顶节点竖向位移一直保持增长，且并无稳定趋势，说明其已经发生屈曲失稳破坏．

图20 柱中A点x方向峰值位移时程曲线

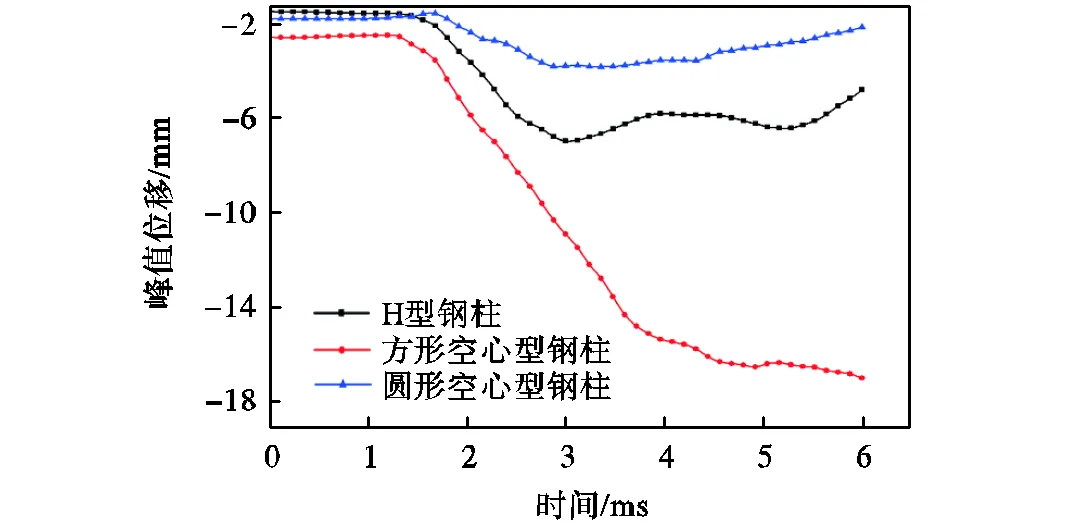
图21 柱顶B点z方向峰值位移时程曲线

5 结 论

(1) 汽车撞击是局部冲击荷载，局部破坏较为明显，整体损伤相对较小；爆炸波是球面型冲击波，在近爆情况下，钢柱整体损伤较大，全局损伤分布较为均匀，局部破坏间差异较小．

(2) 在汽车撞击与爆炸荷载复合作用下，钢柱首先受到汽车的撞击作用，而由于炸药起爆点位于汽车中后方，爆炸冲击波传播过程中将会与汽车发生相互作用；汽车在爆炸波的冲击作用下发生较大的破坏，且消耗部分爆炸波能量；爆炸冲击波会因汽车的阻挡作用发生反射和绕流现象，导致钢柱因爆炸产生的动力响应减弱．因此汽车对于爆炸冲击波传播的影响效应很大．

(3) 考虑到因车底一侧有大体积油箱导致汽车质心偏离其几何中心，碰撞过程中汽车偏转致使前翼缘两侧峰值位移较不均匀，质心偏移一侧前翼缘峰值位移明显高于另一侧，且峰值位移整体相对较小；爆炸冲击产生的前翼缘两侧变形位移比较对称，整体峰值位移相对较大．

(4) 为保证H型钢柱的抗冲撞与抗爆性能，应限制其轴向压力值，若钢材强度选用Q390，则轴压比宜控制在0.4以内；若原选用的钢材强度较小，适当提高钢材强度可达到提升钢柱抗冲撞与抗爆性能的效果，但不能盲目提高钢材强度；改变长细比对钢柱的抗冲撞与抗爆性能整体影响较小；在保持钢柱的高度与用钢量一致的前提下，圆形空心型截面钢柱的抗冲撞与抗爆性能最优，H型截面钢柱次之，方形空心型截面钢柱最差且与前两者差距较大．

［1］ 尹 越，黄逸群，王秀泉. 车辆撞击钢结构人行天桥有限元分析[J]. 天津大学学报：自然科学与工程技术版，2016，49(增1)：129-136.

Yin Yue，Huang Yiqun，Wang Xiuquan. Finite element analysis of steel pedestrian bridges under vehicle collision[J]. Journal of Tianjin University：Science and Technology，2016，49(Suppl1)：129-136(in Chinese).

［2］ 丁 阳，宋骁然，师燕超. 爆炸荷载作用下基于抗剪承载力的钢柱失效准则[J]. 北京工业大学学报，2014，40(8)：1151-1155，1162.

Ding Yang，Song Xiaoran，Shi Yanchao. Failure criterion of cteel columns cnder blast load based on maximum shear resistance[J]. Journal of Beijing University of Technology，2014，40(8)：1151-1155，1162(in Chinese).

［3］ 李月强，衣 娜，席 丰. 钢柱抗爆响应分析单自由度模型适用性评估[J]. 爆炸与冲击，2017，37(5)：957-963.

Li Yueqiang，Yi Na，Xi Feng. Assessment on single degree of freedom model in steel column analysis of anti-detonation[J]. Explosion and Shock Waves，2017，37(5)：957-963(in Chinese).

［4］ 张秀华，张春巍，段忠东. 爆炸荷载作用下钢框架柱冲击响应与破坏模式的数值模拟[J]. 沈阳建筑大学学报：自然科学版，2009，25(4)：656-662.

Zhang Xiuhua，Zhang Chunwei，Duan Zhongdong. Numerical simulation on impact responses and failure modes of steel frame structural columns subject to blast loads[J]. Journal of Shenyang Jianzhu University：Natural Science，2009，25(4)：656-662(in Chinese).

［5］ 杨涛春，陆 勇，李国强，等. 工字形钢柱的爆炸作用分布特征与计算研究[J]. 振动与冲击，2016，35(5)：27-38.

Yang Taochun，Lu Yong，Li Guoqiang，et al. Distribution features and calculation of blast loading for I-shaped steel columns subjected to explosion[J]. Journal of Vibration and Shock，2016，35(5)：27-38(in Chinese).

［6］ GB/T 11263—2010 热轧H型钢和剖分T型钢[S]. 北京：中国标准出版社，2010.

GB/T 11263—2010 Hot-Rolled H and Cut T Section Steel[S]. Beijing：China Standard Press，2010(in Chinese).

［7］ 师燕超. 爆炸荷载作用下钢筋混凝土结构的动态响应行为与损伤破坏机理[D]. 天津：天津大学，2008.

Shi Yanchao. Dynamic Response Behavior and Damage Mechanism of Reinforced Concrete Structures Under Explosive Load[D]. Tianjin：Tianjin University，2008(in Chinese).

［8］ 余 敏. 不同类型柱子在汽车撞击作用下的性能研究[D]. 哈尔滨：哈尔滨工业大学，2007.

Yu Min. Research on the Capability of Different Types of Columns Crashed by Different Types of Cars[D]. Harbin：Harbin Institute of Technology，2007(in Chinese).

［9］ Chung K Y S，Langdon G S，Nurick G N，et al. Response of V-shape plates to localized blast load experiments and numerical simulation[J]. International Journal of Impact Engineering，2012，46：97-109.

［10］ 崔娟玲，郭昭胜，王 蕊，等. 热轧H型钢柱侧向冲击试验研究[J]. 振动与冲击，2014，33(18)：133-139.

Cui Juanling，Guo Zhaosheng，Wang Rui，et al. Tests for behavior of a hot rolled H-shaped steel column under lateral impact[J]. Journal of Vibration and Shock，2014，33(18)：133-139(in Chinese).

［11］ Nassr A A，Razaqpur A G，Tait M J，et al. Dynamic response of steel columns subjected to blast loading[J]. Journal of Structural Engineering，2014，140(7)：04014036.

［12］ 林 峰，顾祥林，匡昕昕，等．高应变率下建筑钢筋的本构模型[J]. 建筑材料学报，2008，11(1)：14-20.

Lin Feng，Gu Xianglin，Kuang Xinxin，et al. Constitutive models for reinforcing steel bars under high strain rates[J]. Journal of Building Materials，2008，11(1)：14-20(in Chinese).

Damage Effect Analysis of H-Section Steel Columns Subjected to Synergistic Effects of Vehicle Impact and Blast

Tian Li1, 2，Mao Zujie1

(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China； 2. Key Laboratory of Coast Civil Structure Safty of Ministry of Education(Tianjin University)，Tianjin 300072，China)

To investigate the anti-knock and anti-blast performance of H-section steel column under the synergistic effect of vehicle impact and blast，using the finite element software for nonlinear analysis ANSYS/LS-DYNA，the damage effect of the combined vehicle impact and blast loads on the H-section steel column is simulated by establishing the whole process model of vehicle explosion after striking a steel column. The difference of dynamic response of H-section steel columns under three working conditions，i.e. vehicle impact，blast load，and combined impact and blast load，are compared and analyzed. Meanwhile，the influences of the axial compression ratio，slenderness ratio，steel strength，and cross section type on the damage effect of H-section steel column under the combined impact and blast load are investigated by parametric analysis method. The results show that the vehicle impact deflection causes significant difference in displacement on both sides of the front flange，and the side of the center of mass deviation is obviously higher than the other side. The displacement on both sides of the front flange is symmetrical due to explosion impact，and the overall displacement is relatively large. The shock wave is reflected and flows by the blocking action of the vehicle，so that the dynamic response of the steel column due to the explosion is weakened. To ensure anti-knock and anti-blast performance of the H-section steel column，the axial pressure value of the steel column should be limited；when the steel strength grade is Q390，the axial pressure ratio should be controlled within 0.4. A reasonable steel strength should be chosen for steel column；if the strength of the original steel is small，properly increasing the steel strength can improve the anti-knock and anti-blast performance，but cannot blindly increase the steel strength. Changing slenderness ratio has less impact on the anti-knock and anti-blast performances of steel column. Under the premise of keeping the column height consistent with the total steel consumption，the circular hollow section steel column has the best anti-knock and anti-blast performance，followed by the H-section steel column，and the square hollow section steel column has the worst performance，which has a big gap from that of the former two. The research results in this paper can provide a theoretical basis for further research on the anti-impact and anti-knock protection measures of steel columns.

vehicle impact；blast；synergistic effects；steel column；damage effect

10.11784/tdxbz201807007

TU318

A

0493-2137(2019)07-0709-10

2018-07-04；

2018-11-25.

田 力（1970—  ），男，博士，副教授.

田 力，ltian@tju.edu.cn.

国家自然科学基金重点资助项目(51238007，51178310).

the Key Program of the National Natural Science Foundation of China(No.51238007，No.51178310).

(责任编辑：樊素英)