压水堆核电站蒸汽发生器二次侧两相流流场特性模拟

刘丽艳，苏 桐，郭 凯，王一鹏，熊光明, ，朱 勇，谭 蔚，唐国武



压水堆核电站蒸汽发生器二次侧两相流流场特性模拟

刘丽艳1，苏 桐1，郭 凯1，王一鹏1，熊光明1, 2，朱 勇2，谭 蔚1，唐国武3

(1. 天津大学化工学院，天津 300350；2. 中广核工程有限公司，深圳 518124；3. 山东师范大学化学化工与材料科学学院，济南 250014)

压水堆核电站蒸汽发生器中二次侧流体流过传热管束会使管束发生振动，可能造成管束损坏，引发事故．蒸汽发生器尺寸较大，内部结构复杂，难以进行全尺寸实验，数值模拟方法是研究蒸汽发生器热工水力特性的常用方法．现有研究以设计工况下的热工水力参数为主，而对于不同冷热端给水比条件、或存在防振条偏移时传热管上流体力的分布规律考虑不足．为分析流场状态与流体力分布规律，使用FLUENT软件及多孔介质模型研究蒸汽发生器二次侧流场特性，通过分布式阻力表征流域内管束、支撑板、防振条等组件的影响，将一次侧对二次侧热交换能量以边界条件形式加入到模型中，基于零方程湍流模型，并结合两相漂移流模型计算得到了流场的温度、空泡率、速度、横流动能的分布规律，同时研究了冷热端给水比与防振条偏移对流体力分布的影响．结果表明：在设计工况下，轴向高度3m时二次侧流体均升温至沸点并保持稳定，空泡率随换热过程的进行而逐渐增加，在二次侧出口处平均值为90%；流体速度与空泡率、流动方向及流场结构有关，热端平均流速呈现在直管段增加、弯管段降低的趋势，在8.8m高度达到最大值5.36m/s，而冷端流速在轴向高度2.2m前略有降低，随后与热端趋势相同，8.8m高度处为最大值3.56m/s；流体对管束的作用在二次侧入口区域与弯管区域较明显，而在直管段几乎没有影响；冷热端给水比例的变化仅对入口处流体动能分布影响较大；防振条偏移会对局部流体力分布造成影响，两组防振条之间流速和动能将平滑变化．

蒸汽发生器；热工水力；数值模拟；两相流

蒸汽发生器作为压水堆核电站一、二次侧回路的换热枢纽，其中包含的大量传热管也是核岛一次侧回路中最为薄弱的部分．据统计，由蒸汽发生器失效造成核电机组计划外停堆的比例占所有意外事故的25%，而多数蒸汽发生器的失效原因是传热管破损[1].这些传热管壁厚仅为1mm左右，因处于高温高压、高速流体冲刷的极端工况环境，虽然已经采用特殊标准的镍基合金材料，但仍易因腐蚀、振动、磨损等因素造成传热管破损，导致一次侧含辐射流体泄漏[2-4].由于传热管的失效与二次侧流动状态密切相关，故研究二次侧热工水力特性和流场参数，有助于研究蒸汽发生器失效机理，对指导蒸汽发生器的设计和安全运行具有重要意义．

由于蒸汽发生器尺寸较大，内部结构复杂，难以对其进行全尺寸实验．随着计算流体动力学(CFD)的发展，数值模拟方法已成为研究蒸汽发生器热工水力特性的常用方法．面对蒸汽发生器复杂的内部结构，对每一个内部组件进行建模并绘制网格所需的计算资源过于巨大，采用多孔介质模型表征各组件造成的压力损失几乎是目前唯一的模拟手段[5-6]．Patankar等[7-8]首先验证了多孔介质方法的有效性并分析了换热器壳程流场特性．Lu等[9]基于双流体模型开发了THAC-SG热工水力分析代码，并通过大亚湾核电站蒸汽发生器的参数对代码进行了验证．Hovi等[10]将APROS专用软件的计算结果作为一次侧流场边界，从而建立二次侧流场的CFD模型，研究了二次侧在压力变化过程中流场特性的变化．Cong等[11-12]等提出双层网格模型耦合一、二次侧流场的方法，并利用该方法对二次侧流场进行了分析．

目前对于蒸汽发生器二次侧流场的分析，以研究设计工况下的基本热工水力参数为主，但此类参数无法直接用于传热管振动计算．此外，二次侧给水受给水环管影响，其冷热端给水量可能不一致，造成流场状态变化．同时流体对管的作用力(以下简称流体力)分布对传热管振动有直接影响，但尚鲜见研究说明防振条偏移对于传热管上流体分布的影响．本文基于多孔介质方法研究了蒸汽发生器二次侧流场的热工水力特性，同时分析了不同区域流体横向流过管束的流体动能密度，考虑了冷热端给水比例的影响，并对可能发生的防振条偏移进行了分析．

1 数学模型与计算方法

1.1 数学模型

在蒸汽发生器中，流体以过冷状态进入二次侧流场，以高空泡率状态离开流场进入汽水分离器，考虑到其中的两相流状态与流动的不均匀性，本文采用两相漂移流模型[13-14]，其控制方程为

 (1)

   (2)

   (3)

在两相漂移流模型中，相间滑移速度定义为

 (4)

研究中一次侧与二次侧的热交换能量以边界条件的形式加入到模型中，单位体积内使液相沸腾的能量为

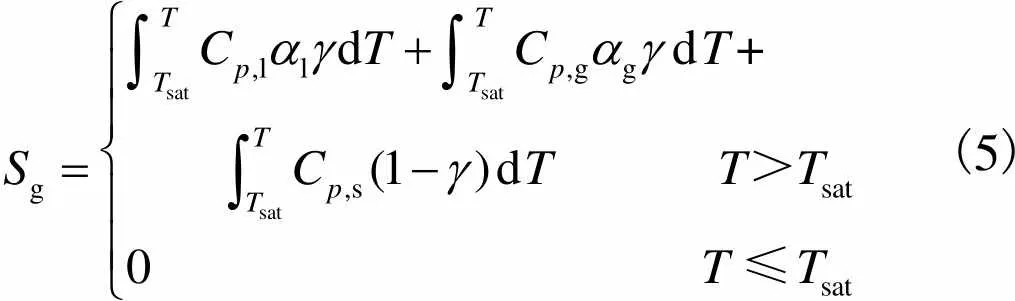
 (5)

采用零方程湍流模型[15-16]计算湍流黏性，有效黏性的定义为

 (6)

模型依靠多孔介质表征二次侧流场内的部件对流体的影响，针对管束、支撑板、防振条等不同区域位置，利用用户定义函数(UDF)确定每个位置上不同方向的阻力系数，其压力损失的计算式为

 (7)

1.2 物理模型与边界条件

本文的计算模型根据实际自然循环蒸汽发生器的结构建模得到，图1为蒸汽发生器的结构示意．建模区域为二次侧流场从下部管板上表面到上部汽水分离器之间的范围，其中包含全部换热管束、防振条与支撑板，均采用多孔介质方法进行建模分析．模型中5组防振条均布于弯管区域，9块支撑板间距相等，为传热管束起到支撑作用．由于模型的对称性，建模范围为1/2整体模型．

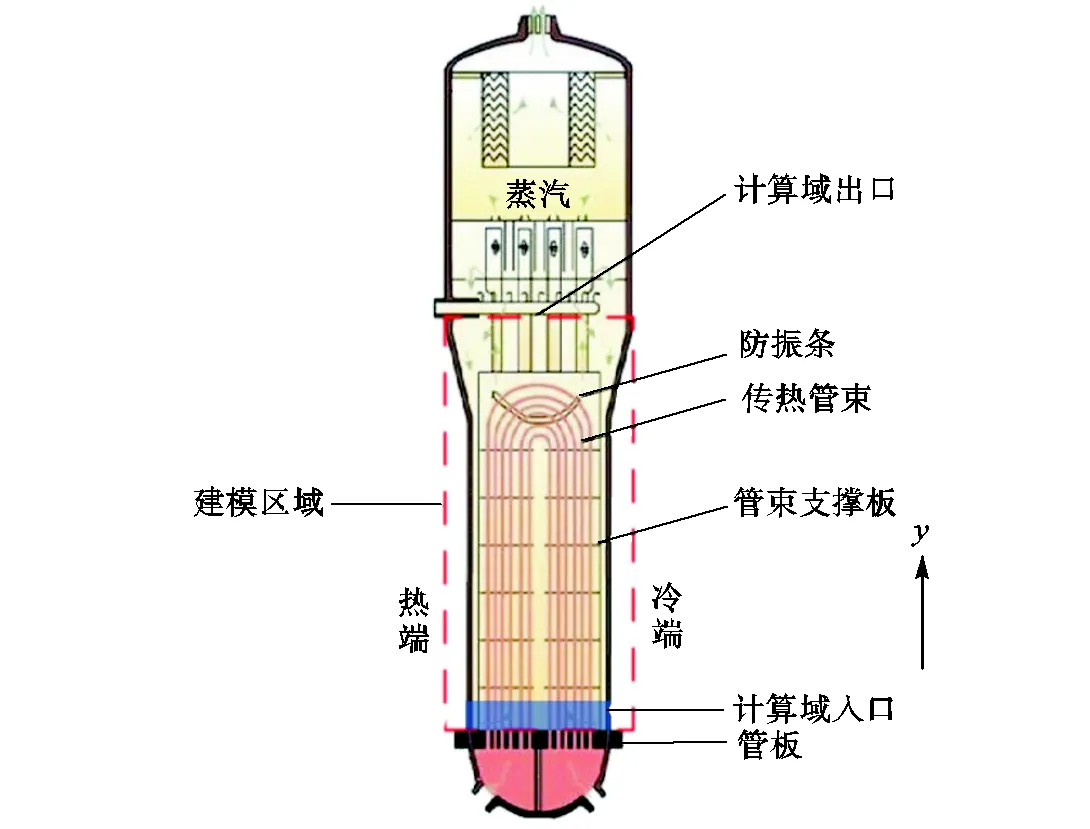
图1 模型区域示意

模型以管板上表面为轴基准面，二次侧流体从管板与管束套筒的间隙水平进入计算域，其轴向高度范围为0～0.36m，该边界设置为速度入口边界条件，速度分布表达式为

 (8)

管束套筒顶部为压力出口边界条件；管板上表面以及管束套筒的外缘为无滑移壁面边界条件；1/2模型的分割面为对称边界条件．

2 网格划分及模型验证

如图2所示，模型采用ICEM 软件划分结构网格，其最低网格质量高于0.75．为保证计算结果的准确性，在研究前进行了网格无关性检验，分别得到网格数量为704488、1512240、2107970的模型，同时取蒸汽发生器专用软件的计算结果进行对比．表1为本文模型与专用软件结果的相对误差值，可以看出，专用软件的计算结果与Fluent的结果几乎一致，且对于本文所选择的网格数量范围，计算结果变化较小．后续研究选用了1512240网格的计算模型．

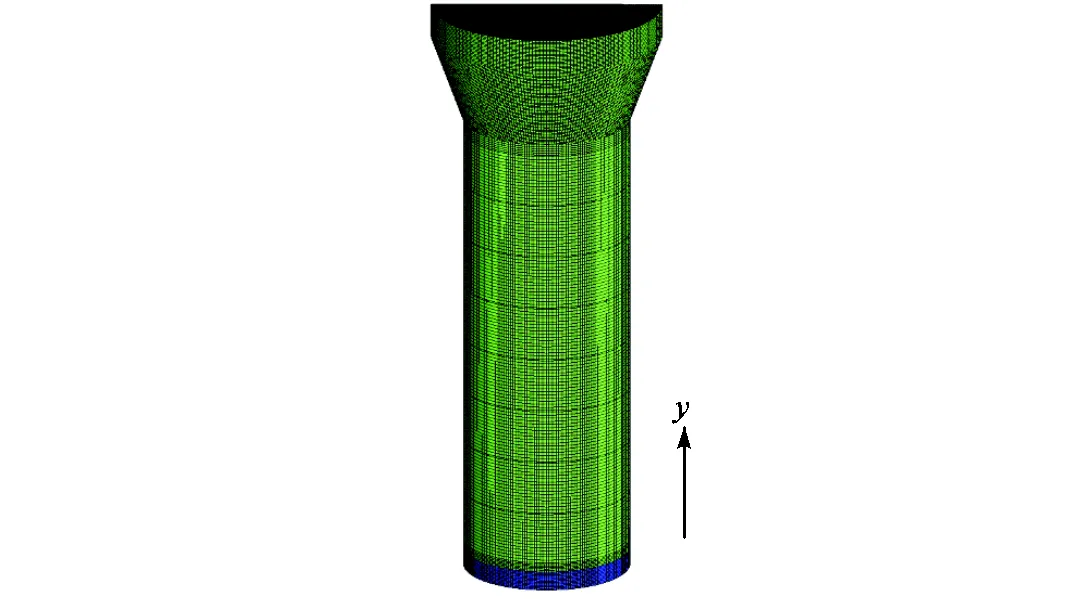
图2 网格划分

表1 结果对比与网格无关性验证

Tab.1 Comparison results and grid independence check

3 结果与讨论

基于以上理论模型，本文先研究了设计工况下二次侧流场的热工水力特性和流体横流过管束的能量分布状况，随后依次研究了冷热端给水比例、防振条偏移对流体横流动能分布的影响．

3.1 蒸汽发生器二次侧流场特征分析

图3和图4分别为对称面温度分布和流场沿轴向的温度曲线．流体进入流场为过冷状态，温度为542.7K．随着热交换过程的进行，二次侧流体温度随轴向高度不断上升，直至达到沸点．在沿轴向的0.4m高度内，由于入口流量随高度增加而增加，截面温度上升缓慢、冷端最高温度略有下降．图4中温度最大值达到沸点表明相变开始，而最小值达到沸点则表明相变从过冷沸腾彻底转换为饱和沸腾．热端的最高温度始终为沸点，说明管板上表面处已经有汽相产生，而冷端在轴向高度1.8m左右才开始发生相变．热端从轴向高度0.4m到1.4m平均温度上升了5.4K，而从1.4m到2.4m平均温度仅上升了0.7K，这是由于低于1.4m高度时一次侧向二次侧传递的热量主要用于加热过冷液体，而1.4m后热量更多地用于液体沸腾，此时饱和沸腾开始占主导地位．而在冷端传热功率较低，流体温度相对均匀，在轴向高度2.8m时升温速度仍没有明显下降．在3m高度时，所有位置均达到沸点且温度保持稳定，过冷沸腾过程彻底结束．

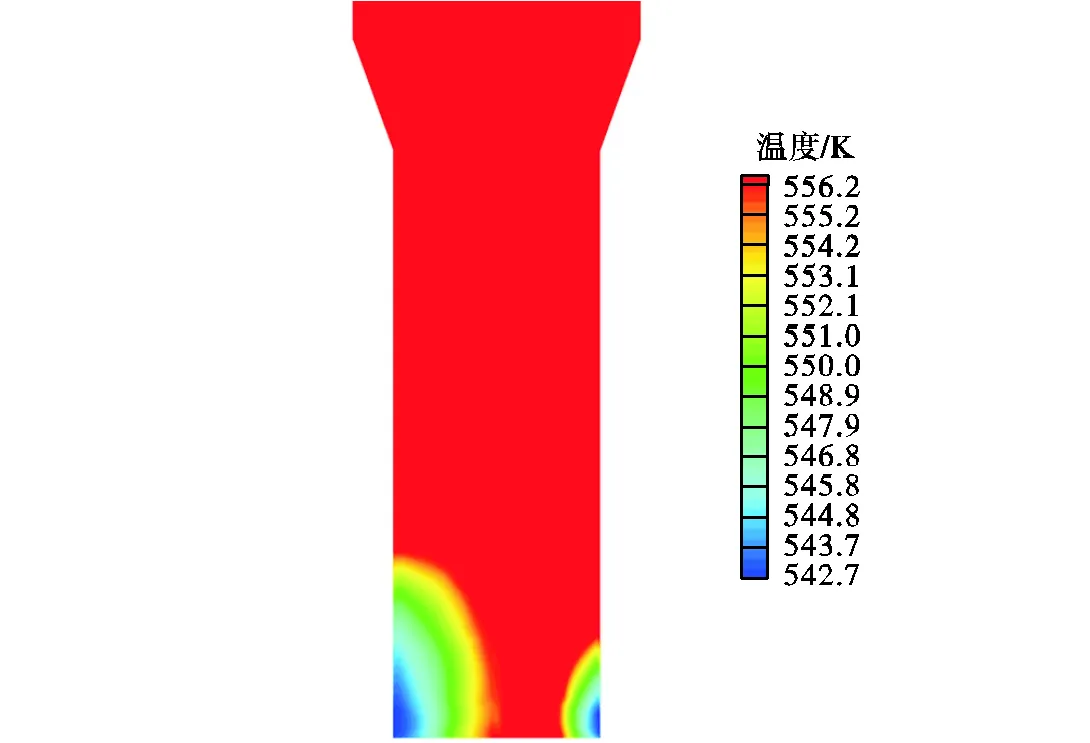
图3 对称面温度分布

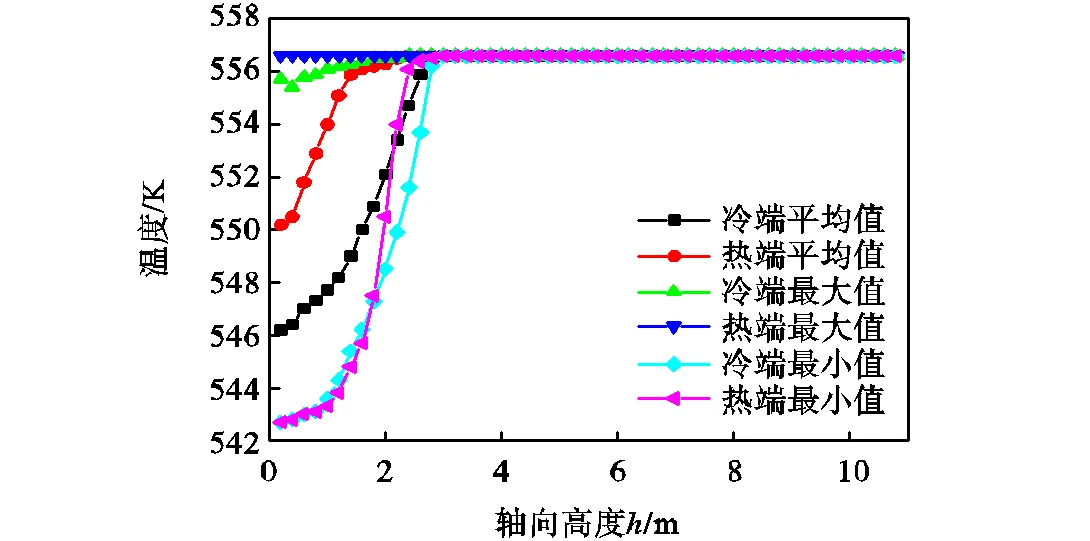
图4 轴向流场温度分布曲线

在蒸汽发生器中，二次侧流体从单液相到高汽相分率的汽液两相环状流状态，状态变化复杂[17]，本研究以空泡率的变化情况表征流体两相流动状态的变化，如图5和图6所示．热端在管板上表面的平均空泡率约为9%，并随高度逐渐增加，而冷端流体从入口处到2m高度范围内，平均空泡率几乎为0，与温度分布规律相同．冷热端间的空泡率差值从入口开始逐渐增加，在2.2m高度处达到最大50%，随后由于冷端进入沸腾，同时冷热端流体混合，空泡率差值逐渐减低，到上部出口附近时降至7%，同时出口处总平均空泡率为90%．

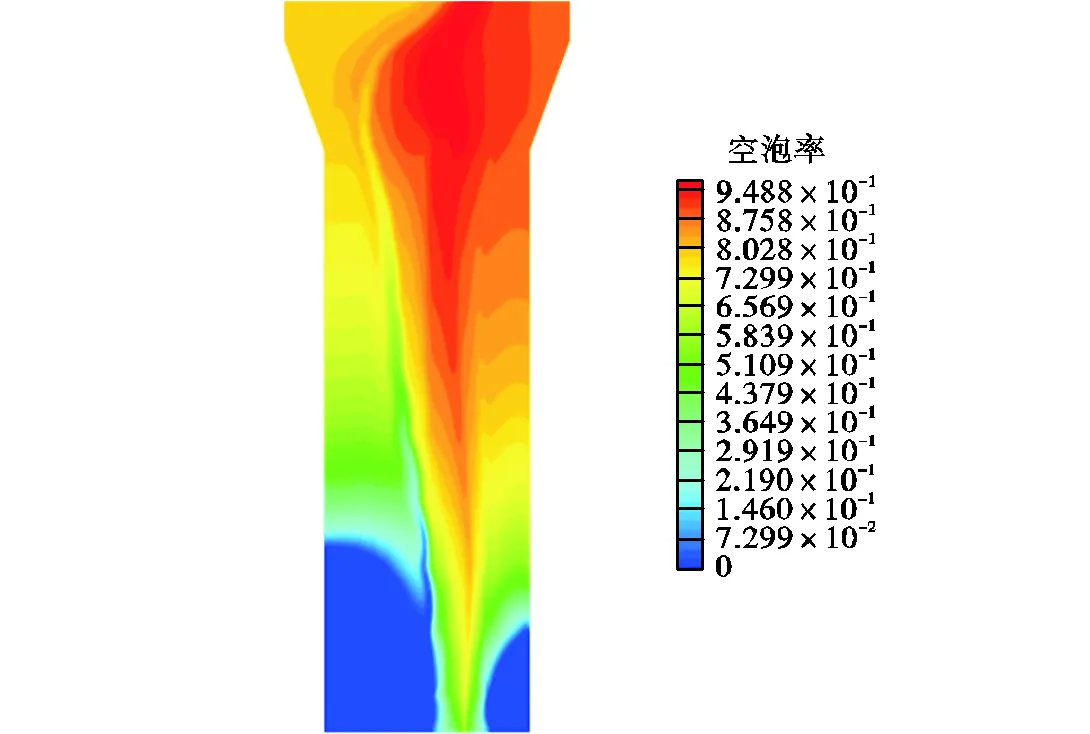
图5 对称面空泡率分布

图6 轴向流场空泡率分布曲线

流场速度的分布情况如图7和图8所示．在直管段，由于空泡率提升，热端平均流速随高度逐渐增加，在8.8m高度时达到最大值5.36m/s．而冷端平均速度随高度增加而先逐渐降低，轴向高度2.2m时达到最低值0.38m/s，而后又随之增加，8.8m高度时为3.65m/s．这是由于低于2.2m高度时，冷端流体接近单相液体，其流动方向从进入流场的径向转变为轴向，造成了流速下降，而2.2m高度后冷端空泡率大幅提升，提高了冷端的体积流率．到达U型弯管区域时，由于扩张段的结构设计，面平均流速随截面积的增加而减小，在出口处降至1.56m/s．由于同一高度上热端空泡率比冷端更高，体积流率相应较高．在9m高度左右的位置，最大流速急剧增加，这是由于在扩张段上少量流体在管束区外部产生了壁流现象.

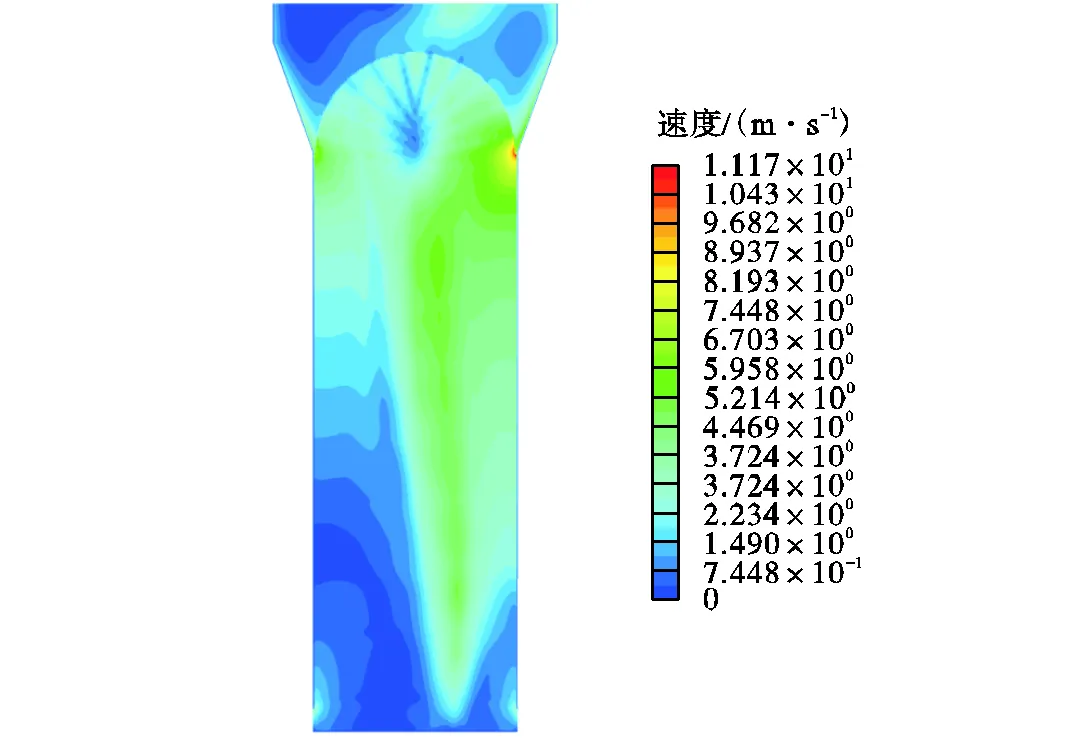
图7 对称面速度分布

图8 轴向流场速度分布曲线

在蒸汽发生器中，管束的振动主要由于流体横流冲刷管束导致，其振动状态与管束自身结构、流体密度、速度分布密切相关．

图9和图10分别展示了最外侧弯管区域与流场沿管束方向的横流速度分布，图10中横坐标为管束中沿最外侧传热管的轴线长度．可以看出，弯管区域横流速度最高，最大速度在45°与135°附近位置，而平均流速较为稳定，冷端平均流速约为热端的80%，同时防振条对流动有明显阻碍，各组防振条附近流速较低．在直管段，二次侧流体入口横流速度较高，最大流速接近4m/s，同时由于支撑板的阻碍作用，流体在流过支撑板前横流速度逐渐上升，并在流过支撑板后降至几乎为零．

图9 传热管弯管区外表面横流速度分布

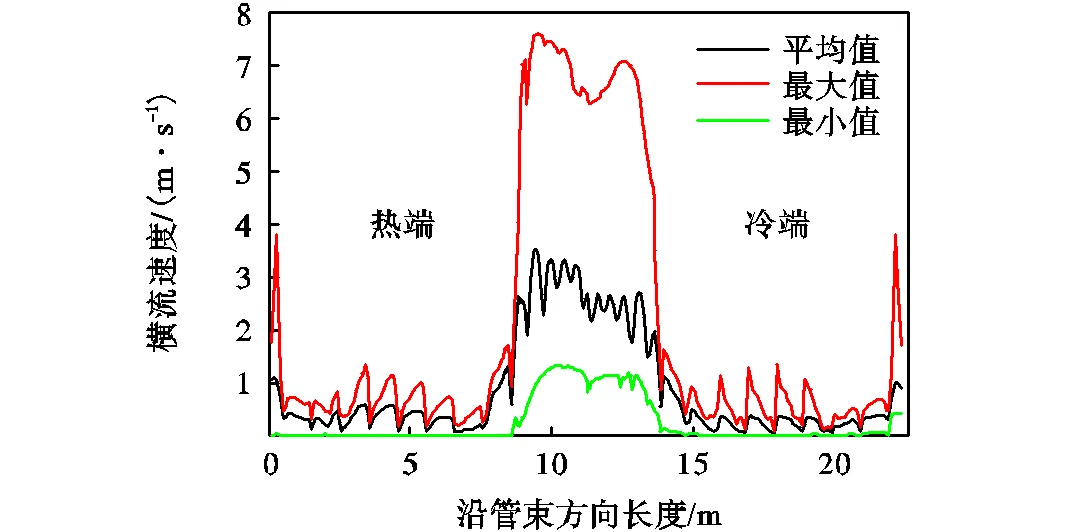
图10 沿管束方向横流速度分布

流体动能密度定义为

 (9)

其值体现了传热管受流体作用力的大小．

图11和图12是弯管区域与流场沿管束方向的流体横流流体动能密度分布，可以看出在入口区域流动以横流为主，由于流体密度最大，最大横流流体动能密度超过5500J/m3，对管束冲击能量很高．直管区流动以轴流为主，横流能量不到入口区域的10%．在弯管区域第1组防振条范围内流体动能密度较低，这是因为此处空泡率很高，流体密度低，造成流体总动能并不高，而从第1组防振条到第5组防振条之间平均流体动能密度逐渐上升，而最大流体动能密度与流速趋势相同，在45°和135°左右达到最大值约3900J/m3，且热端略高于冷端．

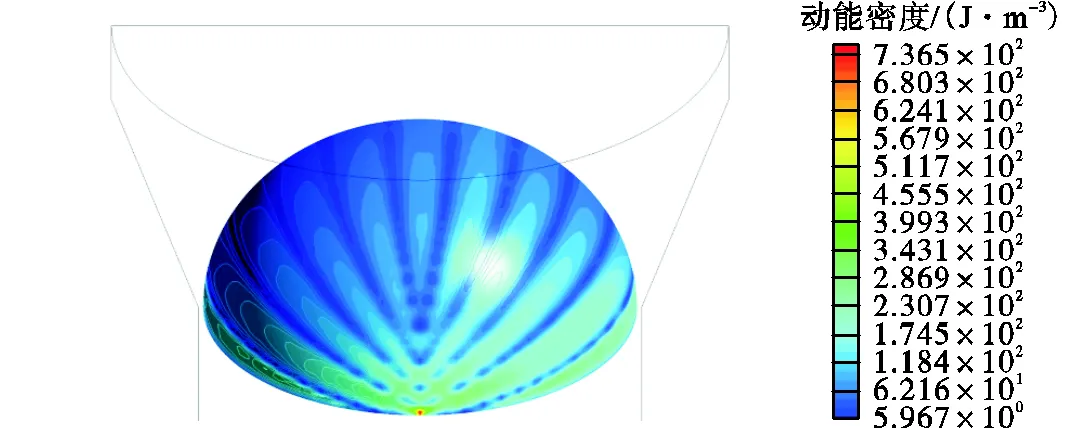
图11 传热管弯管区外表面横流流体动能密度分布

图12 沿管束方向横流流体动能密度分布

综合考虑传热管的结构刚度与流体流动分布情况，取对称面上半径最大的传热管R114号管(见图13)作为研究对象，得到沿管的横流速度、流体密度与横流流体动能密度分布，如图14所示．在二次侧入口处，其横流流体动能密度最高，由于此时流体处于过冷状态，其流体动能密度几乎只与流速相关，对于该处的振动校核可按照单相流体进行．在直管段流体沿轴向运动，流动对管束振动影响很小．在弯管区域，冷端流体密度相对高于热端，但流速较低，总体流体动能密度低于热端．

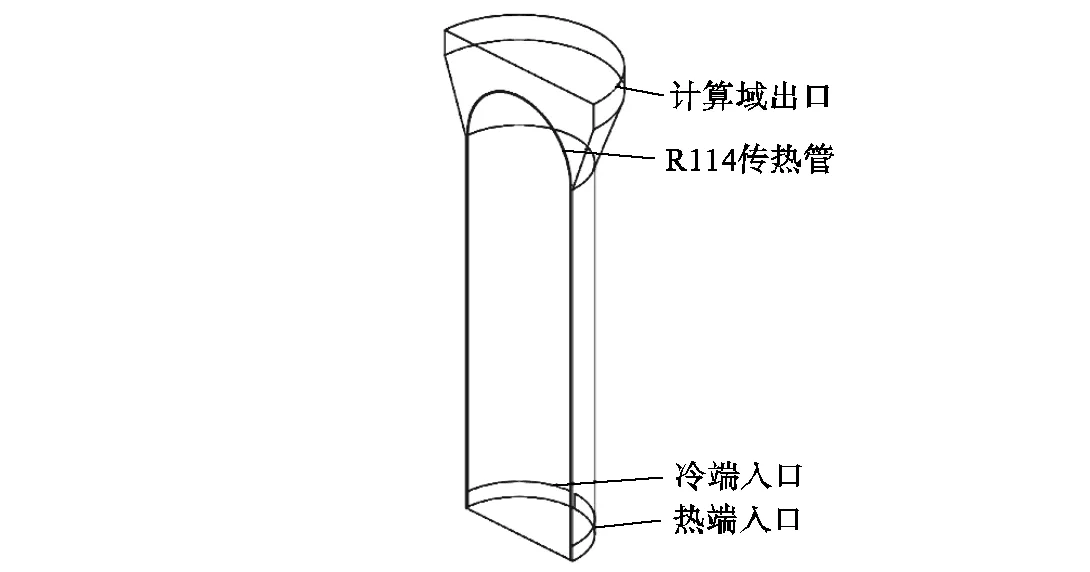
图13 R114号传热管示意

图14 R114号传热管流体特性分布

3.2 冷热端给水比对流体动能分布的影响

针对冷热端不同的给水比例，本节主要考虑流体对传热管作用的能量分布情况，分别考虑冷热端给水比为1∶3、2∶3、1∶1、3∶2、3∶1的条件，并以R114号管为例进行单管的详细分析．

分别获得二次侧流场沿一次侧流动方向的平均横流速度、平均流体密度和平均横流流体动能密度，如图15～图17所示．在二次侧入口位置，由于相变作用较弱，流体密度接近单相液体，其流体动能密度只与流速相关，不平衡的给水比会造成单侧管束受流体作用力过大，冷热端给水比为3∶1时的平均流体动能密度是1∶1时的2倍．在直管段，提高冷/热端给水比会降低冷端空泡率，从而提高冷热端之间的体积流量差，使横流速度有所提高．不同给水比状态下，流体密度变化总趋势相同，但提高单侧给水量可以略微减缓直管段流体密度下降的速度．随着轴向高度增加，流体由于湍流和横流作用逐渐混合，到弯管区域时流体密度与横流流速变化很小，由图18可以看出，不同条件下弯管区域的流体动能分布基本一致.

图15 沿管束方向平均横流速度分布

图16 沿管束方向平均流体密度分布

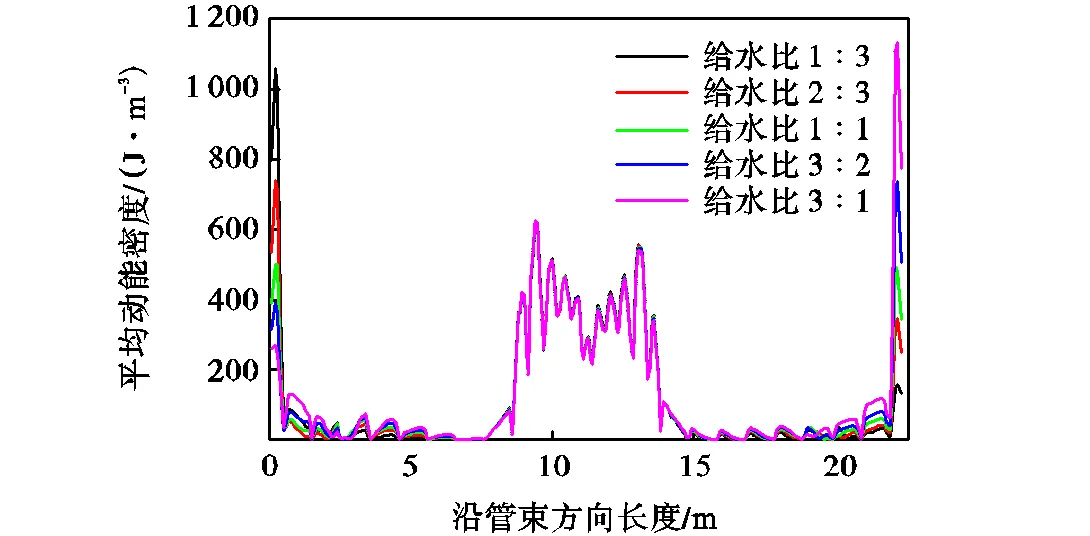
图17 沿管束方向平均横流流体动能密度分布

图18 不同给水比下R114号传热管流体特性分布

如图18所示，沿R114号管上的流体状态与二次侧流场的平均分布趋势相同，冷热端给水比的影响主要位于蒸汽发生器二次侧的入口处．对于管束直管段，随着单侧流量增加，沸腾起始点相对滞后，从而提高了截面上的流体密度，其主要影响轴向高度1～5m范围，但由于直管段横流速度很低，平均横流动能密度低于10J/m3，对管束振动不会产生明显影响．在弯管区域，流体混合相对充分，给水比对流体密度和速度分布均影响较小．由于选取的是振动分析时最具代表性的传热管，其受到的流体作用远高于平均值，如入口处最大流体动能密度接近10000J/m3，是平均值的9倍，故对于传热管的振动校核，在工程计算时应该对所有关注的传热管分别提取流体力并作校核．

3.3 防振条偏移的影响

蒸汽发生器传热管防振条的位置偏移会改变流场结构与流体能量分布，可能造成管束局部振动．本文仍取R114号传热管进行分析，对夹持R114号传热管的防振条分别进行偏移，并得到弯管区域的流体分布状态．

图19～图22为夹持R114号管的每组防振条分别向两端偏移后，弯管区域内沿管束的流体横流速度、流体密度以及流体动能密度分布情况，其中防振条1和防振条2偏移20°，防振条3和防振条4偏移15°．图中黑线为未发生防振条偏移的对照组，红线为防振条向冷端偏移，蓝线为防振条向热端偏移．

参考对照组可知，由于防振条对流动存在阻碍作用，整个弯管段被5组防振条分成了11跨，每一跨间流速远高于防振条附近流速．由于流动倾向于穿过较少数量的防振条，故两侧流速较高，最大可达5.8m/s．在弯管角度70°～100°之间流体流量相对较低，但空泡率最高，流速超过4m/s．流体密度分布从冷端到热端呈现先降低后升高的趋势，冷端流体密度最大，90°位置最小．弯管区域两侧流体动能密度高于其他位置，且热端高于冷端，此外90°位置受高横流流速影响，流体动能密度约500J/m3．

图19 防振条1偏移时流体特性分布

图20 防振条2偏移时流体特性分布

图21 防振条3偏移时流体特性分布

图22 防振条4偏移时流体特性分布

对比各组结果可以发现，防振条偏移对流体密度分布的影响较小，但对其附近区域流速有一定影响．在防振条偏移超过初始角度后，任意两组防振条之间的流体流速会保持平滑变化，且不会超过该段区域原本的最大流速．由于流体密度变化受防振条影响很小，故其横流流体动能密度的变化趋势与流速变化相关．这表明在防振条偏移后，管上任意位置的流体力也会平滑变化，且小于偏移前最近两跨间的流体力峰值．

4 结 论

本文基于多孔介质方法建立了压水堆核电站蒸汽发生器二次侧流场的计算模型，通过分布阻力方式表征了蒸汽发生器中内部组件的影响，得到了二次侧流场的热工水力特性，并着重研究了传热管受流体力作用的变化规律，得出以下结论．

(1) 流体对管束振动的作用与流体密度和横流速度相关，在入口与弯管区域流体横流动能较高，最大横流流体动能密度超过5500J/m3，而在直管段流体动能密度不到入口区域的10%．

(2) 冷热端给水比的变化直接影响入口处管束受流体的作用力，不平衡的给水比会显著增大入口局部传热管附近的流体动能密度，冷热端给水比为3∶1时平均流体动能密度是1∶1时的2倍，而在弯管区域流体的状态分布受冷热端给水比的影响较小．

(3) 流体密度受防振条偏移的影响较小，但局部流速会发生改变，在任意两组防振条间流速和横流流体动能密度将平滑变化，且不会超过最近两跨的峰值.

［1］ Smith J C，Akeroyd J K. Applying experience in an advanced design(steam generators)[J]. Nuclear Engineering Internationa，1986，31(383)：83-86.

［2］ 叶 杰，蔡 伟，陈文虎. AP1000多根蒸汽发生器传热管破裂分析[J]. 原子能科学技术，2015，49(6)：1057-1061.

Ye Jie，Cai Wei，Chen Wenhu. Analysis of multiple steam generator tube rupture for AP1000[J]. Atomic Energy Science and Technology，2015，49(6)：1057-1061(in Chinese).

［3］ 杨 健，朱文韬. 蒸汽发生器传热管诱发破裂风险评估[J]. 核动力工程，2017，38(1)：51-55.

Yang Jian，Zhu Wentao. Risk evaluation for induced steam generator tube rupture[J]. Nuclear Power Engineering，2017，38(1)：51-55(in Chinese).

［4］ Qi J，Zhou K，Huang J，et al. Numerical simulation of the heat transfer of superheater tubes in power plants considering oxide scale[J]. International Journal of Heat and Mass Transfer，2018，122：929-938.

［5］ 刘春江，赵明恩，郭 凯，等. 基于流型结构构造的混合设备优化设计方法[J]. 天津大学学报：自然科学与工程技术版，2015，48(3)：255-261.

Liu Chunjiang，Zhao Ming’en，Guo Kai，et al. An approach to mixing equipment optimization based on flow pattern construction[J]. Journal of Tianjin University：Science and Technology，2015，48(3)：255-261(in Chinese).

［6］ Singhal A K，Srikantiah G. A review of thermal hydraulic analysis methodology for PWR steam generators and ATHOS3 code applications[J]. Progress in Nuclear Energy，1991，25(1)：7-70.

［7］ Patankar S V，Spalding D B. Computer analysis of the three-dimensional flow and heat transfer in a steam generator[J]. Forschung im Ingenieurwesen，1978，44(2)：47-52.

［8］ Patankar S V，Spalding D B. A calculation procedure for the transient and steady-state behavior of shell-and-tube heat exchangers[G]//Afgan N H，Schlunder E U. Heat Exchangers：Design and Theory Sourcebook. United States：Scripta Book Company，1974：156-176.

［9］ Lu Daogang，Wang Yu，Yuan Bo，et al. Development of three-dimensional thermal-hydraulic analysis code for steam generator with two-fluid model and porous media approach[J]. Applied Thermal Engineering，2017，116：663-676.

［10］ Hovi V，Pättikangas T，Riikonen V. Coupled one-dimensional and CFD models for the simulation of steam generators[J]. Nuclear Engineering and Design，2016，310：93-111.

［11］ Cong Tenglong，Zhang Rui，Tian Wenxi，et al. Effects of power level on thermal-hydraulic characteristics of steam generator[J]. Progress in Nuclear Energy，2015，81：245-253.

［12］ Cong Tenglong，Tian Wenxi，Qiu Suizheng，et al. Study on secondary side flow of steam generator with coupled heat transfer from primary to secondary side [J]. Applied Thermal Engineering，2013，61(2)：519-530.

［13］ 何 杰，高腾飞，罗文媛，等. 规整填料塔内气-液两相并流流动的CFD研究[J]. 化学工业与工程，2017，34(1)：76-83.

He Jie，Gao Tengfei，Luo Wenyuan，et al. Study on gas-liquid co-current flow in structured packing column by computational fluid dynamics[J]. Chemical Industry and Engineering，2017，34(1)：76-83(in Chinese).

［14］ Chull J J，Jun J J，Jo Y B，et al. Numerical prediction of a flashing flow of saturated water at high pressure[J]. Nuclear Engineering and Technology，2018，50(7)：1173-1183.

［15］ Schlichting H，Gersten K. Boundary-Layer Theory [M]. Berlin：Springer-Verlag，2017.

［16］ Launder B E，Spalding D B. Mathematical Models of Turbulence[M]. United States：Academic Press，1972.

［17］ Jiang F，Jiang T，Qi G P，et al. Effect of flow directions on multiphase flow boiling neat transfer enhanced by suspending particles in a circulating evaporation system[J]. Transactions of Tianjin Univeristy，2019，25(3)：201-213(in Chinese).

Simulation of Two-Phase Flow on the Secondary Side of PWR Steam Generator

Liu Liyan1，Su Tong1，Guo Kai1，Wang Yipeng1，Xiong Guangming1, 2，Zhu Yong2，Tan Wei1，Tang Guowu3

(1. School of Chemical Engineering and Technology，Tianjin University，Tianjin 300350，China； 2. China Nuclear Power Engineering Co.，Ltd.，Shenzhen 518124，China； 3. College of Chemistry，Chemical Engineering and Materials Science， Shandong Normal University，Jinan 250014，China)

In the steam generator of a pressurized water reactor nuclear power plant，secondary side fluid flowing through the heat transfer tube bundle causes the bundle to vibrate，which may damage the tube and cause an accident. Full-scale experiment and the numerical simulation method for studying the thermal-hydraulic characterization of the steam generator are difficult because of its large size and complex internal structure. Existing studies mainly focus on the thermo-hydraulic parameters under design conditions. Limited research is available regarding the distribution law of fluid force on the heat transfer tubes when the water supply ratio on the hot and cold side varies or when the anti-vibration bars produces displacement. Flow simulation software，FLUENT，is used to analyze flow field state and fluid force distribution law，and a porous model is established. Distributed resistance is used to characterize the influence of components such as tube bundle，support plate，and anti-vibration bar in the domain. The heat exchange energy between the primary and secondary sides is added to the model in the form of boundary conditions. Temperature distribution，vapour fraction，and velocity and transverse flow energies of the flow field is calculated based on the zero-equation turbulence model combined with the two-phase drift flow model. The influence of water supply ratio and anti-vibration bar offset on the fluid force distribution is also determined. Results show that under the design condition，the secondary side fluid rises to the boiling point and remains stable at the axial height of 3 m. The vapour fraction increases gradually during the heat exchange process，and the average value at the secondary side outlet is 90%. The fluid velocity is related to the vapour fraction，flow direction，and flow field structure. The average flow velocity on the hot side increases in the straight pipe section and decreases in the curved pipe section，reaching a maximum value of 5.36 m/s at the height of 8.8 m. The cold side has a slight decrease in the average flow velocity before the axial height of 2.2 m and the same trend as the hot side. The maximum value at the height of 8.8 m is 3.56 m/s. The fluid effect in the tube bundle is obvious in the inlet and bend regions，but not in the straight pipe bundle. The change in water supply ratio on the hot and cold sides only has a great influence on the distribution of fluid kinetic energy at the inlet. The anti-vibration bar offset will affect the local fluid force distribution，the flow velocity，and kinetic energy between two anti-vibration bars will change smoothly.

steam generator；thermo-hydraulic；numerical simulation；two-phase flow

TL333

A

0493-2137(2019)07-0745-09

10.11784/tdxbz201810034

2018-10-22；

2018-12-24.

刘丽艳（1977—  ），女，博士，副教授，Liuliyan@tju.edu.cn.

谭 蔚，wtan@tju.edu.cn.

(责任编辑：田 军)