一种基于RTK-GNSS技术的大跨径悬索桥动态特性分析方法

2019-04-26熊春宝张雪芳牛彦波朱劲松

天津大学学报(自然科学与工程技术版) 2019年7期

关键词：固有频率重构模态

熊春宝，张雪芳，牛彦波，朱劲松

熊春宝，张雪芳，牛彦波，朱劲松

(天津大学建筑工程学院，天津 300072)

大跨径桥梁；RTK-GNSS；集合经验模态分解；小波降噪；快速傅里叶变换；随机减量技术

随着科技的发展与进步，桥梁结构正朝着大跨、轻质、高强的方向发展．在服役过程中，这些轻质高强的大跨度桥梁极易受到风荷载、交通荷载以及地震荷载等因素的影响，所以为了保障桥梁的安全与稳定，防止灾难性的事故发生，亟需采用合理有效的技术监测手段对现役桥梁在动态荷载作用下的振动响应进行监测，这对于预防和避免桥梁事故具有重要的作用．采用理论分析方法识别桥梁的动态参数较为复杂，通常情况下通过建立桥梁的有限元模型，进行模态分析来获取桥梁结构的固有频率与振型，而结构的阻尼比往往凭经验取值．现如今，现场实测技术无疑是能够准确反映桥梁在复杂动态荷载作用下振动响应的最直接、最有效的手段．

传统的用于桥梁结构位移监测的方法有位移传感器法、全站仪法、应变片法、加速度计法等[1-4]．在大跨径桥梁结构健康监测领域，加速度计已经被证实是一种有效的监测手段，它通过二次积分可获取结构的坐标信息，并且具有频率高、响应快、性能稳定等特点[5]．但是，加速度计监测结果经过二次积分会快速发散，出现漂移现象，因此加速度计难以满足位移测量精度的要求[6]．相较于加速度计，全球卫星定位系统(GPS)能够很容易地得到结构的三维坐标信息，连续、实时、高效地反映结构的振动特性．RTK-GPS是一项基于载波相位双差模型的定位方法，也是GPS动态测量最精确的定位技术，在大型土木工程结构中得到了广泛的应用，如：李宏男等[7]利用RTK-GPS技术对大连某一超高层建筑进行了监测试验，并对监测结果进行巴特沃斯高通滤波处理，准确识别出了结构的一阶振动频率；Xiong等[8]利用RTK-GPS监测了天津117大厦，并利用切比雪夫高通滤波器对监测数据进行了处理，获得了较好的结果；许昌和岳东杰[9]利用RTK-GPS监测一斜拉桥高索塔，并通过频谱分析获取了该高索塔自立状态下的自振主频，与有限元分析的结果吻合；Yi等[10]利用RTK-GPS对一大跨径悬索桥在环境激励下的动态响应问题做了深入研究，结合有限元模型分析，准确获取了结构的固有频率．Elnabwy等[11]利用RTK-GPS对一铁路桥进行实时监测，基于移动平均滤波与神经网络自回归模型分析，准确获取了结构的三维动态位移．以上研究证实了RTK-GPS是一种强有力的获取结构动态变形的工具．目前，我国北斗卫星定位系统(BDS)正在逐步完善，多星系导航定位系统得到发展．与单星系GPS定位系统相比，多星系导航定位系统可见卫星数明显增多，位置精度因子(PDOP)明显减小，定位精度得到显著提升[12]．本文所采用的RTK-GNSS传感器能够同时接收GPS、GLONASS和BDS三星系卫星信号，能够更加准确地获取桥梁的振动响应信息，为结构的安全稳定提供更为可靠的依据．

影响结构振动监测精度的主要因素有两方面：一方面是传感器的选择，另一方面是信号处理方法．值得注意的是，RTK-GNSS传感器的定位精度是受限的，水平定位精度在±1cm左右，竖向定位精度在±2cm左右．而竖向振动为桥梁的主要形式，因此需要采用一种高效的数据处理方法来消除或削弱仪器误差给监测结果带来的影响．经验模态分解法(EMD)[13]是一种非线性、非稳态的信号处理方法．该方法将信号分解为一系列单成分的本征模态函数(IMF)，其实质是不同特征时间尺度的固有振动模式．然而，EMD法存在一些缺陷，如模态混叠现象．为了解决这个问题，Wu等[14]提出了一种新的方法，即集合经验模态分解(ensemble empirical mode decomposition，EEMD)法．该方法在待分解信号中加入了高斯白噪声，有效抑制了模态混叠现象．小波技术是一种高效的数据处理方法，在工程、金融、科学等领域得到了广泛的应用[15-18]．阈值降噪技术是小波降噪(WD)方法的一种，通过设定合理阈值处理小波分解系数，然后对信号进行重构，以达到降噪目的．为了保证结构的降噪精度，本文提出了一种联合降噪方法，即EEMDWD法，此方法充分结合了EEMD与WD技术的优势，有效抑制了待分析信号的低频噪声与高频噪声．

模态参数识别是桥梁结构健康监测的重要研究领域，已有许多比较成熟的参数识别方法，如对数衰减法、希尔伯特变换法、频域分解法等[19-21]．随机减量技术(RDT)是一种针对结构在未知激励作用下通过样本的分段平均获取结构自由振动响应的参数识别方法[22]，一经提出便得到了广泛的应用．

本文基于RTK-GNSS技术，对环境激励下天津富民桥的动态响应进行现场监测试验．首先，试验之前对RTK-GNSS传感器进行稳定性测试，以评估其测量精度．然后，利用EEMDWD联合降噪法对监测数据进行预处理，以提高RTK-GNSS定位精度．其次，建立结构的有限元模型，通过模态分析预测结构的振动频率与振型．同时，利用FFT法从RTK-GNSS降噪信号中提取结构的固有频率，并与加速计传感器识别结果进行对比，印证RTK-GNSS技术的可行性.最后，通过RDT分析，得到结构的阻尼比．

1 RTK-GNSS稳定性试验

本次试验所采用的仪器为Hi-Target公司出产的海星达H32接收机．为了确保桥梁监测试验的顺利进行，以及确定测试设备的可靠性和稳定性，研究仪器背景噪声对监测数据的影响.在试验开始之前，对仪器的稳定性进行了测试，如图1所示．选择一个开阔的地带，将5台仪器固定在地面上，其中1台作为参考站，另外4台作为流动站．在RTK工作状态下，参考站接收机将观测值及测点的三维坐标信息通过数据链传送给流动站，流动站实时采集观测数据，同时接收参考站传送的信息，并在系统内部进行实时差分处理，通过差分可有效消除卫星的轨道误差、卫星钟差、接收机钟差及电离层和对流层的折射误差．试验连续监测3h，采样频率设置为10Hz.

图1 稳定性试验示意

选择其中一个监测点进行分析，其余测点类似，此处不再赘述．理论上，监测点的位移应为零，但是由于系统误差的原因，实际监测的位移结果并不为零．图2(a)给出了测点竖向位移幅度．可以看出，仪器的竖向定位精度在2cm以内．均方根值(RMS)是评价仪器噪声水平的一个关键指标，通过计算可得RMS值为0.58cm．随后采用快速傅里叶变换法(FFT)，得到了位移的功率谱密度(PSD)函数，如图2(b)所示．可以看出，系统的低频噪声主要限制在0.06Hz以下，高频噪声为近似服从范围在10-12～ 10-7m2·s之间的高斯白噪声．本次试验所研究桥梁的固有频率大于0.06Hz，因此，系统的低频噪声可以通过一些常规的滤波方法消除，进而提高系统的定位精度，但是高频噪声却保留了下来．本文提出的联合降噪方法，不仅可以消除低频噪声，而且可以有效抑制高频噪声，进一步提高仪器的测量精度．

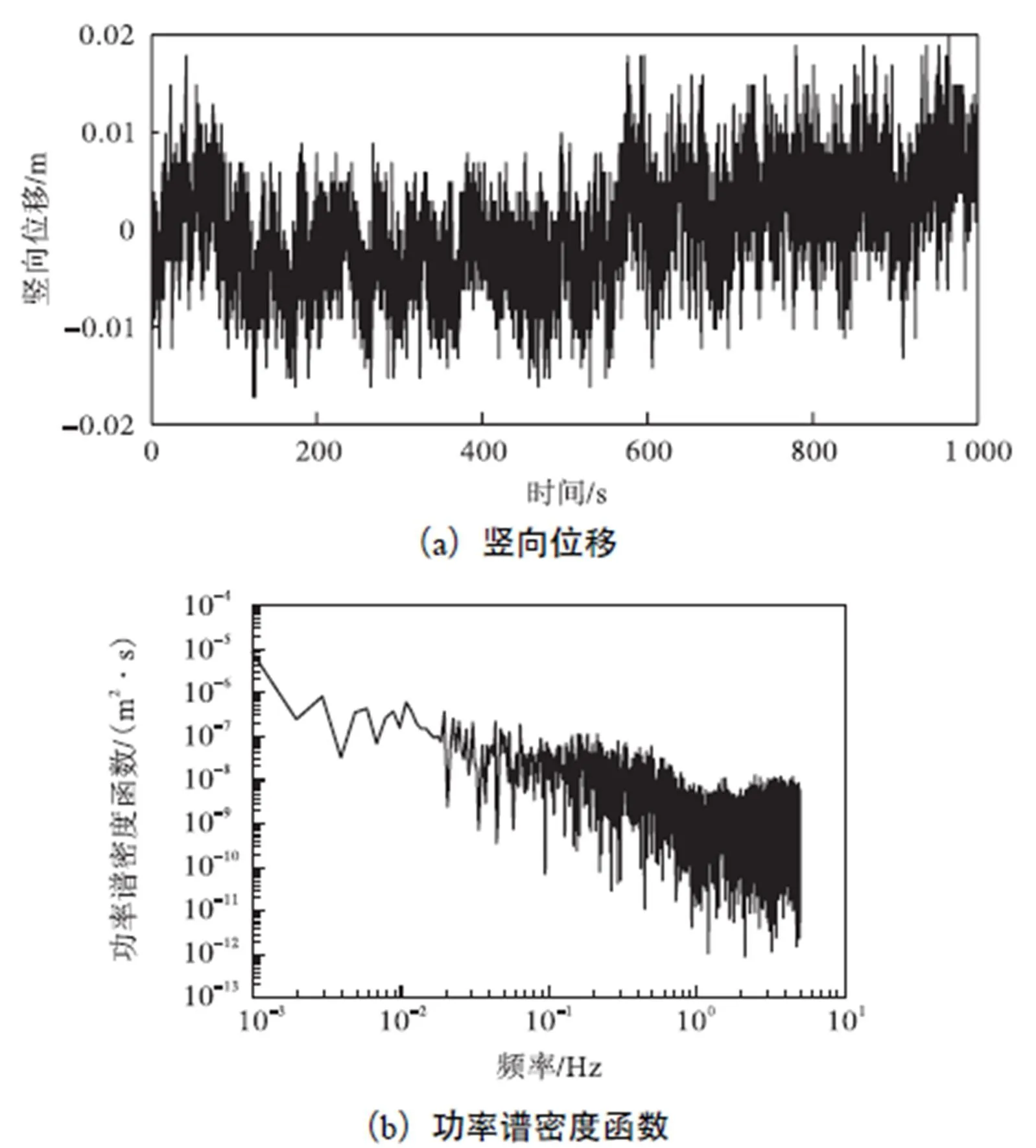
图2 稳定性试验的竖向位移及相应的功率谱密度函数

2 数据处理方法

2.1 EEMD算法

基于EMD算法，一个信号被分解为一系列本征模态函数，需要满足两个条件：①极值点和过零点的数目必须相等或者至多相差一个；②在任意时刻，上包络线与下包络线的均值为0．鉴于EMD算法是经验性的，缺乏严格的数学推导，因此，应用过程中带来了许多问题，如包络线拟合偏差、端点效应、模态混叠现象等．EEMD方法的提出很好地解决了模态混叠现象，具体算法如下．

(1) 在原始信号()中加入一组均值为0、方差相等的白噪声序列()，生成一个新的信号()，即

(1)

(2) 将信号()通过EMD算法分解为一系列本征模态函数IMF()和一个残余信号()，即

(2)

(3) 重复以上两步，得到组模态分量IMF()；

(4) 计算组模态分量的均值，作为最终的IMF.

(3)

2.2 小波降噪算法

小波阈值降噪可分为3步：首先，将原始信号进行小波变换，得到小波分解系数；然后，对系数进行阈值处理，过滤噪声信号；最后，信号重构输出结果．本文选择软阈值函数算法对系数进行处理．

软阈值法为

(4)

2.3 EEMDWD原理

本文提出的联合降噪方法充分结合了EEMD与小波的优势，具体分析步骤如下：

(1) 使用EEMD算法，获取一系列从高频至低频排列的本征模态函数IMF()；

(2) 去除不包含主频的部分低频信号与高频信号，这样相当于形成了一个带通滤波器，然后将剩余信号进行重构；

(3) 将重构信号进行小波3层分解；

(4) 对每一个小波分解系数，选择一个合适的阈值，对其进行阈值量化；

(5) 对信号进行二次重构，输出结果．

2.4 随机减量技术

RDT是一种时域信号处理方法，可以通过样本的分段平均来获取结构的特征信号，即随机减量信号．一个单自由度线性系统的动力方程可以表示为

(5)

系统的位移响应可以被表达为

(6)

(7)

(8)

(9)

(10)

(11)

式中代表随机减量信号一次循环的平均周期．

(12)

(13)

图3给出了本次数据处理的整个流程．

图3 数据处理流程

3 天津富民桥监测实例

3.1 工程概况及监测方案

天津富民桥(如图4所示)是一座单塔空间索面自锚式悬索桥，连接天津市河西、河东两区的重要跨河通道，车辆通过频繁，人在桥上振感明显，选择该桥梁作为研究对象，实时监测其振动响应，有利于保障结构的安全稳定与正常运行．主跨主缆锚固于主梁两侧，侧跨主缆锚固在重力锚碇上，形成了稳定的体系．全桥由3跨混凝土连续梁(19m＋20m＋79.6m)、单塔空间索面自锚式悬索桥(86.4m＋157.081m)和单悬臂混凝土框架结构(38.219m)组成．桥梁全宽38.6m，横向排列依次为0.8m(吊索锚固区)＋0.5m(碰撞保护)＋14.5m(3.75m的非机动车道＋(3.75m＋2×3.5m)机动车道)＋0.5m(路带)＋0.5m(碰撞障碍)＋5m(主塔区)＋0.5m(防撞护栏)＋0.5m(路带)＋14.5m(3.75m的非机动车道＋(3.75m＋2×3.5m)机动车道)＋0.5m(碰撞保护)＋0.8m(吊索锚固区)．

图4 天津富民桥示意

RTK-GNSS传感器是监测大跨径桥梁的有效工具，本次试验总共采用7台RTK-GNSS传感器对整个桥梁进行实时监测，采集频率设置为10Hz，其中1台作为参考站接收机，其余6台作为流动站接收机．在距离桥梁约120m的空阔且视线无遮挡地方布置参考站接收机，如图5(a)所示．在桥梁主跨的两侧对称布置流动站接收机，另外，为了与RTK-GNSS监测结果进行对比，在主跨跨中2点处，布置一台加速度计传感器，如图5(b)和5(c)所示，即测点1～6．

3.2 桥梁的有限元模型

为了与实测结果进行对比，在此采用有限元软件ANSYS建立了桥梁的有限元模型，如图6(a)所示．在模型中，主塔、横梁、纵梁、墩柱采用BEAM44单元进行模拟，主缆和吊杆采用LINK10单元进行模拟．模型的每个节点均有6个自由度：沿、、方向的平移自由度与绕、、轴的转动自由度．经过数值分析，很容易得到结构的前5阶固有频率，分别为0.5705Hz、0.9707Hz、1.1290Hz、1.4009Hz和1.7880Hz，见图6(b)～(f)．可以看出，结构的振动模态较为密集，在一个很窄的频带上，许多振动模态都可能被激发．因此，对结构进行实时监测很有必要.

图5 天津富民桥监测实验照片及示意

3.3 振动信号分析

根据Nyquist采样定理，当采样频率大于信号的最高频率的２倍时，可完整地保留原始信号中的信息.根据有限元分析结果，结构的1阶固有频率为0.5705Hz，本次试验RTK-GNSS采集频率设置为10Hz，加速度计采集频率设置为50Hz，完全满足要求.

试验连续监测10h，根据有限元模型分析结果可知，测点2与5为桥梁的最不利截面，由于对称性，以测点2为例作进一步分析．图7给出了原始信号的位移幅度及其功率谱密度函数，可以看出，结构的位移在-0.0537～0.0541m之间变化，相应的功率谱密度函数在0.5873Hz处存在峰值，对应于结构的最低阶固有频率．图8给出了加速度信号及其功率谱密度函数，可以看出，固有频率识别结果与RTK-GNSS相一致，印证了RTK-GNSS应用于桥梁动态特性监测的可行性．然而，基于稳定性试验可知，RTK-GNSS信号中包含大量的低频与高频噪声．因此，下一步将采用EEMDWD联合降噪方法对RTK-GNSS信号进行处理．首先，利用EEMD算法对原始信号进行分解，得到14个IMF分量，分别对每个分量利用FFT法得到信号的功率谱密度函数，如图9和图10所示．可以看出，信号的主频主要分布在2～6阶IMF分量上，为了降低噪声的影响，将第1阶分量与第8～14阶分量移除，相当于形成一个带通滤波器，然后将其余分量进行重构．

图6 桥梁有限元模型及其各阶模态

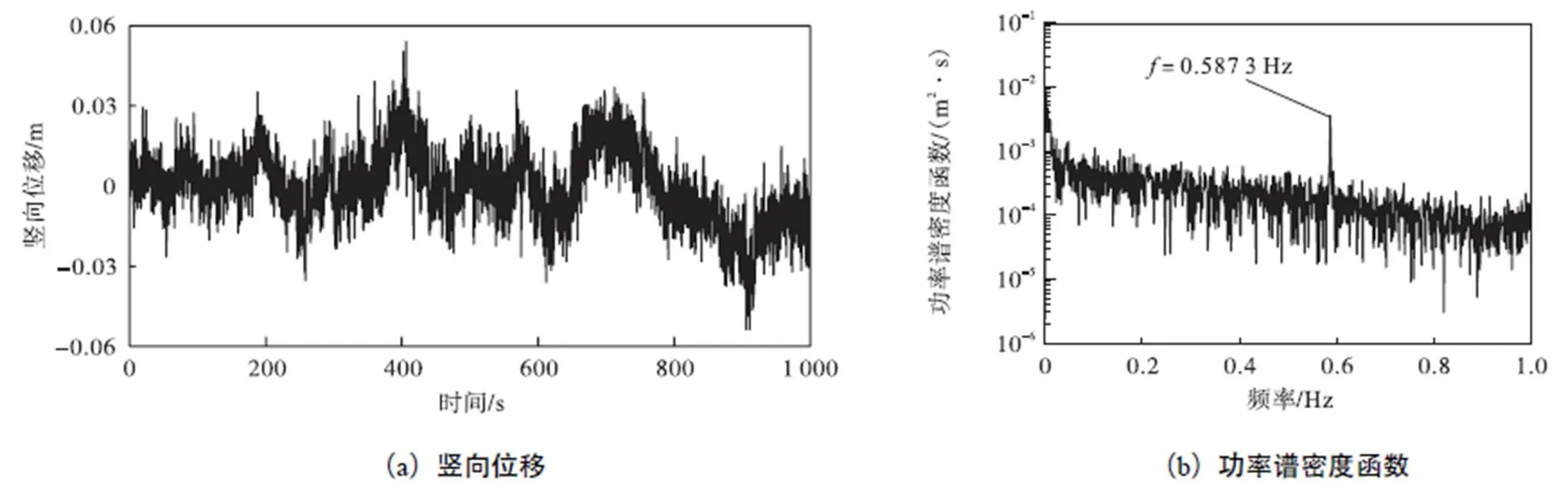
图7 测点C2处位移及其功率谱密度函数

图8 测点C2处加速度及其功率谱密度函数

图9 原始位移信号的IMF分量及其功率谱密度函数(IMF1～IMF7)

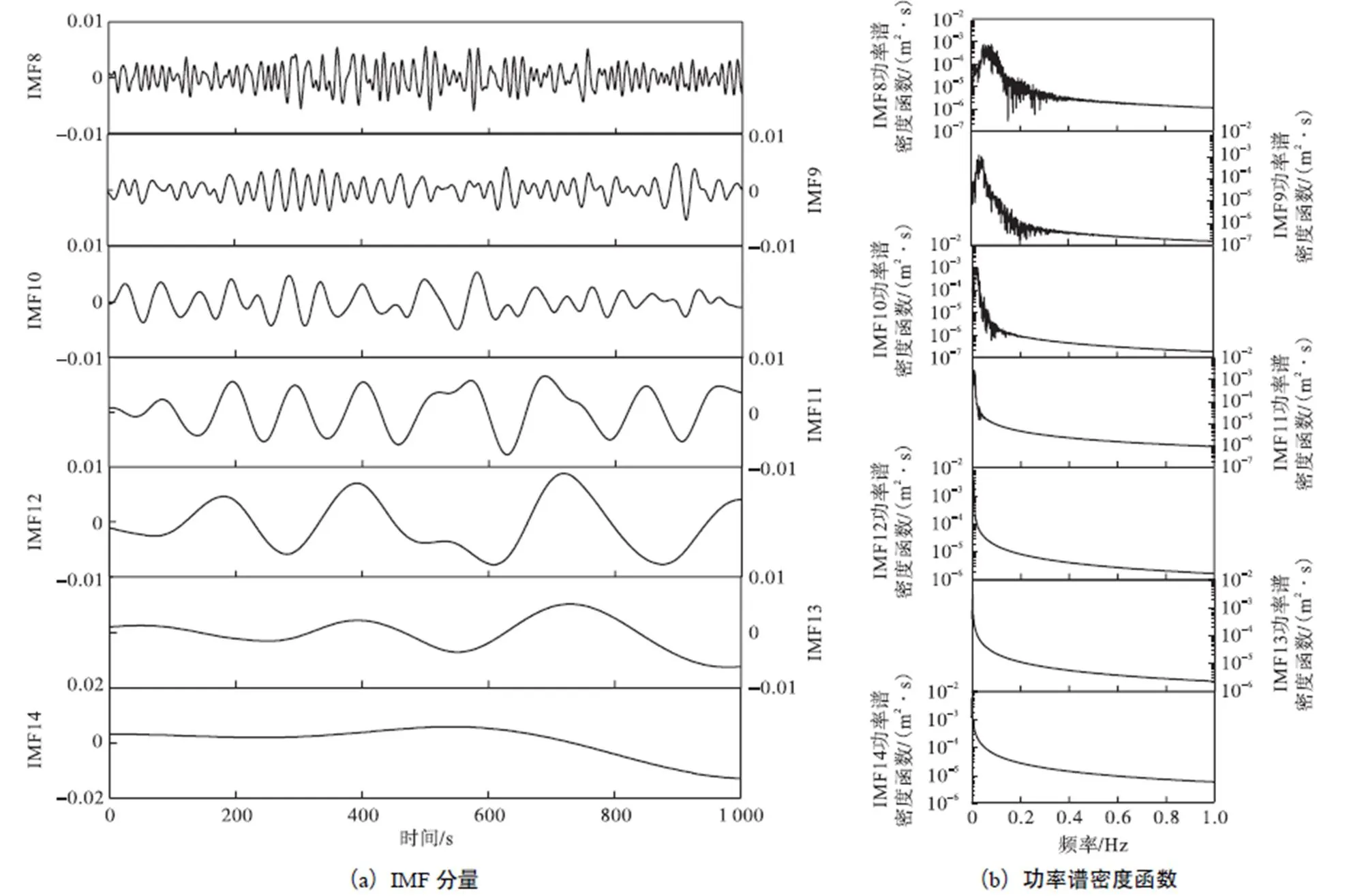
图10 原始位移信号的IMF分量及其功率谱密度函数(IMF8～IMF14)

图11给出了重构后信号R1(位移幅度：-0.0248～0.0262m)及其功率谱密度函数．相比于原始信号，重构后的信号位移幅度明显减小，低频噪声得到了有效的抑制．对于重构后的信号进行3层小波降噪，图12给出了二次重构信号R2(位移幅度：-0.0239～0.0254m)及其功率谱密度函数．为了对比EEMD、WD、EEMDWD三者降噪效果，图13给出了原始信号采用单独小波降噪技术得到的结果，即信号R3(位移幅度：-0.0471～0.0467m)．随后，基于Hilbert变换，分别对原始信号、WD降噪信号、EEMD降噪信号及EEMDWD降噪信号进行时频分析，结果如图14所示．对比图14(a)与14(b)，可以看出原始信号经过小波降噪，高频噪声得到了有效的抑制，然而低频噪声降噪效果并不明显．对比图14(a)与14(c)，可以看出信号经过EEMD降噪，低频噪声与部分高频噪声得到了有效的抑制．对比图14(b)、14(c)与14(d)，可以看出与单独采用EEMD或者WD方法相比较，EEMDWD降噪效果更为明显．分别计算原始信号、信号R3、信号R1和信号R2的均方根值，可得结果为0.0224m、0.0217m、0.0095m和0.0074m.基于以上讨论，可知联合降噪法优于单独采用EEMD与WD法．

阻尼比是结构动态特性的一个重要参数，通常在设计模型中根据经验取值，本文根据实测数据采用RDT法来估计结构的阻尼比具有重要的意义．根据前人宝贵的研究，子样本数的取值在400～2000之间，本次试验取为1500，时间间隔取为100s，经过计算可得测点的随机减量信号如图15所示，进一步可估计结构的阻尼比为＝2.12%．至此，已成功拾取到了结构的动态参数．

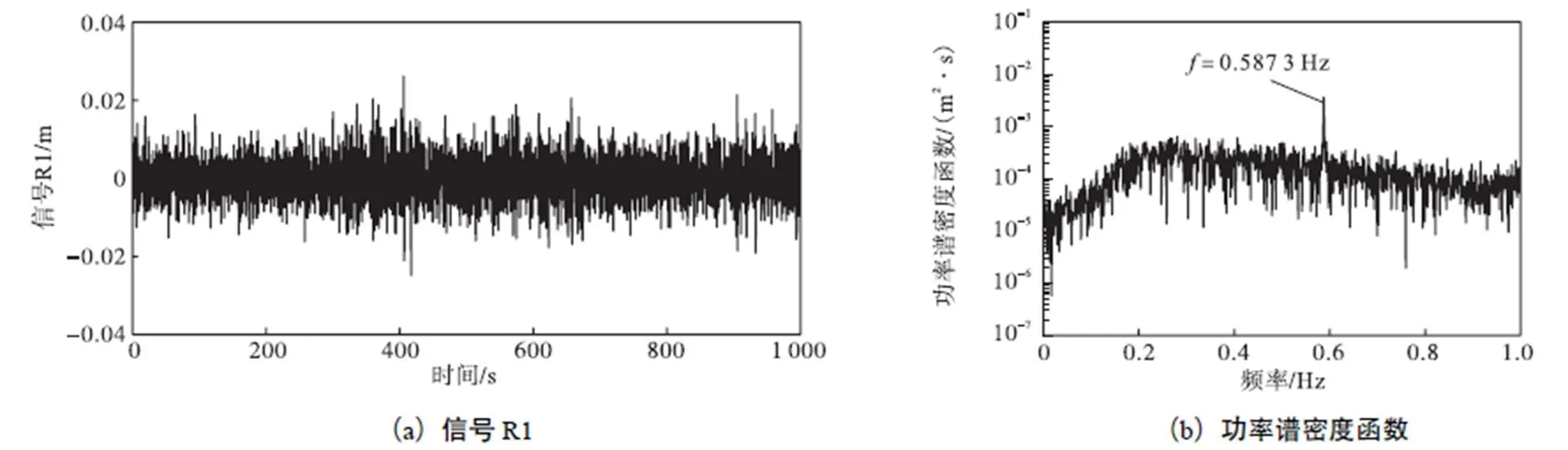
图11 一次重构信号R1与其功率谱密度函数

图12 二次重构信号R2及其功率谱密度函数

图13 小波降噪信号R3及其功率谱密度函数

图14 Hilbert能量谱

图15 信号R2的随机减量信号

4 结论

(1) 通过RTK-GNSS稳定性试验分析，可以得到，传感器误差主要来源于两部分：高能量的低频背景噪声以及低能量的高频白噪声．经过Hilbert谱分析可以看出，文中提出的联合降噪方法(EEMDWD)明显优于单独的EEMD与WD法，该方法不仅可以有效抑制低频噪声，而且可以消除高频噪声的影响，使得RTK-GNSS定位精度有了大幅提升．

(2) 通过FFT分析，分别从RTK-GNSS信号与加速度信号中提取结构的固有频率，所得结果比较一致．这说明RTK-GNSS应用于监测环境激励下大跨径桥梁结构的动态响应是可行的，且可以克服由加速度计二次积分得到位移所产生的趋势项无法消除的缺陷，有着广泛的应用前景．

(3) 通过建立结构的有限元模型，得到了结构前5阶固有频率及相应的振型．对比一阶固有频率拾取结果，可以发现，实测值与数值模拟结果基本吻合，两者相差2.86%．这也进一步表明，对于实时监测大跨径桥梁的动态响应信息，RTK-GNSS技术是一种强有力的工具．

(4) 通过RDT分析，从RTK-GNSS信号中提取结构的随机减量信号，再利用对数衰减法得到结构的阻尼比．至此，笔者已经成功得到了结构的一阶固有频率及相应的阻尼比，即＝0.5873Hz、＝2.12%．

［1］ Rodrigues C，Félix C，Figueiras J. Fiber-optic-based displacement transducer to measure bridge deflections [J]. Structural Health Monitoriing，2010，10(2)：147-156.

［2］ Yu J Y，Zhu P，Xu B，et al. Experimental assessment of high sampling-rate robotic total station for monitoring bridge dynamic responses[J]. Measurement，2017，104：60-69.

［3］ Wang T，Tang Y S. Dynamic displacement monitoring of flexural structures with distributed long-gage macro-strain sensors[J]. Advances in Mechanical Engineering，2017，9(4)：1-12.

［4］ Sekiya H，Kimura H，Miki C. Technique for determining bridge displacement response using MEMS accelerometers[J]. Sensors，2016，16(2)：257-266.

［5］ Fenerci A，Øiseth O，Rønnquist A. Long-term monitoring of wind field characteristics and dynamic response of a long-span suspension bridge in complex terrain[J]. Engineering Structures，2017，147：269-284.

［6］ Masri S F，Sheng L H，Caffrey J P，et al. Application of a web-enabled real-time structural health monitoring system for civil infrastructure systems[J]. Smart Materials and Structures，2004，13(6)：1269-1283.

［7］李宏男，伊廷华，伊晓东，等. 基于RTK GPS技术的超高层结构风振观测[J]. 工程力学，2007，24(8)：121-126.

Li Hongnan，Yi Tinghua，Yi Xiaodong，et al. Measurement of wind induced response of tall building based on RTK GPS technology[J]. Engineering Mechanics，2007，24(8)：121-126(in Chinese).

［8］ Xiong C B，Niu Y B. An investigation of the dynamic characteristics of super high-rise buildings using real-time kinematic-global navigation satellite system technology[J]. Advances in Structural Engineering，2018，21(5)：783-792.

［9］许昌，岳东杰. 基于RTK-GPS技术的高索塔振动试验与分析[J]. 振动与冲击，2010，29(3)：134-136.

Xu Chang，Yue Dongjie. Ambient vibration test of high pylon based on RTK-GPS technology[J]. Journal of Vibration and Shock，2010，29(3)：134-136(in Chinese).

［10］ Yi T H，Li H N，Gu M. Full-scale measurements of dynamic response of suspension bridge subjected to environmental loads using GPS technology[J]. Science China Technological Sciences，2010，53(2)：469-479.

［11］ Elnabwy M T，Kaloop M R，Elbeltagi E. Talkha steel highway bridge monitoring and movement identification using RTK-GPS technique[J]. Measurement，2013，46(10)：4282-4292.

［12］ Li X，Zhang X，Ren X，et al. Precise positioning with current multi-constellation global navigation satellite systems：GPS，GLONASS，Galileo and BeiDou[J]. Scientific Reports，2015，5：8328-8341.

［13］ Huang N E，Shen Z，Long S R，et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Roval Society A：Mathematical Physical and Engineering Sciences，1998，454：903-995.

［14］ Wu Zhaohua，Huang N E. Ensemble empirical mode decomposition：A noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis，2009，1：1-41.

［15］张淑芳，黄小琴. 基于背景消除的小波域视频质量评价模型[J］. 天津大学学报：自然科学与工程技术版，2017，50(12)：1255-1261.

Zhang Shufang，Huang Xiaoqin. Video quality assessment model in wavelet domain based on background subtraction[J]. Journal of Tianjin University：Science and Technology，2017，50(12)：1255-1261(in Chinese).

［16］焦敬品，于兆卿，刘文华，等. 基于小波变换的薄层厚度电磁超声测量方法[J]. 仪器仪表学报，2013，34(3)：588-595.

Jiao Jingpin，Yu Zhaoqing，Liu Wenhua，et al. Electromagnetic acoustic thickness measurement method of thin liquid layer based on wavelet transform[J]. Chinese Journal of Scientific Instrument，2013，34(3)：588-595(in Chinese).

［17］ Huang S C，Wu T K. Integrating recurrent SOM with wavelet-based kernel partial least square regressions for financial forecasting[J]. Expert Systems with Applications，2010，37(8)：5698-5705.

［18］吴一全，王志来. 基于小波域改进SURF的遥感图像配准算法[J]. 天津大学学报：自然科学与工程技术版，2017，50(10)：1084-1092.

Wu Yiquan，Wang Zhilai. Remote sensing image registration algorithm based on improved SURF in wavelet domain[J]. Journal of Tianjin University：Science and Technology，2017，50(10)：1084-1092 (in Chinese).

［19］ Nakutis Ž，Kaškonas P. Bridge vibration logarithmic decrement estimation at the presence of amplitude beat[J]. Measurement，2011，44(2)：487-492.

［20］ Huang N E，Wu Z H. A review on Hilbert-Huang transform：Method and its applications to geophysical studies[J]. Reviews of Geophysics，2008，46(2)：1-23.

［21］ Brincker R，Zhang L，Andersen P. Modalidentification from ambient responses using frequencydomain decomposition[C]//Proceeding of 18th International Modal Analysis Conference. San Antonio，Texas，USA，2000：625-630.

［22］ Cole H A. Method and Apparatus for Measuring the Damping Characteristic of AStructure：USA，3620069[P]. 1971-11-16.

A Method for Analysing the Dynamic Characteristics of a Long-Span Suspension Bridge Based on RTK-GNSS Technique

Xiong Chunbao，Zhang Xuefang，Niu Yanbo，Zhu Jinsong

(School of Civil Engineering，Tianjin University，Tianjin 300072，China)

long-span bridge；RTK-GNSS；ensemble empirical mode decomposition(EEMD)；wavelet decomposition；fast Fourier transform；random decrement technique

10.11784/tdxbz201807018

TU317

0493-2137(2019)07-0699-10

2018-07-11；

2018-09-20.

熊春宝（1964— ），男，博士，教授.

熊春宝，luhai_tj@126.com.