高考动量命题的切入点

湖北 许 文

解读动量考点 探索命题规律

用动量定理、动量守恒定律不仅可以分析物体在恒力作用下的运动问题，也可以分析在变力作用下的运动问题。动量考点知识可以与持续作用问题、能量问题、电磁感应问题、原子物理问题等知识内容相结合，有时也会伴随着极值问题与临界问题。高考中与动量知识考点相关的题型一般以选择题和计算题为主，也有实验题。因此动量相关知识可以全面考查考生运用物理学的研究方法，建构物理模型的能力，考查考生的空间想象能力与应用数学知识分析处理物理问题的能力，考查定性分析与定量研究相结合的分析能力。从2017年起，全国高考物理大纲将以往选修动量内容调整为必修内容，这一调整在2017年与2018年两年高考全国三套卷中都有所体现。高考考纲对动量、动量定理、动量守恒定律及应用的要求等级为Ⅱ(即能对动量、动量定理、动量守恒定律理解其确切含义及与其他知识间的联系，能够进行叙述和解释，并能在实际问题的分析、综合、推理和判断等过程中运用)，知道弹性碰撞与非弹性碰撞。本文解读高考动量考点，探索高考命题规律。

一、两年动量考点概述

卷名2017年2018年题号考点题号考点全国卷Ⅰ14动量守恒定律24动量与能量守恒全国卷Ⅱ15动量概念15动量定理24动量守恒定律全国卷Ⅲ20动量与冲量25(2)动量概念北京卷23动量守恒定律与原子核反应22冲量与动量定理天津卷10动量定理与能量守恒定律12动量定理与电磁感应12动量定理与电磁感应江苏卷12C(2)动量概念12C(3)动量守恒定律12C(3)动量定理海南卷1动量守恒定律14动量与能量守恒

二、动量考点解读与预测

1.动量与冲量

【例1】(2017年全国卷ⅢT20)一质量为2 kg的物块在合外力F的作用下从静止开始沿直线运动。F随时间t变化的图线如图1所示，则

( )

A.t=1 s时物块的速率为1 m/s

B.t=2 s时物块的动量大小为4 kg· m/s

C.t=3 s时物块的动量大小为5 kg· m/s

D.t=4 s时物块的速度为零

图1

【答案】AB

【点睛】F-t图象中图线与坐标轴围成的“面积”表示力的冲量大小。

【小结】物体的动量p=mv是状态量，v指物体的瞬时速度，具有相对性，一般选取相对地面静止的物体为参考系；同一物体的动量大小p与动能Ek的关系p2=2mEk；力的冲量I=Ft是过程量，其中力F为恒力。动量与冲量均为矢量，物体所受合力的冲量等于各力冲量的矢量和。

【预测】理解动量与冲量的区别，计算物体在某一状态时的动量与力在某一过程中的冲量。动量、冲量常与动能、功等问题相结合进行考查。

2.动量定理

【例2】(原创)如图2所示，一架质量为M的救援武装直升机的旋翼桨旋转向下推空气获得反冲力使直升机悬停在空中。已知直升机发动机的功率为P，则单位时间内向下推出空气的质量为

( )

图2

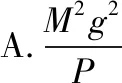
【解析】设发动机带动旋翼桨旋转在一段很短的时间Δt内使质量为Δm的一团空气体获得向下的速度v，发动机对这团气体的作用力为F(F≫Δmg)，直升机获得反冲力F′而停在空中不动。

对直升机有F′=Mg；由牛顿第三定律得F=F′=Mg

对这团气体由动量定理有FΔt=Δmv

【答案】C

【点睛】持续作用问题又称流体问题。对于流体的持续作用问题，关键的是正确建立物理模型，选取合适的研究对象，应用动量定理求解。

【小结】建立“柱状模型”，解决持续作用问题。

问题特点通常液体流、气体流等被广义地视为“流体”,质量具有连续性,通常已知密度ρ分析步骤1建立“柱状”模型,沿流速v的方向选取一段柱形流体,其横截面积为S2微元研究,作用时间Δt内的一段柱形流体的长度为Δl,对应的质量为Δm=ρSvΔt3建立方程,应用动量定理研究这段柱状流体

【例3】(2018年天津卷T12)真空管道超高速列车的动力系统是一种将电能直接转换成平动动能的装置。图3是某种动力系统的简化模型，图中粗实线表示固定在水平面上间距为l的两条平行光滑金属导轨，电阻忽略不计，ab和cd是两根与导轨垂直，长度均为l，电阻均为R的金属棒，通过绝缘材料固定在列车底部，并与导轨良好接触，其间距也为l，列车的总质量为m。列车启动前，ab、cd处于磁感应强度为B的匀强磁场中，磁场方向垂直于导轨平面向下，如图3所示，为使列车启动，需在M、N间连接电动势为E的直流电源，电源内阻及导线电阻忽略不计，列车启动后电源自动关闭。

图3

(1)要使列车向右运行，启动时图3中M、N哪个接电源正极，并简要说明理由；

(2)求刚接通电源时列车加速度a的大小；

(3)列车减速时，需在前方设置如图4所示的一系列磁感应强度为B的匀强磁场区域，磁场宽度和相邻磁场间距均大于l。若某时刻列车的速度为v0，此时ab、cd均在无磁场区域，试讨论：要使列车停下来，前方至少需要多少块这样的有界磁场？

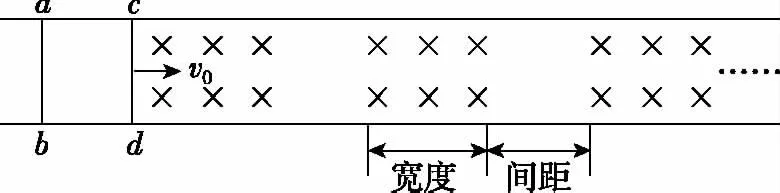
图4

【解析】(1)M接电源正极。列车要向右运动，安培力方向应向右，根据左手定则，接通电源后，金属棒中电流方向由a到b，由c到d，故M接电源正极。

两根金属棒所受安培力之和为F=BI0l

根据牛顿第二定律有F=ma

(3)设列车减速时，cd进入磁场后经Δt时间ab恰好进入磁场，此过程中穿过两金属棒与导轨所围回路的磁通量的变化为ΔΦ，平均感应电动势为E1。

cd受到的平均安培力为F1=BI1l

以向右为正方向，在Δt时间内cd受安培力的平均冲量为IA=-F1Δt

同理可知，回路出磁场时ab受安培力冲量与cd进入磁场过程中受到安培力的平均冲量相同。

设经过n块有界磁场区域后列车停下来，全过程中由动量定理有2nIA=0-mv0

【小结】动量定理表明冲量既是物体动量发生变化的原因，又是物体动量变化的量度。在动量定理中，合外力的冲量可以是恒力的冲量，也可以是变力的冲量。当合外力为变力时，其冲量应指在作用时间内的平均值。动量定理研究的是一个过程，解题时必须明确物体在过程初末状态的动量；动量定理的表达式是矢量式，在一维情况下，各个矢量必须选一个统一的正方向。

【预测】由动量的变化通过动量定理计算变力的冲量或变力的平均值。动量定理常与持续作用问题、电磁感应等问题相结合进行考查。

3.动量守恒定律

【例4】如图5所示，一块足够长的木板放在光滑水平面上。在木板上自左向右依次放有序号为1、2、3…n号的木块，它们的质量均为m，与木板间的动摩擦因数相同。开始时木板静止不动，第1、2、3…n号木块分别以初速度v0、2v0、3v0…nv0同时运动，v0方向水平向右，已知木板的质量与所有木块的总质量相等。最终所有木块与木板以共同的速度匀速运动。设木块之间均无碰撞，求：

(1)所有木块与木板一起匀速运动的速度vn；

(2)第k(k

图5

(2)由于所有木块与木板间的动摩擦因数相同，由牛顿运动定律知，在与木板相对静止前所有木块均先以相同的加速度做匀减速运动，在与木板相对静止后再随木板一起做加速运动。故当木块与木板相对静止时的速度即为此木块在整个运动过程中的最小速度。

设第k(k

木板的动量变化为Δp2=nmvk；

第k个木块以后的(n-k)个木块还在相对木板运动，此过程中它们受到的动摩擦力的冲量相同，其动量的变化量相同，故后(n-k)个木块的总动量变化量是第k个木块动量变化的(n-k)倍，即为Δp3=(n-k)(mvk-kmv0)；

由于系统的总动量守恒，有Δp1+Δp2+Δp3=0；

【点评】本题第(2)问是个难点，由于参与作用的物体较多，且每个物体的运动情况又不完全相同，作用的情况比较复杂，让人觉得眼花缭乱，无从下手。以上求解中从巧选研究对象和过程上找到了解题的突破口，灵活的运用动量守恒定律的表达式进行求解，有效地化解了难点。

【点睛】本题中当第k(k

【小结】动量守恒定律的两种数学表示形式及物理意义如下：

形式表达式物理意义总量式p=p′系统在某两个状态时的总动量相等增量式Δp1=-Δp2系统内两物体动量的增量大小相等、方向相反Δp=0系统内各物体动量增量的矢量和为零

对多体系统，若能合理地选取小系统或作用阶段，灵活的运用动量守恒定律的表达式，问题的求解就会变得简洁。要注意的是对研究对象及过程的选取既要符合动量守恒定律的条件，又要方便解题。

(1)第一次碰撞后瞬间A和B速度的大小；

(2)A、B均停止运动后，二者之间的距离。

图6

【解析】(1)设小物块A从高h处由静止开始沿轨道下滑到水平轨道时的速度为v0

(2)假设A、B第一次碰后A停止位置在O点右侧距O点距离xA，B停止位置距O点距离xB。

由于xA>xB，这是不可能的。A应在B第一次碰后停止的位置与B发生第二次碰撞。

设第二次碰撞前A的速度为vA1。

设A与B第二次碰后的速度分别为vA2、vB2，由动量守恒定律与机械能守恒有

【点睛】弹性碰撞遵循动量守恒与能量守恒。由于碰撞时间极短，物体在碰撞相互作用过程中发生的位移很小，一般可忽略不计，可以认为物体碰撞后仍然从碰撞前的位置以新的动量开始运动。

【小结】动量守恒定律与能量守恒定律(或机械能守恒定律)、动能定理都只考查一个物理过程的始末两个状态有关物理量间的关系，对相互作用过程的细节不予细究，但对多体多过程问题要注意物体运动过程的分析。

【例6】用电子碰撞静止的原子，使原子从基态跃迁到激发态。设电子质量为m，原子质量为M，原子基态与激发态的能量差为ΔE，求入射电子初动能的最小值。

【点睛】电子与原子的“碰撞”过程遵循能量守恒定律与动量守恒定律。此“碰撞”过程中损失的机械能被原子吸收，等于基态的原子跃迁到激发态而增加的原子能量。

【小结】动量守恒定律是自然界中最普遍的规律，它们不仅适用于宏观低速运动的物体，也适用于微观高速运动的粒子。

【预测】在碰撞、爆炸、打击、反冲等物理现象中，一般会隐含有系统机械能与其他形式能量之间的转化，但这类问题因作用时间极短，且内力一般远大于外力，系统的动量或某方向上的动量守恒。动量守恒定律常与能量守恒定律、牛顿运动定律、多体多过程问题、电磁感应中的双滑杆问题、原子核反应问题等相结合进行考查。