动量定理在电学题型中的应用分析

浙江 章慧雄 陆 晖

“动”“电”结合题不易，冲量公式来解决。

随着新课改的推进，教育部正式公布2017年普通高考考试大纲中涉及了动量知识，浙江省在2014年已将动量作为加试部分的重点考查对象，近几次选考真题中都考查动量知识，分值大，区分度明显，因此，研究该类问题有较大的教学价值。笔者通过分析浙江近几次选考真题，归纳为以下两种考查类型。

一、微观粒子在磁场中与宏观对象相作用，主要研究作用力的冲量

图1

(1)求离子束从小孔O射入磁场后打到x轴的区间；

(2)调整磁感应强度的大小，可使速度最大的离子恰好打在探测板右端，求此时的磁感应强度大小B1；

(3)保持磁感应强度B1不变，求每秒打在探测板上的离子数N；若打在板上的离子80%被吸收，20%被反向弹回，弹回速度大小为打板前速度大小的0.6，求探测板受到的作用力大小。

根据动量定理，吸收的离子受到板的作用力大小

反弹的离子受到板的作用力大小

根据牛顿第三定律，探测板受到的作用力大小

【评析】粒子在磁场中运动时，当涉及的受力以洛伦兹力为主，运动为圆周运动或部分圆周运动时，可以利用洛伦兹力的冲量求解偏转量，具体表达式可表示为qBx=mvy2-mvy1，qBy=mvx2-mvx1。当涉及粒子与粒子或与接触物碰撞、吸收、反弹时，学生的易错点及难点主要集中在分析粒子作用问题时，会遗漏粒子个数或求解粒子总数，导致解题出错。若选择恰当的研究对象，则作用力的大小可以利用动量定理分析。

【教学策略一】收集整理同类题型，彼此融通，知识内化

题型一以光压问题为例

科学家们设想在太空中利用太阳帆船进行星际旅行——利用太空中阻力很小的特点，制作一个面积足够大的帆接收太阳光，利用光压推动太阳帆船前进，进行星际旅行。假设在太空中某位置，太阳光在单位时间内、垂直通过单位面积的能量为E0，太阳光波长的均值为λ，光速为c，太空帆的面积为A，太空船的总质量为M，光子照射到太阳帆上的反射率为百分之百，求太阳光的光压作用在太空船上产生的最大加速度是多少？

【点评】收集类似光压、离子推进器(粒子的反冲)、火箭等问题，将该类问题总结归纳，解题的关键是选择好研究对象，把所有微观粒子处理成整体对象与宏观对象实施作用，产生作用力，再运用动量定理FΔt=mv2-mv1求解，帮助学生融会贯通，用好动量定理解决不同情境的微观粒子与磁场相互作用问题。

【教学策略二】收集整理相异题型，对比辨析，方法强化

题型二以扭摆器问题为例

【2011年山东卷，改篇】简化模型如图2中Ⅰ、Ⅱ两处的条形匀强磁场区边界竖直，相距为L，磁场方向相反且垂直纸面。一质量为m、电荷量为-q、重力不计的粒子，从靠近平行板电容器MN板处由静止释放，极板间电压为U，粒子经电场加速后平行于纸面射入Ⅰ区，射入时速度与水平方向夹角θ=30°。若B1≠B2、L1≠L2，且已保证了粒子能从Ⅱ区右边界射出。为使粒子从Ⅱ区右边界射出的方向与从Ⅰ区左边界射入的方向总相同，求B1、B2、L1、L2之间应满足的关系式。

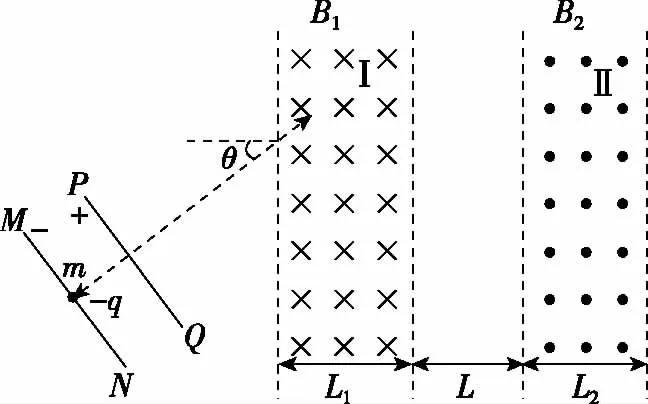
图2

【点评】该类问题与题型一不同，从方法分析，突出微观粒子整体观解题的特殊性。粒子从Ⅰ、Ⅱ区穿出，在y方向由动量定理，分析洛伦兹力的冲量，qBx=mvy2-mvy1，得qB1L1-qB2L2=mΔvy=0，比常规解法有明显优势。本题可以作为洛伦兹力的动量定理典型应用题，教学时，借助对比分析，帮助学生在解题方法上强化动量定理的使用技巧，在面对新问题时，能够根据其某方面的特征线索，进行类推，与以往解决问题的经验相联系，形成解决问题的思路。

根据上述策略，围绕动量、冲量主题组织教学，帮助学生形成与该主题相关的、可解决问题的全面表征。比如在专题复习时开设“宇宙航行中的粒子的动量问题”专题课，综合介绍火箭推进器、光帆推进器、粒子推进器以及弹弓效应(动量守恒)等宇宙飞行器的动力方式；同时运用动量定理、动量守恒定律、机械能守恒定律、光子动量、喷射粒子束与电流及电荷量关系等知识解决相应问题。讲清“变质量气体问题”“带电粒子在复合场中的运动问题”，形成围绕该主题的整体表征，树立物理观念。

二、导体棒在电磁感应中与电路结合，主要研究安培力的冲量

【2018年11月浙江选考真题】如图3所示，在间距L=0.2 m的两光滑平行水平金属导轨间存在方向垂直于纸面(向内为正)的磁场，磁感应强度的分布沿y方向不变，沿x方向如下：

图3

导轨间通过单刀双掷开关S连接恒流源和电容C=1 F的未充电的电容器，恒流源可为电路提供恒定电流I=2 A，电流方向如图3所示。有一质量m=0.1 kg的金属棒ab垂直导轨静止放置于x0=0.7 m处。开关S掷向1，棒ab从静止开始运动，到达x3=-0.2 m处时，开关S掷向2。已知棒ab在运动过程中始终与导轨垂直。求：(3)电容器最终所带的电荷量Q。[(1)(2)略]

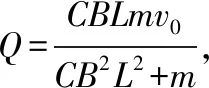
【评析】电流通过直导线时，在磁场中要受到安培力的作用。当导线与磁场垂直时，在时间Δt内安培力的冲量FΔt=IBLΔt=BLΔq，Δq是通过导体截面的电荷量，在含容电路中解答电荷量问题十分方便，无论导体棒是否存在电阻，均是求解电荷量的一种有效方法。

【教学策略一】改变条件结构，相似情境不同问题，方法归一

题型一以电磁推动加喷气推动的火箭发射问题为例

【2016年4月卷】如图4所示，竖直固定在绝缘底座上的两根长直光滑导轨，间距为L，导轨间加有垂直导轨平面向里的匀强磁场B，绝缘火箭支撑在导轨间，总质量为m，其中燃料质量为m′，燃料室中的金属棒EF电阻为R，并通过电刷与电阻可忽略的导轨良好接触。

图4

引燃火箭下方的推进剂，迅速推动刚性金属棒CD(电阻可忽略且和导轨接触良好)向上运动，当回路CEFDC面积减少量达到最大值ΔS，用时Δt，此过程激励出强电流，产生电磁推力加速火箭。在Δt时间内，电阻R产生的焦耳热使燃料燃烧形成高温高压气体。当燃烧室下方的可控喷气孔打开后。喷出燃气进一步加速火箭。(1)求回路在Δt时间内感应电动势的平均值及通过金属棒EF的电荷量，并判断金属棒EF中的感应电流方向；(2)经Δt时间火箭恰好脱离导轨。求火箭脱离时的速度v0(不计空气阻力)；(3)略。

【教学策略二】改变条件情境，不同条件相似问题，方法整合

题型二以含容电路下导体棒的运动为例

【2013年新课标】如图5，两条平行导轨所在平面与水平地面的夹角为θ，间距为L。导轨上端接有一平行板电容器，电容为C。导轨处于匀强磁场中，磁感应强度大小为B，方向垂直于导轨平面。在导轨上放置一质量为m的金属棒，棒可沿导轨下滑，且在下滑过程中保持与导轨垂直并良好接触。已知金属棒与导轨之间的动摩擦因数为μ，重力加速度大小为g。忽略所有电阻。让金属棒从导轨上端由静止开始下滑，求：金属棒的速度大小随时间变化的关系。

图5

依据上述策略，围绕“导体棒(框)”在电磁感应中的作用组织教学，综合研究导体棒(单棒、多棒等)、导体框(圆形、矩形等)、含容电路、含电感电路进出磁场的感应过程；运用动量定理、动量守恒定律、安培力作用下的功能关系、牛顿第二定律、微元法等知识解决不同情境下的不同问题；通过变式的教学策略，使学生将某一问题的解决方法用于其他相似问题，形成相应解决问题的科学思维。

三、总结