例析高考试题中平衡常数的求法

湖北 邢泰宇 徐文军

化学平衡常数是表征气相平衡、溶解平衡、电离平衡、水解平衡等平衡体系限度的关键参数，对研究物质在可逆反应中的行为起着重要作用。2018年普通高等学校招生全国统一考试大纲的说明(理科)关于平衡常数有如下描述：“掌握化学平衡的特征，了解化学平衡常数(K)的含义，能利用化学平衡常数进行相关计算”；与2016年“考试说明”相比，“了解弱电解质在水溶液中的电离平衡”改为“理解弱电解质在水中的电离平衡，能利用电离平衡常数进行相关计算”，“了解难溶电解质的沉淀溶解平衡，了解溶度积的含义及其表达式，能进行相关的计算”改为“了解难溶电解质的沉淀溶解平衡。理解溶度积(Ksp)的含义，能进行相关的计算”，这些表述或改动强化了平衡常数计算问题，凸显了通过化学计算定量地说明化学问题。下面以有关平衡常数的高考试题为例，谈谈平衡常数的求算方法。

一、定义式法

【试题分析】CO2的转化率是50%，即转化了 0.25 mol·L-1，根据平衡三段法得：

起始浓度(mol·L-1) 1 0.5 0 0

转化浓度(mol·L-1) 0.25 0.25 0.5 0.5

平衡浓度(mol·L-1) 0.75 0.25 0.5 0.5

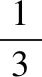
【策略技巧】根据平衡三段法求出各物质平衡浓度，直接代入平衡常数定义式直接求算即可。

二、定义式迁移法

【例2】(2018·全国卷Ⅰ·28节选)F．Daniels等曾利用测压法在刚性反应器中研究了25℃时N2O5(g)的分解反应：

2N2O4(g)

其中NO2二聚为N2O4的反应可以迅速达到平衡。体系的总压强p随时间t的变化如下表所示[t=∞时，N2O5(g)完全分解]：

t/min040801602601 3001 700∞p/kPa35.840.342.545.949.261.262.363.1

【试题分析】N2O5完全分解生成N2O4和O2，起始pN2O5=35.8 kPa，其完全分解时pN2O4=35.8 kPa，pO2=17.9 kPa，设平衡时N2O4转化了x，

平衡(kPa) 35.8-x2x

【参考答案】13.4

【策略技巧】平衡分压式平衡常数(Kp)由浓度式平衡常数(Kc)迁移而来，可先根据三段式求出各物质的平衡分压，再用其代替平衡浓度计算即可。

2014年全国卷Ⅰ、2015年四川卷中也出现过分压式平衡常数(Kp)的计算。

三、特殊点法

1.图象中的交叉点

B．lg[K2(H2A)]=—4.2 ……

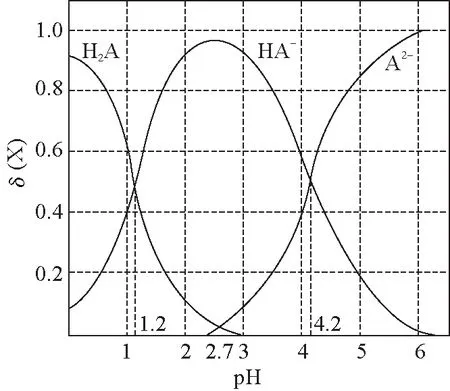
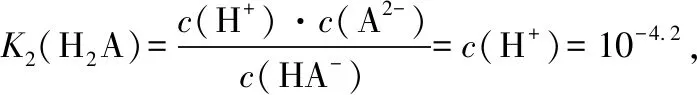
【参考答案】略

【策略技巧】在微粒浓度或物质的量或含量等随pH或时间等变化的图象中，两种微粒的交叉点往往是计算平衡常数的首选点。交叉点时两种微粒浓度相等，平衡常数公式中该两种微粒数值抵消，简化了计算。

2014年浙江卷、2017年江苏卷中也出现过用交叉点来计算平衡常数。

2.图象中有确定坐标值的点

【例4】(2017·全国卷Ⅰ)常温下将NaOH溶液滴加到己二酸(H2X)溶液中，混合溶液的pH与离子浓度变化的关系如图所示。下列叙述错误的是(B、C、D选项省略)

A．Ka2(H2X)的数量级为10-6……

【参考答案】略

【策略技巧】在微粒浓度或物质的量或含量等随pH或时间等变化的图象中，若某点(如起点、交叉点等)有确定的坐标值，可以用该点数据来计算相关平衡常数。

2016年全国卷Ⅰ、2017年全国卷Ⅲ、2018年全国卷Ⅲ中也出现过用特定坐标点的方法来计算平衡常数的试题。

3.速率方程中平衡点

①平衡常数K343K=________(保留2位小数)。

【试题分析】①由图示温度越高反应越快，达到平衡用时就越少，所以a点所在的曲线代表343 K的反应。从图中可以读出，平衡以后反应转化率为22%。设初始加入的SiHCl3的浓度为1 mol/L，则：

起始浓度(mol·L-1) 1 0 0

转化浓度(mol·L-1) 0.22 0.11 0.11

平衡浓度(mol·L-1) 0.78 0.11 0.11

起始浓度(mol·L-1) 1 0 0

起始浓度(mol·L-1) 0.2 0.1 0.1

平衡浓度(mol·L-1) 0.8 0.1 0.1

【参考答案】0.02 1.3

2015年全国卷Ⅰ、2016年海南卷、2017年江苏卷中都曾出现过利用速率方程求算平衡常数的试题。

四、守恒法

【例6】(2012·山东卷)25℃时，将amol NH4NO3溶于水，向该溶液滴加bL氨水后溶液呈中性，则所滴加氨水的浓度为________mol/L(NH3·H2O的电离平衡常数取Kb=2×10-5mol/L)。

【策略技巧】对于电离平衡或水解平衡常数，若不方便建立平衡三段式计算，可先根据溶液中的电荷守恒、物料守恒等关系找出各微粒的浓度，再代入平衡常数的定义式中计算。

五、“盖斯定律”法

【参考答案】8.7×10-7

【策略技巧】已知多个相关反应的平衡常数，可用“盖斯定律”法将多个方程式相加或相减，得到目标方程式，对应方程式的K是相乘或相除的关系，若目标方程式系数是已知方程式的n倍，则目标方程式K是已知方程式K的n次方。

六、比值等量法

【参考答案】20

【策略技巧】将目标方程式的平衡常数表达式分子、分母同时乘以c(H+)或c(OH-)等与已知方程式相关的量时，比值保持不变，如例题8，该方法通常用于多个相关方程式之间K值求算，与例题7使用“盖斯定律”法实质是一样的，例题8也可以用“盖斯定律”法计算平衡常数。